动力学模态分解方法重构及预测流场误差分析
2021-03-16孙国勇董加新赵志高王玉川
孙国勇, 董加新, 赵志高, 王玉川
(1. 西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100; 2. 武汉大学 水资源与水电工程国家重点实验室, 湖北 武汉 430072)
理论模型方程可以准确、完整地描述一个系统的动态特性.但是,当模型方程不能确定或不完善时,就需要使用数据本身解释系统.近年来,为描述系统动力学特性,对系统数据矩阵降维处理并建立其线性近似动力学模型已被证明是一种行之有效的方法[1].动力学模态分解(dynamic mode decomposition, DMD)是一种数据驱动算法,无需控制方程,直接从试验测量或数值模拟流场数据中提取动力学信息,用于分析复杂非定常流动主要特征或建立低阶流场动力学模型,从而实现预测和控制给定流场.这种方法的最大优势是分解所得模态具有单一频率和增长/衰减率[2],因此在分析和研究周期性流动问题上更具优势.目前,已被应用到许多非定常流场分析中,如方腔流动[3]、文丘里管空化流动[4]和混流泵叶顶泄落涡[5]等.但是目前基于DMD对流场进行重构、预测误差变化的研究还有待深入,这也是DMD应用于流体工程中的核心问题.
圆柱绕流产生卡门涡诱导涡激振荡是流体工程中常见的非定常流动现象,如海洋细长柔性立管[6]、高空悬索桥[7]以及超高层建筑[8]等,涡激共振会导致微动磨损、碰撞损坏和材料疲劳等.2020年5月广东省虎门悬索大桥产生异常抖动正是涡激共振所导致[9].而动力学模态分解分析能够获取各阶模态的单一频率所对应的流场相干结构和模态能量,将其与结构固有频率进行对比分析,从而为有效抑制涡激共振提供指导.另一方面,作为流体力学经典问题,研究人员对圆柱绕流流动规律已经有较为深刻的认识,因此,经常用作流场分析方法的应用对象,来验证方法可行性和可靠性.采用仿真计算可模拟卡门涡形成、发展(非线性变化)和稳定脱落(周期性变化)过程,已成为典型的验证数据分析方法.近年来,叶坤等[10]以圆柱绕流为例,采用DMD方法提取模态,验证了方法的准确性和可行性.但是,上述研究都没有进行基于DMD方法流场重构和预测的误差分析.
笔者以雷诺数Re=80的圆柱绕流卡门涡街形成的非线性发展过程和周期性脱落过程为例,研究非定常流场的动力学模态分解、重构及预测,重点分析重构和预测的误差变化发展规律.首先,采用数值模拟方法分析Re=80的圆柱绕流卡门涡形成、发展和稳定脱落的非定常流场过程;其次,通过动力学模态分解技术对流场进行降维分解处理,得到流场各阶DMD降维模型,进而利用降维模型重构和预测圆柱绕流的非定常流场;最后,定量分析不同阶段不同样本DMD方法重构和预测二维圆柱绕流非定常流场的误差发展情况.
1 数值模拟
1.1 圆柱绕流数值模拟
计算区域如图1所示,圆柱直径为特征长度D,计算模型区域选为25.0D×10.0D,计算域网格采用结构化网格,中心圆柱采用O型网格进行加密.网格总节点数为46 012个.圆柱表面为无滑移边界条件,上下侧采用对称边界,入口条件设置为速度入口,出口条件为充分发展的自由出流边界条件.

图1 计算域示意图
采用SIMPLE算法进行数值模拟,时间步长Δt=0.5 s.进口来流条件为Re=80(进口流速v=0.011 69 m·s-1),选用层流模型,介质为空气,运动黏度为1.460 7×10-5m2·s-1,控制收敛精度为10-4,计算总步数设置为3 600 步,即模拟1 800 s的圆柱绕流非定常流场流动过程.
1.2 数值模拟结果的验证
数值模拟的卡门涡形成过程的升力系数Cl时域图如图2所示.根据升力曲线的变化特征,将卡门涡的发展过程分为3个阶段(见图2中Ⅰ、Ⅱ、Ⅲ).第Ⅱ和第Ⅲ阶段升力系数FFT变换后的主要频率及幅值如表1所示.

图2 升力系数时域图
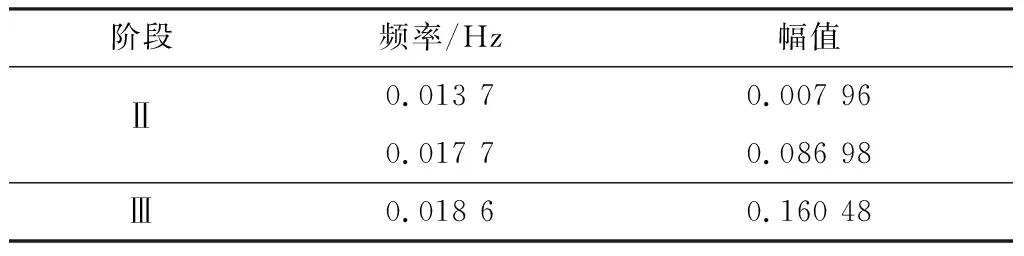
表1 升力系数主要频率及幅值
斯特劳哈尔数为
(1)
式中:fo为旋涡脱落频率, Hz;v为自由来流速度, m·s-1.
文献[11]拟合的斯特劳哈尔数为
(2)
从表1可以看出:第Ⅲ阶段(卡门涡稳定脱落)升力系数主频为0.018 6 Hz,由式(1)可得斯特劳哈尔数Sr为0.159 1,由式(2)计算的结果为0.154 7,两者误差为2.8%,说明数值计算准确捕捉到了卡门涡脱落的动态过程.同时,数值计算模拟的卡门涡非线性形成过程,与文献[10,12]的计算结果一致,进一步验证了计算的准确性.
1.3 卡门涡街发展过程
由图2可知,卡门涡形成过程可以分为3个阶段,各个阶段涡形态分别如图3-5所示.第Ⅰ阶段(图3),边界层开始分离,在圆柱后面形成对称漩涡并逐渐向下游发展形成细长尾迹,直至出口,这一阶段,对称的尾涡虽然生长发展,但过程缓慢,始终呈现对称状态,因此升力系数波动很微弱;第Ⅱ阶段(图4),细长尾涡变得不稳定,开始沿垂直方向摆动,随摆动幅度增大,升力系数也逐渐增大,直至发展成为稳定的卡门涡,此阶段是非线性发展过程;第Ⅲ阶段(图5),卡门涡处于稳定周期性脱落过程,升力系数表现为稳定周期性波动.
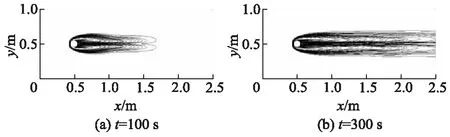
图3 卡门涡形成阶段

图4 卡门涡发展阶段

图5 卡门涡稳定脱落阶段(t=1 300 s)
2 动力学模态分解方法
数值计算后,可得N个时刻流场快照序列矩阵X=[x1x2…xN],其中任意相邻2个流场数据快照xi的时间间隔Δt很小,则向量xi+1和xi成线性映射关系,即
xi+1=Axi,
(3)
式中:A为高维矩阵.
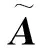
(4)
(5)
(6)
式中:U为左奇异矩阵;Σ为奇异值对角矩阵;V*、U*分别为V、U的复共轭转置矩阵.
(7)
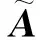
将特征值λi对数化,可得第i个模态对应增长/衰减率σi和包含模态频率信息的相速度ωi,即
(8)
频率为
(9)
通过特征向量,构建DMD动态模型:
Φ=UW.
(10)
最后进行流场数据重构及预测,实现任意时刻流场重构预测的方程式为

(11)
式中:b为模态幅值[13]bi构成的向量;K为模态数.
(12)
依据模态能量[14]标准提取主要模态,即
(13)
式中:I为模态能量;‖·‖F为Frobenius范数.
为检验重构以及预测流场的准确性,定义相对误差函数为
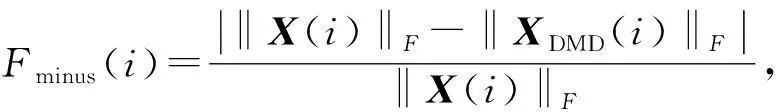
(14)
式中:X(i)为流场第i时刻流场快照;XDMD(i)为DMD重构预测流场第i时刻流场快照.
3 DMD结果及误差变化分析
选取第Ⅱ、Ⅲ阶段典型流场数据,研究DMD方法对非线性和周期性流场重构和预测的误差变化情况及其与样本关系.从第Ⅱ阶段提取3组数据样本、第Ⅲ阶段提取1组数据样本用以研究各阶段流场结构的主要特征,4组数据样本如下: ① 300~450 s数据快照(见图2中①);② 450~600 s数据快照(见图2中②);③ 600~750 s数据快照(见图2中③);④ 1 100~1 250 s数据快照(见图2中④).
动态模态分解获得的特征值λi实部(σi)为正,对应模态系数发散;σi为负,对应模态系数收敛;σi为0,对应模态系数稳定;虚部ωi表示包含模态频率信息的相速度.在进行稳定性判断时,同样将λi置于复平面单位圆上判断,单位圆内,模态收敛;单位圆外,模态发散;单位圆上,则为稳定模态.
3.1 卡门涡发展阶段
3.1.1 稳定性分析
利用第②组数据样本做DMD处理,得到特征值分布.发展阶段模态特征值及对数化特征值实虚部关系如图6所示.

图6 发展阶段模态特征值及对数化特征值实虚部关系图
特征值以共轭复数形式成对出现的模态,称共轭模态,实际上是1个模态(具有相同的动力学特性).同时绝大多数模态位于单位圆内,且非常接近单位圆,说明发展阶段大多数模态均为衰减较慢的弱稳定模态;极少数模态位于单位圆上,说明发展阶段存在极少数极限稳定的周期性循环模态,从图6b可以看出,存在部分模态σi>0,说明模态发散.将模态能量按由大到小排序,因共轭模态实际为1个模态,故只取其中1个模态进行分析,定义前i阶模态所占能量比和第i阶模态所占能量比分别为
N=1,2,…,R,
(15)
(16)
式中:R为去除共轭模态中的1个模态后剩余模态的总数.
前i阶模态所占能量比与第i阶模态所占能量比如图7所示,发展阶段,提取的前6阶主要模态所占能量比大于96.00%,动力学参数如表2所示.1阶模态的σ1与ω1均为0,这是静态模态,表示样本时间段内流场平均特性,整体上不会随着时间而变化,其能量占比为92.69%.其中2、3、5阶模态的σ为正,但数值很小,对应发散缓慢弱稳定模态.而4、6阶模态σ为负,数值也很小,对应衰减缓慢弱稳定.同时应用DMD方法获取2阶模态频率0.017 7 Hz与FFT得到的第Ⅱ阶段主频0.017 7 Hz相同,这说明DMD方法可准确提取主频模态.由于本阶段各模态发散、收敛掺杂,所以表现为发展阶段流场的非线性发展过程.

图7 第②组数据前i阶模态及第i阶模态所占能量比

表2 发展阶段提取的DMD模态动力学特性参数
第②组数据模态能量分别与增长/衰减率σi及Sr的关系如图8所示.

图8 第②组数据模态能量分别与增长/衰减率及Sr的关系
从图8可以看出,高能量模态全部分布在低增长/衰减率和低频的状态下,这说明对流场起主要作用的是低频和低增长/衰减率模态,且大尺度相干结构变化相较于小尺度相干结构变化慢.
对第①组和第③组数据做同样的DMD处理,发现模态特征值分布和动力学信息与第②组相比,规律一致,但由于截取数组时间段不同,提取流场动态信息也不完全相同.
3.1.2 非线性变化流场重构与预测误差变化
在此非线性流动阶段,选取第①、②、③组流场大数据样本进行重构预测研究,基于这3组数据用式(11)进行流场重构和预测,并利用式(14)分析重构及预测流场误差,结果如图9所示.

图9 3组数据重构预测与实际流场的相对误差
从图9可以看出:对于重构流场,DMD方法均可对提取的3组数据进行准确重构,误差量级仅为10-13;对于预测流场,误差较重构流场阶跃增大,但是在近似一定时间范围内(近似与样本时间相同),亦可较为准确地预测流场发展,误差为10-3~10-5.在圆柱绕流非线性发展阶段,第①、②组数据可以较为准确预测其后150 s左右的流场,之后流场会随时间增长,差值呈指数增大;第③组数据由于接近周期性波动的第Ⅲ阶段,预测流场误差随时间增长也变大,但变大速度缓慢,且有逐渐趋于平缓的趋势,预测到1 000 s时,误差接近10-3.这说明第③组数据DMD近似系统矩阵已基本包含卡门涡稳定脱落阶段周期性流场动力学信息.由上述分析可知,根据不同样本数据近似得到的系统矩阵所包含的动力学信息不完全一致.因而,DMD对非线性变化流场的预测能力有限.
第③组数据预测和仿真得到的1 000 s流场速度云图如图10所示.

图10 第③组数据预测与仿真得到的1 000 s流场速度云图
从图10可以看出:利用第③组数据可以预测1 000 s(卡门涡发展阶段结束时间点)流场的主要相干结构和流场卡门涡主要形态,验证了上述误差分析的准确性;发展阶段为非线性发展过程,因此预测流场速度云图边界没有仿真计算的流场光滑.
3.2 卡门涡稳定脱落阶段
3.2.1 稳定性分析
第④组数据进行DMD计算得到的稳定脱落阶段模态特征值及对数化特征值实虚部关系如图11所示.

图11 稳定脱落阶段模态特征值及对数化特征值实虚部关系图
从图11a可以看出:稳定脱落阶段,有部分模态位于单位圆上,对应稳定循环周期性模态,部分模态处于单位圆的内部但非常接近单位圆,对应衰减缓慢弱稳定周期性模态,少部分模态位于距离单位圆较远的内部,对应衰减较快的收敛模态.结合图11b,可准确得出本阶段无发散模态.综上可知,稳定脱落阶段流场体现为周期性稳定的特性.
同理,通过式(15)、(16)可得稳定脱落阶段前i阶模态所占能量比与第i阶模态所占能量比,如图12所示,1阶模态占总能量的92.32%,前6阶模态,所占能量比大于97.00%,本阶段提取对流场起主要作用的前6阶主要模态进行研究.结合表3,可以定量看出前6阶模态详细动力学参数,1阶模态σ与ω均为0,为静态模态,不做考虑.其余能量占比较大的模态均表现为σ=0,对应着稳定周期性循环模态,进一步说明了本阶段流场表现为稳定周期性循环状态.应用DMD方法提取的2阶模态频率为0.018 9 Hz,与FFT分析的主频0.018 6 Hz误差为1.6%,说明此方法准确地提取了绕流流动的动力学信息.

图12 稳定脱落阶段前i阶模态及第i阶模态所占能量比
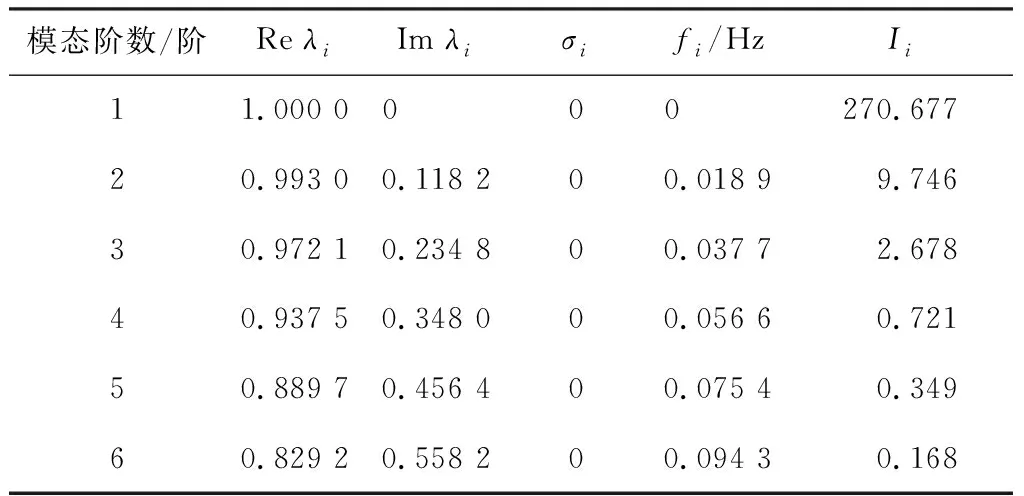
表3 稳定脱落阶段提取的DMD模态动力学特性参数
稳定脱落阶段模态能量与增长/衰减率及Sr的关系如图13所示,高能量模态都处于低频和低增长/衰减率状态,高频模态所具有的能量相对很小,对流场影响不大.这进一步表明大尺度的相干结构较小尺度的相干结构变化较慢.

图13 稳定脱落阶段模态能量分别与增长/衰减率及Sr的关系图
模态向量虚部和实部刻画的流场相干结构形态相似,仅存在一定相位差异[12],前6阶模态刻画的流场相干结构云图如图14所示,vf为流速.
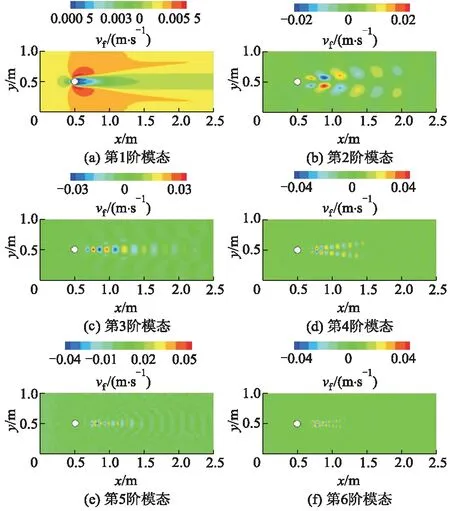
图14 稳定脱落阶段前6阶模态云图
从图14可以看出:第1阶模态为静态模态(即平均流场),它不随时间变化而改变,代表流场的主要特性;第2阶模态捕获了明显的漩涡交替脱落现象,其频率与升力曲线的主要频率相同,是卡门涡的主导相干结构;随着模态阶数增高,其所含能量逐渐减小,相干结构尺寸逐渐减小,脱落频率逐渐增大,漩涡数量也在增多.
3.2.2 周期性流场重构与预测误差变化
稳定脱落阶段流场为周期性流动,选择第④组数据对本阶段流场进行流场重构和预测,并分析重构及预测流场误差,结果如图15所示.

图15 第④组数据重构预测与实际流场的相对误差
从图15可以看出: DMD方法能够准确重构截取数据样本的流场,误差小于10-13,对于预测流场误差同样存在阶跃增大,但误差随时间变化基本稳定在10-4.
第④组数据预测与仿真得到的1 800 s流场速度云图如图16所示,预测流场准确捕捉到了稳定脱落阶段与仿真计算流场较为相似的流场主要相干结构.
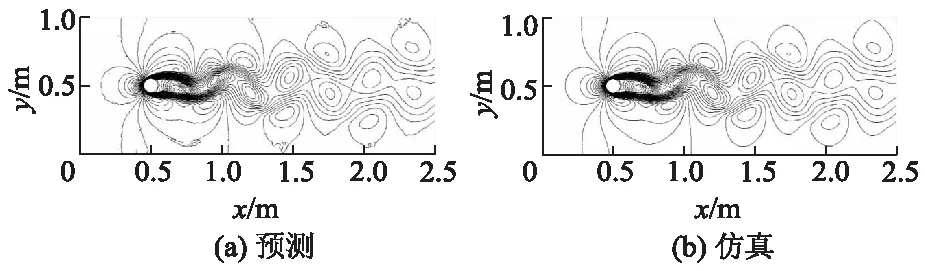
图16 第④组数据预测与仿真得到的1 800 s流场速度云图
4 结 论
1) DMD方法可以分解出圆柱绕流非定常流场中各单一频率对应的相干结构和动力学信息,捕获主频下流场相干结构的形状及发生位置.低频、低增长/衰减率、对应的大尺度相干结构具有较大能量,对流场起决定作用,而高频,高增长/衰减率、小尺度相干结构模态具有较小能量,对整个流场影响很小.
2) DMD方法可以准确重构流场,非线性变化和周期性变化重构流场的误差均小于10-10,与所选数据样本无关;预测流场的误差相比重构流场会出现阶跃增长,但非线性流场在样本时间内,预测误差小于10-3,预测流场能够表现出原流场的流动结构;超出样本时间,预测流场误差急剧增长,且无法实现对流场的精准预测;而对于周期流场的预测误差变化稳定在10-4,可实现任意时刻流场预测.
