基于发电机运行实际的电力系统日前动态无功优化研究

陆彬，高山，李德胜

基于发电机运行实际的电力系统日前动态无功优化研究

陆彬1，高山2*，李德胜1

（1．万帮数字能源股份有限公司，江苏省 常州市 213164；2．东南大学电气工程学院，江苏省 南京市 210096）

为了解决日前动态无功优化中发电机安全运行极限以及控制设备动作次数约束取值的电力系统调度实际问题，根据发电机运行的极限输出范围，把发电机运行的区域划分为3个区，并建立分段PQ数学模型，将日前全天负荷分为24个时段，并对有载调压变压器和并联电容器组联动次数加以限制，建立完整的非线性混合整数动态无功优化模型。仿真结果表明：尤其在发电机进相运行时，所提出数学模型能有效调节发电机的出力，符合机组运行的实际状况；提高控制设备动作次数可减少全网有功功率损耗，但同时频繁的操作会大大提高设备的故障概率，有必要在网损可信接受的范围内寻找合适的联动次数约束值，节约电网实际运行的综合成本，保障电网经济、安全运行。

动态无功优化；发电机安全运行极限；内点法；电力系统调度

0 引言

虽然日前静态无功优化[1]能使每个独立时段的目标值达到最优，但离散调控设备的动作次数失去了各时段的关联性，频繁操作变压器分接头或投切电容器会大幅降低设备的使用寿命，增大电网的隐患概率。

日前动态无功优化是根据未来一天负荷预测情况，提前统筹各时段下控制设备的操作，最终实现全天的潮流最优。变压器分接头或投切电容器的次数作为全局约束，把各设备全天联动约束次数合理地分配到每个时段，并且使全天的有功网损最小，这一工作使本已复杂的无功优化计算更加难以求解。

文献[2]根据冬、夏季节负荷特性，人为设置各时段控制设备的最大动作次数。这种方法虽然在一定程度上降低了控制设备的动作次数，但是人为设置策略的误差很大，无功优化性不强。

文献[3]把动作次数折算成经济成本，当某设备动作次数达到上限时，就把该设备的调节代价退出目标函数，这种做法失去了动态无功优化的求解意义。

另外，文献[4-7]在对动态无功优化理论研究时注重算法的选择，尤其是智能算法的兴起，但都忽视对电网约束条件的实际考量，比如发电机组的安全运行极限范围。这类研究计算的数据要么没有充分利用发电机组的进相、迟相调节能力，增加了无功调节设备的动作次数；要么超过发电机极限安全运行范围，理论研究和电网的实际运行状态相脱节，给调度员带来误判的风险。

随着电网规模的大幅增大，优化算法的寻优可靠性、快速性、精准性是响应电网调度的重要考量因素，目前求解无功优化的算法很多[8-12]，但都难以满足上述要求。

本文以高效实施电网调度为目的，将罚函数正弦化处理，快速精确实现离散化；根据发电机的实际运行情况，建立离散控制变量的联动次数全局约束和发电机极限安全运行约束，以全天总网损最小作为目标函数，采用内点算法快速计算日前24h动态无功优化。

1 离散无功优化

1.1 非线性混合整数无功优化建模

离散无功优化在数学上表现为典型的非线性混合整数优化问题，常采用非线性原对偶内点法与惩罚函数相结合的方法，表示如下：

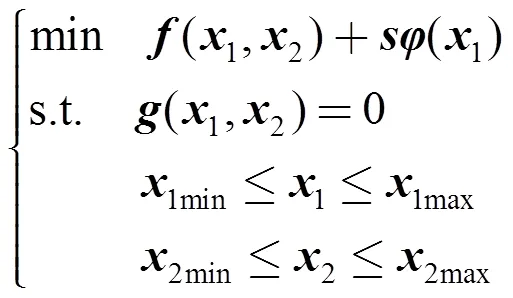
式中：离散变量1=(CT,BT)T，其中包括并联电容器的无功出力列向量C和有载调压变压器变比列向量B，1∈R(p)；连续变量2=(GT，1，⋯，θ-1，GT，T)T，它是由发电机有功出力列向量G、节点电压相角θ(不包括平衡节点)、发电机无功出力列向量G以及节点电压幅值列向量构成，2∈R(q)；1max、1min和2max、2min分别表示约束变量1和2的上、下限；为离散惩罚因子组成的行向量；(∙)为各离散变量构成惩罚函数列向量；(∙)=0为节点功率平衡方程组；(∙)为全网有功功率损耗；(∙)可表示为

=1,2,…,(2)

式中：P、Q为节点的注入有功功率和无功功率；U、U为节点的电压幅值；G、B分别为节点导纳矩阵元素Y的实部和虚部；θ为支路两端电压相角差。

(∙)可表示为

1.2 构造离散变量罚函数

内点法的思路是使迭代点接近边界时其目标函数值迅速增大，从而保证迭代点均为可行域的内点。定义某个离散变量计算值1i(b)邻域(1i(j))为如下区间：

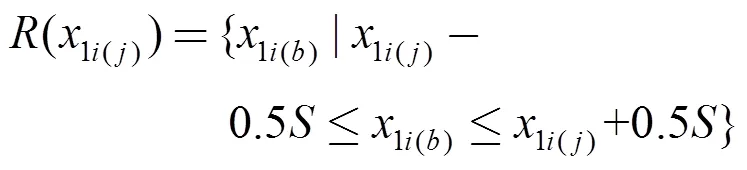
式中：为离散变量1i的分级步长；1i(j)为离散变量取值点。

常规无功优化算法中罚函数(∙)通常使用正曲率二次罚函数：

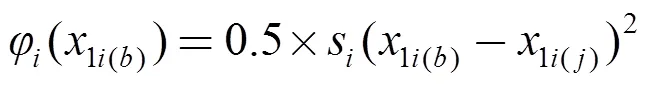
式中s为罚因子。

但在以往内点法计算中发现：对数势垒函数和二次罚函数的组合可能会相互冲突，使结果偏离最优解。所以本文用一种特殊的方式来处理惩罚函数。(∙)由正弦函数处理：

边界处理：当离散变量计算值1i(b)取值为1i(0)或1i(n)时，φ(1i(b))=0；当超出离散取值范围时，φ(1i(b))=100000。

1.3 算例验证

目前智能算法众多，原理类似，以混合粒子群优化算法(particle swarm optimization，PSO)为典型代表，与内嵌二次惩罚项、内嵌SHIN惩罚项的非线性原对偶内点算法进行比较，分别对IEEE 39节点系统进行仿真验证分析。选择该系统的4、7、8、12、15、20、21、23节点为无功补偿设备安装地点，基准功率B=100MV·A。算法比较结果如表1所示。

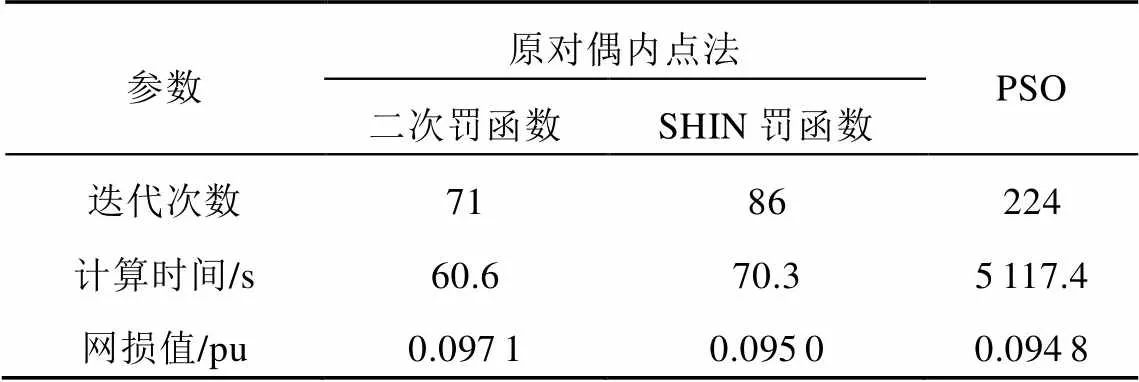
表1 算法比较结果

通过比较发现，在相同的精度条件下，内嵌SHIN罚函数的原对偶内点法和PSO算法结果基本一致，而内嵌二次罚函数的原对偶内点法优化结果偏离最优值较大。PSO算法的迭代次数为224次，计算时间为5117.4s；而内嵌SHIN惩罚函数原对偶内点算法的迭代次数为86次，计算时间为70.3s，可以看出在计算效率上有绝对的优势。

综上，以原对偶内点法作为主体优化算法，通过SHIN惩罚函数能满足无功优化速度快、效率高、结果精确等苛刻要求。

2 考虑发电机运行实际的数学建模

2.1 发电机运行的数学建模

大多数无功优化算法一般都默认发电机运行区间为，如图1所示。以区域作为发电机的运行区域，要么没有充分利用发电机组的进相、迟相调节能力，要么超过发电机极限安全运行范围。

发电机的无功功率供给特性主要受发电机定子绕组温升、励磁绕组温升、原动机功率、静态稳定极限等的约束[13-17]。发电机的无功输出制约了它的有功输出，隐极机安全运行范围如图2 所示。

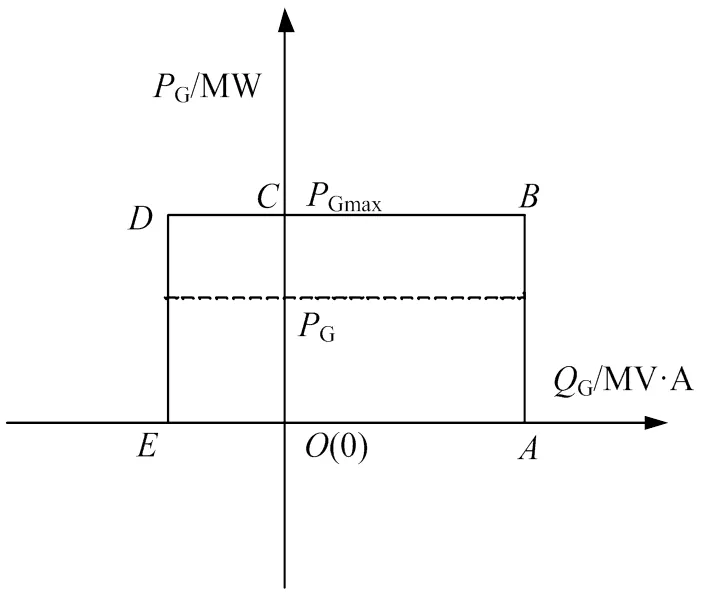
图1 简化模式下发电机安全运行区域

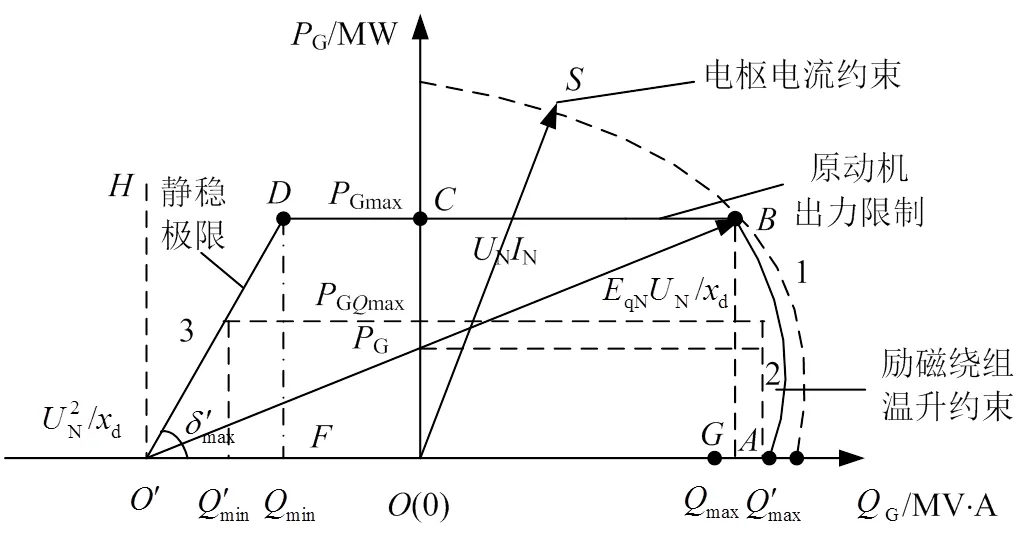
图2 隐极式发电机运行极限图

运行区域说明如下：

1）有功输出确定了无功输出的变化范围。如图2所示，当有功功率为G时，机组端电压决定了无功输出大小，如果机组端电压保持不变，发电机可通过调整励磁电流大小确定所需的无功功率，无功输出范围是[min，max]。此时发电机的电磁功率和输出的有功功率近似保持不变。

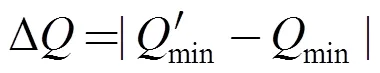
综上所述，在第1节的无功优化模型中需建立隐极机极限安全运行的分段不等式约束(∙)，如下所示：

在′区(Gi<Qmin)，静态稳定极限约束为

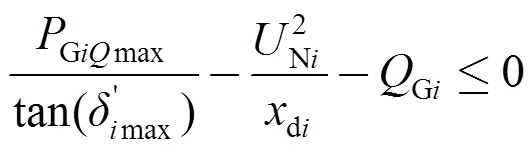
在区(Gi>Gimax)，励磁绕组温升约束为

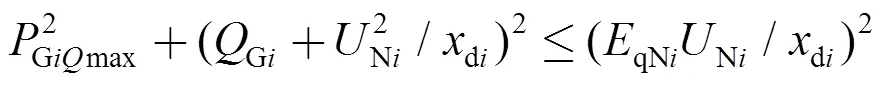
其中：

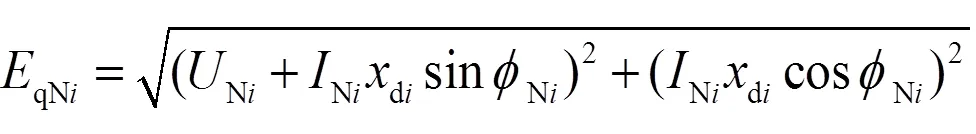
将式(9)代入式(8)得：

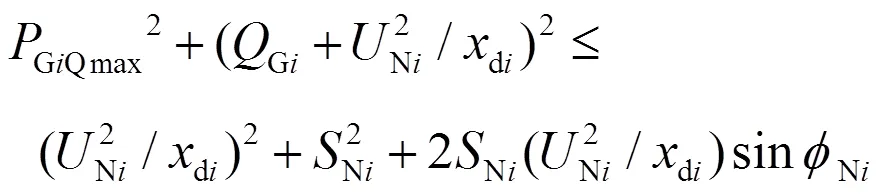
在区发电机无功约束为

Gimin≤Gi≤Gimax，=1，⋯，G(11)

式中：Gi、Gi为节点发电机有功和无功功率；Ni为节点发电机的额定电压值；Ni为节点发电机的额定电流值；di为节点发电机的同步电抗；qNi为节点发电机的激磁电动势；Ni为节点发电机额定功率；Ni为节点发电机额定功率因数角；max、min分别表示上、下限；G为运行在的发电机数；′max一般取80°。

2.2 算例分析

接1.3节算例，2号发电机为平衡机，无功优化结果如表2所示，发电机实际和理论运行对比如图3所示。由表2可看出，当负荷处于波谷时，平衡机出现进相运行，把式(7)—(11)作为约束条件计算后，平衡机发出有功487.74MW且吸收无功为78.06MV·A，如图3中点位置。若不考虑极限安全运行约束条件，平衡机有功输出481.99MW时，进相运行吸收无功143.89MV·A，投射到图3中点位置，大大超过发电机的安全运行极限。

加入发电机极限安全运行约束条件后，发电机进相运行吸收的无功总量减少，未吸收的无功在网络中流动，导致节点电压幅值降低，有功网损比不考虑极限情况下增加了0.008pu，计算结果更符合系统实际运行。

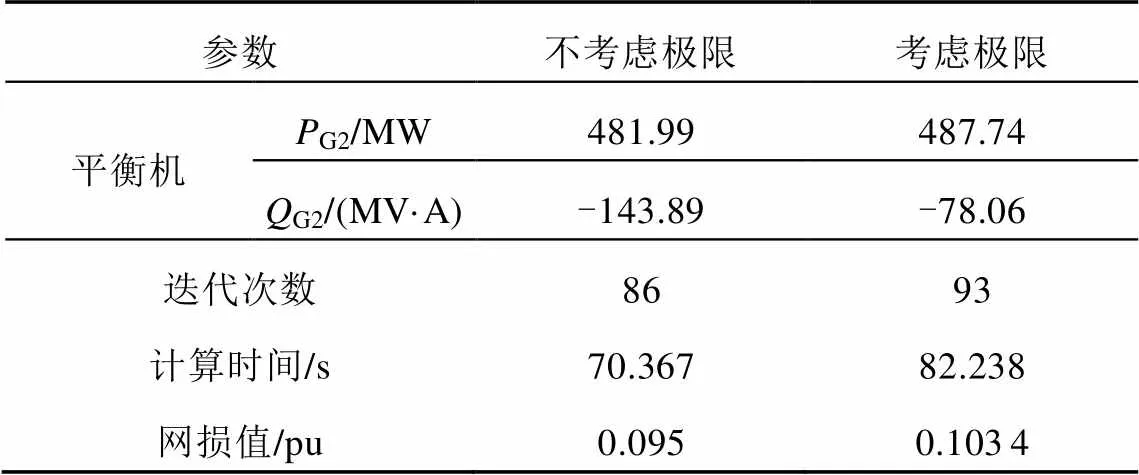
表2 无功优化结果

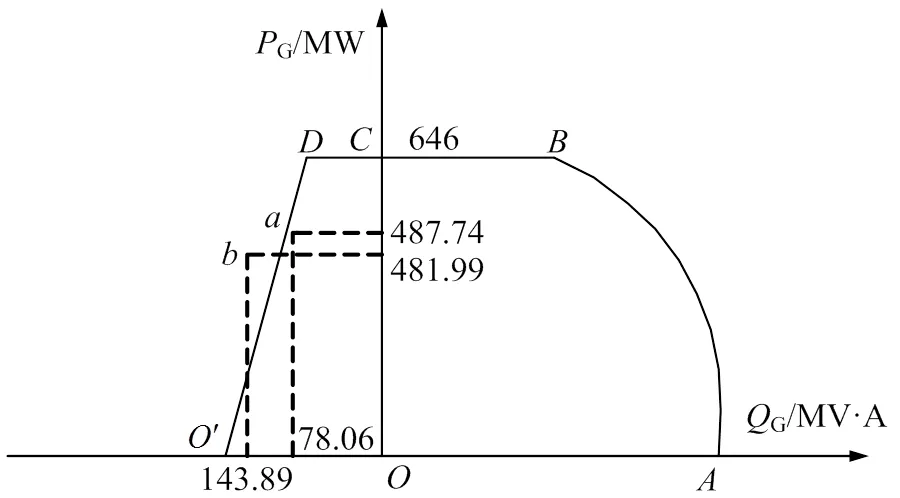
图3 发电机实际和理论运行对比图

3 动态无功优化

动态无功优化问题的核心部分是对各时段下变压器档位变动次数和并联电容器组投切次数准确计数，并应用到全局约束。

3.1 离散控制设备的动作次数约束

按照智能变电站现场运行规程[18]：在变压器有载分接开关操作过程中，应逐级调压，不可连续调2次档位。本文规定：电容器在一次调整中投切的个数即为动作次数，同理，变压器抽头一次调整中连续升或降挡，也认为动了次。

故各离散控制设备全天动作次数可以准确表示为：全天各时段(一般为24段)，相邻每2个时段的离散变量值之差的绝对值求和再除以各自调节步长。

3.2 动态无优化数学模型

在进行日前无功优化时，一般假设全天24个时段下，各时段预测负荷的功率不发生变化，在满足节点功率平衡、电压幅值约束、发电机极限运行约束等约束条件下，使全天整个系统网损最小的动态无功优化模型可以表述为：

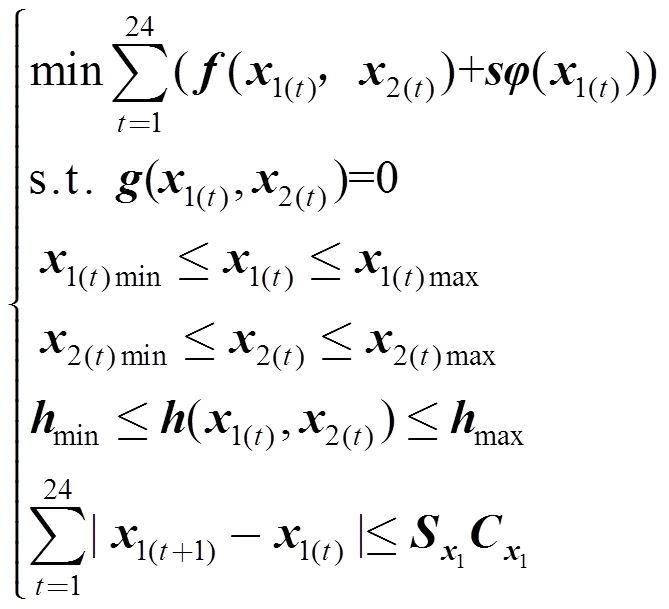
式中C1为控制设备动作次数约束列向量，其元素分别对应于电容器组投切和有载调压变压器分接头的全天最大允许动作次数。

假设给定的电力网络的发电机数有台，有载调压变压器数量有个，并联电容器组数有个，节点数量为个且平衡节点号为。24h动态无功优化的变量扩大为原来的24倍，即24×(2-1+2++)，并且加入发电机极限运行约束，随着系统规模的增大，求解所需的计算时间会急剧增加。

动作次数约束C1是全局不等式约束，其值的设定直接影响算法的计算时间以及收敛状况，如果值设定过小，迭代计算结果较难满足给定的补偿间隙精度条件，如果最大迭代次数仍然不能满足，程序会判断出不能收敛。

4 动态无功算例分析

4.1 算例验证

24h负荷曲线分布如图4所示。算例仍采用39节点系统。根据第2节中的数学模型进行仿真计算，39节点系统从单时段静态无功117个约束变量扩展至24h动态无功2808个约束变量，再加上各变量之间的强耦合联动性，求解规模急剧增大且更为复杂。

理论上对应不同的变压器或者电容器，其所对应的全天最大动作次数应有所不同。为方便起见，且计算结果不影响本文总结的规律，对所有离散控制设备采用同一个动作次数约束值，即C1中的元素都相等。

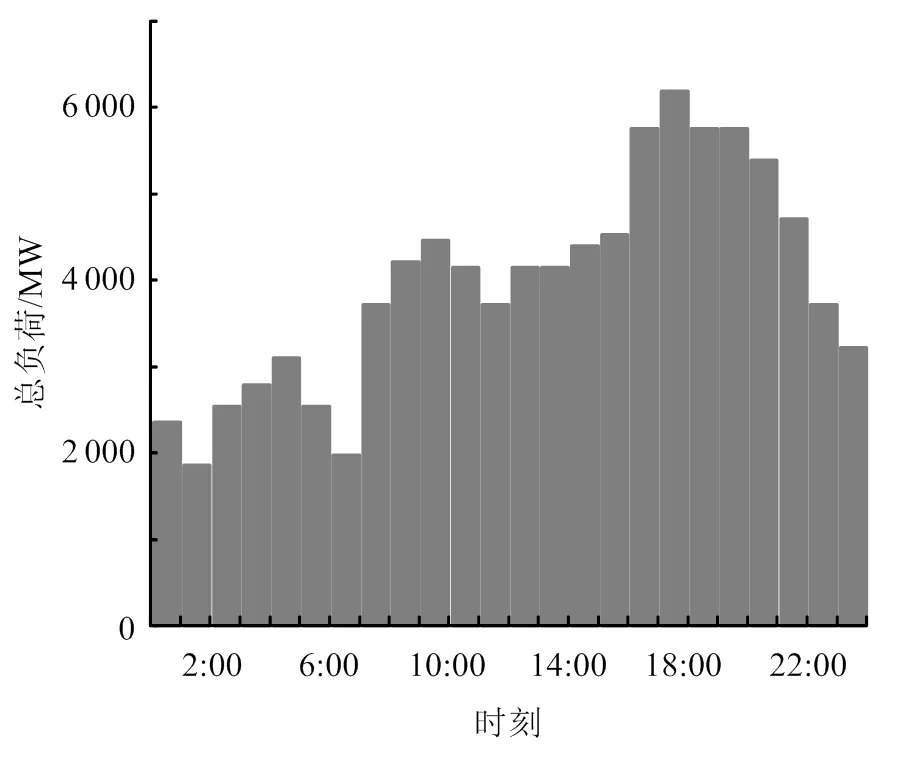
图4 10机39节点日负荷曲线

4.2 动作次数与有功网损

当C1取10、21及静态无功条件时，图5所示分别对应C1的各时段有功网损优化曲线。

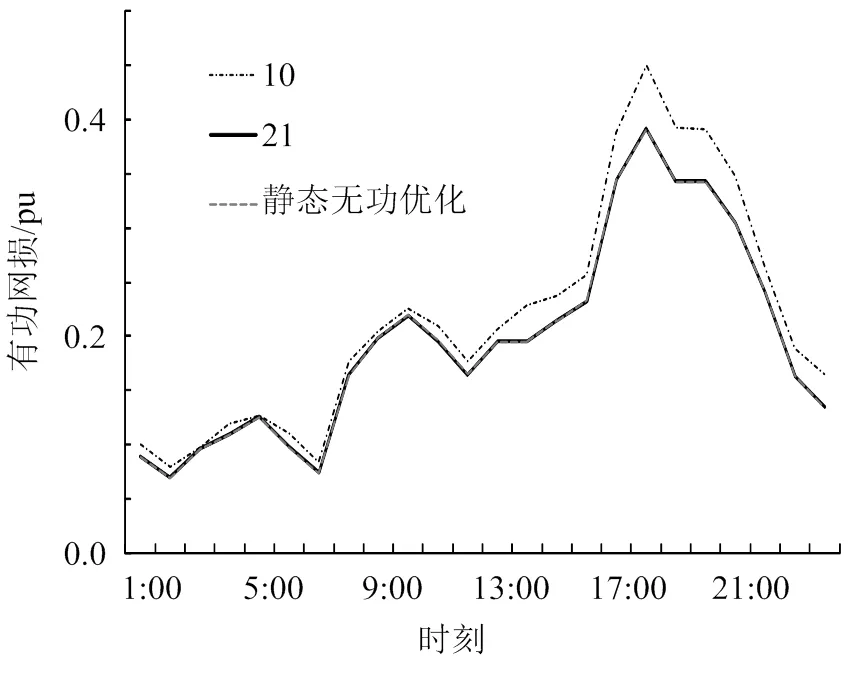
图5 有功网损变化曲线图

从图5可以看出，有功网损的曲线变化趋势与日负荷曲线是一致的。C1取10时的网损曲线在C1取21时和静态无功优化下的网损曲线之上，尤其在负荷高峰时段(下午4点至9点)，更为明显。这是由于C1取值比较苛刻，尤其是在负荷高峰时，强耦合的联动约束使电容器组不能充分投入实现就地无功补偿，导致大部分全网无功优化分配由发电机输出来进行调节，大量的无功在网络中流动，造成了有功功率损耗上升。

当C1取21时，有功网损变化曲线几乎和静态无功优化下的网损曲线重合，这说明21次已经满足离散控制设备的最大动作次数，此时没有大量的无功在网络中流动。

有功网损和计算时间如表3所示，由表3可看出，由于各离散控制变量之间的强耦合联动性，C1取值较低时，对算法的收敛性很大，C1取9及以下时不收敛。C1取10~12时，由于电容器不能充分就地投入，大部分无功优化需求由发电机输出来进行调节，大量无功在电网中传送，网损显著增大。C1取13时，网损下降出现拐点，降幅达6%，C1继续增大，网损变化幅度趋于平缓，故动作次数约束值C1取13时可作为经济安全的无功优化调度策略。

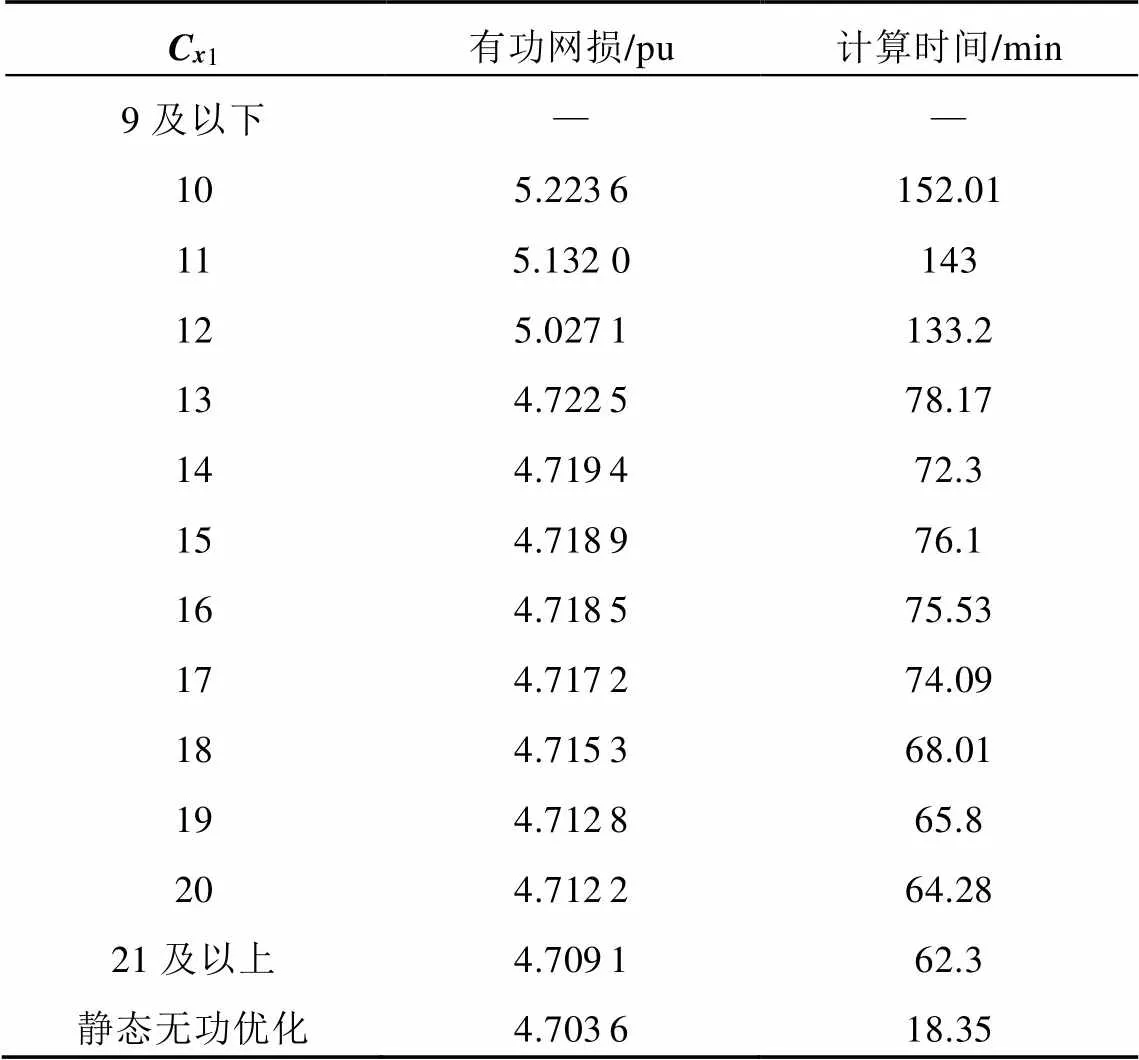
表3 有功网损和计算时间

4.3 动作次数与电容器组无功出力

根据前面阐述，设8号节点有5组电容器组，每组容量为0.07，选取了C1分别为10、13和21时，8号节点电容器组全天各时刻投切值，如图6所示。

图6 8号节点电容器组投切曲线图

从图6可以看出，在C1=10时，4—16时段无功出力维持在0.07，17—22时段无功出力维持在0.14，动作次数累计变化6次，此时电容器组无法响应日负荷变化趋势，尤其是在负荷高峰时，强耦合的联动约束使电容器组不能充分投入实现就地无功补偿，发电机发出无功在网络中流动，造成了有功功率损耗上升。而在C1=13及以上时，电容器组的投切序列不发生变化，且与日负荷的变化趋势一致，这也证明了动作次数约束值C1取13时可作为经济安全的无功优化调度策略。

4.4 变压器分接头动作次数

表4列出了C1分别为10、13、21及静态无功优化算法下，12组变压器全天动作次数统计。

表4 变压器分接头动作次数统计

由表4可知，C1为10次时，联动约束条件十分苛刻，各变压器分接头不能充分调节，导致全网的有功损耗上升。当C1为13时，网损计算值比静态分析增大了约0.41%，但是分接头动作次数比静态优化明显减少46%。

从另一个角度来说，在网损可信范围内，降低分接头动作次数不仅节约了经济成本，而且有效降低了设备频繁操作而导致故障的概率，大大延缓了变压器的使用寿命。综上，在网损可接受范围内，确定适当的C1来平衡有功网损及操作所带来的经济、安全成本。

在本算例中，动作次数约束值C1取13时可作为经济安全的无功优化调度策略。

4.5 变压器低压侧母线电压

电压质量是一项非常重要的指标，尤其是直接面向用户的变压器低压侧电压幅值。图7给出了C1为10、13、21时动态优化及静态优化下变压器T2-30低压侧全天电压幅值变化曲线。

从图7中可以看出，C1取13、21和静态优化时，全天电压幅值曲线均在C1取10的曲线上方。当C1取值比较苛刻时，整个系统偏向无功补偿不足，系统所缺的无功需求只能由发电机来提供，无功功率从发电侧传导到负荷侧，导致系统电压水平降低。

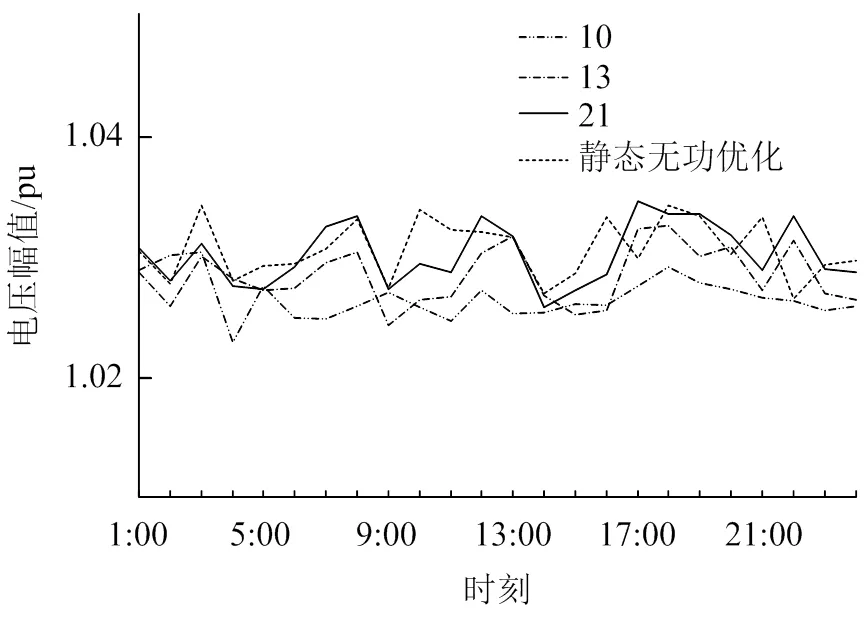
图7 变压器T2-30低压侧母线电压变化曲线

C1取13、21和静态优化时电压波动比C1取10时要剧烈得多，这是因为此时动作次数约束宽裕，变压器分接头动作频繁。

4.6 动作次数与发电机无功出力

平衡的无功出力能直观地反映电网的无功流向。取C1为10、13、21及静态无功优化时，全天24时段平衡机的无功输出曲线如图8所示。

由图8可看出，1—7时段4条曲线几乎重叠在一起，因为此时内负荷水平较低，大多数的电容器组处于全部切除的状态，平衡机处进相运行吸收电网中多余的无功功率，计算结果对C1的取值不敏感。平衡机的无功出力对应于同的C1取值时在负荷高峰时段有明显的差异，当C1取10时，各离散控制设备受到苛刻的约束条件而未能充分投入使用，发电机组须大量发送无功功率来维持电网的功率平衡。

动作次数约束值C1取13、21时与静态无功优化比较，3条曲线几乎重合。尤其在高峰负荷时，电容器组能充分投切实现就地无功补偿，使整个系统无功变化温和，其削峰作用对电网电压稳定具有很大的作用。在本算例中也可以看出，动作次数约束值C1取13时可作为经济安全的无功优化调度策略。

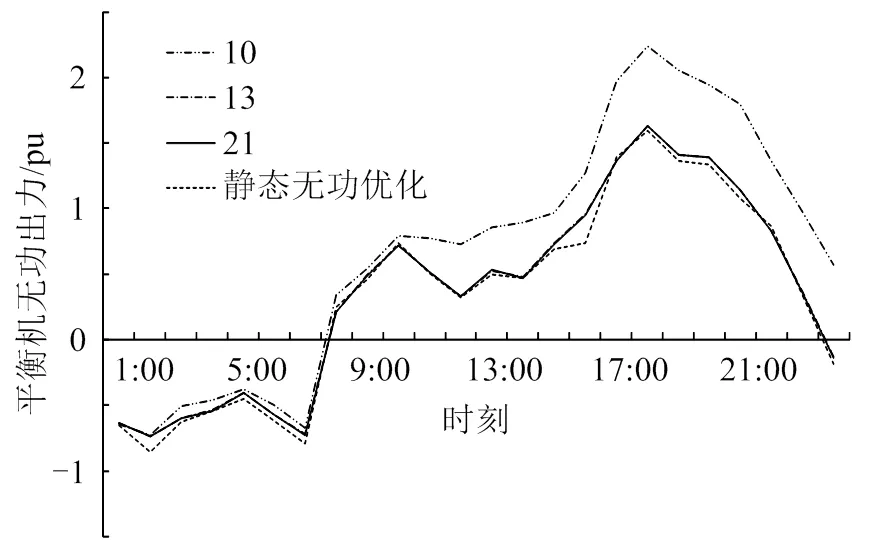
图8 2#发电机全天无功出力变化曲线

5 结论

基于发电机安全运行极限建立24h动态无功优化数学模型，通过原对偶内点法能快速、可靠、精准计算算例中的最优潮流分布。所建模型不仅适用于日前调度计划，也适用于当日实时滚动调度(未来1h调度)；研究了控制设备动作次数约束值与有功网损、电容器组无功出力、变压器分接头调节、变压器低压侧母线电压、电机无功出力的关系。得到以下结论：

1）根据发电机实际运行的极限输出范围，把发电机运行的区域划分为3个区，建立发电机分段离散无功优化数学模型。尤其在发电机进相运行时，有效调节发电机的有功、无功出力符合运行实际，确保了电力系统调度的安全稳定。

2）提高控制设备动作次数可减少全网有功功率损耗，但同时频繁的操作会大大提高设备的故障概率，增加系统安全运行风险。所以有必要在网损可信接受的范围内，减少设备的操作次数，寻找合适的C1，节约电网实际运行的综合成本。在本文算例中，动作次数约束值C1取13时可作为电网经济安全的无功优化调度策略。

[1]王晓文，赵彦辉．电力系统无功优化模型的研究综述[J]．华北水利水电大学学报(自然科学版)，2015，36(2)：63-69．

WANG X W，ZHAO Y H．Summary on reactive power optimization models in electric system[J]．Journal of North China University of Water Resources and Electric Power (Natural Science Edition)，2015，36(2)：63-69．

[2]陈宏文，李爱元，黄旭，等．基于减少设备投切次数的地县一体化AVC控制[J]．湖南电力，2017，37(2)：132-135．

CHEN H W，LI A Y，HUANG X，et al．Prefecture-county AVC control based on reducing equipment action times[J]．Hunan Electric Power，2017，37(2)：132-135．

[3]赖永生，陈燕梅，黄伟．考虑开关动作次数约束的地区供电系统电压无功控制[J]．电能质量管理，2011，9(17)：13-20．

LAI Y S，CHEN Y M，HUANG W．Reactive power control of regional power supply system considering the constraints of switching operations[J]．Electric Energy Quality Management，2011，9(17)：13-20．

[4]孙守鑫，张超，孟庆江，等．减少设备动作次数的无功优化新方法[J]．电力技术，2015，25(4)：68-70．

SUN S X，ZHANG C，MENG Q J，et al．A new reactive power optimization method for reducing the number of operations of equipment[J]．Electric Power，2015，25(4)：68-70．

[5]覃海，姬源，周川梅，等．计及控制设备动作次数约束的三阶段动态无功优化算法[J]．电力自动化设备，2018，38(9)：179-185．

QIN H，JI Y，ZHOU C M，et al．Three-stage dynamic reactive power optimization algorithm considering constraints of control device action times[J]．Electric Power Automation Equipment，2018，38(9)：179-185．

[6]赵晋泉，居俐洁，罗卫华，等．计及分区动态无功储备的无功电压控制模型与方法[J]．电力自动化设备，2015，35(5)：100-105．

ZHAO J Q，JU L J，LUO W H，et al．Reactive voltage control model and method considering partitioned dynamic reactive power reserve[J]．Electric Power Automation Equipment，2015，35(5)：100-105．

[7]葛朝晖，王颖，刘梦怡，等．基于自适应粒子群优化算法的有源配电网多目标动态无功优化[J]．电力系统及其自动化学报，2018，30(11)：44-50．

GE Z H，WANG Y，LIU M Y，et al．Multi-objective dynamic reactive power optimization of active distribution network based on adaptive particle swarm optimization algorithm[J]．Proceedings of the CSU-EPSA，2018，30(11)：44-50．

[8]赖晓文，马晓伟，白杨，等．基于混合整数二阶锥规划的动态无功优化方法[J]．电力系统自动化，2017，41(17)：37-42．

LAI X W，MA X W，BAI Y，et al．Dynamic reactive power optimization method based on mixed integer second-order cone programming[J]．Automation of Electric Power Systems，2017，41(17)：37-42．

[9]徐朝阳，王孝友，徐德贵，等．基于改进粒子群算法的动态无功优化研究[J]．东北电力大学学报，2017，37(3)：33-38．

XU Z Y，WANG X Y，XU D G，et al．Research on dynamic reactive power optimization based on improved PSO[J]．Journal of Northeast Electric Power University，2017，37(3)：33-38．

[10]黄俊辉，汪惟源，王海潜，等．基于模拟退火遗传算法的交直流系统无功优化与电压控制研究[J]．电力系统保护与控制，2016，44(10)：37-43．

HUANG J H，WANG W Y，WANG H Q，et al．Study of hybrid genetic algorithm and annealing algorithm on reactive power optimization and voltage control in AC/DC transmission system[J]．Power System Protection and Control，2016，44(10)：37-43．

[11]李军，周冬冬，张玉琼，等．基于AGSO-BAS混合算法的配电网分布式电源优化配置[J]．电力电容器与无功补偿，2019，40(6)：87-93．

LI J，ZHOU D D，ZHANG Y Q，et al．Distributed generation optimization configuration of distribution grid based on AGSO-BAS hybrid algorithm[J]．Power Capacitor & Reactive Power Compensation，2019，40(6)：87-93．

[12]郑能，胡瑞馨，丁晓群，等．考虑多种类型的分布式电源和网络重构的配电网无功优化[J]．智慧电力，2019，47(3)：90-96．

ZHENG N，HU R X，DING X Q，et al．Reactive power optimization of distribution network considering multiple types of distributed generations and network reconfiguration[J]．Smart Power，2019，47(3)：90-96．

[13]陈珩．电力系统稳态分析[M]．北京：中国电力出版社，2007：16-19．

CHEN Y．Steady state analysis of power system [M]．Beijing：China Electric Power Press，2007：16-19．

[14]赵勇，洪潮，黄河，等．发电机组的动态无功特性及影响因素[J]．南方电网技术，2015，9(2)：30-35．

ZHAO Y，HONG C，HUANG H，et al．Dynamic reactive power characteristics of generator units and influencing factors[J]．Southern Power System Technology，2015，9(2)：30-35．

[15]吕志鹏，盛万兴，钟庆昌，等．虚拟同步发电机及其在微电网中的应用[J]．中国电机工程学报，2014，34(16)：2592-2603．

LÜ Z P，SHENG W X，ZHONG Q C，et al．Virtual synchronous generator and its applications in micro-grid[J]．Proceedings of the CSEE，2014，34(16)：2592-2603．

[16]周挺，黄慧，刘林，等．基于调相机的直流近区电压无功协调优化方法[J]．智慧电力，2019，47(11)：54-59，66．

ZHOU T，HUANG H，LIU L，et al．Coordinative optimization method of reactive power in DC vicinity based on synchronous condenser．Smart Power，2019，47(11)：54-59，66．

[17]叶峰，丁玉珏，黄玉梅，等．基于模糊控制的电网动态无功控制技术研究[J] ．智慧电力，2019，47(9)：59-65．

YE F，DING Y J，HUANG Y M，et al．Dynamic reactive power control technology of power network based on fuzzy control．Smart Power，2019，47(9)：59-65．

[18]国家能源局．电力变压器用真空有载分接开关使用导则：DL/T 1538-2016[S]．北京：中国标准出版社，2016．

National Energy Administration．Application guide for vacuum on-load tap-changers for power transformers：DL/T 1538-2016[S]．Beijing，China：China Standard Press，2016．

Research on Day Ahead Dynamic Reactive Power Optimization Based on Generator Operation

LU Bin1, GAO Shan2*, LI Desheng1

(1. Wanbang Digital Energy Co., Ltd., Changzhou 213164, Jiangsu Province, China;2. School of Electrical Engineering, Southeast University, Nanjing 210096, Jiangsu Province, China)

In order to solve the practical problem of 24-hours dynamic reactive power optimization in power system dispatching, this paper divided generator’s operation into three regions in PQ mathematical model, according to the limit output range of generator’s operation. Moreover, the action times of discrete control equipment were taken as global inequality constraints, and a complete 24-hours non-linear mixed integer dynamic reactive power optimization mathematical model was established. The simulation results show that the mathematical model in this paper can adjust the output of generators according to the actual situation effectively when the generators are in phase-leading operation. In addition, increasing the number of control equipment’s action can reduce the loss of active power in the whole network, but at the same time, the frequent operation will greatly increase the probability of failure of equipment. It is necessary for us to find the appropriate constraints of the action number within the range of reliable acceptance of network losses, so as to save the comprehensive cost of the actual power grid operation.

dynamic reactive power optimization; generator safe operating limit; interior point method; power system dispatching

10.12096/j.2096-4528.pgt.20046

TM 74

2020-06-24。

(责任编辑 杨阳)