基于数据学习的新能源高渗透电网频率风险评估

温佳鑫，卜思齐*，陈麒宇，周博文

基于数据学习的新能源高渗透电网频率风险评估

温佳鑫1，卜思齐1*，陈麒宇2，周博文3

（1．香港理工大学电机工程学系，香港特别行政区 九龙区 999077；2．中国电力科学研究院有限公司，北京市 海淀区 100192；3．东北大学信息科学与工程学院，辽宁省 沈阳市 110819）

新能源正在逐步代替传统发电厂为用户提供电能，但同时也为电网的安全运行带来了潜在的风险。因此，在规划阶段需要全面地对最大频率偏差越线风险进行概率评估。基于蒙特卡罗仿真(Monte Carlo simulation，MCS)的规划方法效率很低，而人工神经网络(artificial neural network，ANN)可以通过对数据的学习做出快速有效的预测。为此，提出一种基于MCS-ANN的区域频率概率评估方法，以实现对区域最大频率偏差越线风险的快速评估。首先，产生大量的随机扰动，仅对小部分扰动进行仿真；然后将这部分数据送入ANN进行训练，并将剩余的大部分扰动送入训练好的ANN进行输出预测；重复以上训练和预测的过程，将多次预测结果的平均值作为最终的预测输出，得到各个风险区间的概率分布情况。最后，在IEEE 10机39节点的系统上验证了所提方法的有效性。

新能源；电网安全；频率风险评估；蒙特卡罗仿真(MCS)；神经网络(ANN)

0 引言

用新能源代替传统的发电厂来为用户提供优质电能是电力系统发展的趋势[1-8]。但是，新能源波动的随机性导致了不稳定的发电功率，从而增加了电网供电系统的不确定性，也为电网的安全运行带来了潜在的风险[9-11]。其中，电网供需不平衡最直接的表现就是频率的变化，当频率超过电网所规定的范围时，会有发电机退出运行或者引发低频减载来保证系统的安全运行[12]。因此，合理地评估新能源发电厂接入电网后的频率越线风险具有重要意义[13]。

在电力系统中，系统频率是一个虚拟的集成概念，用来表征系统的平均频率[14]。对于一个大型互联电网，系统局部频率的变化以及相应的越线风险无法被准确地评估，但针对每一台发电机都进行频率评估又不切实际，因此，评估一个区域的频率越线风险更具有现实意义。

为了减少新能源电厂给系统所带来的潜在风险，常规做法是提供充足的旋转备用，以保证系统在极端情况下也能稳定运行[15]。其中，极端情况指的是所有并网的新能源电厂都处在最大功率输出的情况，但这种情况在新能源渗透率高的电网中很少发生[16]。首先，不同类型的新能源具有不同的发电时段，如光伏电站白天发电，而风电场可以随时发电；其次，相隔较远的相同类型的新能源具有不同的时空分布，当2个风电场相距超过1200km时，其风速相关度为0[17]。这2点因素都表明极端情况出现的概率较低。所以，仅仅考虑频率的越线情况而忽视其出现的概率，则会增加系统的运行成本或是限制了新能源的大规模利用。因此，从严重性和出现概率2个角度综合评估区域频率的稳定情况更加合理。目前主要应用的方法为蒙特卡罗仿真(Monte Carlo simulation，MCS)，通过产生大量的随机扰动数据及其相应的仿真结果，统计得到所关心指标的概率分布[18-20]。在文献[18]中，先产生大量的随机场景，然后计算各个区域间最大传输能力的概率分布。在文献[19]中，MCS方法被用来评估配电网的可靠性。在文献[20]中，一种基于场景的MCS方法被用来计算频率稳定情况下的最大风能渗透率。虽然MCS方法能提供准确的评估结果，但是耗时较长。

近些年发展起来的人工神经网络(artificial neural network，ANN)具有自主学习能力，可以根据一些已有的数据进行学习和快速预测[21-24]。神经网络被广泛地应用于微网的不同等级控制中，以满足电能的质量、经济以及效率等方面的要求[21]。在文献[22]中，自适应神经网络被用来控制超导储能系统，以提供风机的暂态稳定性。文献[23]采用不同的神经网络模型来预测光照强度。神经网络可以通过学习、自主建模来对未知事件进行有效的预测与控制。

合理地结合ANN和MCS方法，可缩减系统风险评估所需要的时间。因此，本文提出一种基于MCS-ANN的区域频率风险概率评估方法，并在IEEE 10机39节点的系统上验证其有效性。

1 区域最大频率偏差概率评估

1.1 新能源的随机建模

相同或不同的新能源在不同时间尺度下具有不同的分布特性，因此，在不同时间尺度下的区域频率风险评估需要采用不同的随机模型[25]。本文以最常见的风速和光照时间的分布为例，用于不同规划目标下的风能光能随机模型如图1所示。在短期规划中，风速和光照时间分布均为Beta分布；而在中长期规划中，风速分布为Weibull分布，光照时间分布为正态分布。

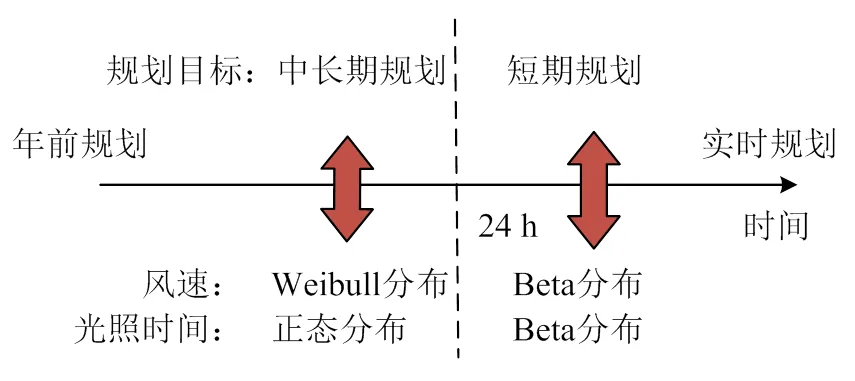
图1 用于不同规划目标下的风能光能随机模型

本文以风能的中长期规划为例进行研究，风速分布为Weibull分布。在大多数情况下，风功率w和风速的转换关系为线性的，具体关系如图2和式(1)[26]所示。

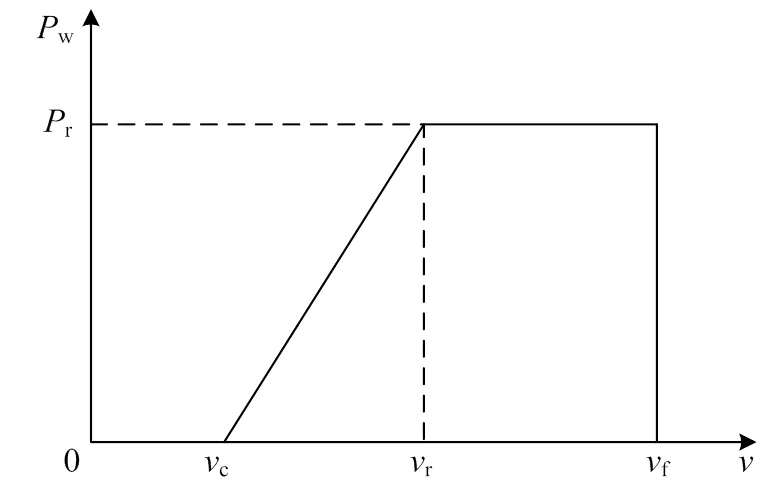
图2 风速与风功率的转换关系

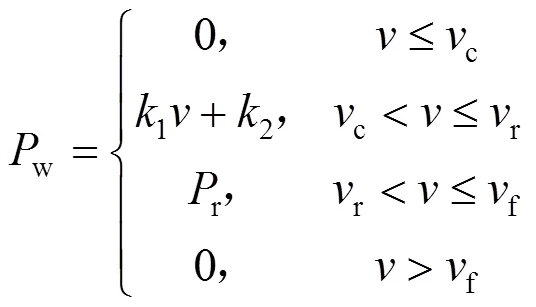
式中：c为切入风速；r为额定风速；f为切出风速；r为单台风机的额定功率；1和2为相应的计算系数，表达式分别为：

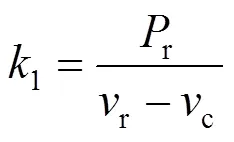
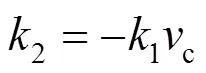
根据统计原理以及风速与风功率的转换关系，风功率的概率分布[25,27]表示如下：

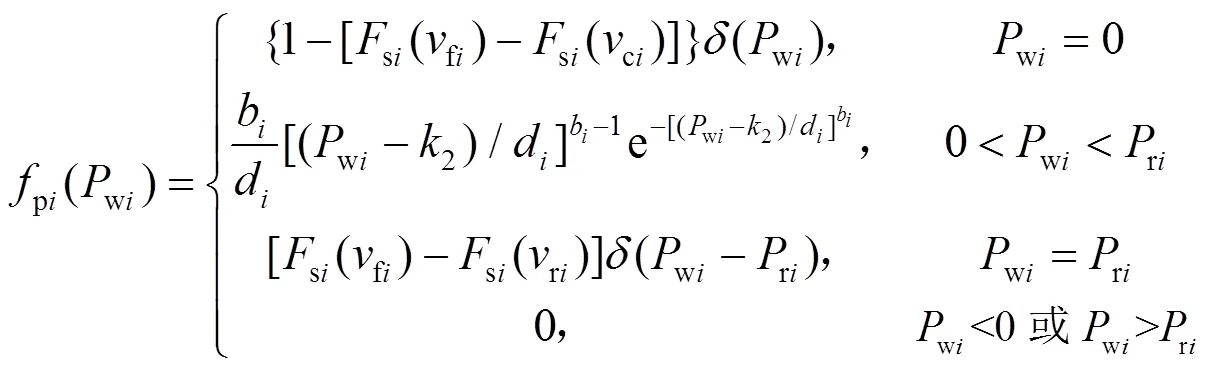
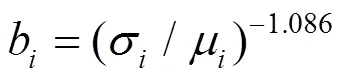
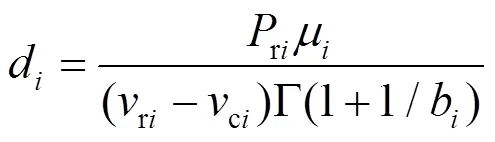
1.2 区域频率响应

在系统遭受到来自新能源的扰动后，各台发电机的频率会根据扰动的大小和位置，网络结构及自身调节参数的不同而有所差异。有些发电机的频率会呈上升趋势，而有些则会呈下降趋势，在调速器的作用下会达到一个稳态值，但这种波动的情况无法被系统平均频率所表征，扰动下的多机频率响应如图3所示。因此，观测一个大型电网的区域频率更有意义。

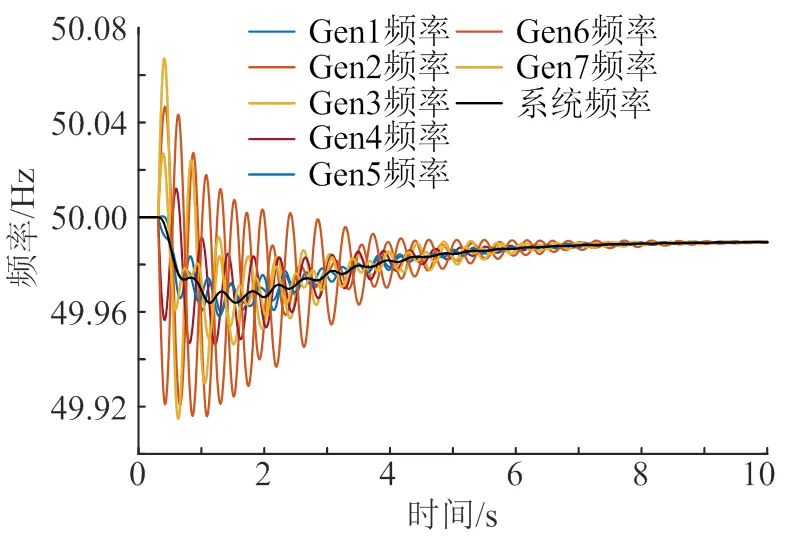
图3 扰动下的多机频率响应

系统频率根据转动惯量中心集成而得[28]，首先将各台发电机的转动惯量进行归一化：

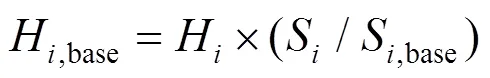
式中：Hbase为发电机在基准容量下的转动惯量；H为发电机在自身容量下的转动惯量；S为发电机的容量；Sbase为选取的基准容量。

转动惯量中心COI、系统频率system分别为：

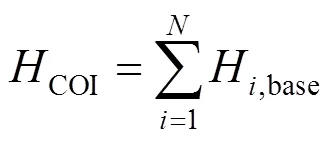
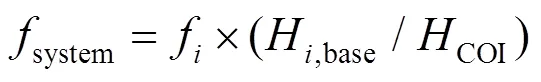
式中：f为发电机的频率响应；为系统所含有的发电机个数。

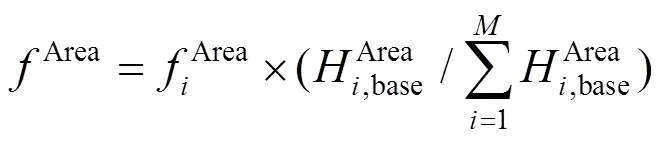
式中为该区域所包含的发电机的个数。

当频率波动到某些数值时，则会引起调度员的注意，并采取相应的动作以维持系统频率稳定，如增加或者减少某些发电机的出力。其中最重要的指标为频率运行上下限和规定上下限[29]。

因此，本文针对这些频率区间进行概率评估，其结果反映了新能源对电网频率影响的程度，进而为规划新能源并网及旋转备用容量提供参考。

2 基于MCS-ANN的区域频率概率评估

神经网络是由大量的简单神经元相互连接而成的自适应非线性动态系统，通过对已有样本的学习和训练来构建输入–输出的映射关系。一个训练好的神经网络可以快速有效地预测一个未知输入的结果，进而节省大量的时间。

每一个神经元的结构组成如图4所示，其中={1,2,…,x}为输入，={1,2,…,w}为连接权重，为神经元的输入个数，为偏置，计算结果被送入激活函数中，最终形成输出[30]。

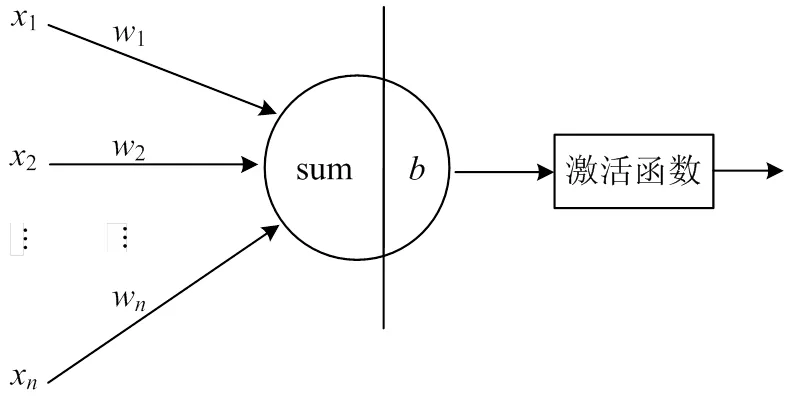
图4 神经元结构

神经网络由输入层、隐含层和输出层组成，其中隐含层可以是多层，如图5所示。

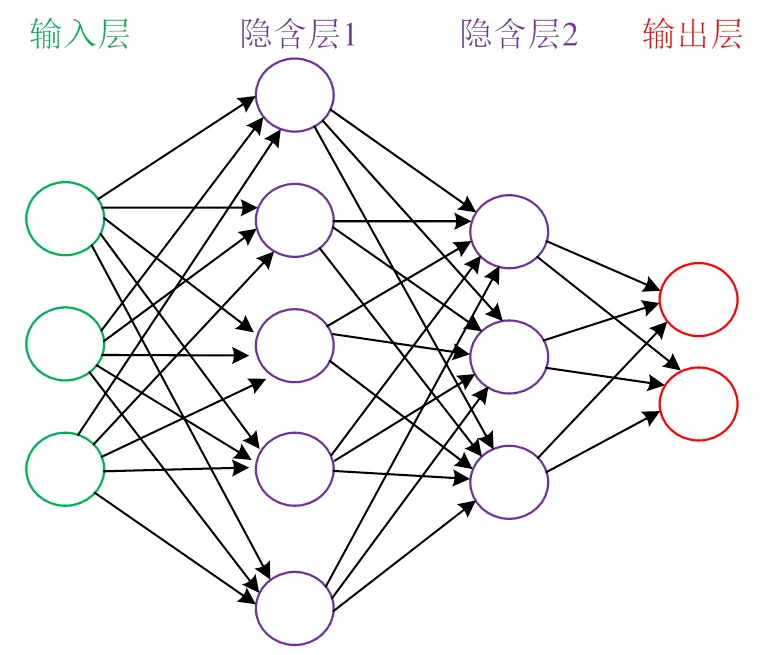
图5 神经网络结构图

首先对神经元参数和进行随机赋值，根据神经元的计算方式和网络连接计算得到输出，由这个输出与所给的真实样本结果的差值进行反向计算，更新和的数值，直到得到一个全局最小的偏差。

神经网络的初始值和一般是随机给定的，其结果一般具有不可重复性。为了保证该方法的有效性，将神经网络对某一组特定的样本进行次学习后所预测出来的不同结果进行平均化，将其作为该模型的预测结果。基于MCS-ANN的区域频率概率评估流程如图6所示，具体如下：

1）根据评估目标和新能源类型，选择合适的分布特性并产生大量的蒙特卡罗数；

2）根据新能源特性及其功率转换关系得到发电功率分布，将一小部分的扰动功率进行仿真，然后将该扰动功率及其对应的仿真结果送入神经网络中进行学习，并得到训练好的模型；

3）将之前没有用于仿真的扰动功率送入训练好的模型中，得到预测结果，之后重复以上学习、训练与预测的过程−1次，将这次预测结果取平均值，作为最终的输出结果，最后统计结果并得到各个区间的概率分布。

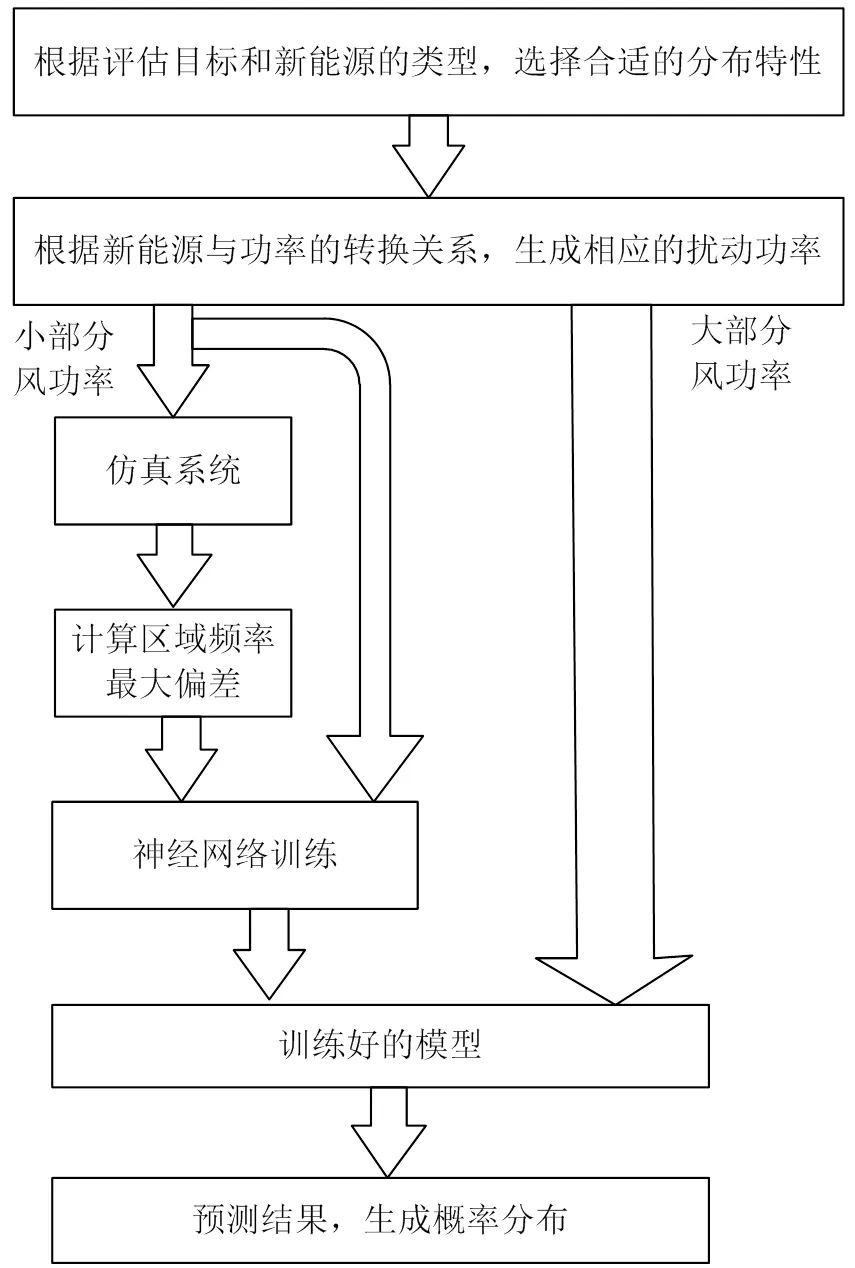
图6 基于MCS-ANN的区域频率概率评估流程

3 算例分析

为了验证基于MCS-ANN的区域频率概率评估方法的有效性，本文采用IEEE 10机39节点作为测试系统[31]。3个容量均为100MW风电场分别安装在节点10、23和29处，风电场的稳态输出为装机容量的2/3，这部分代替与之并联的发电机(G6, G7和G9)的稳态输出功率。其中，切入风速为4m/s，额定风速为10m/s，切出风速为22m/s，平均风速为8m/s，风速的方差为2.5，转动惯量为标准参数范围3~6s[12]。调速器的控制参数如下：调速器增益为0.05，高压涡轮系数H为0.4，再热时间常数R为10s。采用slow coherency identification[32]的方法将系统分为Area 1、Area 2、Area 3共3个区域，如图7所示。本文选用3个神经元作为输入层，为3台风机的随机扰动；2个隐含层依次为8个神经元和4个神经元；输出层有4个神经元，分别为系统和3个区域的最大频率偏差。数据中的70%用于训练，15%用于测试，15%用于验证。

根据英国国家电网的运行标准[29]，系统频率的运行上、下限分别为50.2Hz和49.8Hz，而规定的上、下限分别为50.5Hz和49.5Hz。因此，本文对这段几个频率区间进行概率评估。

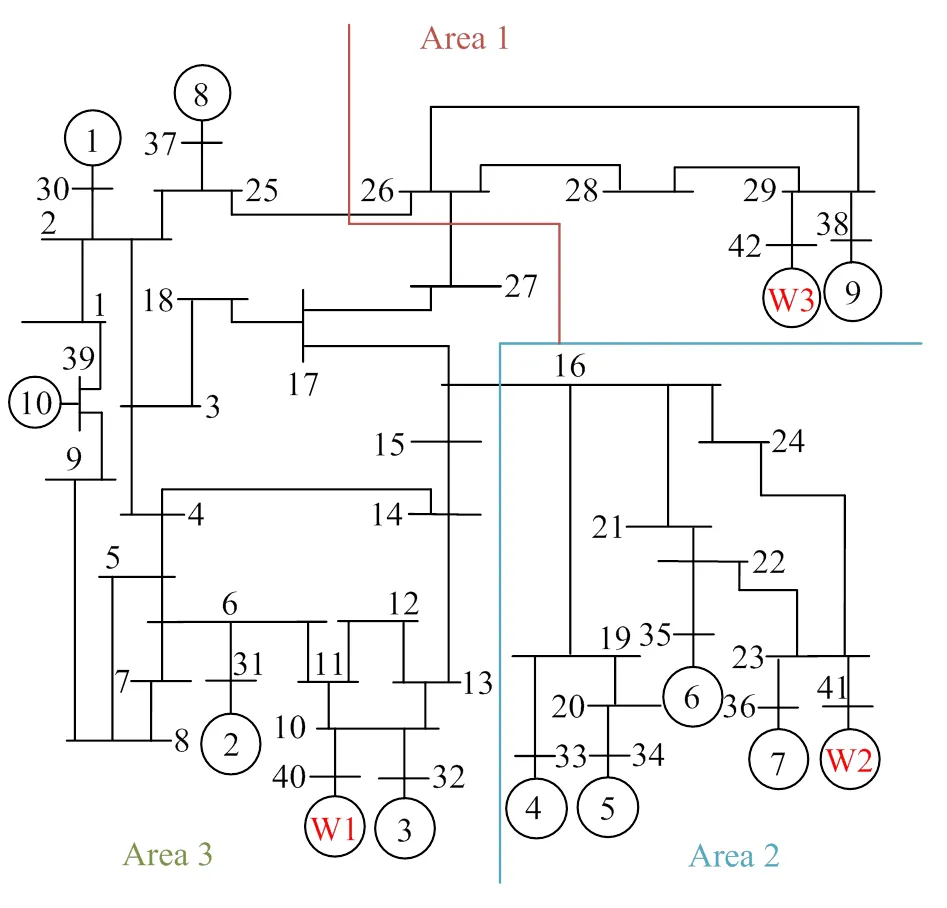
图7 含有3台风机的IEEE 10机39节点测试系统

根据Weibull分布产生5000组随机风速变量，其中随机选取100组数据进行仿真，分别获得系统和3个区域频率的最大偏差。将这组含有风机扰动和输出结果的数据送入神经网络进行学习。将余下的4900组风机波动功率送入刚刚训练好的神经网络中并得到预测结果。重复以上过程，最终得到系统和3个区域的最大频率偏差的平均预测结果。

将MCS-ANN方法的预测结果和MCS方法的标准结果进行对比，系统和3个区域的最大频率偏差误差分布分别如图8—11所示，可见大部分误差分布在−0.01~0.01Hz，证明MCS-ANN方法可较准确地预测系统和区域的最大频率偏差。

表1—4分别为系统和3个区域的最大频率偏差的概率分布。通过对比MCS-ANN和MCS方法的概率评估结果可以证明，MCS-ANN方法可以较准确地评估最大频率偏差的越线风险。由 表1可以看出，在某些情况下系统的频率会低于49.5Hz。在基于最极端情况下的传统分析中，该容量大小的风电并网会使系统不稳定，需要一些额外的措施来降低风险，如增加旋转备用，这极大地限制了风能的接入。概率评估可以为调度员提供一个量化的结果，如频率低于49.5Hz的概率为1.8%，再结合电网要求及调度员经验进行最终的判断。如果电网可以接受2%的频率(49.5Hz)越线风险，则该容量大小的风电可以并网，否则需要进一步的规划。该二维概率评估方法可以加大电网对新能源的利用。

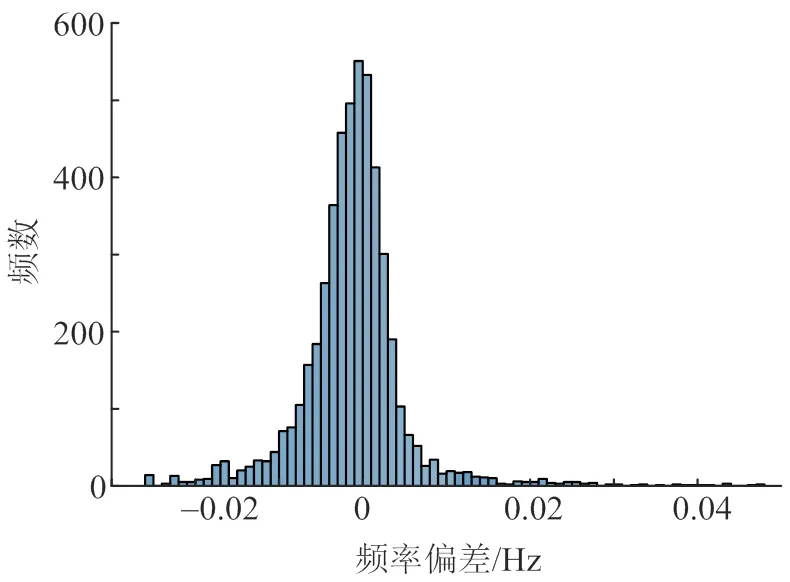
图8 系统最大频率偏差误差分布直方图

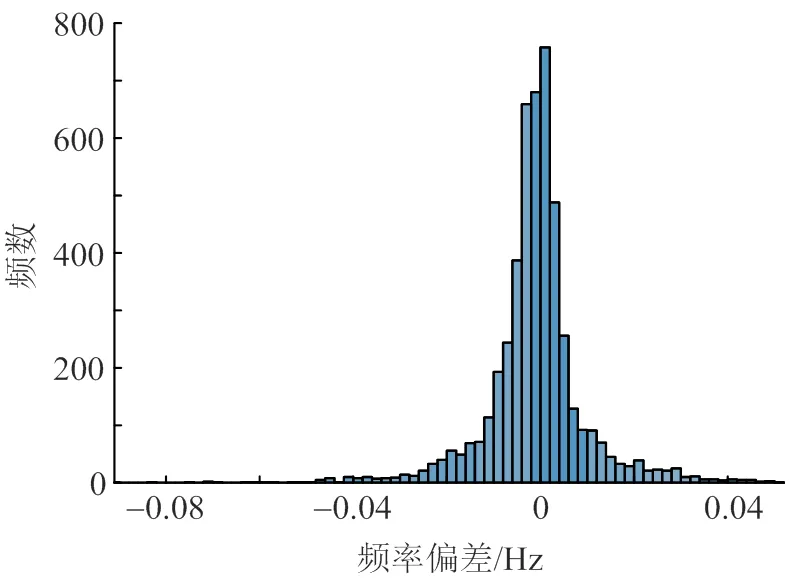
图9 Area 1最大频率偏差误差分布直方图

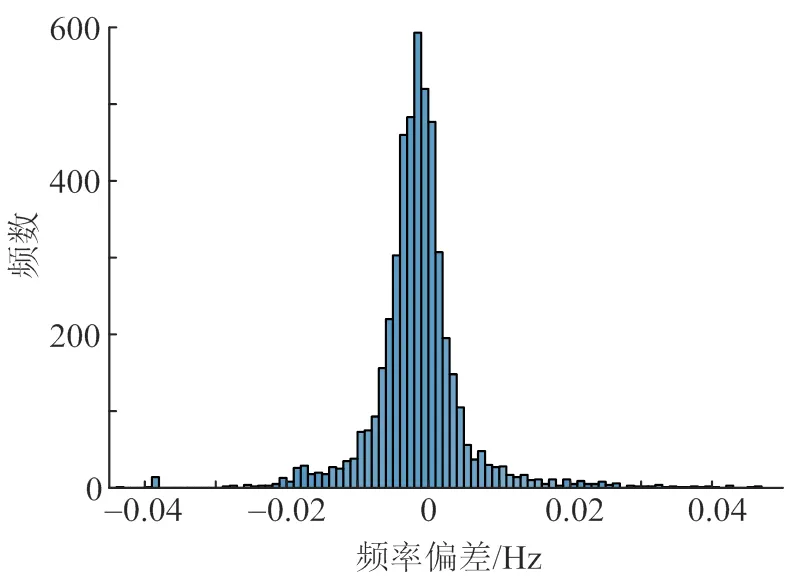
图10 Area 2最大频率偏差误差分布直方图

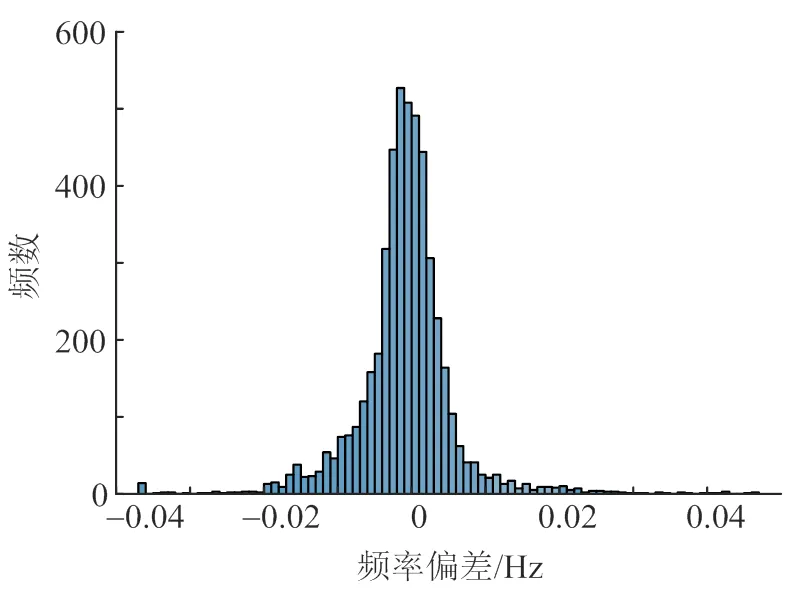
图11 Area 3最大频率偏差误差分布直方图

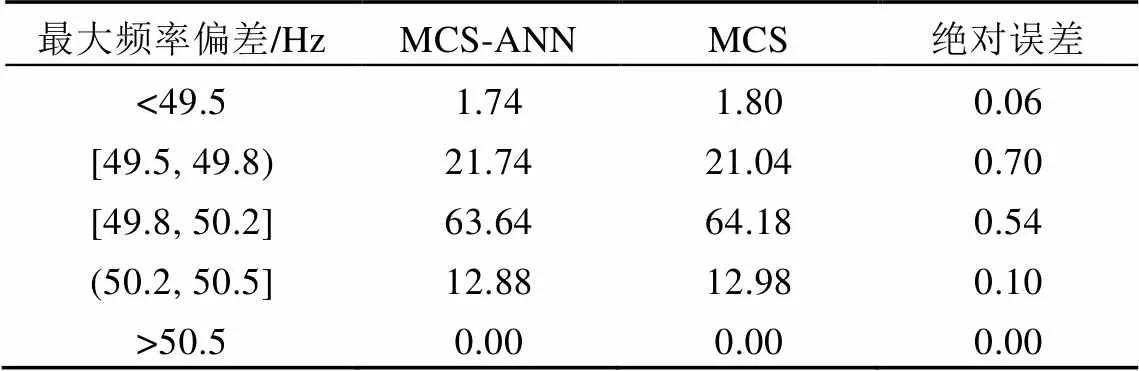
表1 系统最大频率偏差的概率分布

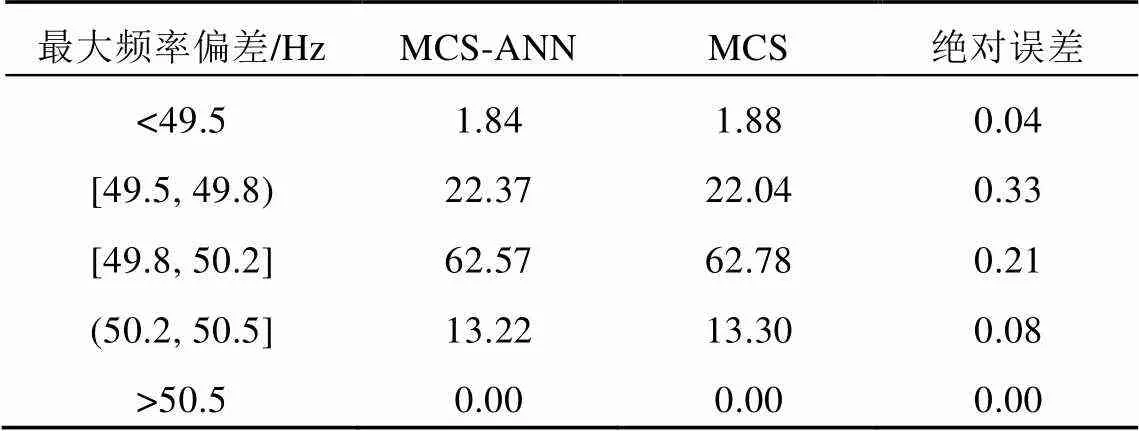
表2 Area 1最大频率偏差的概率分布

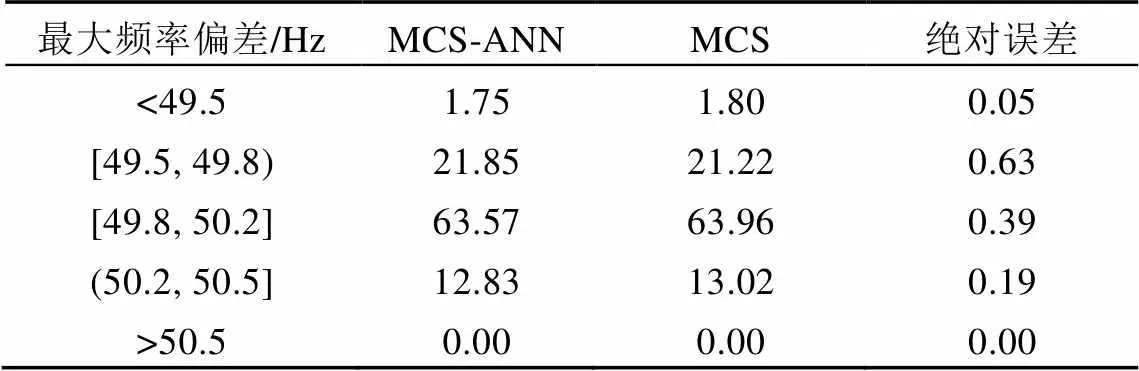
表3 Area 2最大频率偏差的概率分布

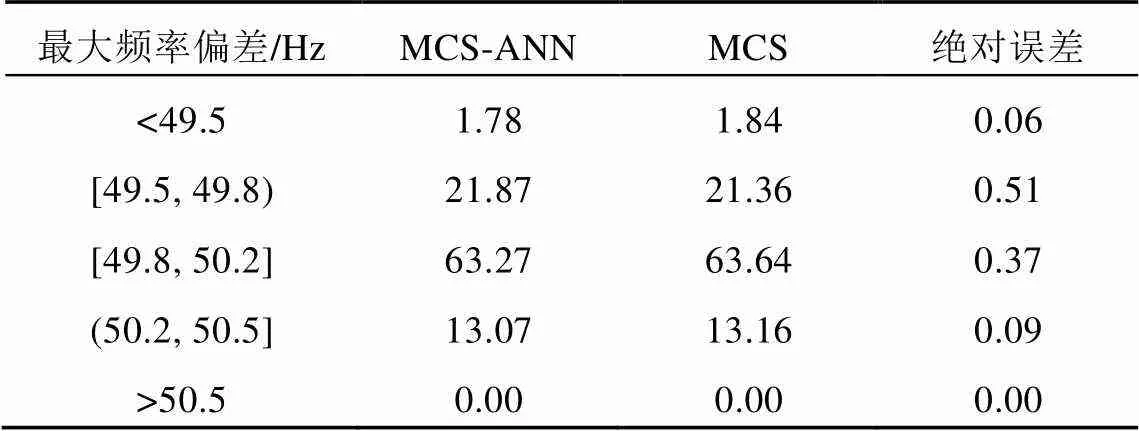
表4 Area 3最大频率偏差的概率分布

表5对比了MCS-ANN与MCS方法的计算时间，可见，MCS-ANN方法仅仅需要714.4s，是MCS方法所需计算时间的2%，证明了MCS-ANN方法的高效性。

表5 MCS-ANN与MCS方法的计算时间对比

4 结论

相对于传统的基于极端情况的评估，从概率角度评估新能源并网所导致的各个区域频率越线情况，以百分比形式量化了频率越线程度，可以更加全面地对频率越线风险进行评估，进而增加了大规模新能源并网的可能性。

提出一种基于MCS-ANN的区域频率概率评估方法，相比于单纯的MCS方法，该方法应用ANN的快速学习、训练与预测的特性来加速概率评估过程，将评估时间缩短为原来的2%。为了保证该方法的有效性与稳定性，取相同数据的10次学习以及相应预测结果的平均值作为最终预测输出，通过将其与MCS方法的标准结果进行对比可知，该方法的预测误差较小，可以较准确地预测系统和区域的最大频率偏差。

[1]LI T，LI A，GUO X P．The sustainable development-oriented development and utilization of renewable energy industry：a comprehensive analysis of MCDM methods[J]．Energy，2020，212：118694．

[2]潘旭东，黄豫，唐金锐，等．新能源发电发展的影响因素分析及前景展望[J]．智慧电力，2019，47(11)：41-47．

PAN X D，HUANG Y，TANG J R，et al．Influencing factors and prospects for development of renewable energy power generation[J]．Smart Power，2019，47(11)：41-47．

[3]LU C，FENG Y W，FEI C W，et al．Improved decomposed-coordinated kriging modeling strategy for dynamic probabilistic analysis of multicomponent structures[J]．IEEE Transactions on Reliability，2020，69(2)：440-457．

[4]武志军．综合能源服务下新能源集约化管控评价方法[J]．华电技术，2019，41(12)：68-71．

WU Z J．Evaluation method on new energy intensive management for integrated energy services[J]．Huadian Technology，2019，41(12)：68-71．

[5]杜文娟，卜思齐，王海风．考虑并网风电随机波动的电力系统小干扰概率稳定性分析[J]．中国电机工程学报，2011，31(S1)：7-11．

DU W J，BU S Q，WANG H F．Effect of stochastic variation of grid-connected wind generation on power system small-signal probabilistic stability[J]．The Proceedings of the CSEE，2011，31(S1)：7-11．

[6]KROPOSKI B．Integrating high levels of variable renewable energy into electric power systems[J]．Journal of Modern Power Systems and Clean Energy，2017(5)：831-837．

[7]李克勋，宗明珠，魏高升．地热能及与其他新能源联合发电综述[J]．发电技术，2020，41(1)：79-87．

LI K X，ZONG M Z，WEI G S．Overview of geothermal power generation and joint power generation with other new energy sources[J]．Power Generation Technology，2020，41(1)：79-87．

[8]朱罡，王茂春．含新能源发电的电力系统状态估计研究[J]．电网与清洁能源，2020，36(4)：32-40．

ZHU G，WANG M C．Review on state estimation for power system containing renewable energy generation[J]．Power System and Clean Energy，2020，36(4)：32-40．

[9]LI R，GENG H，YANG G．Fault ride-through of renewable energy conversion systems during voltage recovery[J]．Journal of Modern Power Systems and Clean Energy，2016(4)：28-39．

[10]段建民，王志新，王承民．基于电网聚合模型的新能源接纳能力评价与分析[J]．分布式能源，2019，4(5)：42-49．

DUAN J M，WANG Z X，WANG C M．Evaluation and analysis of the capability of new energy integration based on grid aggregation mode[J]．Distributed Energy，2019，4(5)：42-49．

[11]李更丰，邱爱慈，黄格超，等．电力系统应对极端事件的新挑战与未来研究展望[J]．智慧电力，2019，47(8)：1-11．

LI G F，QIU A C，HUANG G C，et al．New challenges and future research prospects in power system against to extreme events[J]．Smart Power，2019，47(8)：1-11．

[12]KUNDUR P．Power system stability and control[M]．McGraw-Hill New York：Spring，2013．

[13]马世英，王青．大规模新能源集中外送系统源网协调风险及仿真评估[J]．发电技术，2018，39(2)：112-117．

MA S Y，WANG Q．Risk and simulation evaluation of large-scale centralized new energy sending system [J]．Power Generation Technology，2018，39(2)：112-117．

[14]SHI Q，LI F，CUI H．Analytical method to aggregate multi-machine SFR model with applications in power system dynamic studies[J]．IEEE Transactions on Power Systems，2018，33(6)：6355-6367．

[15]BU S，WEN J，LI F．A generic framework for analytical probabilistic assessment of frequency stability in modern power system operational planning[J]．IEEE Transactions on Power Systems，2019，34(5)：3973-3976．

[16]WEN J，BU S，ZHOU B，et al．A fast-algorithmic probabilistic evaluation on regional rate of change of frequency (RoCoF) for operational planning of high renewable penetrated power systems[J]．Energies，2020，13：2780．

[17]FRERIS L，LNFIELD D．Renewable energy in power system[M]．New York：Wiley，2008．

[18]BERIZZI A，BOVO C，DELFANTI M，et al．A Monte Carlo approach for TTC evaluation[J]．IEEE Transactions on Power Systems，2007，22(2)：735-743．

[19]HEYDT G T，GRAF T J．Distribution system reliability evaluation using enhanced samples in a Monte Carlo approach[J]．IEEE Transactions on Power Systems，2010，25(4)：2006-2008．

[20]AHMADYAR A，RIAZ A，VERBIC G，et al．A framework for assessing renewable integration limits with respect to frequency performance[J]．IEEE Transactions on Power Systems，2018，33(4)：4444-4453．

[21]LOPEZ-GARCIA T B，CORONADO-MENDOZA A，DOMÍNGUEZ-NAVARRO J A．Artificial neural networks in microgrids：a review[J]．Engineering Applications of Artificial Intelligence，2020，95：103894．

[22]MUYEEN S M，HASANIEN H M，AL-DURRA A．Transient stability enhancement of wind farms connected to a multi-machine power system by using an adaptive ANN-controlled SMES[J]．Energy Conversion and Management，2014，78：412-420．

[23]GUIJO-RUBIO D，DURÁN-ROSAL A M，GUTIÉRREZ P A，et al．Evolutionary artificial neural networks for accurate solar radiation prediction[J]．Energy，2020，210：118374．

[24]ZHANG X S，YANG B，YU T，et al．Dynamic surrogate model based optimization for MPPT of centralized thermoelectric generation system under heterogeneous temperature differences[J]．IEEE Transactions on Energy Conversion，2020，35(2)：966-976．

[25]BU S Q，DU W，WANG H F，et al．Probabilistic analysis of small-signal stability of large-scale power systems as affected by penetration of wind generation [J]．IEEE Transactions on Power Systems，2012，27(2)：762-770．

[26]王成山，郑海峰，谢莹华，等．计及分布式发电的配电系统随机潮流计算[J]．电力系统自动化，2005，24：39-44．

WANG C S，ZHENG H F，XIE Y H，et al．Probabilistic power flow containing distributed generation in distribution system[J]．Automation of Electric Power Systems，2005，24：39-44．

[27]KENDALL M．Kendall’s advanced theory statistics[M]．New York：Oxford University Press，1987．

[28]ANDERSON P M，FOUAD A A．Power system control and stability[M]．Ames，IA：Iowa State University Press，1977．

[29]National Electricity Transmission System Security and Quality of Supply Standards[S]．UK：National Grid ESO，2014．

[30]AGATONOVIC-KUSTRIN S，BERESFORD R．Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research[J]．Journal of Pharmaceutical and Biomedical Analysis，2000，22(5)：717-727．

[31]ROGERS G．Power system oscillations[M]．Norwell，MA：Kluwer，2000．

[32]CHOW J H，CULLUM J，WILLOUGHBY R A．A sparsity-based technique for identifying slow-coherent areas in large power systems[J]．IEEE Transactions on Power Apparatus and Systems，1984，103(3)：463-473．

Data Learning-based Frequency Risk Assessment in a High-penetrated Renewable Power System

WEN Jiaxin1, BU Siqi1*, CHEN Qiyu2, ZHOU Bowen3

(1. Department of Electrical Engineering, The Hong Kong Polytechnic University,Kowloon District, Hong Kong S.A.R. 999077, China; 2. China Electric Power Research Institute,Haidian District, Beijing 100192, China; 3. College of Information Science and Engineering, Northeastern University, Shenyang 110819, Liaoning Province, China)

Renewable energy is gradually replacing traditional power plants to provide electricity for users, but it also brings potential risks to the safe operation of the power grid. Thus, in the planning stage, it is necessary to comprehensively evaluate the probability of violation risk of maximum frequency deviation. Planning method based on Monte Carlo simulation (MCS) is inefficient, while artificial neural network (ANN) can make fast and effective prediction by learning data. Therefore, this paper proposed an MCS-ANN algorithm to realize the rapid assessment of violation risk of regional maximum frequency deviation. Firstly, a large number of stochastic disturbances were generated, and only a small part of disturbances were used for MCS. Then, these data were sent to the neural network for training, and most of the remaining disturbances were sent to the trained neural network for output prediction. The above training and prediction processes were repeated. The average of multiple prediction results was used as the final prediction output, and the probability distribution of each risk interval was obtained. Finally, the effectiveness of the proposed MCS-ANN algorithm was verified on IEEE 10-machine 39-node system.

renewable energy; power grid security; frequency risk assessment; Monte Carlo simulation (MCS); artificial neural network (ANN)

10.12096/j.2096-4528.pgt.20105

TK 81

国家自然科学基金(51807171)；香港研究资助局基金(15200418, 15219619)；广东省自然科学基金(2019A1515011226)。

Project supported by National Natural Science Foundation of China (51807171); Hong Kong Research Grants Council (15200418, 15219619); Natural Science Foundation of Guangdong Province (2019A1515011226).

2020-09-30。

(责任编辑 尚彩娟)