主动声纳接收信号建模研究*

2021-03-16

舰船电子工程 2021年2期

（上海船舶电子设备研究所上海 201108）

1 引言

主动声纳是探潜反潜的主要装备［1］，可以对安静型潜艇进行探测。目标回波信号作为主动声纳信号处理的基础，而根据试验所得到的接收信号中含有混响和环境噪声，目标回波信噪比低，无法提取目标回波信号。因此，在需要对主动声纳进行技术论证或对仿真系统进行性能评估时，声纳接收信号仿真模型的构建显得更为重要。

主动声纳接收信号可看作海洋混响、海洋环境噪声和目标回波信号的叠加。通过分析海洋混响的统计模型、目标回波模型、以及海洋环境噪声的模拟，可以实现主动声纳接收信号的建模及仿真。现有的主动声纳信号建模方法多数也是基于此实现的［2～4］。目标回波模型的构建是主动声纳接收信号建模的关键，本文在亮点回波模型及其相关理论的基础上［5～6］，考虑亮点之间的几何遮挡问题，提出一种更为细化的亮点遮挡面积计算方法，以精确模拟在不同态势下亮点回波的时延变化和强度起伏为目标，建立相应的目标亮点回波模型，并通过仿真分析进行验证。

2 主动声纳接收信号建模

2.1 海洋混响模拟

混响是主动声纳工作时特有的一种背景噪声，它是主动声纳发射的脉冲信号在照射到海洋中随机分布的散射体以及起伏的界面后产生的随机信号。混响生成流程图如图1所示。

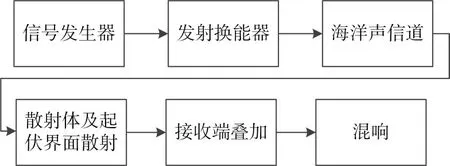
图1 混响生成流程图

混响虽然也是一种非线性非平稳的随机信号，不过其性质和海洋噪声却完全不同。混响最能区别于噪声海洋环境的特征就是混响与发射信号波形有一定的相关性，且混响强度和发射信号的能量呈正相关的关系。

远距离探测声纳一般发射长脉冲信号，在发射脉宽增大时，可以将发射信号的混响看作多个连续发射的短脉冲所产生的混响迁都的累加。混响强度可以表示为

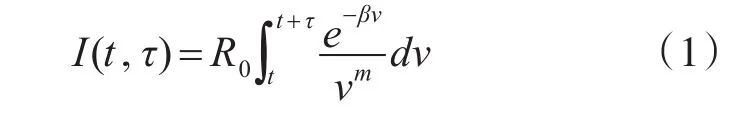
其中R0是和t，τ无关的系数；β是指数衰减系数，一般是由于海水吸收和边界损失有关。m的大小与混响的机理、传播条件等因素有关［7］。

本文旨在建立能够反映混响规律及特征的混响模型，根据混响的统计模型与混响强度公式可以得到模拟混响。假设发射信号是中心频率为2000Hz，带宽为30Hz的LFM信号，脉冲宽度为1s，仿真得到的混响波形图及时频分析如图2和图3

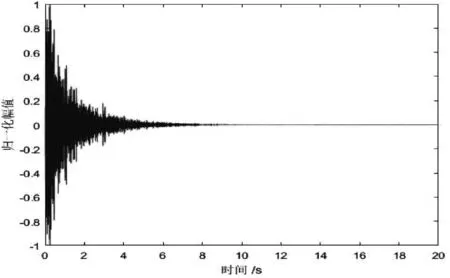
图2 窄带LFM混响波形

图3 混响时间-频率历程图

2.2 海洋环境噪声

构成海洋环境噪声的主要噪声源有潮汐、海底湍流、地震扰动、航船噪声及风成噪声等，多种噪声源合成的环境噪声存在于海洋中的任意时刻和所有地点。实际的海洋噪声具有时变性和无期望性，因而不可能用一个确定的数学模型来描述。在实际仿真中，根据海洋环境噪声谱级与高斯白噪声的频域信息，即可模拟所需要的环境噪声。海洋环境噪声谱级参照浅海噪声谱级经验公式进行计算［8］。海洋环境噪声的仿真结构如图4所示。

图4 环境噪声序列仿真结构

仿真环境噪声频段设为0～30KHz，海况为三级，得到输出的仿真噪声序列如图5所示。

图5 海洋环境噪声波形

2.3 水下目标回波

亮点回波模型把水下目标看作一个响应系统，回波信号就是系统在照射信号激励下的响应。目标等效为多个亮点，目标回波则可看作多个亮点回波的总和。根据亮点模型理论，单个亮点传输函数是：

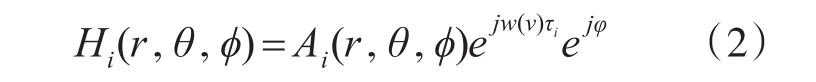
r是声纳到目标的距离，θ、φ分别是信号的水平入射角和垂直俯仰角，本文中假设声纳与目标同一深度，即取垂直俯仰角为0。Ai是亮点回波的幅度，w(v)是目标运动产生的多普勒频移，τi是亮点间由声程差引起的相对时延，φ则是回波信号的相位改变。因此对应多个亮点，其传输函数为

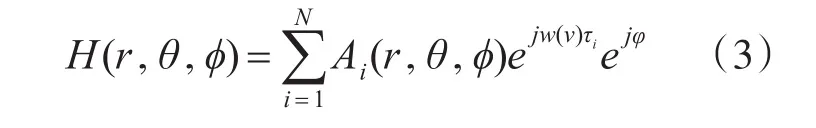
根据亮点回波模型和理论，选取简单潜艇模型作为目标，将图6所示水下目标的艇首、前艇体、舰桥、后艇体和艇艉等效为在同一条轴心线上的5个刚性球体来模拟目标亮点。

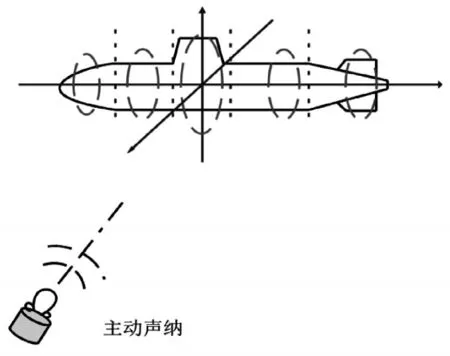
图6 水下目标的亮点模型

由于目标不同位置处的目标强度明显不同，为更好地模拟目标强度的差异性，可以将目标亮点细化为不同半径的刚性球体。根据文献［10］中给出的球体目标强度公式：

式中a为球体半径。同时又因为目标的结构复杂，不同亮点处的反射能力也不同，暂时不考虑声波在水中传播时的损失，定义反射系数ci为反射声强比上入射声强。以舰桥中心为参考点，参照文献［6，9］中建立的亮点模型，设置各亮点的相对位置、球体半径和反射系数如表1。

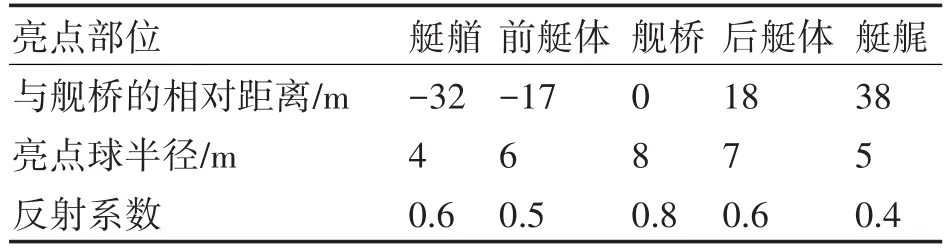
表1 各亮点参数

当入射声波以不同角度照射目标时，得到的有效散射面积也不同，映射到已建立的亮点模型，可以通过不同入射角度下刚性球体之间被遮挡的投影面积的变化来近似模拟各个亮点目标强度的改变。在仿真中，按照入射声波到达的时间先后对所有亮点进行排序，定义相应的遮挡系数Hij(θ)来表征前一个目标亮点刚性球体j对后一个目标亮点i的遮挡效果。亮点球体的目标强度与有效投影面积成正相关，遮挡系数的大小定义为刚性球体被遮挡的投影面积占该刚性球体全部投影面积的比值。

定义Sij为在入射方向上前一个亮点j在后一个亮点i上的投影面积，其具体计算表达式可归纳如下。

当刚性球体i半径大于刚性球体j时，遮挡面积Sij为

声纳与目标之间的相对运动将会产生多普勒频移。假设声纳固定不动，考虑目标在径向运动速度为v的情况下，其多普勒频移为

θ是声波入射角度，c为水下声速。

综合上述分析，得到目标的时域表达式为

其中φi是各亮点发生反射时产生的随机相位。τi是各亮点的传播时延：

r是声纳与水下目标之间的距离，Li是各亮点与参考点之间的相对距离。

基于本文建立的回波亮点模型，以高频信号对目标模型的所有舷角进行照射，并对接收到的回波信号进行匹配相关处理，得到如图7所示的目标模型二维散射图。从图中可以看出目标模型的二维散射图有以下特点：

图7 目标模型二维散射函数图

1）从艇艏和艇艉方向入射时，亮点之间彼此离散且跨越尺度大，亮点之间最大间隔与目标尺度相当；

2）入射方向趋向正横方向时，亮点间隔逐渐减小，个数在正横方向最少，且亮点背景弱；

3）不同的照射角度，各个亮点的显示强度有明显差异。

本文在对目标回波信号建模时忽略了声波在亮点之间的二次反射、绕射和再辐射等复杂过程，使仿真得到简化。根据实际测量和理论上的潜艇模型的二维声散射图都是典型的蝴蝶图［11～12］，其显著特征是各亮点的显示强度随着方位变化而变化，亮点之间尺度间隔最大在艇艏和艇艉入射方向，最小在正横方向。显然，这些特性与本文建立的亮点模型保持一致，也说明该建模方法可以模拟随水下目标态势变化的目标回波的时延变化和强度起伏。