分数阶时滞忆阻混沌电路的动力学分析及电路仿真*
2021-03-16翁业翠丁大为
王 匀 钱 鑫 翁业翠 丁大为
(1.中国电子科技集团公司第三十八研究所 合肥 230088)(2.安徽大学电子与信息工程学院 合肥 230601)
1 引言
在1971年之前,人们普遍认为基本电路元件是电阻、电感和电容。然而在蔡少棠教授[1]提出忆阻的概念之后,忆阻器的出现打破了人们对传统电子器件的认知。2008年,惠普实验室[2]首次实现了忆阻器的物理器件模型。目前大量文章[3~5]集中在整数阶的忆阻混沌系统的研究,但关于分数阶忆阻混沌系统的研究成果很少。1974年,Oldham和Spanier[6]给出了分数阶完整的数学表达。分数阶理论提供了更好的描述记忆和遗传特性的工具,利用分数阶算子更能客观地反映混沌系统动态电路的动力学现象和实际特性,因此许多研究成果[7~8]都集中在分数阶忆阻器模型和忆阻系统上。
目前已有相关文献研究了分数阶时滞忆阻系统的动力学行为。例如文献[9]研究一种分数阶忆阻器模型的本质特性和串并联电路的特性。文献[10]研究了最简分数阶时滞忆阻混沌系统的稳定性及其分岔行为等动力学行为。然而大多数研究仅限于数学模型的分析与仿真,没有实际具体电路仿真来验证。因此本文提出了一个基于分数阶的非线性时滞混沌电路,介绍了该系统的数学模型,以及对其进行了平衡点和稳定性分析,最后,通过Multisim软件给出了电路仿真,验证了理论分析和数值仿真的正确性。
2 分数阶时滞忆阻混沌电路建模与分析
Muthuswamy等实现了磁控忆阻器等效模型[11],如图1所示。有关求解分数阶微积分的方法很多[12~13]。本文中应用 Oustaloup[14]提出的近似技术来得到分数阶积分算子的近似传递函数来实现分数阶忆阻器,将其替换图1中的电容得到分数阶磁控忆阻器,数学表达式为

图1 磁控忆阻器示意图
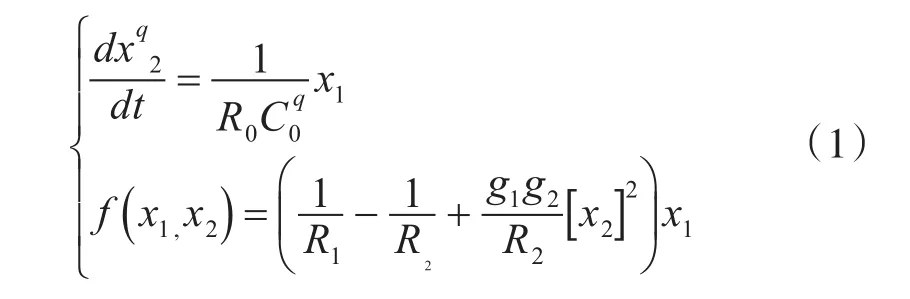
其中x1、x2和f(x1,x2)分别是忆阻器的输入、内部状态变量和输出。g1和g2是分别是乘法器M1和M2的放大倍数。令R0=8.2kΩ,R1=750Ω,R2=1.5kΩ,R3=R4=750Ω,g1=0.1,g2=1.3。分数阶磁控忆阻器的等效参数为α=0.6667ms和β=0.0087S/Wb,其中。 当 驱 动 信 号,其中X1=4V,分数阶忆阻器电流-电压曲线如图2所示。从图2(a)中可以看出,随着分数阶阶数的增加,磁滞回线的面积变大。图2(b)表示随着频率的增加,磁滞回线的面积减少。
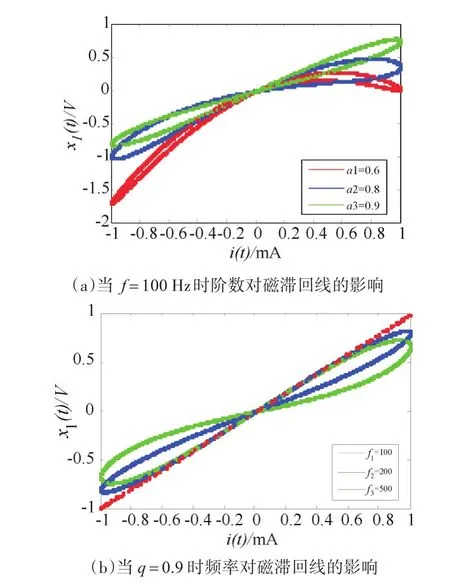
图2 磁控忆阻器磁滞回线图
将上述分数阶忆阻器模型应用到混沌电路中,电路结构如图3所示[15]。τ是时滞参数,电路的数学表达式见式(2),其中
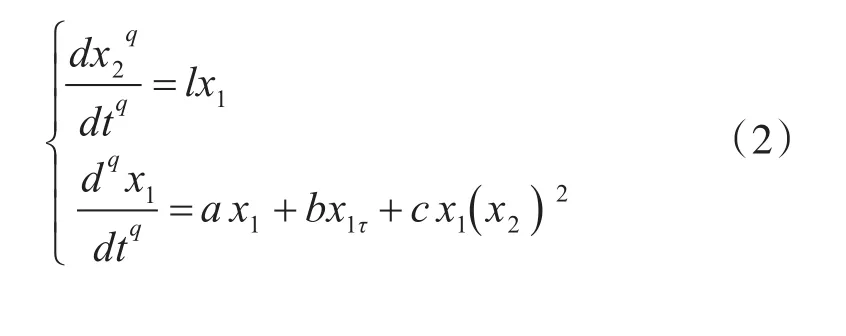
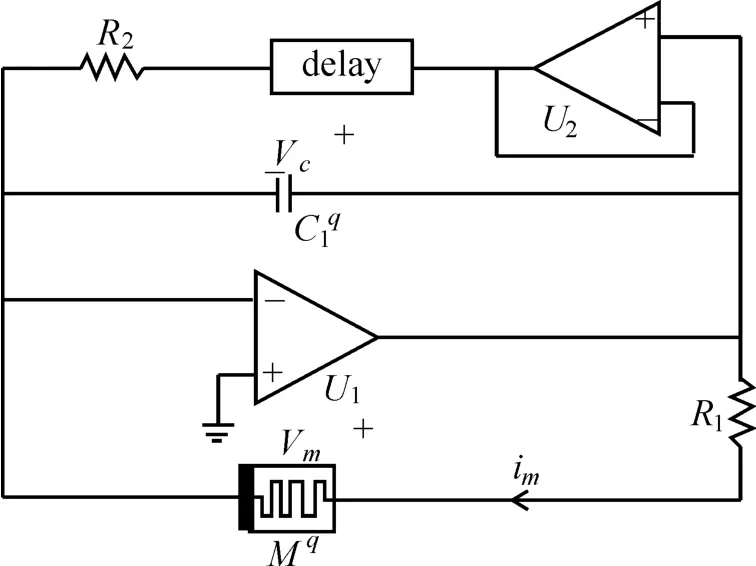
图3 分数阶时滞忆阻混沌电路
3 稳定性分析


4 仿真实验
数值仿真使用了改进的Adams-Bashforth-Moulton预估校正算法[16]来求解分数阶时滞微分方程。仿真软件为Matlab。设定系统参数q=0.9,l=2.5,b=-2,τ=1,使得参数a在[1.35,2]区间变化,见图4。从分岔图可以很明显地看出系统(2)的轨道从周期状态开始,然后当经过阈值时,出现Hopf分叉,最后随着a的增加变为混沌状态。各状态的相位图和时域图如图3所示。当a=1.62时,相位图与时域图如图5(a)和(d)所示,系统表现出一个稳定的极限环。当a=1.68时,系统进入混沌状态,如图5(b)和(e)所示。当a=1.73时,系统展现出双涡旋的混沌吸引子,如图5(c)和(f)所示。

图4 分岔图
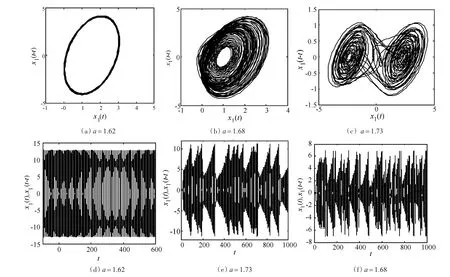
图5 相位图与时域图
为了验证理论分析和数值仿真的正确性,Multisim进行电路仿真。其中时滞电路采用APF(全通滤 波 器)[17~19]来 设计见图 6(b)。 分数阶阶数q=0.9,图6(a)中分数阶电容的电阻和电容数值分别 为R1=62.84MΩ,R2=0.25MΩ,R3=0.0025MΩ和C1=1.232μF,C2=1.835μF,C3=1.10μF 。运 算放大器和乘法器采用AD711KN和AD633JN,提供±15的电压和R=11.24kΩ,整体电路图如图6(c)所示。
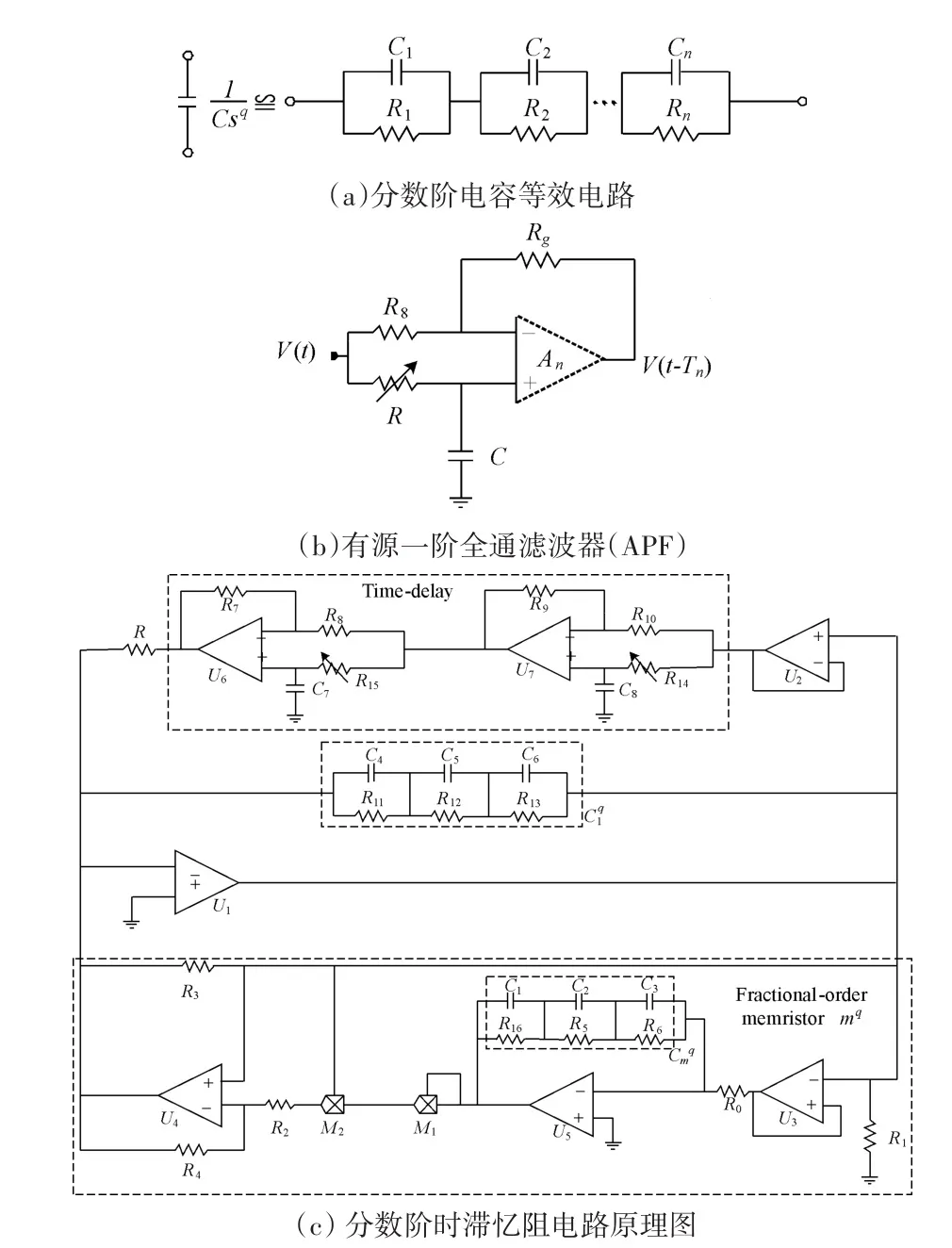
图6 电路结构图
电路仿真结果图如图7所示。仿真结果与图5吻合,验证了理论分析和数值仿真的正确性。
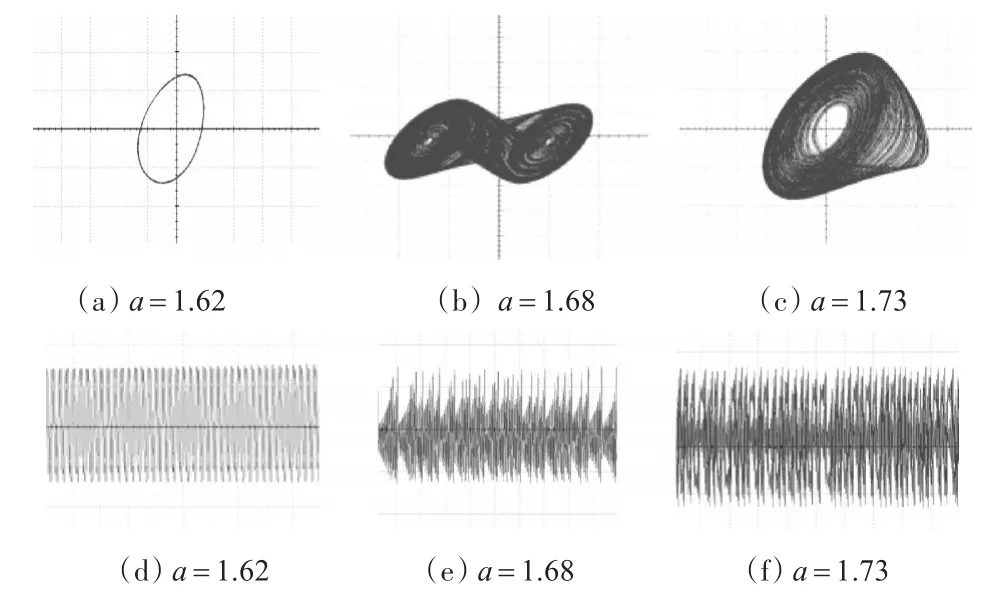
图7 Multisim电路仿真结果图
5 结语
在本文中,我们提出了一个分数阶忆阻器和基于此忆阻器的分数阶时滞忆阻混沌电路。通过理论分析和Matlab数值仿真,详细研究了此混沌电路的稳定性和一些动力学性质,包括平衡点、稳定性、分岔、相位图等。电路的动力学行为表现出极限环、单涡旋混沌吸引子和双涡旋混沌吸引子。此外,我们使用Multisim搭建了电路仿真,电路仿真与数值仿真结果完全一致。
