Spark平台上利用网络加权Voronoi图的分散迭代社区聚类并行化研究

颜 烨 张学文 王立婧

1(重庆大学城市科技学院电气信息学院 重庆 402167)

2(北华大学机械工程学院 吉林 吉林 132021)

0 引 言

近年来，通过观察在这一交互作用下的网络来分析真实世界的交互作用已经变得很普遍。真实世界网络通常表现出的一种有趣的特点就是社区结构特征，就是在网络拓扑下组织而成的模块，它们通常被称作社区或者聚类[1-2]。

受最近出现的大数据的驱动，使用传统方法和算法的真实世界网络群已经几乎不可能在单独的机器中被处理[3]。为了应对这种情况，需要一种分散的并行计算模型来处理大型数据集，将数据集扩展到集群中的多台机器并进行处理[4-5]。

文献[6]提出一种凝聚层次聚类方法，该算法收敛地去最大化模块化功能，通过为网络中的每个节点分配不同的社区来启动该过程。通过不同级别的树形图切割为社区提供不同的分区，可以得到最佳的群落聚类。文献[7]提出分层凝聚优化方法，并且尝试优化网络分区的模块性。优化分两个步骤执行，且两个步骤迭代重复。该算法从属于其自己的社区的网络中的每个节点开始。这两个步骤反复重复，并且在模块增量时停止，因此可获得最大模块。此外，文献[8]提出一种基于短步行的节点相似性度量来捕获节点之间的结构相似性而不是模块性通过分层聚集来识别社区。首先将每个节点分配给自己的社区，并且每对社区的距离是被计算好的。社区根据它们的最小距离进行合并，该过程重复进行，并给出一个称为树状图的社区层次结构。

然而，传统的聚类算法是集中的(需要全局信息)，并且没有能力以并行(或分布式)的方式跨多个服务器处理数据。因此，提出一种新颖且实用的算法来解决聚类问题以及在大量间接网络中的社区检测问题。这里所提出的方法都假设需要将给定的网络结构划分为社区，使得每个节点属于一个社区，其主要创新点可总结如下：

(1) 提出一种基于网络加权Voronoi图的并行分散迭代社区聚类方法来提取大型网络的有效社区结构。该方法能够消除对网络全局架构的依赖，能够更有效地聚类网络。

(2) 大多数现有的社区检测算法不能在没有涉及惩罚的情况下对大型网络中的社区完成聚类，而结合网络加权Voronoi图的分散迭代社区聚类方法NWVD-DICCM可以通过聚合网络中的节点来有效地聚类大规模数据集，以便问题简化。

(3) 结合并行计算技术，将NWVD-DICCM方法的操作从串行过程转换为并行方法。实现NWVD-PDICCM流水线并行，并维护保持NWVD-DICCM的整体结构。NWVD-PDICCM也因为利用分布式存储器和在Spark框架下提取并行性的特性而具有更有效的聚类能力。

实验结果表明，NWVD-PDICCM可以与一系列计算机架构平台(例如PCs集群、多核分布存储服务器、GPUs等)共同运行，可以在最流行的Spark平台上实现并行操作，相比于文献[6]和文献[8]方法，大规模网络数据处理速度和准确度得到了显著提升。

1 本文方法

1.1 整体框架

NWVD-PDICCM方法包括两个工作方案：主工作者和从属聚类的工作者。主工作者程序在读取数据集时创建块，并将它们传递给从属聚类工作程序[9]。另一方面，从属聚类工作者的功能就是通过遍历自己的数据集并应用NWVD-PDICCM方法的第一阶段来识别局部社区。NWVD-PDICCM方法的流程如图1所示。

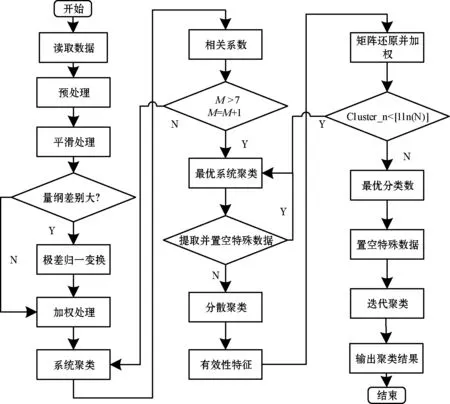
图1 网络加权Voronoi图的并行分散迭代社区聚类算法流程

1.2 网络加权Voronoi图的分散迭代社区聚类方法

网络加权Voronoi图分散迭代社区聚类方法主要包括三部分：首先是初始化数据以及特征向量提取，主要负责数据导入以及提取特征向量并进行预处理；其次是聚类算法部分，它是基于网络加权Voronoi图改进的分散迭代社区聚类算法的主体部分；最后是聚类结果部分，可以从中提取特殊数组[10]。

Voronoi 图是根据已知点集对平面施行的一种分割。其数学定义为：

给定平面上n个点构成的集合S={p1，p2，…，pn}，对每个生长点pi(i=1，2，…，n)，赋予非负实数权重λi，称V(pi，λi)为点pi的权重为λi的V区域。V(pi，λi)表达式如下：

(1)

式中:d(p，pi)为p与pi之间的Euclid距离。

图2给出了一个Voronoi图的例子，图中黑点为生长点，折线段为Voronoi边。

图2 Voronoi图示例

图3给出了一个加权Voronoi图的例子。由定义可知，Voronoi图是加权Voronoi图当所有生长点的权重相等时的特例。

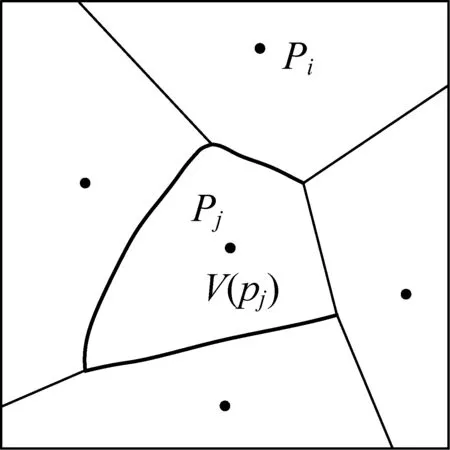
图3 加权Voronoi图示例

传统DICCM是一种基于随机游走和可达性的凝聚聚类算法，通过相邻之间的消息传播来实现。它有两个阶段，即局部聚类和网络缩减，并且以迭代方式运行。前一阶段用于为每个社区聚类定义起始节点[11]。缩减阶段则用于重建网络。网络加权Voronoi图的分散迭代社区聚类方法的流程如图4所示。

图4 网络加权Voronoi图的分散迭代社区聚类方法

每轮迭代过程包括随机选择一个节点作为起始点。 起始节点充当聚类头并通过向网络中的所有相邻节点发送消息(Msg)来通告自己。此消息包含三个参数：起始节点ID(OnID)，消息权重(Message weight，WMsg)和TTL。OnID表示的是消息发起者的节点ID。WMsg是消息携带的权重，表示从起始节点开始到达网络中任何节点的估计概率。TTL表示消息到期之前, 跳跃中的最大距离。值得注意的是，为了避免将起始点被分配给任何其他聚类，WMsg的起始点被设置为1。

考虑两个节点，起始点Oi及其相邻节点Vi，用于计算从起始点Oi发送到节点Vi的消息的权重的模型取决于Oi和Vi之间的边缘的权重。定义如下：

(2)

式中：Nbr表示第i个节点的相邻节点。

网络中的每个节点维护了有关起始ID的信息和它为每个起始者收到的消息的总权重。这个信息被表示为总消息权重。 当节点收到了来自相邻节点的信息后，它首先会更新消息总权重，并且随后检查TTL是否大于0。如果TTL大于0，则通过一个并行节点将消息转发给除了发送者以外的所有节点，从而降低消息的TTL。

从节点Vi发送到其相邻节点Oi的新消息(WMsg(Vi,Vk))的权重被定义为：

(3)

然而，如果TTL等于0或者WMsg值同预先定义的阈值相比减小的话，节点Vk处理消息并且停止下个阶段。

如果来自起始点的消息总权重大于指定的阈值，则节点加入最近的发起者Oi。如果不是这样的话，那些节点将保留为异常值并且不加入任何聚类[12]。

1.3 并行化

NWVD-PDICCM算法的核心思想是将数据集划分为块，然后迭代地重复以下三个阶段：聚类，重新聚类,重建。聚类阶段负责独立和并行地为每个块查找局部社区聚类。重新聚类阶段，从各个别的块中提取的局部聚类聚集起来，以找到整个网络的初始社区聚类。重建阶段涉及到基于初始社区聚类为每个数据块构建一个新的但更小的网络。通过上述三个阶段的该过程的每一个循环被称为迭代。这三个阶段迭代到旧的和新的社区聚类列表不再收敛。具体算法如下：

算法1NWVD-PDICCM

输入：底层网络图G、生存时间和阈值。

输出：作为G的最终划分的C社区。

重复

Outlier list all Nodes

//局部聚类阶段

While outlier list≠{}

Oi← Rand select (outlier list)

//随机选择一个节点作为发起人

OnId ← Oi

//发起人 ID

TTL ← time_to_live(time_to_live)

WMsg ← 1

Msg ← {OnId, TTL, WMsg}

While TTO≥0时

Total_weight(Oi, Vi)= sendmessages(G, Oi, OnId, TTL, Msg )

//Oi与其相邻节点之间的总权重(Vi)

TTL ← TTL-1

Oi← Vi

Msg ← {OnId, TTL, Total_weight(Oi, Vi)}

end while

for each Node Vi∈G

if Total_weight(Vi, OnID)≥ threshould then

C(Vi) Join the cluster lead by max onID

else

Remain outlier

end if

end

end

G = Aggregate(G, C)

if (C_current=C_previous)

//无成员变更

break；

return C

//返回C

end Algorithm

Function sendmessages (G, Oi, OnId, TTL, Msg)

for each Node Vi∈Nbr(Oi)

if Ni have seen message form onID before then

Total_weight(Vi,Oi) ← Total_weight(Vi,Oi)+WMsg

else

Total_weight(Vi, Oi) ← WMsg

end if

end

Return Total_weight(Vi, Oi)

end function

从属聚类工作程序并行运行，并将社区群集列表存储在其局部内存中。然而，由于每个从属聚类工作者有一部分数据并且不具有网络的全局知识，从而不同的从属聚类工作者可以将相同的节点聚类到不同的社区中。因此，当所有的块都被聚类并且已经识别了本地社区时，主工作者加载局部社区聚类列表以进行聚合。

重建阶段使用NWVD-PDICCM方法，由每个从属聚类工作者构建新网络。该新网络中两个节点之间连接的权重就是原始网络中两个相对应社区节点之间连接的总权重。 同一社区的节点之间的连接变为新网络中相应节点的自循环。 然后重复迭代，直到获得一组稳定的社区聚类(满足收敛条件)。

每个从属聚类工作者都拥有各自不可共享内存，并且在聚类阶段工作者之间没有通信。因此，每个从属群集工作者操作独立于其他操作，并且每个从属聚类工作者的操作是可以并行执行的[13]。对于聚类结果的评测指标，主要可定义为以下几种：

定义1聚类强度。这里给定一个网络集G=(V,E)，节点n=|V|，边m=|E|。在聚类阶段时，每个从属聚类工作者将这些节点聚集为C聚类，并将Vm节点分配给不同的社区。为了能找到适合Vm节点的最佳社区，提出的方案按照下面的两个步骤实施。

首先节点Vm从其每个相邻节点获得两组信息，即相邻节点的程度和它所属的集群，然后计算Vm与其相邻Vi之间的相邻吸引力，并且定义为：

(4)

式中：W(Vm,Vi)表示Vm与Vi之间的边缘的权重。

通过计算这些C聚类中的Vm对其相邻节点(Nbr Attraction)的吸引力之和，计算Vm所属的所有聚类(C)的Vm强度值，如下：

(5)

真正的社区结构(基本事实)以基准网络而著称，归一化互信度(NMI)用于将实验中获得的分区与LFR基准的基本事实进行比较，并以此来评估DICCM和PDICCM的性能。NMI指标通过评估检测到的和基本事实社区之间的对应程度来量化所提方法的准确性。

定义2归一化互信度。归一化互信度(NMI)是用信息理论概念比较两个分区的相似性度量，被广泛用于评估社区检测算法的准确性。

对于一个拥有两个分区n个节点网络，其划分分别为X={X1,X2,…,Xk}和Y={Y1,Y2,…,Yk}，其中X和Y分别代表了真实社区和查找社区，并且一个网络中两个划分X和Y的归一化互信度定义如下：

(6)

如果通过算法得到的查找分区与真实社区相同，则NMI取最大值1；如果找到的分区完全独立于真实分区，则NMI取0。

定义3模块化(Q)。模块化(Q)是衡量社区结构质量的重要指标，已成为社区检测的一种广泛接受的衡量标准。模块化表明，良好的聚类应该在模块内的节点之间具有大于预期的连接数，并且在不同模块中的节点之间的连接数量小于预期。模块化的价值越高，其社区力量就越好。

模块化优化算法的一般概念是通过搜索具有高模块性的网络的可能划分来检测模块化方面的最佳社区结构。模块化定义如下：

(7)

式中：Aij是相邻的基地元素；Ki是节点i的程度；δcicj是Kronecker三角洲符号，且其值为1。

2 参数设置与数据集

使用两个参数来评估本文方法：1) 生存时间(Time To Live,TTL)，允许消息在被丢弃之前传播的跳跃；2) 阈值，用于确定合并社区的难度。

2.1 生存时间

每条消息都有一个TTL区间，该区间以某个值T>0时启动，该值限制了消息转发的次数。实际上，需要谨慎选择合适的TTL值，因为TTL值小意味着消息在到达网络中的所有相关节点之前可能过期；TTL大意味着访问的节点多于所需的节点，从而增加了网络上的消息负载和算法的运行时间。因此，在这项工作中，建议在开始新的迭代之前重建网络。此外，基于现实世界的网络属性，据说来自应用的网络通常是小世界网络。简单来说，小世界概念描述了这样一个事实，也就是即使网络有许多节点，也存在连接网络中任何一对节点的相对少量的中间步骤。

2.2 阈 值

阈值是在过程开始时设置的参数，范围在0到1之间。如果节点从起始者Oi接收的消息的总权重等于或大于阈值，则节点能够加入由Oi主导的聚类。这就意味着阈值越高，节点合并到社区的可能性就越小。例如，将阈值设置为接近零时，将生成包含网络中所有节点的单个社区聚类。另一方面，将阈值设置为接近1时，将使每个节点位于其自己的聚类中。即低阈值产生大量小尺寸聚类；高阈值将产生较少数量的较大规模的聚类。因此，阈值对聚类精度以及检测到的聚类的大小具有重要影响。很显然，调整阈值可被视为控制所需社区的大小和数量的一种可能的实际补救措施。

选择合适的阈值是非常关键的，并且需要网络结构的先验知识。因此，提出一种自动计算阈值的数学模型。该模型利用网络的密度、大小和布局结构来找到最佳阈值。

式(8)-式(14)定义了为无向网络设置阈值的数学模型：

Thresholdvalue=avg_t+(t-1)×((1-C)×avg_t)

(8)

(9)

(10)

式中：i是主节点；j代表所有其他节点；A是邻接矩阵，若主节点i与其他节点j之间具有连通性，则Aij的值为1，否则，值为0；n是网络中节点的总数；t是迭代次数；Ki是节点i的度数；C是网络聚类系数。

(11)

式中：Li表示临近的节点i的边数。

完全连接的网络是n个节点的网络中的简单无向图，其中每对不同的节点通过唯一的边连接。基于图论，完全连通网络的网络聚类系数为1，每个节点的度数定义为：

Ki=n-1

(12)

因此，拥有n个节点的完整网络的总边数为：

(13)

计算得到完整的网络阈值：

(14)

值得一提的是，在每次迭代中，给定网络的阈值通过(t-1)×((1-C)×avg_t)逐步增加，如式(8)所示，使得密度较小的聚类彼此连接变得越来越困难。只有强关联的才能合并。 另外，最大阈值不能大于1。

2.3 实验数据集

为了分析社区检测算法在一系列网络规模上的效率，并且由于具有地面实况社区的真实网络的稀缺可用性，LFR基准被用于生成合成数据集。LFR基准模型是由Lancichinetti等为了生成与社区结构的现实世界网络非常相似的无向和未加权网络而提出的。LFR模型已成为评估社区检测算法性能的受欢迎的选择。

大多数现实生活网络已被定义和建模为无向和未加权/加权网络。提出LFR模型以解决实际网络的大多数特征，例如网络的大小和异构度分布。在LFR基准测试中，网络的节点度和每个社区的大小分别由具有指数γ和β的幂律分布控制[14]。然而，已经观察到真实世界图具有典型值为：2≤γ≤3,1≤β≤2这样的幂律度分布。

LFR模型提供一些其他参数来控制网络拓扑，其中包括节点数、最大度数和混合参数μ。 混合参数μ∈[0,1]，用于控制网络上的聚类内和聚类间边缘的分数。对于较小的μ值，将有少量边缘到达社区之外，这表明网络中有可用的清晰聚类。μ值越大，检测网络中的社区就越具有挑战性。LFR模式的代码已由作者公开[15-16]。

3 仿真实验与结果分析

3.1 环境设置

基于MATLAB平台实现NWVD-DICCM和NWVD-PDICCM，实验运行环境为4核CoreTMi5 7500 K CPU 4.00 GHz的Linux系统，可用运行内存为32 GB RAM。因为这些方法是随机初始化发起者，并且为了忽略本文方法中随机性的影响，每个结果的平均值超过200次运行。

使用LFR网络生成一组无向网络。默认基准参数值用作度分布和社区大小的指数的基准参数，即：γ=2，β=1。平均度和最大度分别为25和50。混合参数在0.10到0.75之间变化，节点数从500增加到5 000。

3.2 实验结果

3.2.1与并行核心数量相关的水平可伸缩性

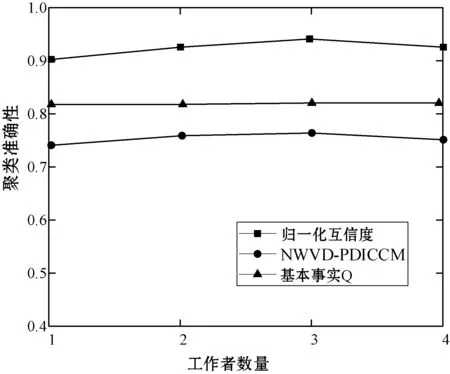
为了验证当更多工作者可用时，所提出的方法处理数据集的程度如何，实验中使用的网络中的节点数保持不变，工作者的数量从1到4不等。值得一提的是，如果工作者数量是1，算法只代表MLDICCM。图5所示为当节点数量恒定时，不同工作者数量对应的聚类准确性，n∈{600,1 200}。

(a) n=600

(1) 质量。由图5可知，所提方法显示出接近最佳值的良好可扩展性，其由平均模块性和NMI值表示。此外，使用多个工作程序来并行化算法不会对结果的准确性产生不利影响。因此，结果证明该算法是有效的并且能够以并行方式得到非常高质量的结果。具体地说，NWVD-PDICCM能够有效地利用多核架构。

(2) 消息复杂性。考虑到每个工作者交换消息的数量，图6所示为每个工作者处理器在每次迭代时交换消息的百分比。 正如在每次迭代中可以看到的，每个工作者生成几乎相同数量的消息，这可以通过以下事实来澄清：数据已在工作者中平均分配，因此每个工作者必须处理相同大小的数据。在每次迭代时，主工作者必须等到所有从属工作者完成他们的过程。 因此，将数据平均分配给工作者可以显著减少等待最慢的机器的工作者返回数据所需的预期时间。

图6 节点数量为1 200时，工作者从2到4变化过程中，每次迭代交换的消息数量

3.2.2增长的网络大小的聚类结果

为了证明被可扩展性影响的性能，节点数量从500线性增加到5 000，工作者数量保持恒定在1和3。所有其他参数和因素保持与先前评估相同。

对于更深入的分析，图7显示了每次迭代过程中消息交换的平均百分比。从数据中可以很容易地看出，当每个节点在其自己的聚类中时，算法的数据交换在迭代的第一阶段要大得多。在2到3次初始迭代之后，大多数节点都有其聚类标签，并且算法已将属于同一聚类的节点合并为一个节点。从表1中的主工作者(主工)和从属工作者(从工)之间交换消息的百分比也可以清楚地看到，通信成本可以忽略不计。然而，相比主工与从工之间信息交换成本，从工中局部信息交换的成本明显较高，这部分是算法的时间消耗主体。

图7 对于网络规模1 200，每次迭代交换的消息的平均百分比与核心数量从1到4个工作者的变化

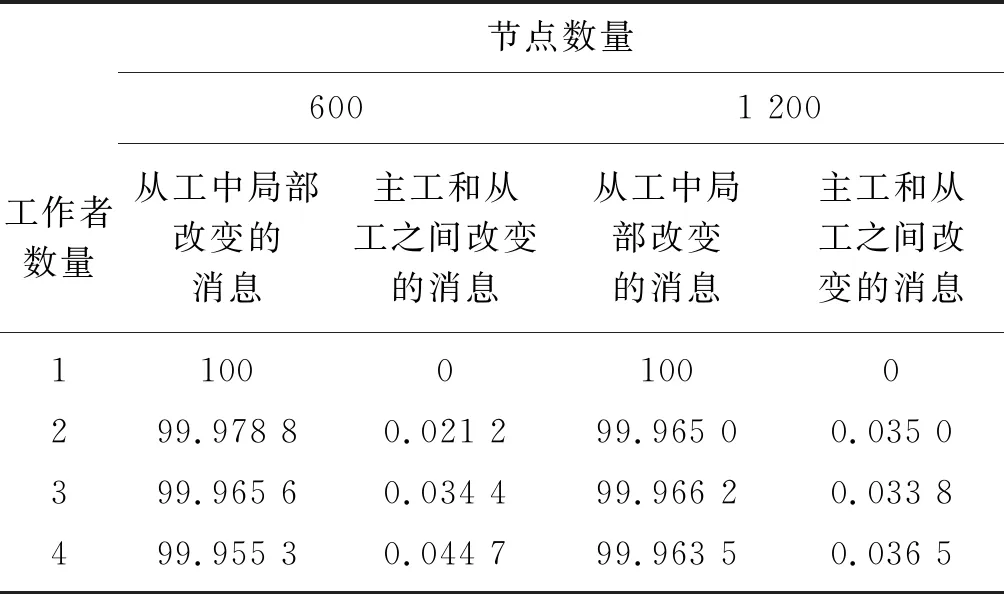
表1 与主机进行本地交换的消息以及主机和主机之间交换的消息进行比较 %

(1) 质量。由NWVD-DICCM和NWVD-PDICCM获得的解的模块性值如图8所示。可以看出，NWVD-DICCM和NWVD-PDICCM的性能始终良好且接近最佳值，NMI平均大于0.90。

图8 节点数量对聚类准确性的影响

(2) 性能的可重复性评估。为了进一步研究NWVD-DICCM和NWVD-PDICCM在随机数据分区和初始化中随机启动时产生一致结果的能力，聚类结果的标准偏差被测量了，其中NWVD-DICCM和NWVD-PDICCM每次运行100次，使用不同的随机数据分区和算法初始化。在不同节点数量情况下，记录NMI与网络模块的标准偏差，如图9所示。

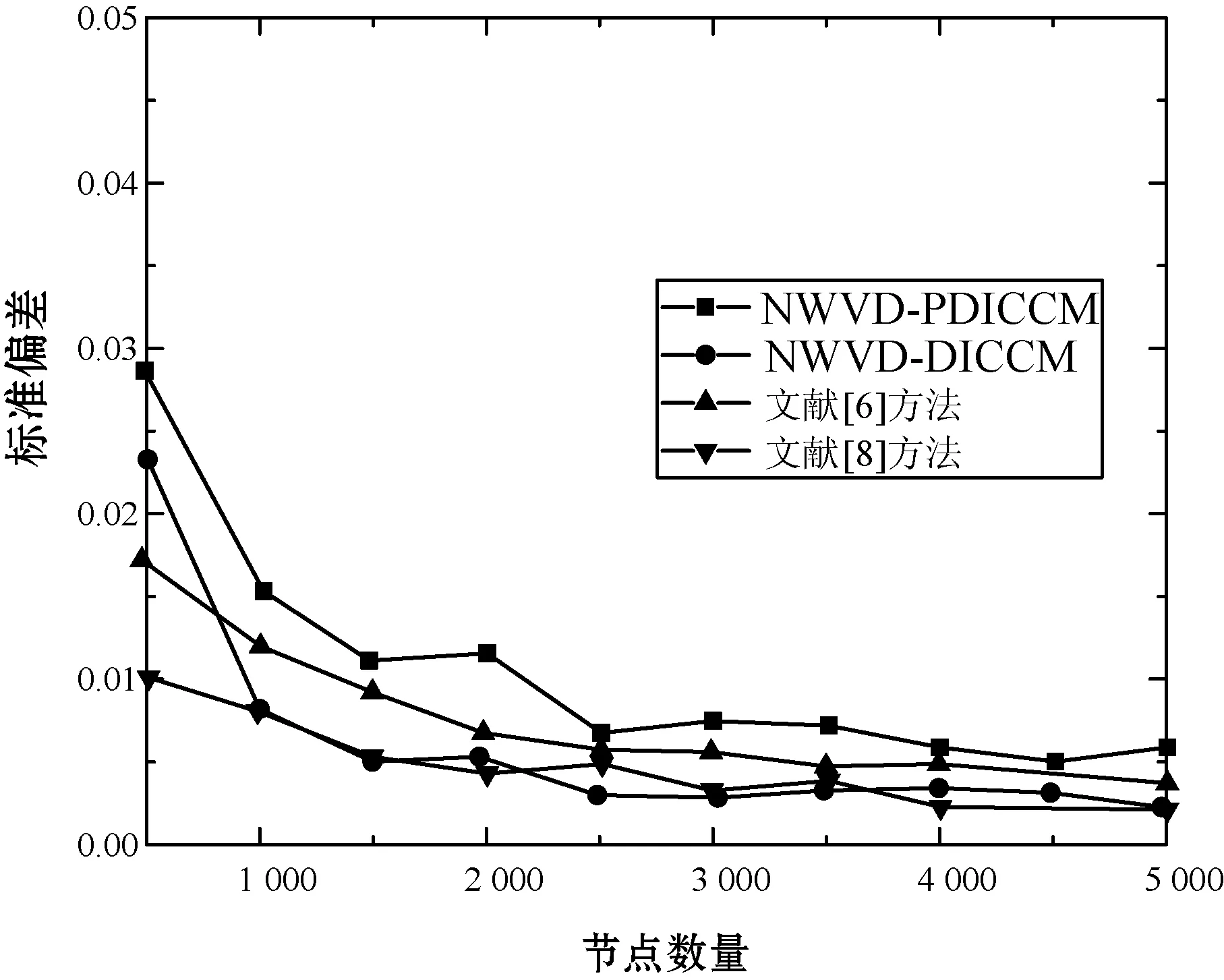
图9 节点数量对标准偏差的影响

3.2.3使用混合参数的聚类性能评估

当社区结构被高度增长的社区内部连接(LFR基准的μ值具有较高值时发生)削弱时，为了研究NWVD-DICCM和NWVD-PDICCM的社区聚类能力，将混合参数设定在0至0.8之间，并保持节点数恒定，n∈{1 000}，记录混合参数μ对几种算法聚类准确性的影响，如图10所示。可以清楚地看到，当混合网络参数低于0.7时，NWVD-DICCM和NWVD-PDICCM获得的准确性均高于其他2种对比方法，然而，当混合网络参数继续增大时，NWVD-DICCM的准确性低于文献[6]方法。分析原因可知，当混合网络参数值较低时，网络中明确定义的社区结构，大部分边缘节点可落在社区内，因此NWVD-DICCM和NWVD-PDICCM具有较高的聚类准确性。当网络参数值较大时，边缘节点很难落在社区内，一定程度上影响NWVD-DICCM的聚类效果。通过引入网络加权Voronoi图可以有效解决该问题，因此，改进后的NWVD-PDICCM方法可以一直保持较高的聚类准确性。

图10 混合参数μ对聚类准确性的影响

4 结 语

本文提出一种基于网络加权Voronoi图的并行分散迭代社区聚类方法(NWVD-DICCM)及其并行版本(NWVD-PDICCM)，以提取大型网络的有效社区结构。本文方法的一个重要特性是它们能够在没有全局网络拓扑知识的情况下从整个网络中识别最佳社区聚类。本文方法解决了围绕处理大数据集的计算需求的问题。它们通过以并行方式处理多个块，最佳地利用现代多核系统的硬件功能，从而加快执行速度。此外，当数据大小超出单个机器的处理能力时出现可扩展性问题时，基于Spark计算平台的建议分布式方法将有助于解决这个问题。最后，使用具有基本事实的社区的合成网络来测试和分析这些方法的有效性和复杂性。

现实世界的网络通常不包含完美的社区，实际上节点可能同时属于多个社区。识别这种重叠社区对于理解现实世界网络的结构和功能至关重要。因此，未来主要方向是扩展所提出的方法以能够检测出这种模糊社区。此外，本文只考虑了无向网络，对于有向网络则需要进一步深化研究。