基于FFT和DTFT的指数衰减复正弦信号参数估计算法
2021-03-16刘春华齐国清
王 鸿 刘春华 齐国清
(大连海事大学信息科学技术学院 辽宁 大连 116026)
0 引 言
噪声背景中的指数衰减复正弦信号参数估计技术是数字信号处理领域中的一个经典课题,广泛应用于低频机械光谱学[1]、线性系统识别[2]、核磁共振波谱分析[3]等领域。为提高该类信号频率和衰减因子的估计精度,国内外众多学者做了大量研究,主要分为频域和时域两方面[4]。许多时域算法都以奇异值分解为基础,虽然参数估计精度较高,但计算量大,效率不高[5]。为提高指数衰减复正弦信号参数估计算法的运算速度及抗噪声性能,本文从频域角度进行研究。
由于FFT得到的是离散频率值,信号频率可表示为f0=(m+δ)Δf。其中:m是幅度最大谱线对应的离散频率索引值;δ是信号频率与幅度最大谱线位置的相对频率偏差,且δ∈[-0.5,0.5];Δf为频率分辨率[6]。基于FFT插值的指数衰减复正弦信号参数估计算法可分为粗估计和精估计两个步骤,而各算法的差异仅体现在精估计中[7]。文献[8]提出了利用信号FFT离散频谱主瓣内幅度最大谱线和次大谱线得到估计频率和衰减因子的算法,该算法简单、计算量小,但当信号实际频率与幅度最大谱线对应的频率接近(δ接近0)时,次大谱线幅度很小、易受噪声影响导致频率和衰减因子估计的误差增大。文献[3]提出Bertocco-Yoshida一阶离散傅里叶插值算法(BY1),该算法使用了FFT离散频谱中最大的三根谱线,在低信噪比和FFT点数较少时具有一定优势,但整体估计精度不高。利用FFT得到的信号x(n)的离散频谱X(k)只在离散频率索引值k取整数值时有值,文献[9]将k推广到非整数值的情况,提出了一种Aboutanios-Mulgrew算法(A&M)。k=m时,X(m)为幅度最大谱线,该算法利用x(n)的DTFT(连续时间傅里叶变换)抽样得到X(m)位置+0.5Δf和-0.5Δf处的两根离散谱线来估计频率和衰减因子。文献[10]提出了一种基于指数衰减窗的改进A&M算法,但利用原信号衰减因子的估计值选择最优窗函数e-γn/fs的系数γ的公式是由大量实验数据拟合得到,难以适用于所有的应用场合。文献[11]利用文献[10]算法的原理估计多频率指数衰减复正弦信号参数,但存在相同的缺点。针对指数衰减复正弦信号的参数估计问题,A&M算法在现有算法中性能最好,但该算法只讨论了当i=0.5这一特定值时,原信号的DTFT在X(m)位置+iΔf和-iΔf处的两根离散谱线对信号参数估计性能的影响。对于恒定幅度正弦信号,文献[12]提出了一种结合FFT和DTFT利用X(m)及其+iΔf和-iΔf位置处的两根离散谱线估计信号频率的算法。为尽量避免利用幅度很小的离散频谱,文中约定i∈(0,1],并发现当i<0.5时,算法性能接近CRLB,且随i的增加,性能基本不变;当i≥0.5时,随着i的增加,性能逐渐变差。与利用信号补零达到相同效果的FFT类算法[13-14]相比,文献[12]算法的计算量与i的取值无关;而信号补零后长度与i的倒数成正比,当i较小时,补零类算法的计算量是难以接受的。对于恒定幅度正弦信号频率的估计,文献[12]提出的方法可达到最优效果。但是,对于指数衰减复正弦信号,通过实验发现,并不能直接应用文献[12]算法进行参数估计,尤其当衰减因子较大时估计性能很差。因此,借鉴文献[12]算法的思路,本文提出一种结合FFT和DTFT估计指数衰减复正弦信号频率和衰减因子的三谱线插值算法,分析了i对算法性能的影响并给出了选择i的建议。
1 算法原理
加性高斯白噪声背景下,观测信号序列表示为:
x(n)=s(n)+u(n)
(1)
s(n)=b0e-αn/fsexp[j(2πf0n/fs+θ0)]
(2)
式中:n=0,1,…,N-1;s(n)为指数衰减复正弦信号;f0、α、b0、θ0分别为频率、衰减因子、幅度和初始相位;u(n)为复高斯白噪声,均值为0,方差为σ2;fs为采样频率。
对s(n)做N点FFT,搜索幅度最大谱线的位置m,FFT幅度最大谱线可表示为:
(3)
s(n)经DTFT后,计算s(n)的DTFT在(m+i)Δf和(m-i)Δf处离散抽样,并用S±i表示,约定i∈(0,1]。
S±i=S(ejω)|ω0=DTFT[s(n)]|ω0=
(4)
式中:ω=2πf/fs为圆周频率;ω0为抽样点处的离散频率:
ω0=2π(m±i)Δf/fs=2π(m±i)/N
根据式(4)可得Si和S-i的表达式为:
(5)
(6)
用复数变量Z表示相对频率偏差δ和衰减因子α,即Z=e-α/fsej2πδ/N,并计算以下比值:
(7)
(8)
联立式(7)、式(8),得到Z与S0、Si、S-i关系为:
(9)
根据Z的定义,可得δ和α的估计公式为:
(10)
(11)
式中:argZ为取Z的相角;ln|Z|为取|Z|的幅值。因此,信号频率f0的估计公式可表示为:
(12)
2 算法精度分析
在噪声环境中,x(n)的N点FFT为:
X(k)=S(k)+U(k)k=0,1,…,N-1
(13)
当k=m时,幅度最大谱线为X(m),记为X0=S0+U0;x(n)的DTFT抽样后得到X(m+i)和X(m-i),分别记为Xi=Si+Ui和X-i=S-i+U-i。
2.1 噪声系数的统计性质
复高斯白噪声频域系数U0、Ui、U-i的方差皆为Nσ2,但当i为非整数时,U0、Ui、U-i两两间的协方差不再为0[10]。按协方差定义整理得到公式如下:
(14)
(15)
同理,可得到其他两两系数间的协方差公式。
2.2 频率和衰减因子估计精度分析
令a=e-j2πi-1,b=j2sin2πi,c=ej2πi-1,d=ej2πi/N,e1=e-j2πi/N。式(9)可重写为:
(16)

(17)
替换相关变量后,可得:
(18)
对式(18)进行一阶泰勒级数展开并省去高次项:
(19)

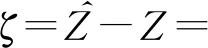
(20)

ln(Z)=-α/fs+j2πδ/N
(21)
(22)
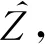
(23)

联立式(22)、式(23)整理得到:
(24)
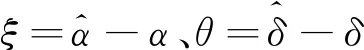

(25)
利用式(14)和式(15)推出E[HH*]的表达式为:
E[HH*]=(|a(1-Zd)|2+|b(1-Z)|2+
|c(1-Ze1)|2)Nσ2+
(26)
根据ξ和θ的表达式可推出:
(27)
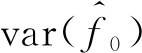
(28)
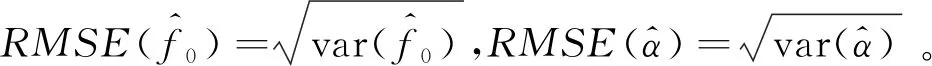
3 迭代策略的应用
3.1 非迭代情况下的算法性能分析
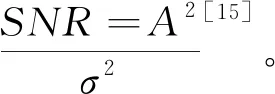
本节分析i分别为0.1、0.3、0.5、0.7、0.9时,f0和α估计的归一化均方根误差随相对频率偏差δ变化的情况。参数设为:α=5,fs=51.2 kHz,N=512,f0=(N/4+δ)fs/N,则f0∈[12.75,12.85] kHz,θ0随机变化,SNR=37 dB,结果如图1和图2所示。

图1 f0估计的归一化均方根误差随δ变化的仿真结果

图2 α估计的归一化均方根误差随δ变化的仿真结果
仿真结果表明,当i一定时,f0和α估计的归一化均方根误差随|δ|增加而增加,故可借鉴文献[12]的迭代策略,提高参数的估计精度。
3.2 迭代步骤
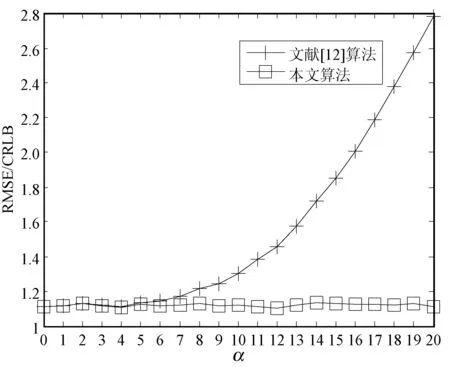
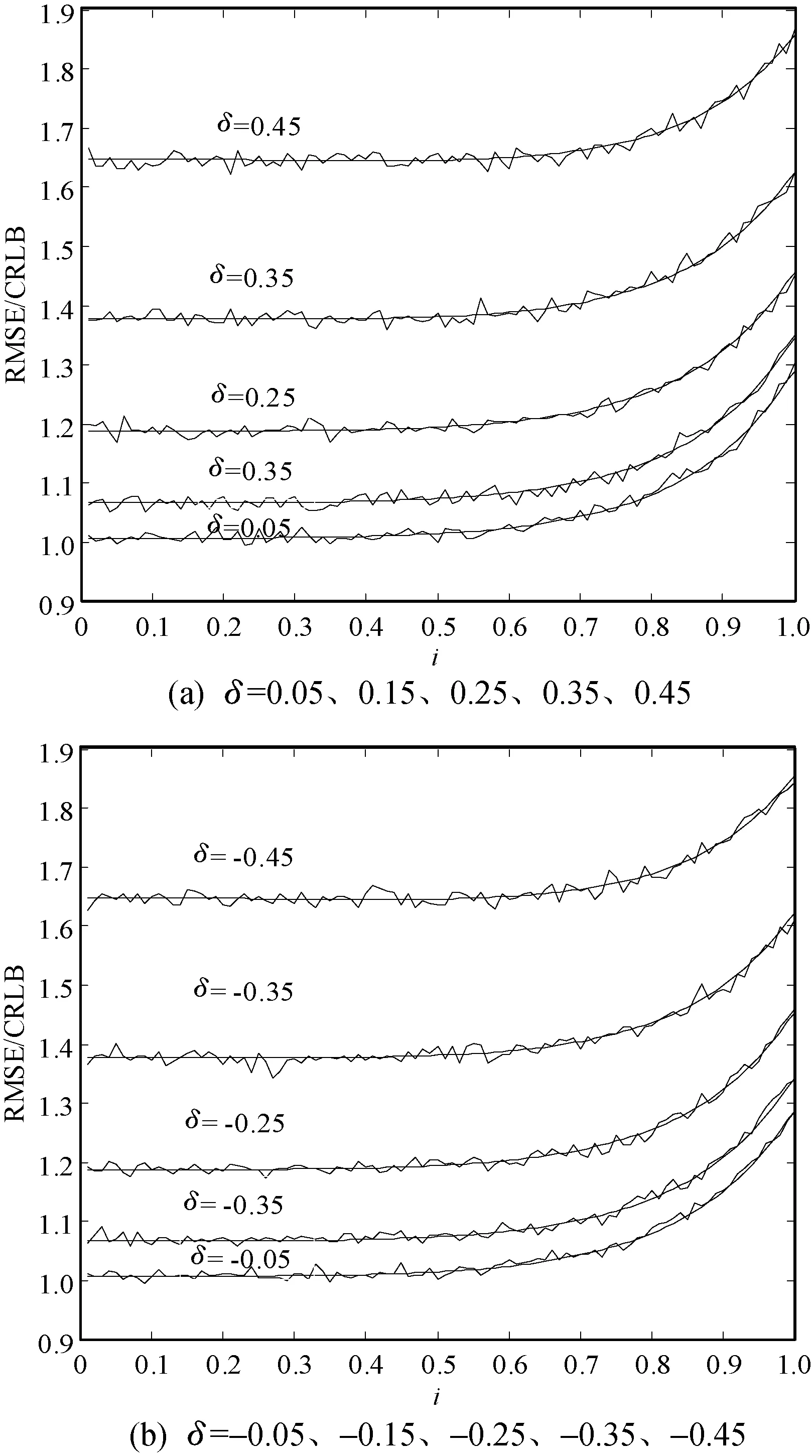
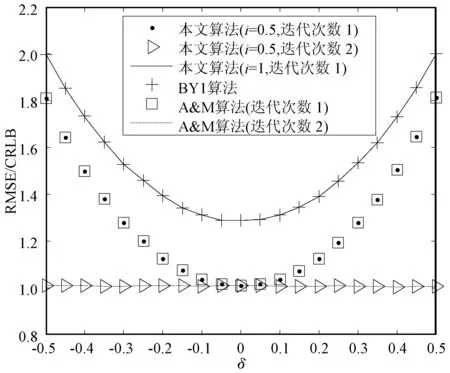
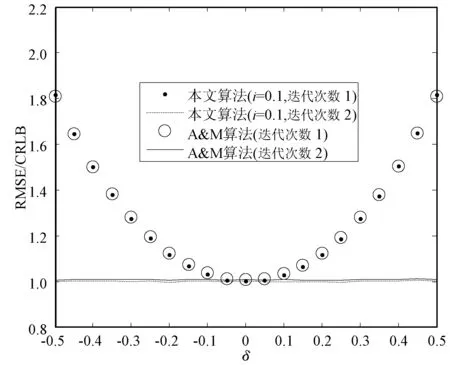
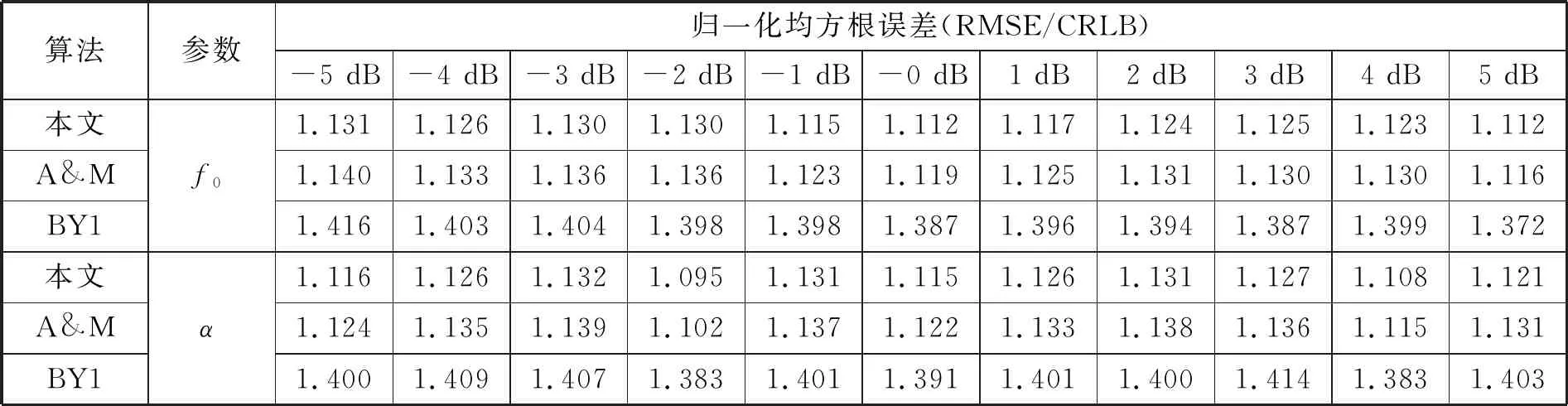
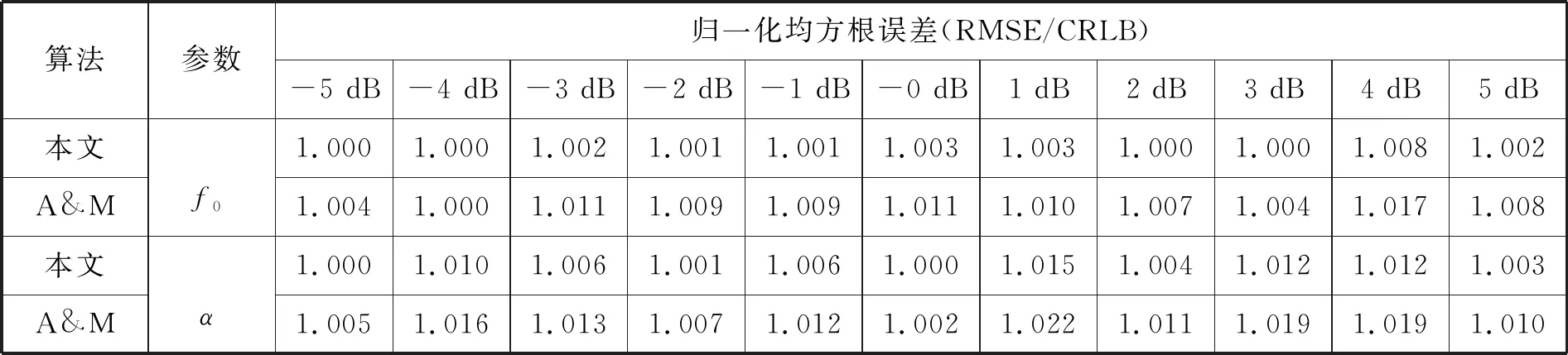
从图1和图2中也可以看出当0 2) 对x(n)进行FFT变换,找到m,并得到X0。 3) 信号x(n)经DTFT后,在连续频谱位置m+p处离散抽样,并计算X0.1和X-0.1。 (29) (30) 为验证本文算法性能,本节通过计算机Monte Carlo模拟实验进行仿真。 文献[12]算法、BY1算法和A&M算法估计δ和α的表达式如下所示(信号模型以式(1)为准,BY1算法和A&M算法的公式有细微调整)。 文献[12]算法: BY1算法[3]: A&M的迭代算法[9]: 并依次计算: (1) 仿真实验1。图3给出了本文算法和文献[12]算法的f0估计性能随α变化的关系曲线。参数设为:fs=51.2 kHz,N=512,i=0.2,δ=0.2,f0=(N/32+δ)fs/N,则f0=1.62 kHz,SNR=37 dB,θ0随机变化,α在[0,20]内变化,步进1,迭代次数均为1。 图3 f0估计的归一化均方根误差随α变化的仿真结果对比 仿真结果表明,α较大时,直接应用文献[12]算法估计指数衰减正弦信号参数的性能很差,而本文算法是基于指数衰减的信号模型进行推导的,即使在α较高的情况下,算法性能几乎不受影响。 (2) 仿真实验2。图4和图5给出了δ分别为0.05、0.15、0.25、0.35、0.45以及-0.05、-0.15、-0.25、-0.35、-0.45时,本文算法的f0和α估计性能随i变化的关系曲线。参数设为:α=5,fs=51.2 kHz,N=512,SNR=37 dB,f0=(N/4+δ)fs/N,则f0∈[12.75,12.85] kHz,θ0随机变化,i在[0.01,1]内变化,步进0.01,迭代次数为1。 图4 f0估计的归一化均方根误差随i变化的仿真结果 图5 α估计的归一化均方根误差随i变化的仿真结果 可以看出f0和α估计的理论曲线和仿真曲线吻合,归一化均方根误差随|δ|的增大而增大。若δ为定值,当i<0.5时,f0和α估计的归一化均方根误差基本不变;当i≥0.5时,归一化均方根误差随i的增加而增加。原因是当i<0.5时,S0的幅值大于Si、S-i的幅值,且Si、S-i的幅值相对较大,不易受噪声影响。因此,在实际应用中,辅助谱线应当选择位于幅度最大谱线位置+(i<0.5)Δf和-(i<0.5)Δf处的两根离散谱线。 (3) 仿真实验3。参数设置为:α=5,fs=51.2 kHz,N=512,θ0随机,f0=(N/4+δ)fs/N,则f0∈[12.75,12.85] kHz,SNR=37 dB。 图6和图7给出了本文算法、BY1算法和A&M算法的f0和α估计性能随δ变化的关系曲线。当i=0.5时,根据式(9)可知,本文算法只用了S0.5、S-0.5两根离散谱线,从图中可以看出,本文算法(i=0.5)性能和A&M算法基本一致。当i=1时,本文算法采用了S0、S1、S-1三根离散谱线,本文算法(i=1)性能与BY1算法基本一致。这里i的取值只是为了方便与另外两种算法进行比较。 图6 三种算法的f0估计性能随δ变化的仿真结果对比 图7 三种算法的α估计性能随δ变化的仿真结果对比 图8和图9给出了本文算法(i=0.1)和A&M算法的f0和α估计性能随δ变化的关系曲线。实际上,当0 图8 两种算法的f0估计性能随δ变化的仿真结果对比 图9 两种算法的α估计性能随δ变化的仿真结果对比 (4) 仿真实验4。实验4研究了不同信噪比下,本文算法、BY1算法和A&M算法的f0和α估计性能。参数设为:α=5,N=512,θ0随机,fs=51.2 kHz,δ=0.2,i=0.1,f0=(N/4+δ)fs/N,则f0=12.82 kHz,信噪比步进1 dB。 实验结果如表1和表2所示。在表1中,本文算法和A&M算法迭代1次;在表2中,本文算法和A&M算法迭代2次。实验结果表明,在不同信噪比条件下,本文算法频率和衰减因子估计的归一化均方根误差比A&M算法和BY1算法的更小;经过两次迭代后,本文算法的f0和α估计性能更接近CRLB。 表1 δ=0.2时三种算法的f0和α估计性能对比(迭代1次) 表2 δ=0.2时两种算法的f0和α估计性能对比(迭代2次) 本文探讨了加性高斯白噪声环境中,指数衰减复正弦信号频率和衰减因子的估计问题,提出一种结合FFT和DTFT的三谱线插值估计算法。算法将辅助谱线的选择推广到了幅度最大谱线位置+iΔf和-iΔf处两根离散谱线;推导了频率和衰减因子的估计公式和理论均方根误差公式;分析了i取值对算法性能的影响。仿真结果表明,当i=0.5时,本文算法与A&M算法性能基本一致;当i=1时,本文算法(迭代1次)与BY1算法性能基本一致;当i的取值小于0.5时,本文算法性能优于现有性能最好的方法,接近克拉美罗下界。在实际应用中,为取得更好的参数估计性能,应选择最大幅度谱线位置+(i<0.5)Δf和-(i<0.5)Δf处的两根辅助谱线参与算法估计。



4 仿真实验

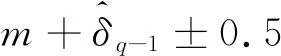
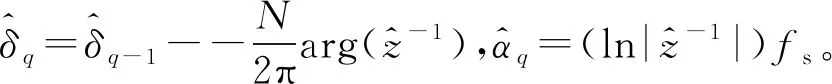




5 结 语
