一种云间合作博弈资源提供方法

董 玮

(吉林开放大学 吉林 长春 130022)

0 引 言

云计算技术的目标是通过利用虚拟化技术(Virtualized Technology)将分布于互联网上的各种类型的IT资源最终整合为可扩展的大规模资源池，然后利用互联网作为载体向用户方提供软件服务、平台服务及基础设施服务[1-2]。鉴于广大云用户的需求拥有很强的动态可变性，尤其针对特定型的数据密集的计算需求，这类任务对于计算资源的需求量的激增会导致单个云资源提供者的资源提供环境无法满足用户需求，导致资源提供方不得不改变现有的服务提供商业模式，进而寻找改善其动态资源服务能力的可扩展方法。当前，操作性较强的适用方法是多个云资源提供者之间可以建立合作关系，通过建立资源提供方联盟的模式，进一步完善异构资源在用户需求上的优化配置。

文献[3-4]较早地研究了多个云资源提供者之间建立云间联盟的需求，但是没有设计云间联盟的有效形成机制。文献[5]建立了一种局部云与远程云的联盟构建模型，其运用场景是当局部云无法满足用户需求时，代理可以向远程云租购资源，但该联盟构建机制没有论证资源方的联盟形成动机。文献[6]设计了一种基于联盟个体利益最大化的联盟形成决策方法，单个云资源提供者可以对是否与公有云提供者形成联盟给出依据，但该方法并没有考虑不同类型不同利益共同体的云资源对联盟形成决策的影响，同时也没有考虑不同类型的虚拟机实例需求和异构资源间的映射与调度问题。文献[7]基于公有云与私有云的混合环境，设计了一种基于二进制整数规划的最小化代价任务调度算法，但算法仅优化了私有云的资源利用率，没有给出混合云的最优解。文献[8]设计一种基于博弈式博弈的云资源调与分配方法，通过建立资源提供商之间的合作关系，能够实现合作各方的总体利益最大化。文献[9]基于效益博弈理论，设计了一种动态且可调合的云计算资源分配算法，构建了一种效益博弈模型，并利用时间矩阵和费用矩阵作为衡量指标，同时求解了博弈解。文献[10]基于服务质量需求设计了一种资源分配博弈方法，方法将云资源分配过程中的服务质量保证问题建模为合作博弈，同时证明了该问题存在帕累托最优解。然而，上述研究工作都忽视了以协作方式产生资源联盟的稳定性。

本文将所有参与的云资源提供者的决策动机都考虑进来，综合所有因素对是否形成联盟资源作出决策，为了实现资源联盟的总体利益最大化，提出了一种云联盟形成博弈算法。

1 系统模型

1.1 云资源提供系统模型

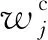
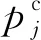
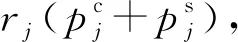
1.2 云联盟模型

将云联盟形成问题建立为一个联盟博弈模型[11]，可将联盟博弈定义为(I,v)，其中：I表示博弈者集合，即云资源提供者；v表示在F⊆I上的联盟博弈的特征函数，特征函数为一个实数值函数，满足v:F→R+，v(∅)=0。

每个子集F⊆I表示一个联盟，若所有云资源提供者构成一个联盟，则称之为大联盟。一个联盟F拥有一个价值，该价值由特征函数v(F)定义。同时，v(F)代表的是当F中的云资源提供者协作组成集群时所能获得的利益，定义为：

(1)

由于对于给定的联盟F而言，其目标是最大化其利益，可将云联盟利益最大化问题形式化为一个整数规划问题，目标函数即：

(2)

约束条件为：

(3)

(4)

(5)

(6)

(7)

(8)

式(2)代表v(F)，即联盟F中云资源提供者可获得的利益，等于用户支付与资源代价之差。式(3)确保云资源提供者分配至用户的内核数量小于其可用内核数量；式(4)确保云资源提供者分配至用户的存储量小于其可用存储量；式(5)确保云资源提供者分配至用户的每种类型VM实例的内核数量等于用户请求该VM实例的内核数量；式(6)确保云资源提供者分配至用户的每种类型VM实例的存储量等于用户请求该VM实例的存储量；式(7)确保联盟中的每个云资源提供者至少贡献一种资源类型。以上约束条件使得云资源提供者可以向联盟贡献资源。式(8)代表决策变量是整数。

定义ψCi(F)为联盟F中云资源提供者Ci所能获得的利益分配量，该值为标准化Banzhaf值给出。Banzhaf值[12]是在考虑博弈者能力的条件对于联盟利益的一种分割方式。本文将这种博弈者能力定义为云资源提供者的市场占有率。若在所有可能联盟中，一个云资源提供者可贡献的资源越多，则其利益分配也将越多。

2 云联盟形成机制

2.1 云联盟形成模型

云联盟博弈的核心可能为空。若大联盟无法形成，即需要形成独立且不相互的联盟形式。联盟博弈形成理论即是研究在大联盟无法形成时博弈中联盟结构的理论。联盟形成讨论的即是将所有博弈参与者分割为不相交的集合。一种联盟结构FS={F1,F2,…,Fh}构成对于云资源提供者集合I的一种分割形式，每个云资源提供者准确地成为一个联盟中的成员，即对于所有的i和j，当i≠j时，有Fi∩Fj=∅，且∪Fi=I。定义Q为所有可能联盟结构的集合，寻找最优联盟结构为NP难问题。

将云联盟形成问题建模为云资源提供者在联盟结构上拥有偏好的享乐博弈。

定义1享乐博弈[13]。享乐博弈即为(I,≥)，≥i表示在Qi上的反射完全可传递二进制关系，Qi表示包含Ci的联盟I的集合。

定义≥i表示云资源提供者Ci的联盟偏好关系，该关系允许Ci比较两个联盟结构，并指出该云资源提供者对成为其中一个联盟成员的偏好。若A≥iB，则表明Ci偏好于成为联盟A的一个成员，而不偏好于成为联盟B的成员，或至少对于两个联盟拥有相同偏好。此外，若A>iB表明Ci严格偏好于成员联盟A的一个成员，而不成为B的成员。

为了将云联盟形成问题建立为享乐博弈模型，需要定义联盟的偏好关系。对于所有的Ci∈I和所有F，F′∈Qi，定义≥i为：

F≥iF′⟹v(F)≥v(F′)

(9)

式(9)表明一个云资源提供者将偏好于选择给予更高利益分配的联盟结构。利用这种偏好关系，每个云资源提供者可以在所有可能形成的联盟结构中评估其成为其中一个联盟成员的偏好。

为了找到一个相比其他联盟结构更加偏好的联盟，定义两种比较关系分别为合并关系Δm和分裂比较Δs，具体如下：

{F∪F′}Δm{F,F′}⟺

{∀Ci∈F;{F∪F′}>iFand

∀Cj∈F′;{F∪F′}>jF′}

(10)

{F,F′}Δs{F∪F′}⟺

{∃Ci∈F;F≥i{F∪F′} or

(11)

式(10)表明若联盟{F∪F′}获得的利益大于F和F′获得的利益，联盟{F∪F′}比较两个不相互的联盟{F,F′}将获得选择偏好，如此所有资源提供者可以改进其总利益。式(11)表明如果至少一个联盟可以在不影响其他博弈者的情况下维持相同利益或增加其成员的利益，则{F,F′}将获得比{F∪F′}更大的选择偏好。

利用定义的比较关系，可以提出基于以下两种规则进行云资源联盟形成机制[14]：

合并规则：若{F∪F′}Δm{F,F′}，则需合并联盟集合{F,F′}；

分裂规则：若{F,F′}Δs{F∪F′}，则需分裂联盟{F∪F′}。

如果所有云资源提供者可以通过合并规则严格改进其总利益，则联盟决定合并。因此，若对于参与者是有利的，合并将在云资源提供者间达成共识。

如前所述，最终所形成的联盟才提供请求的VM实例。因此，其他的联盟形式并不重要。原因在于不在最终联盟结构中的其他云资源提供者可再次参与其他请求的联盟形成和资源提供过程。因此，仅当至少一个子联盟可严格改进其资源提供者的总体利益时，联盟结构可决定进行分裂。在这种分裂规则下，其他子联盟的利益可能降低。分裂规则可视为一种自私的联盟决策，并不考虑分裂过程对于其他联盟形式的影响。

通过合并/分裂过程，可能的联盟形式被访问，其价值被计算。基于该价值，定义云资源提供者Ci的估计Banzhaf值为：

(12)

式中：V表示所有可遍历访问的联盟集合；λ表示包含Ci的所访问的联盟总数，λ=2m-1-β，β表示没有被访问的联盟数量。估计Banzhaf值根据在合并与分裂过程中已被访问的联盟的价值进行计算，其标准化估计Banzhaf值为：

(13)

每个成员Ci可从大联盟结构中获得的利益计算为：

ψCi(I)=ξCi(I)v(I)

(14)

支付向量ψ(I)=(ψC1(I),ψC2(I),…,ψCm(I))给出大联盟的利益分割方式。定义对于云资源提供者Ci∈F获得的利益ψCi(F)为：

(15)

在联盟进行合并与分裂过程中，根据联盟形式估计每个云资源提供者的Banzhaf值，即联盟所获利益将依据联盟中成员的能力在所参与的资源提供者间进行正比例分配。

2.2 云联盟形成算法

算法1给出了云联盟形成算法CFFM。算法利用分支限界法求解每个联盟中任务调度的线性规划问题，进而找到资源分配和联盟的利益分配方案。算法定义B&B-VM-ALLOCATION(Fi)为实现求解联盟Fi的线性规划问题的分支限界法的功能。

算法1云联盟形成算法

1. receive requestR

//接收来自用户的VM服务请求

2.FS={{C1},{C2},…,{Cm}}

//初始联盟结构设置

3. calculatev(Fi) forFi∈FS

//计算联盟价值

4.repeat

5.stop←TURE

6.forallFi,Fj∈FS,i≠j,do

7.visited[Fi][Fj]←FALSE

//初始化联盟对为未遍历

8.endfor

9. {联盟合并过程开始}

10. repeat

11.flag←TURE

12. randomly selectFi,Fj∈FSfor whichvisited[Fi][Fj]=FALSE,i≠j

//随机选择联盟对进行合并尝试

13.visited[Fi][Fj]←TRUE

//设置联盟对已被遍历

14. B&B-VM-ALLOCATION(Fi∪Fj){Allocate VMs usingFi∪Fj}

//分支限界法求解该联盟上的虚拟机分配问题

15.ifFi∪FjΔm{Fi,Fj} then

//满足联盟合并规则

16.Fi←Fi∪Fj{mergeFiandFj}

//联盟合并

17.Fj←∅ {Fjis removed fromFS}

//更新联盟

18.forallFk∈FS,k≠i,do

19.visited[Fi][Fk]←FALSE

20.endfor

21.endif

22.forallFi,Fj∈FS,i≠j,do

//在联盟结构中的所有联盟对上进行遍历

23.ifnotvisited[Fi][Fj]then

24.flag←FALSE

//设置终止标识

25.endif

26.endfor

27.until(|FS|=1) or (flag=TRUE)

//合并终止条件

28. {联盟分裂过程开始}

29.forallFi∈FSwhere |Fi|>1do

//在所成员数大于1的联盟上进行遍历

30.forallpartitions{Fi,Fk} ofFi,whereFi=Fi∪Fk,Fi∩Fk=∅do

//对所有没有交集的联盟分裂形式进行遍历

31. B&B-VM-ALLOCATION(Fj){Allocate VMs useFj}

//分支限界法求解该联盟上的虚拟机分配问题

32. B&B-VM-ALLOCATION(Fk){AllocateVMs useFk}

//分支限界法求解该联盟上的虚拟机分配问题

33.if{Fj,Fk}ΔsFithen

//满足联盟分裂规则

34.Fi←Fj{that isFS=FSFi}

//更新联盟

35.FS=FS∪Fk

//更新联盟结构

36.stop←FALSE

//设置终止标识

37. break(one split occurs; not check other splits)

//跳出分裂过程

38.endif

39.endfor

40.endfor

41.untilstop=TRUE

42. findFk=argmaxFi∈FS{v{Fi}}

//寻找得到总利益最大的联盟进行虚拟机资源的分配

43. calculateψCi(Fk),Ci∈Fk

//计算所得联盟中云资源提供者的利益分割

44.Fkallocates and provides the requested VM instances

//完成VM实例的分配与提供

算法开始于用户发送的请求。联盟结构FS由单个Ci∈I构成一个联盟Fi的形式构成。然后，算法计算v(Fi)，利用矩阵visited记录FS中已被访问的合并过程中的所有联盟对。通过该矩阵，FS中所有可能的两个联盟组合在合并过程中均可被访问到。合并过程开始于随机选择FS中的两个未访问联盟，即Fi和Fj。调用B&B-VM-ALLOCATION可以找到在Fi∪Fj上的最优VM分配方案。如果Fi∪FjΔm{Fi,Fj}，则联盟Fi和Fj决定合并。Fi∪Fj被保存于Fi中，而Fj则从FS中移除。由于Fi发生改变，在下一轮合并步骤中该联盟依然可被选择。因此，对于所有的Fk∈FS，k≠i,visited[Fi][Fk]均设置为false。合并过程再次试图找到另一个未被访问适合于合并的联盟对。如果所有联盟均被测试，合并过程没有发生，大联盟得以形成，则合并过程终止。

通过合并过程得到的联盟结构FS接下来需要进行分裂过程。在分裂过程中，所有拥有一个以上成员的联盟均需要进行分裂测试。算法将拥有一个以上成员的联盟Fi分裂为两个不相交的联盟Fj和Fk，Fj∪Fk=Fi。B&B-VM-ALLOCATION被调用两次以找到在Fj和Fk上的最优分配方案。由于分裂过程是自私决策，只有当联盟Fj或Fk的成员之一可以改进其利益时才会发生联盟分裂行为，因此，拥有更高个体利益的联盟才是分裂行为的决策者。

如果一个或多个联盟分裂，则联盟合并过程重新开始，为此，stop标识符补充设置为false。连续多次的合并和分裂过程重复进行直到算法终止，终止即表明此时对于在FS中的所有已有联盟不会再选择进行联盟合并或分裂过程。考虑FSfinal作为算法得到的最终的联盟结构，算法将选择FSfinal中的一个可以得到最高总体利益的联盟作为任务调度的目标资源集合。算法利用标准化估计Banzhaf值计算联盟中参与的云资源提供者的个体利益，所选择的联盟将分配和提供给用户任务相应请求的VM实例。

2.3 算法性能分析

1) 算法收敛性能分析。根据联盟偏好关系Δm的定义可知，每一次迭代中，经过两个联盟合并后得到的联盟结构肯定优于联盟合并前的两个联盟。同理，根据联盟偏好关系Δs定义可知，经过单个联盟分裂后得到的联盟结构肯定优于分裂前的两个联盟结构。因此，如果经过联盟的合并与分裂迭代操作后得到了一个联盟结构，那么算法肯定无法在后续的联盟合并与分裂过程再次得到该联盟结构，即同样的联盟在合并与分裂过程中是不可逆的。同时，对于固定数量的云资源提供者而言，其能够得到的可能的联盟结构形式是有上限值的，联盟的合并和分裂迭代过程务必在一定的联盟数量上停止。综上所述，本文算法最终得到的联盟结构将是一个无法进一步合并与分裂的联盟结构，即算法肯定是收敛的。

2) 算法稳定性能分析。只要没有任意一个联盟中的云资源提供者在不降低至少一个其他联盟成员收益的情况下可以脱离联盟，则可以认为该联盟结构是具有稳定性的。在联盟分裂过程中，本文算法在当前联盟中的每个云资源提供者上遍历分裂出联盟的可能性。如果找到这一云资源提供者，则可以应用分裂规则。那么在最终的联盟结构中，没有一个云资源提供者会选择脱离联盟，即此时的联盟一定具有稳定性。云资源提供者组成的资源联盟一旦具有稳定性，就可以向用户方的任务提供请求的虚拟机实例。

3) 算法时间复杂度分析。理论上，求解使得联盟总体利益最大化的最优联盟结构问题与在所有云资源提供者上穷举出所有联盟分割结构问题具有同样的时间复杂度。然而，本文算法设计了联盟的合并与分裂机制，这样在寻优过程中是不需要列举出所有的联盟结构形式的，大大地降低了算法搜索的时间复杂度。同时，本文算法的时间复杂性主要由联盟进行的合并与分裂次数以及子联盟的规模(内部拥有的云资源提供者的数量)相关。首先，考虑搜索过程中的最坏情况。在联盟结构FS中，其每一个联盟均需要与其他所有联盟形式尝试合并。初始联盟结构中，单个云资源提供者均单独构成一个联盟，那么最坏的情形下，一共需要进行m(m-1)/2次尝试后，将进行第一次的联盟合并。而第二次合并则要求进行(m-1)(m-2)/2次合并的尝试，依此类推。则最坏的合并时间复杂度为O(m3)。此外，最坏情况下，联盟F分裂过程的时间复杂度为O(2|F|)，即需要将其分裂为所有可能形式的联盟对。因此，本文算法的实际时间复杂度应该远小于O(m3+2|F|)。

3 仿真实验

3.1 实验配置

在仿真平台CloudSim[15]中对算法进行性能验证。考虑由八个云资源提供者提供四种类型的VM实例的云资源提供环境，八个云资源提供者是实际环境中云资源间可以组建联盟的合理估算。四种VM实例类型VM={VM1,VM2,VM3,VM4}，分别代表small、medium、large、extra large的VM实例，VM实例的相关参数描述如表1所示。VM实例类型和定价机制与Microsoft Azure相似。

表1 可用的VM实例属性

3.2 结果分析

本文选取最优云联盟算法和随机云联盟算法作为对比算法。最优云联盟算法通过求解线性规划问题中式(7)所代表的松弛问题寻找最优的云资源提供者的分配方案。换言之，该算法寻找能够使其收益达到最大化的联盟结构，即通过穷举方法得到所有可能的联盟结构，并在这些联盟结构上求解所有的最优化问题的线性规划最优解。因此，该算法中并非所有云资源提供者都必须提供资源来完成请求。随机云联盟算法随机选择若干个云资源提供者组建一个联盟。以上三种算法均采用分支限界法求解最优化问题中的线性规划问题。考虑四种不同类型的用户请求为(10,0,0,0)、(10,10,0,0)、(10,10,10,0)、(10,10,10,10)，分别代表small、medium、large、extra large的VM请求。所有请求无法由单个云资源提供者完成，需要形成云资源提供者联盟才能满足用户需求。本实验执行了10次仿真，并以得到的平均值进行性能分析。

图1比较了本文算法与两个对比算法得到的总体利益情况，在所有测试场景中，本文算法均得到了与最优云联盟算法一样最高的利益。实验结果证明随机云联盟算法在联盟利益上并非是一种有效算法，例如：对于small型VM请求，本文算法和最优云联盟算法获得的总利益为＄6.81，而随机云联盟算法的总利益仅为＄4.8。

图1 云联盟的总体利益

图2是medium型VM请求时得到的联盟中每个参与云资源提供者的个体利益值的情况，比较了三种不同的利益分割方式。本文算法采用的是标准化估计Banzhaf值的利益分割方式，两种最优云联盟算法，一种利用标准化Banzhaf值进行利益分割，一种利用正比例利益方式进行利益在个体成员间的分配，而不使用Banzhaf值方式。这里，正比例利益分割方式意味着联盟中每个参与的云资源提供者得到了与其价格一样的利益分割，该价格为用户向资源支付的费用与云资源提供者的资源代价之差。本文算法和最优云联盟算法(标准化Banzhaf值)获得的总体利益为＄9.75，而两种算法找到的联盟规模为4，即{C2,C3,C4,C6}。本文算法搜索了53个联盟才找到最终的联盟结构，可以看出，本文算法与最优云联盟算法得到的联盟个体成员的利益分割是非常接近的。

图2 联盟中个体云资源提供者的利益

图3是三种算法的执行时间比较，该结果是从3.00 GHz Intel quad-core PC 4 GB内存的机器上运行得到的结果。对于8个云资源提供者可能形成的所有255个联盟中，本文算法根据提出的联盟合并和分裂规则仅仅考虑了其中部分联盟结构的测试。平均来说，本文算法需要搜索48个联盟才能找到最终的联盟结构。因此，本文算法的执行时间是远小于最优云联盟算法的，后者是一种穷举式方法，需要搜索所有的联盟形式。对于每个联盟，两种算法仅需要求解线性规划问题一次。对于large型VM请求，求解线性规划需要更多时间，两种算法的执行时间也将相应增加。随机云联盟算法的执行时间接近于0，因为它在单个联盟上执行一次线性规划求解过程的时间花费仅为3.3微秒。

图3 算法的执行时间

4 结 语

为了实现资源联盟的总体利益最大化，本文提出了一种云联盟形成博弈算法。利用高效的联盟合并与分裂机制，使云资源提供者能以稳定的联盟结构形态满足用户需求。此外，还设计了一种基于标准化估计Banshaf值法的总体利益在个体成员间的收益分割机制，不仅可以保证利益分配的公平性，而且还可以使得联盟成员不会产生脱离联盟结构的动机。