电偶极子与单摆

景雨薇，吴普训

(湖南师范大学 物理与电子科学学院，湖南 长沙 410081)

偶极子是电磁学基本模型之一[1-3]，是理解电介质极化的基础；在固体物理、天体物理、流体力学等广泛领域有重要应用[4,5].一般教材要么给出电势再做梯度计算，要么通过矢量叠加给出场强，推导比较数学化，学生难以对场强特点和物理图像获得直观理解.特别是所谓不依赖坐标的偶极子场强形式看起来颇为复杂，难以理解.那么，偶极子场强不同形式间有何联系？如何直观理解其物理图像？一般教材很少深入阐述.

本文用熟知的外场中偶极子势能公式，一步给出偶极子电势；然后，通过类比力学单摆给出偶极子场强的两种不同形式，清楚说明每个分量的物理意义，特别是所谓不依赖坐标的场强形式.最后，我们还讨论了该力电类比方法的特点，并给出应用实例.

1 偶极子电势：两种推导方法

如图1所示，偶极子由彼此靠近、间距为l的等量正负点电荷±q构成.以电荷连线中点为原点建立坐标系，场点P的电势[1]

图1 偶极子与单摆的类比示意图

(1)

(2)

现在我们给出一种更简捷的推导方法.按定义，V是单位电荷在偶极电场中的势能，即偶极子与单位电荷的相互作用能.既然是相互作用，式(2)也是偶极子在单位点电荷电场中的势能！外场中偶极子的势能是[2]

U=-p·E外

(3)

2 偶极子场强与单摆受力

对电势取梯度，即得场强

(4)

V=λz

(5)

对固定的r，竖直方向的电场是

(6)

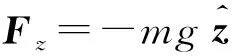
(E,V,λ)↔(F,U,mg)

(7)

可以把偶极子场强问题转化为熟知的单摆受力分析.注意，固定径向距离r时，λ可以视为常数，但是r的竖直投影z依然依赖角度变化.这跟摆长固定的单摆一样，即摆长的竖直投影z随摆的位置(摆角)而变化.上述映射仅在此特定情况下成立，即固定r的偶极子静电势能和固定摆长的单摆重力势能都跟z成线性关系.

既然势能形式相同，作为势函数梯度的力场形式自然也相同.例如，单摆切向力和径向力(向心力)分别是[3,6]：

Fα=mgsinα

(8)

(9)

(10)

(11)

与矢量叠加得到的熟知结果[2,3]完全一致.

从动力学角度分析，还可以更清楚看到上述映射的物理意义.考虑一个质量为m的单位正电荷从偶极子势能零点释放，初速度为零，那么该电荷运动是什么特点呢？根据力电类比，易猜测其运动类似单摆，即轨迹为半圆的周期运动，电荷往返于左右电势能零点[7]，中间势能最低点处速度最大(如图1).根据能量守恒定律，电势能差给出动能，从而推出向心力,该向心力恰对应偶极子径向场强，即

(12)

可见，映射式(8)不仅来自势能形式一致，而且来自动力学过程共同遵守的能量守恒定律,即静电或重力势能与动能相互转化.当然，无论电荷还是单摆，仅在势能最低点附近才遵从简谐振动，运动幅度增大时则为非线性运动[3].

3 偶极子场强：不依赖坐标的形式

利用力电类比方法，可以立即写出所谓不依赖坐标的偶极子电场强度，并且对各个分量能够获得直观的物理图像，因此初学者容易获得更深刻的印象.

(13)

这样很容易理解各分量的物理图像，特别是为什么第一项能写为向心分量，而第二项的方向始终固定不变.

这种不依赖坐标的场强形式特别有用，例如，结合式(3)和(13)即可以得到两个偶极子之间的相互作用能[8]

Udd=-p2·Ep=

(14)

这个结果用途很广，例如可以给出如水分子等极性分子之间的长程相互作用等[1,2].

4 讨论和总结

从计算角度看，教材中的传统方法，即要么给出电势然后取梯度运算，要么利用电场矢量叠加，不一定比力电类比方法更难.但是相比纯数学计算，力电类比法有独特的优点：首先，把力学和电磁学两个最基本的模型联系起来，对从不同角度体会知识点的联系颇有价值；其次，力电类比可立即给出不依赖坐标形式的电场，清楚看到各分量的物理图像(类比重力和拉力)；最后，该方法对解决某些问题特别简捷，例如计算从偶极势能最低点附近释放的电荷谐振动频率或周期，就可以用单摆熟知结果立即给出[3，9].当然，单摆和偶极子映射关系背后是否隐藏着更丰富的物理和更奇妙的应用，值得我们未来开展更多深入研究.

从更广阔视角看，利用数学方程相似性，把看似相距遥远的两个不同物理系统联系起来，这样的类比思想在物理中不乏其例：LC电路与谐振子[2]，偶极电场与球附近流体速度场[10],全反射光透射与物质波遂穿[11]，等.正如物理学家费曼说：“物理学有一个最引人注目的吻合，即多种不同情况的方程有完全相同的形式.这意味着学习了一个学科，我们立即拥有大量精确的关于另一门学科的知识.”[2]