基于太阳风暴的月球内部结构探测方法研究

王广君 宋梦兰 张艺腾 徐彩凤

（1. 中国地质大学（武汉）自动化学院，武汉 430074；2. 复杂系统先进控制与智能自动化湖北省重点实验室，武汉 430074；3. 中国科学院国家空间科学中心 空间天气学国家重点实验室，北京 100190；4. 中科-莘县联合研发中心，聊城 252400）

引 言

月球是地球唯一的天然卫星，与太阳系的其他自然天体相比，月球离地球最近，是人类进行太空探索的首选目标. 月球探测是人类探索太空的第一步，有助于提高人类对月球、地月空间的认知，推动航天工程技术体系的进步与发展，为后续探索其他行星奠定坚实基础.

为了加深对月球的了解，人类利用各种方法对月球进行探测. 月球内部结构探测技术的发展可分为以下三个阶段：第一阶段是早期卫星观测，实现了对月球的初步认知，发现了月球上高密度异常体即质量瘤的存在[1]；第二阶段加入月震数据，通过月面观测-月震数据获取手段，得出月球圈层结构轮廓，大致可划分为月壳、月幔、月核[2-3]；随着1994年美国Clementine探测器的成功发射，月球内部结构的研究进入第三阶段，即月球高分辨率遥感观测与月震数据的综合应用阶段，深化了对月球内部结构的认识[4-5]. 常用的月球内部结构探测方法主要有基于物理场分布特征如月球重力场[6-7]、磁场[8]、月震波[9-10]等，基于激光测距[11]以及基于微波遥感技术的月球结构探测方法. 微波遥感技术主要用于浅层月壳结构探测，而月球重力场常用于研究上月幔-月壳内部结构，还可用于推断月壳厚度. 月震观测法是最有效、最直接获取月球内部结构的重要手段，目前使用的月震数据主要来源于Apollo号登月时布置的月震观测网[12].其他研究方法或多或少将月震获取的内部结构作为先验知识. 但是，自1972年Apollo计划终止至今，没有新的月震仪投放到月球，使得目前可用的月震数据依旧是Apollo时期的12000余条[13]. 况且，运用不同月震数据反演月球结构时，得出的结果不完全相同，甚至自相矛盾.

近年来，随着科技的发展，大量月球探测器发射，使得人们可以获取更多更高质量的月球探测数据，为进一步研究月球内部结构提供了条件. 瞬变电磁法（transient electromagnetic methods，TEM）[14]是地球物理勘探中的一种重要的电磁探测方法，在资源开采、地质灾害防治等方面取得了较为理想的探测结果[15]. 但是TEM仅仅能够探测地下数千米的地质结构，探测范围较小，且其探测装置复杂，探测过程较为繁琐，无法直接应用于月球内部结构探测. 针对这些问题，本文借助太阳风暴，结合TEM探测方法，提出了一种基于太阳风暴的月球内部结构探测方法，为月球内部结构探测提供新思路.

1 太阳风暴对月球磁场的影响

太阳风暴是指太阳黑子引起的耀斑剧烈爆发活动，是一种持续时间短暂、规模巨大的能量释放现象，主要以电磁辐射、高能带电粒子流和等离子体云等三种形式释放，这些物质在行星际空间传播，并且和行星际介质、磁场相互作用，进而影响到整个太阳系的空间环境[16]. 太阳风暴喷射的物质和能量到达月球空间后，不但会导致月球表面受到侵蚀，也会损害月球的大气.

月球不具备全球性偶极磁场，无法形成大尺度磁层结构. 当太阳风暴袭击月球时，会在极短的时间内对月球磁场产生显著影响，发生磁场跃变现象. 跃变的脉冲磁场向月球地表下方扩散，使月球的地质体发生极化，在月球内部激发感应涡流，如图1所示. 当磁场跃变停止，月球磁场处于相对稳定的状态时，月球内部激发的感应涡电流会产生感应磁场并向月球表面辐射. 感应涡流的扩散速度快慢取决于介质的电导率高低，在低电导率的介质中，感应涡流的扩散速度快；在高电导率的介质中，感应涡流的扩散速度慢. 因此，感应磁场信号的衰减过程会随着月球内部地质结构的改变而发生变化.

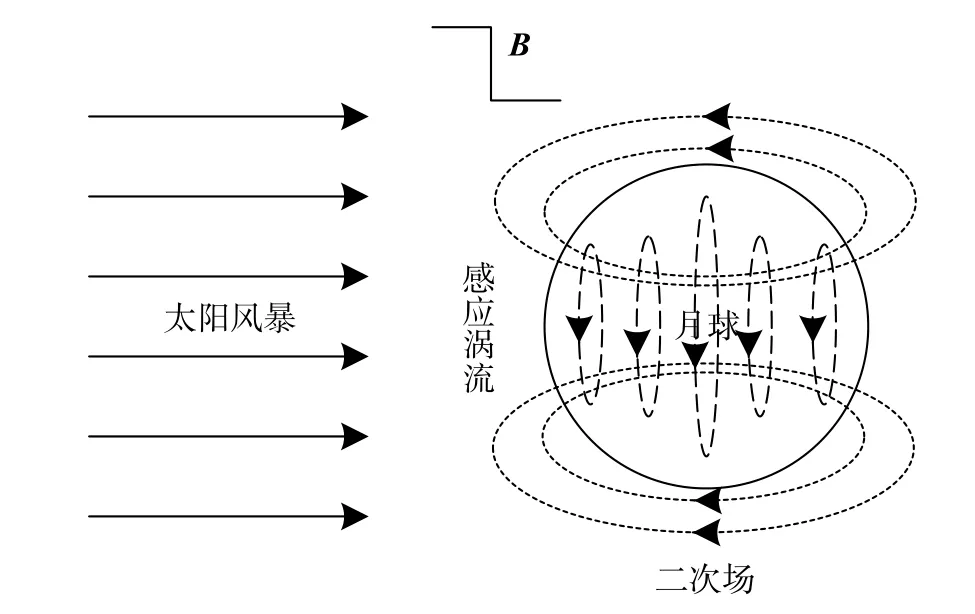
图1 基于太阳风暴的月球内部结构探测示意图Fig. 1 Schematic diagram of lunar interior structure detection based on solar storm

感应磁场信号的时间和空间特征能够反映月球内部地质结构的电性分布状态，可用于判断月球内部地质结构. 在实际探测过程中，在月球表面利用高精度的磁传感器测量磁场信号的磁感应强度，所测信号为月球外源磁场与感应磁场信号的叠加信号，不能直接用于后续的计算处理. 为了提取纯净的感应磁场信号，要先测量被测位置的外源磁场信号，再对原始测量数据进行处理. 最后通过对纯净的感应磁场信号进行计算，获取其中蕴含的电性信息，从而判断月球内部结构.

2 基于太阳风暴的月球内部结构探测

TEM是利用不接地回线向下发射由阶跃波形电磁脉冲激发的一次场，在一次脉冲电磁场的间歇期间（断电），会产生一个二次场的感应涡流场.感应涡流场会以一定的规律随时间变化，包含着与地质体有关的信息. 在实际观测中，常通过接收线圈观测一次场脉冲间歇期间随时间衰减变化的二次场信号，从而通过反演解释得出地下地质信息.

在月球内部结构探测中，TEM探测方法存在下列问题：一是探测深度小；二是脉冲磁场的生成方式. TEM的探测深度可由下式表示[17]：

式中：M为发射磁矩，M=IS，其中I为发射电流，S为发射线圈面积；ρ为电阻率，单位为 Ω·m ；η为最小可分辨电压. 由式(1)可知，TEM的探测深度与发射电流磁矩及地质体的电阻率有关.

目前地球物理应用中，TEM的探测深度最深可达地下几千米，但是月球的平均半径为1738 km，两者相差极大，TEM无法满足月球内部探测的深度要求. 在进行地质探测时，TEM发射机利用不接地回线或接地线源向地下发射脉冲磁场极化地下地质体[18]，属于人工源探测. 由式(1)可知，发射磁矩会影响探测深度，可通过增强发射磁矩来增大TEM探测深度. 但是发射磁矩的增加对TEM发射机的功率提出了更高的要求，而现有的TEM仪器无法满足月球探测所需的功率要求，无法生成足够强的脉冲磁场.

基于太阳风暴的月球内部结构探测方法，利用太阳风暴引起的月球磁场跃变作为激励源使地下地质体极化产生感应磁场，通过对感应磁场进行计算和分析以达到了解月球内部结构的目的.太阳风暴作用下的磁场跃变产生的磁矩远大于人工源产生的磁矩，故利用太阳风暴可大大提高探测深度. 假设月球是由不同介质的层状结构组成，在太阳风磁场作用下，不同层状介质会产生极化.太阳风暴消失后，这些极化的介质会产生二次场电磁信息. 二次场电磁信号的传播符合麦克斯韦方程组，由麦克斯韦方程组推导的二次场传播过程，就是TEM正演. TEM探测中，正演是反演得到地质体结构的基础.

由于太阳风暴作用下的磁场跃变持续时间极短，可将其视为瞬变磁场. 太阳风暴产生的磁场可等效于一个圆形线圈产生的磁场，将一个载有电流的圆形回路作为磁偶极子的模型，如图2所示.

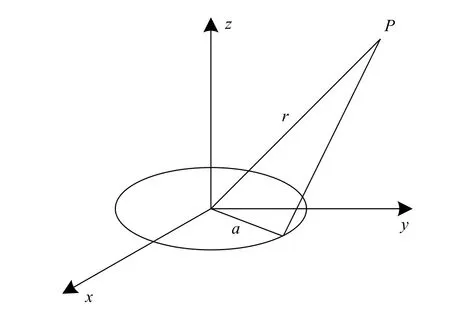
图2 磁偶极子示意图Fig. 2 Schematic diagram of the magnetic dipole

磁偶极子场中一点P的磁场场强表达式为

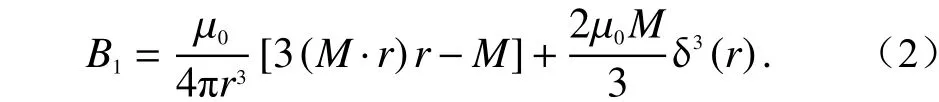
式中：r为真空磁偶极子到空间一点的距离；磁偶极子磁矩M=IS，其中I为等效回路电流，S为发射线圈面积，S=πa2(a为 等效发射线圈半径)； µ0为真空磁导率； δ(r)为狄拉克函数.

当r≠0时，δ(r)=0，由式(2)有

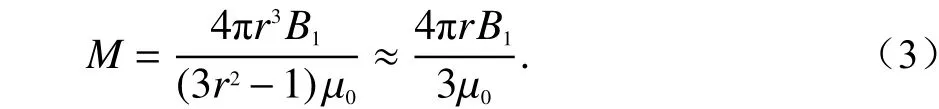
式中，B1为太阳风暴作用下的磁场跃变量. 则可得等效回路电流如下：

以阶跃电流为激励源时，水平层状大地中心回线装置垂直方向的频率域响应为[19]

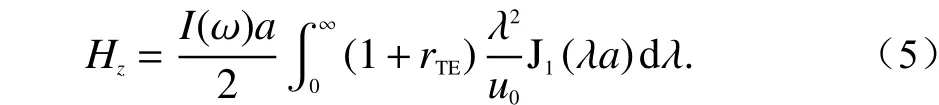
式中：rTE为反射系数；为真空中的传播波数；J1为一阶贝塞尔函数；其中kx、ky为x、y方向上的空间波数. 将式(4)等效电流代入式(5)可得，以磁场跃变为激励源时，月球垂直方向的频率域响应为

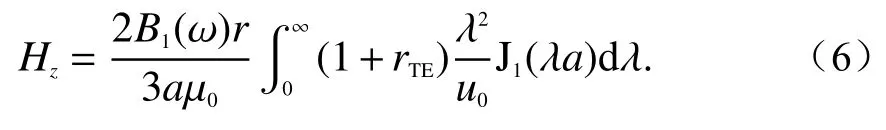
由于r≥a，假设月球到太阳风暴作用下磁场的等效发射线圈的距离r取值为线圈半径的10倍，即r=10a，则式(6)可转化为

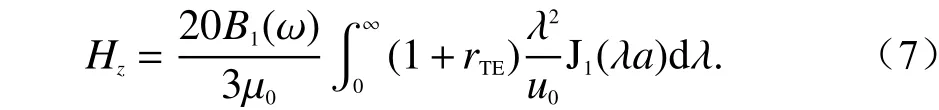
由于太阳风暴作用下的月球磁场跃变，假设跃变磁场表达式如下：

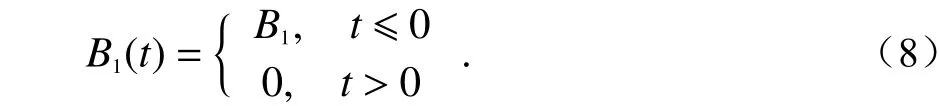
则有

磁场强度是由磁感应强度与磁导率定义而来，在真空中，两者的关系为

将式(8)代入式(6)并用s替代 iω后，代入式(9)有域的转换，将s=j·ln2/t代入式(10)可得

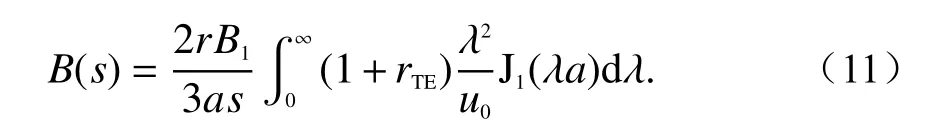
实际获得的信号为时间域信号，因此应将频率域信号转换为时间域信号. 频-时域转换方法主要有：傅里叶变换法、延迟谱方法、G-S逆拉氏变换方法、数字滤波方法[20]等. 相比于其他方法，GS变换法是纯实数计算，计算过程简单明了，性能较为优越. 故本文利用G-S变换实现频率域到时间本文综合考虑误差与适用区间，选取n=10；Kj为G-S变换系数，其计算方法为

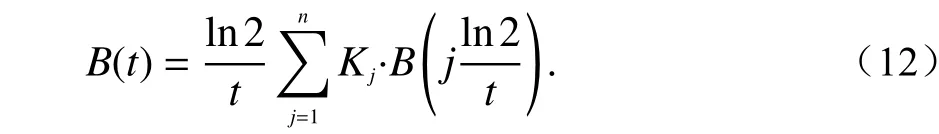
式中：t为取样时间；n的取值目前没有统一意见，

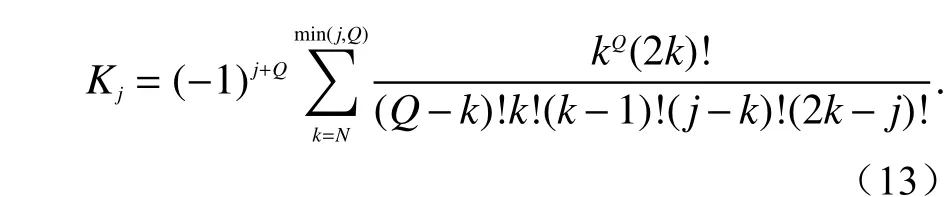
式中：Q=n/2；N=(j+1)/2 .

式(12)含有一阶贝塞尔无限积分，利用汉克尔变换求解一阶贝塞尔函数，可得出时间域月球磁感应强度：

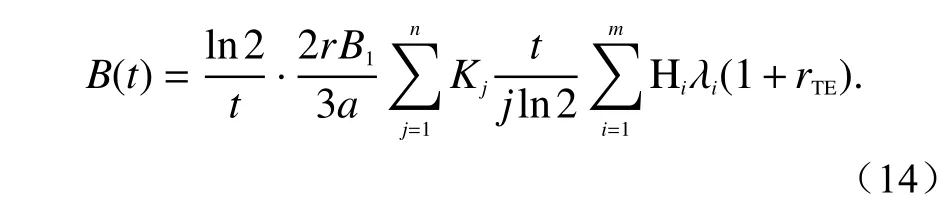
式中： Hi为汉克尔滤波系数；本文采用140点滤波 系 数，则m=140； λi为 抽 样 点，其 取 值 为10[b+(i−1)c].

3 仿真实验验证

经过卫星探测可知，月球本身是一个不均匀的球体，为了简化计算，本文将月球视为一个均匀的球体，并忽略月球本身极其微弱的磁场，以此为基础，结合现有的资料，设定了三种月球的地质模型：月球均匀不分层模型、月球均匀双层模型、月球均匀三层模型.

3.1 月球均匀不分层模型正演结果

不考虑月球电阻率的横向梯度和不同区域地形高差变化，假设月球是一个各向同性的不分层均匀介质球体，具有单一电阻率，即月球地质模型为均匀不分层模型，其模型结构如图3所示.

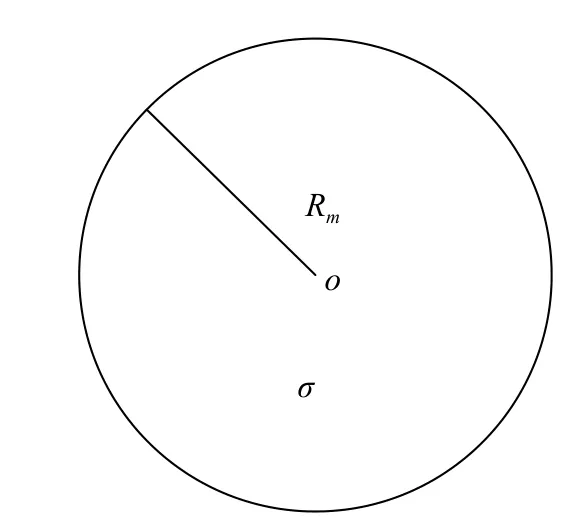
图3 均匀不分层月球模型Fig. 3 Evenly non-stratified lunar model

基于太阳风暴的月球内部结构探测方法的基石是不同电阻率对应的电磁响应信号也不同，要想验证月球内部结构探测方法的有效性，必须了解电阻率对响应信号的影响. 设定月球磁场在t=0 时刻发生了变化量为 50nT的磁场跃变，月球电阻率分别为105Ω·m、106Ω·m、107Ω·m，月球的平均半径R=1738 km，对其取对数等间隔作正演模拟，其正演模拟的结果即磁感应强度曲线如图4所示.

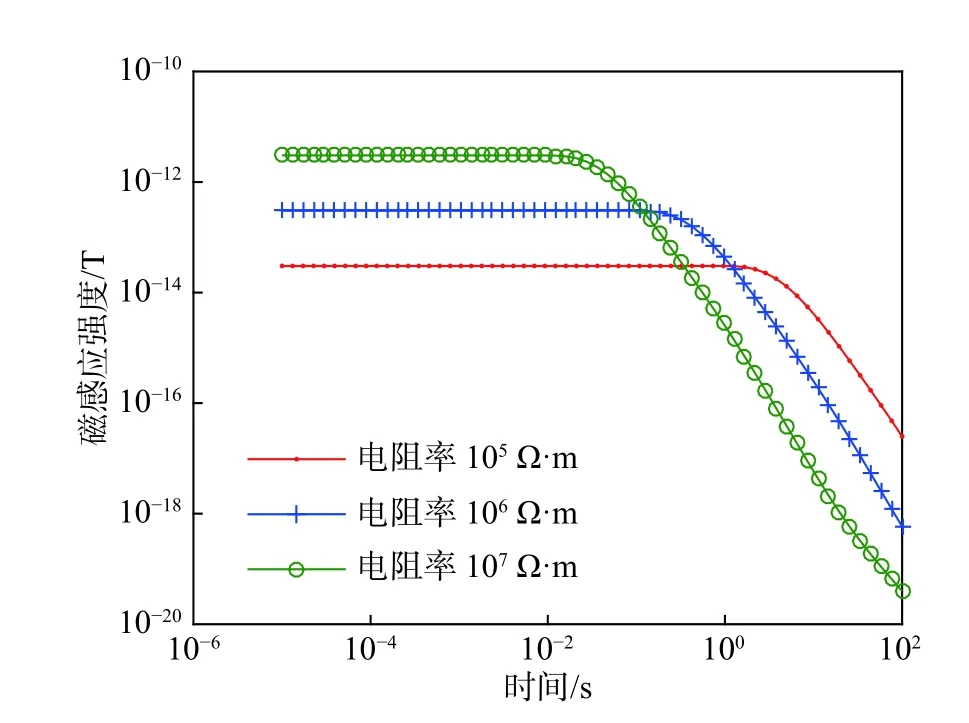
图4 均匀不分层模型下不同电阻率时的电磁响应曲线Fig. 4 Electromagnetic response curves of evenly nonstratified model at different resistivities

从图4可看出，在双对数坐标系下，电磁响应的早期曲线几乎平行于时间轴，而晚期曲线接近一条斜率为负数的直线. 说明早期接收到的电磁响应信号较强，然后随着时间开始衰减. 当月球电阻率取值不同时，瞬变响应曲线走向大体一致. 早期时，响应曲线几乎平行，由于瞬变响应在高阻中衰减比在低阻中快，所以电阻率较高的地层，电磁响应信号越早进入晚期.

通过以上分析可知，对于不同的电阻率，电磁响应信号的强度和衰减趋势存在差异，说明不同电阻率对应的电磁响应信号存在差异，可根据电磁响应信号的特征判断介质电阻率.

3.2 月球均匀双层模型正演结果

地质结构不同，介质电阻率也不同. 为了解不同地质结构电磁响应信号的变化趋势，假设月球内部由两层均匀介质组成，且两层介质的电阻率不同，对感应磁场进行模拟计算. 设定月球磁场在t=0 时刻有 50nT 的磁场跃变，其结构参数如图5所示，月球的平均半径R=1738 km.

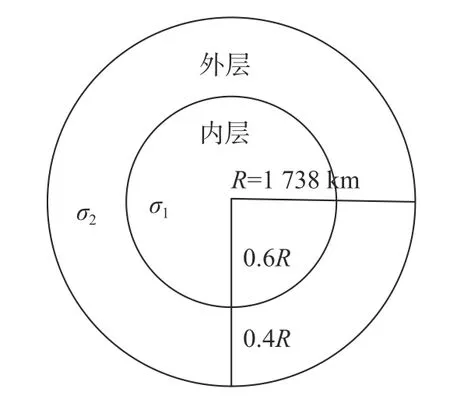
图5 均匀双层月球模型Fig. 5 Uniform double-layered lunar model

设定仿真模型参数如表1所示，正演模拟的结果即磁感应强度曲线如图6所示.

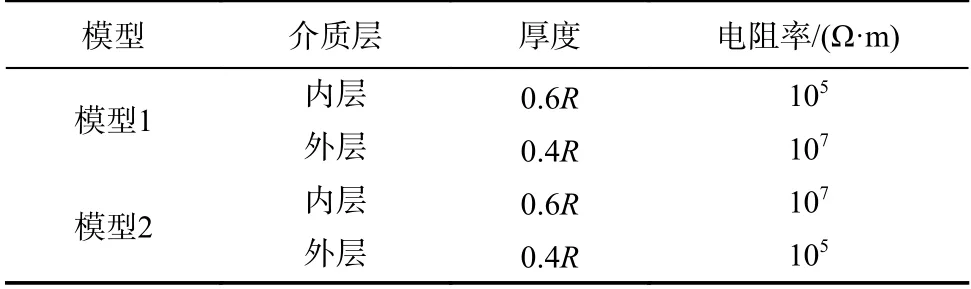
表1 均匀双层月球模型参数Tab. 1 Uniform double-layered model parameters

如图6所示，响应信号早期占主导地位的是月球外层，信号中期的响应信号是月球内层和月球外层共同作用的结果，在响应信号后期占主导地位的是月球内层.

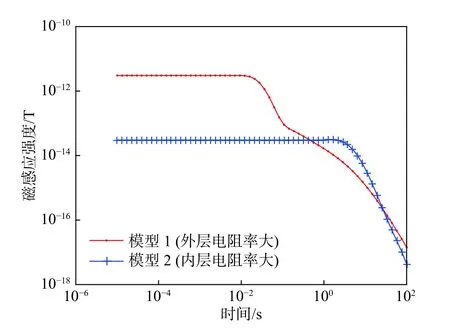
图6 均匀双层模型下不同地质结构的电磁响应曲线Fig. 6 Electromagnetic response curves of geological structures of uniform double-layered model

对于第1种月球模型，外层电阻率较大，所以早期信号强且衰减速度快；中期响应信号是由外层晚期信号和内层早期信号叠加而成，其下降趋势减缓；到了信号后期，内层晚期信号占主导地位，其下降趋势又开始加剧，且因为内层电阻率小，磁场衰减速度慢，下降趋势比早期下降趋势要平缓. 对于第2种月球模型，最开始的响应信号以月球外层信号为主，外层电阻率较小，电磁信号扩散速度慢，所以早期信号相对较弱且长时间都没有出现明显的衰减现象；中期响应信号是由外层晚期信号和内层早期信号叠加而成，由于内层信号早期信号强，而外层晚期信号较弱，所以出现上升现象，随着时间的延长，内层信号开始衰减，使叠加信号开始减弱；直至信号后期，内层晚期信号占主导地位，信号开始急剧衰减.

从上述分析可知，地质结构不同时，电磁响应信号特征的变化趋势也大不相同，说明电磁响应信号可以反映月球内部结构的电阻率变化，验证了探测方法的可行性. 电磁响应信号的变化趋势与理论分析相同，证明了正演算法的正确性.

3.3 月球均匀三层模型正演结果

从现有的研究看，研究者们更倾向于将月球从外到内分为月壳、月幔、月核三层结构，且三层介质电阻率各不相同. 现有的研究关于月球内部各层厚度及各层电阻率说法不一. 文献[13]给出的月球内部三层结构较被认可，其模型中月核、月幔、月壳的厚度分别为0.29R、0.67R及0.04R. 故现假设月球均匀三层结构如图7所示.

现有的研究表明月核、月壳电导率分别为10−2S/m 、1 0−9S/m，由于月幔厚度大且结构复杂，所以关于月球月幔电导率说法不一，但是均在10−7～10−5S/m[21]. 根据调研结果，本文假定月核电阻率为1 02Ω·m，月壳电阻率为1 09Ω·m，月幔电阻率分别为 105Ω·m、 106Ω·m及 107Ω·m的三种仿真模型，模型参数如表2所示. 设定月球磁场在t=0 时刻有 50nT的磁场跃变，分别对其进行正演计算，其正演模拟的结果即磁感应强度曲线如图8所示.

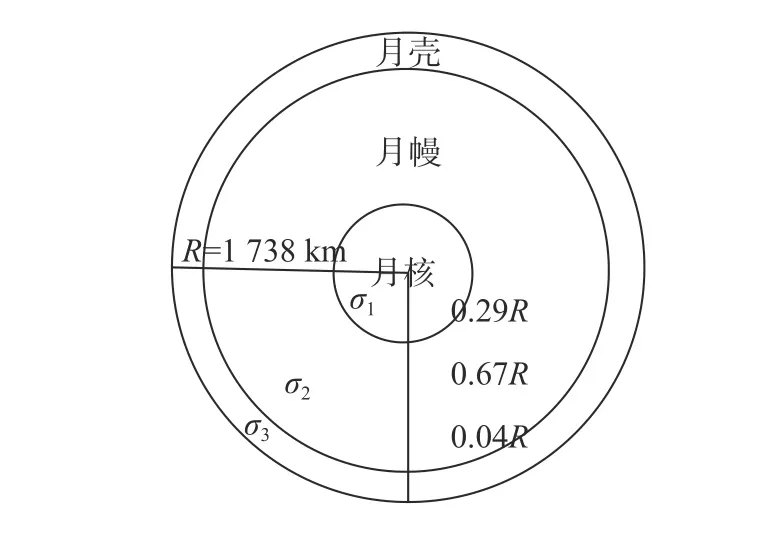
图7 均匀三层月球模型Fig. 7 Uniform three-layered lunar model

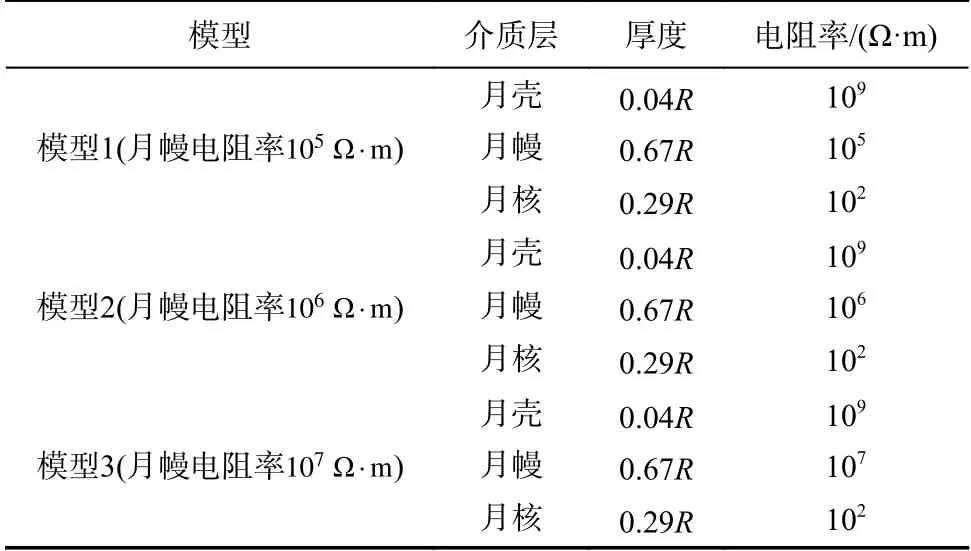
表2 均匀三层月球模型参数Tab. 2 Uniform three-layered model parameters

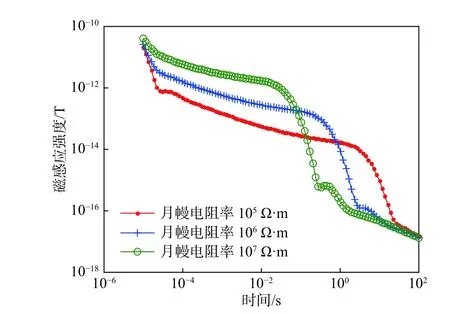
图8 均匀三层模型下不同月幔电阻率的电磁响应曲线Fig. 8 Electromagnetic response curves of uniform threelayered model at different lunar mantle resistivities

图8中三种模型的区别主要是月幔的电阻率不同，其月壳的电阻率相同，但月壳厚度较小，故月壳电阻率只在开始的极短时间内对电磁信号产生较大的影响，而后月幔电阻率占据主导地位；月核的电阻率相同，所以其响应曲线趋近于一致.

月壳电阻率大导致早期信号快速衰减，同时由于月幔电阻率比月壳电阻率小，则在月幔电阻率的影响下，早期信号的衰减稍稍减缓. 当月幔电阻率为1 05Ω·m时 ，从月壳电阻率的1 09Ω·m到月幔电阻率的1 05Ω·m变化太大，使得早期信号出现明显的突变. 但由于月幔厚度大，所以在接下来的相当长一段时间内月幔电阻率对电磁信号的影响占据主导地位. 月幔电阻率越大，电磁信号衰减越快，符合均匀不分层模型的电磁响应结果. 与均匀不分层模型结果图4相比，三层模型前期信号有明显的下降趋势，主要是月壳电阻率与月幔电阻率综合作用的结果，较大的月壳电阻率使得前期数据衰减加速；同时晚期信号下降较为缓慢，主要是月幔电阻率与月核电阻率综合作用的结果，月核较小的电阻率使得晚期数据衰减趋势减缓. 当月幔电阻率为1 06Ω·m 及 1 07Ω·m时，晚期数据出现明显突变，同样是由于月幔电阻率较大，与月核电阻率的1 02Ω·m相差太大，从而造成电磁信号突变.

从上述分析可知，对于月球均匀三层模型，不同月幔电阻率主要影响电磁响应中期信号，仿真结果与理论分析一致，可见利用TEM可有效分辨月球内部电阻率的变化，进一步验证了基于太阳风暴的月球内部结构探测方法的可行性.

3.4 月幔细分模型正演结果

从以上三种模型正演结果可知，磁感应强度较小，不同月球模型下瞬变电磁信号强度均在10−17～10−10T，晚期信号极其微弱. 而资料显示，现有的磁强计只能实现1 0−15T以上磁场强度的测量.所以，从3.3节三种模型的正演结果看，现有条件的限制使得基于太阳风暴的TEM无法实现月球深部的探测，故将月幔部分细分再进行正演仿真，结合实际条件验证本文算法的可行性.

基于3.3节的月球均匀三层模型中的模型2，结合现有的资料，将其中月幔部分细分为两层（上月幔、下月幔），深度740 km处是上月幔和下月幔的分界面[13]. 再进一步将月幔划分为三层（上月幔、中月幔、下月幔）进行仿真实验，其结构及模型参数如表3所示，仿真结果如图9所示.

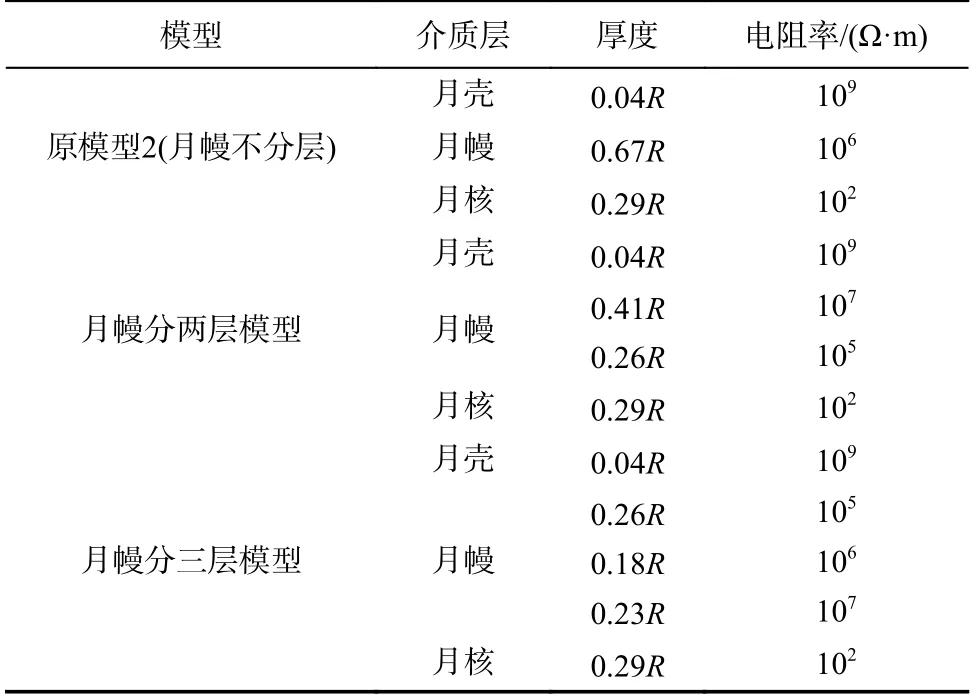
表3 月幔细分模型参数Tab. 3 Subdivided lunar mantle model parameters

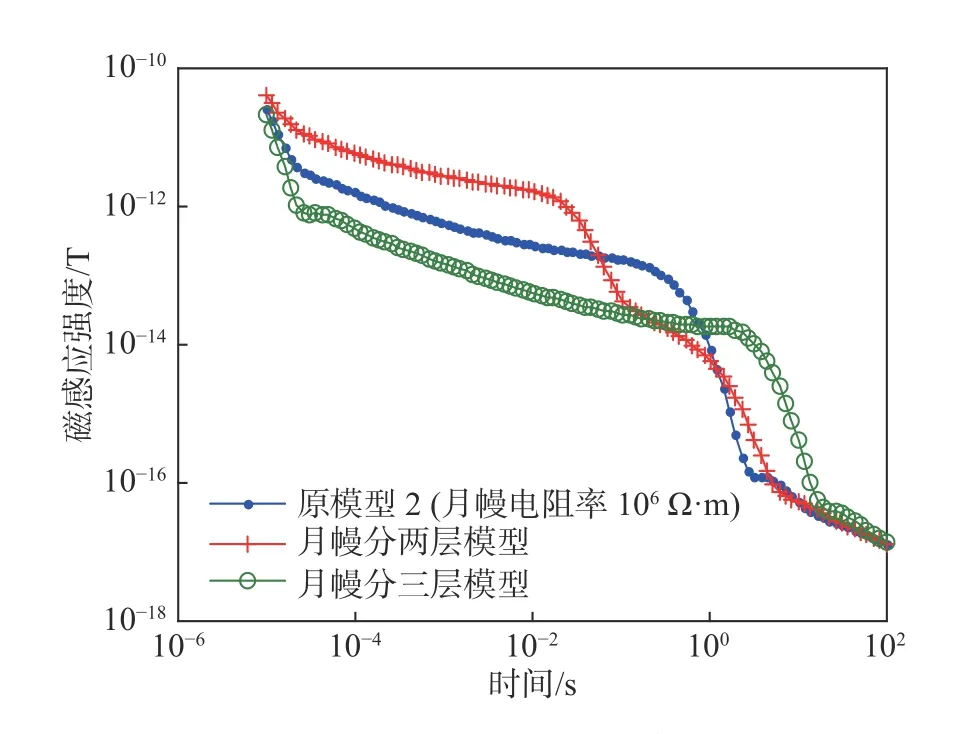
图9 月幔细分模型电磁响应曲线Fig. 9 Electromagnetic response curves of subdivided lunar mantle model

从仿真结果可以看出，月幔结构细分后，电磁响应曲线总体趋势一致，在磁强计的测量范围内能有效反映月幔结构的变化. 可见即使受到现有磁强计精度的限制，基于太阳风暴的TEM也能有效探测到月球内部月壳及月幔部分的地质结构，结合实际情况进一步验证了本文提出的月球内部结构探测方法的有效性.

4 结 论

本文提出了一种基于太阳风暴的月球内部结构探测方法. 该方法利用太阳风暴产生的磁场跃变作为探测源，使月球内部产生极化，当磁场跃变停止时，月球内部会向月球表面发射感应磁场信号，通过对感应磁场信号进行接收和处理便可获得月球内部结构信息. 本文分别对不同电阻率和不同地质结构的月球模型进行正演仿真试验，得到电磁响应曲线并作出细致的分析，证明其仿真结果特性与理论分析相符合，验证了月球探测方法的合理性与可靠性.

实际的月球探测更为复杂，本文提出的月球探测方法忽略了下列问题：1)探测位置对响应信号的影响. 月球不同纬度地区的地貌存在较大区别，太阳风暴对不同地区的磁场造成的影响也存在差异，因此，不同探测位置的二次感应磁场的幅、频变化趋势不同，在实际探测过程中，应考虑探测位置对响应信号的影响. 2)太空中的电磁干扰. 电磁干扰主要是指来自银河星系和太阳的电磁辐射所造成的干扰，会使探测信号中混杂大量噪声，不利于后续的信号处理.

月球内部结构较为复杂，探测难度极高，本文提出了基于太阳风暴的月球内部结构探测方法，并通过正演算法验证了不同的地质结构所得到的探测信号也会不同，验证了该方法的有效性，为月球内部结构探测方法提供了新思路.