一种基于工件偏转的激光线扫描误差补偿方法*
2021-03-15张仁伟孙晨晋孙明浩周志龙于斌超
张仁伟,孙晨晋,孙明浩,武 琼,周志龙,于斌超,刘 巍
(大连理工大学 机械工程学院,辽宁 大连 116023)
随着大型装备制造的快速发展,加工目标呈大尺寸、结构复杂等趋势,且局部小范围区域内精度要求高,因此,为保证局部区域的加工精度,必须实现局部小范围的面形高精扫描[1-3]。线激光扫描技术具有精度高、方便快捷、测量速度快等优点,在获取零部件形位信息方面得到了广泛应用[4-6]。
激光线扫描仪可直接将零部件点云数据传输到上位机,快速获取所需的几何特征。激光线扫描仪在采集复杂零件结构时,存在仪器误差、结构本身误差、安装误差和测量误差等,导致测量精度低。因此,研究面向激光线扫描技术的误差补偿方法,理论与工程价值明显[7-8]。安慰宁等[9]利用飞秒光频梳频域干涉的绝对测距方法,实现了激光线扫描仪的误差校正和输出控制。张亚等[10]分析了激光扫描技术在三维重建中存在的仪器扫描误差、数据拼接误差等因素,为激光扫描技术点云数据的处理和精度提高提供了重要参考。姚春荣等[11-12]通过线激光扫描方式,针对不同扫描速度下所采集的点云数据,提出了一种通过最小二乘法分区间建立误差预测模型以实现误差修正的新方法。邾继贵等[13]提出了基于激光线扫描传感器和通用工业机器人的测量方法,实现了自由曲面物体形貌的高精高效获取。郝春艳等[14]获得了扫描补偿系统中的多源误差及其相互影响关系,构建了误差分析模型。
与上述研究不同,为了提高激光线扫描仪的测量精度,提出了一种基于工件偏转角的光学误差补偿方法,以工件偏转点为突破点,结合设备安装位姿及待测目标结构特点,首先制定了目标点云数据的提取方案,然后构建了工件偏转及安装误差的补偿方法,有效提高了系统测量精度。
1 局部激光线扫描三角测量方法
局部激光线扫描三角测量方法属于点式或线定向,物体表面上点的绝对距离由参考平面确定。该方法所获得的距离为一维数据,测量过程中,首先将激光投射到待测目标物表面,然后利用反光信息和运动特征,获得运动轮廓的二维坐标[15-17]。局部激光线扫描三角测量原理如图1所示,采用激光二极管投射激光,感光片等敏感元器件接收发射光,最终实现光学信号的自输出与解码。

图1 局部激光线扫描三角测量原理
激光入射光通过二极管发射,经过透镜组的折射之后,聚焦到被测目标物体表面,发射回来的光通过滤镜透镜组,投射至线性半导体感光片阵列上实现数据传输。待测距离各异,光路结构不同,因此反射光斑质心位置亦存在差异,入射点到被测目标物体表面的几何参数可利用信号处理器的内部几何运算求得。
2 目标数据预处理
被测件表面主要为曲率半径较小的曲面和具有一定倾斜角度的斜面,采用激光线扫描仪局部测量系统可以实现对被测目标的快速扫掠,进而获取其空间三维点云数据,然而,由于存在外界环境光干扰,导致相关点云数据存在粗差,如果将此类粗差数据直接用于后处理的补偿和转换计算,必然会严重影响数据精度。因此,基于Ransac算法,利用非线性误差消除技术,实现点云数据的预处理。
提出了一种采用基于曲面特征的Ransac优化模型,其原理如图2所示。通过测量获取的所有点云数据的集合记为N。首先,将点云集合N降为二维数据,然后获得该分辨率下的曲线,记为集合n;逐个选取集合n中的曲线ni,然后抽取4组数据点,求解4组数据点的多项式矩阵k。进一步,对ni中包含的数据点进行{nii↔Nii} 精度测试,若符合条件‖knii-Nii‖
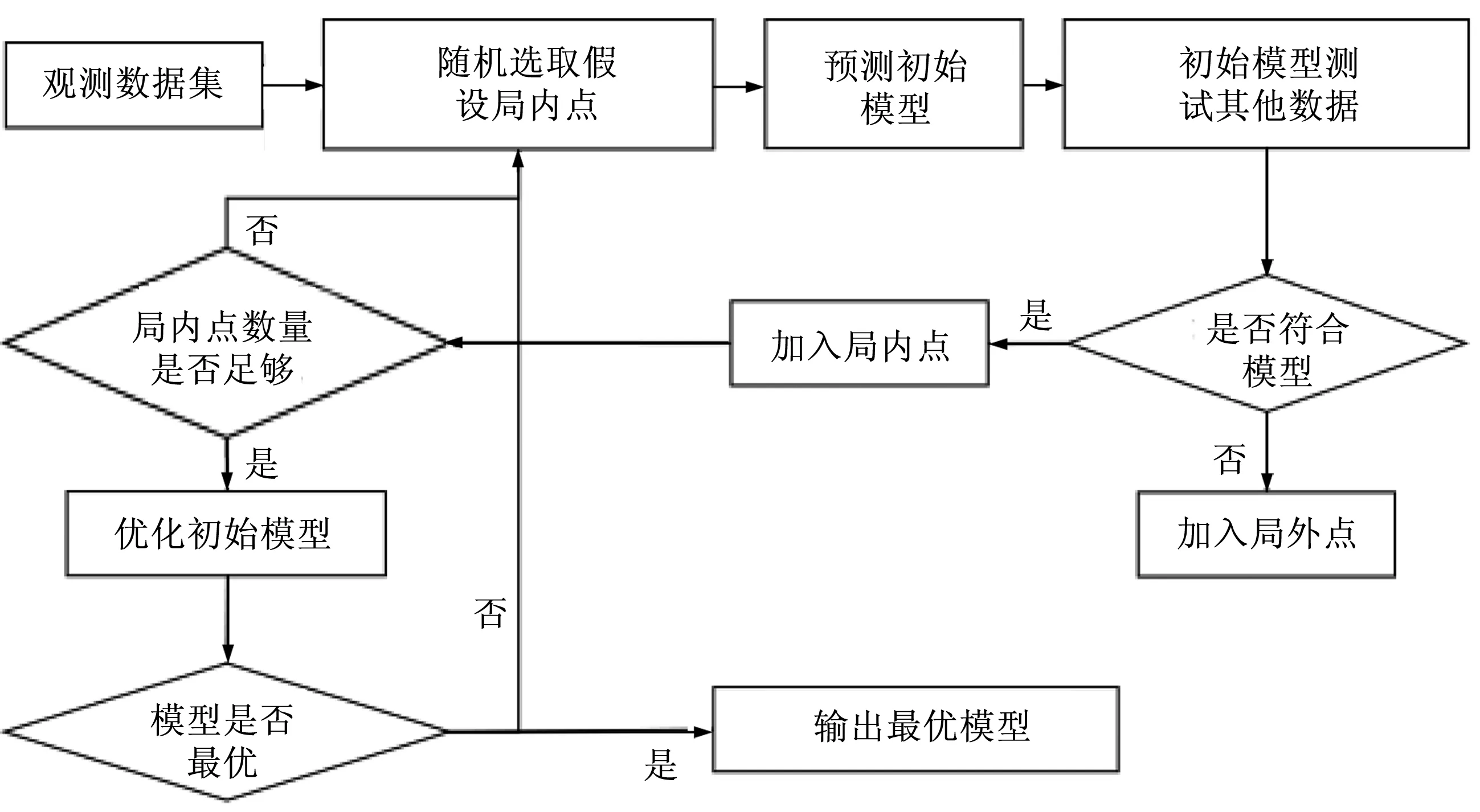
图2 采用Ransac算法的参数获取模型
3 基于工件偏转的误差补偿方法
激光线扫描仪产生的入射光垂直投射到待测目标物体后,在被测工件表面必将产生调制效应,由于漫反射而产生空间散射场。透镜聚焦的反射光线被内部屏幕接收,获得成像光斑,进而输出物体表面距离的数据信息,其变化由光能质心位置所决定。激光线扫描三角测量方法的理论前提是入射激光成像点近似为精确点,实际测量曲面和倾斜面特征时,入射光与物体表面之间的夹角难以达到90°,光斑直径较大,必然引入系统误差,精度下降。
3.1 基于工件偏转的光能分布
被测工件表面存在一定的曲率和倾斜,测量表面的偏转导致结果失准,在工件偏转时三角测量方法需调整。假设工件实时偏转角为γ,工件偏转时的测量原理图如图3所示。
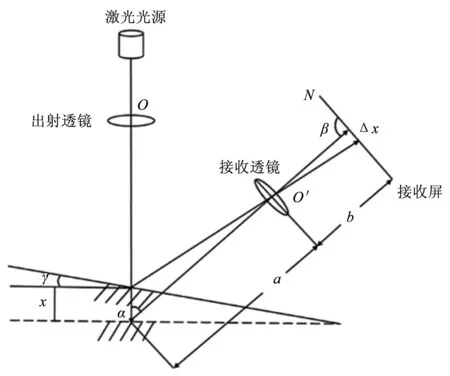
图3 工件偏转时的测量原理图
在图3中,入射光穿过出射透镜O,在工件表面发生反射,反射光穿过接收透镜O′聚焦于反射光接收屏上,x为工件的深度,Δx为对应变化量。在工件倾斜时,准确求解光能质心位置,减少激光线扫描仪测量误差。在测量阶段,建立强针对性的非线性回归模型,进行三角测量光学评估,同时根据灵敏度分析参数变量。
漫反射时,在空间立体角度中,入射光线的辐射能量的分布满足余弦变化关系
I(θ)=I0cosθ
(1)
式中,θ为目标面法向与反射光线的夹角;I(θ)是反射光功率;I0为表面法向矢量方向下的角散射光功率。
设激光线扫描仪接收半径为R,空间反射光场近似呈均匀分布,接收透镜的光场能量E为:
(2)
式中,σ为入射立体角;a为原始被测工件特征点至接收透镜中心的距离;ra为工件表面光点与接收透镜光心的距离;α为入射、反射光线的夹角;β为反射光线与接收屏的夹角。
进一步获得接收透镜的光场能量为
(3)
实现光能质心的定位可减少激光线扫描仪的光学测量误差。接下来,结合光场能量分布求解位移误差,建立基于工件偏转的误差补偿模型。
3.2 基于工件偏转的误差补偿方法
基于光学几何原理,对入射光进行能量积分,当光能中心线处两侧光能量积分相等时,关系表达式为
(4)
式中,x′为光能中心线在接收屏上的投射坐标;φ为接收透镜光场能量平分角。
φ的值可通过测量装置内部参数求解:
(5)
联立式4~式5,得到平分投影点的坐标为
(6)
工件偏转角β初值为0,当工件表面与入射光不垂直时,工件偏转角β改变,即β≠0,此时接收屏上质心位置偏移坐标为
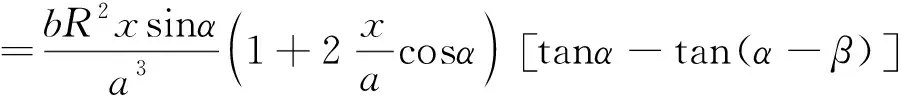
(7)
根据偏转工件光学几何关系,求解工件偏转引起的距离偏差Δx为
(8)
实际测量过程中的误差补偿,需采用多组数据来提升补偿的精度。因此,将偏转角模型区域和误差值组合,构建多项式补偿方法(见图4)。
首先,根据被测工件实时偏转角γ,基于装置内部几何关系,可得到偏转角模型关系表达式为
dt=tanγ-tan(anglefix-γ)
(9)
式中,anglefix为测量装置内部固定夹角,可通过实测结果和数模获取数据差,然后分析模型原始数据对齐结果,计算每一测量段的角度对应值:

图4 多项式补偿方法流程图
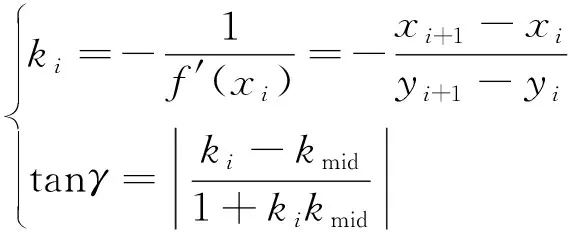
(10)
式中,ki为法向量;f′(xi)为原始数据曲线切向量;kmid为模型零偏移点法向量。
接下来,获得全局参数的数据验证模型ΔD为
ΔD=Hn.dt
(11)
式中,Hn为多项式变换矩阵,n为拟合项的阶数。考虑到效率和实际应用情况,一般选取5阶以下多项式进行数据拟合,选取大量先验试验数据,并进行模型验证,最终获得对应误差补偿模型及补偿结果。
4 试验验证
为了验证提出的基于工件偏转角的激光线扫描误差补偿方法的有效性,首先采用三坐标平面定位试验来求解安装定位初始偏差,同时通过提取非标准量块和哑光陶瓷标准靶球的局部点云数据分别从定性、定量的角度分析工件偏转误差补偿效果。试验布局如图5所示。
采用三坐标测量夹具端面,完成平面定位,S型扫描点云得到夹具平面位姿信息。采用平面拟合法,求解对应平面关系式。针对各个坐标轴之间的位置关系,分别对实际情形下夹具坐标系与平移台理想坐标系对应角度的误差矩阵进行对比和验证。此外,通过激光线扫描仪在工件表面投射激光并实现等步长扫描表面位置信息,对测量数据进行重建与补偿,从而提取优化结果及模型真值,对比重建前后特征信息值的均方差。
基于Ransac方法,对曲面坐标分层后进行数据降维,剔除每条曲线对应的坐标误差,最后得到最优目标数据,曲面扫描结果如图6所示。


图5 试验布局图

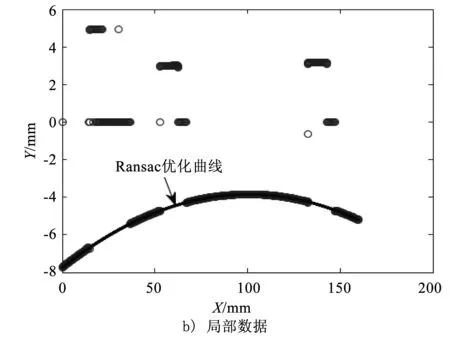
图6 曲面扫描结果
基于所提出的工件偏转误差补偿方法,设计试验方案以验证工件表面倾斜角误差及补偿模型的有效性。首先,将激光线扫描仪水平安装在移动平台上,确保入射光束方向的一致性,同时将标准靶球和非标准量块固定在可升降平台上。标准靶球直径为25.385 mm,非标准量块的曲率为1 305 mm。将位移平台在零点时线扫描仪的测头位置设为坐标系起点,设置单轴运动采样步长为0.02 mm,总测量距离为160 mm,共测量8 000列数据点,每一列包含800个数据点。将测量数据曲线与被测模型原始曲线进行对比,对比结果如图7所示。


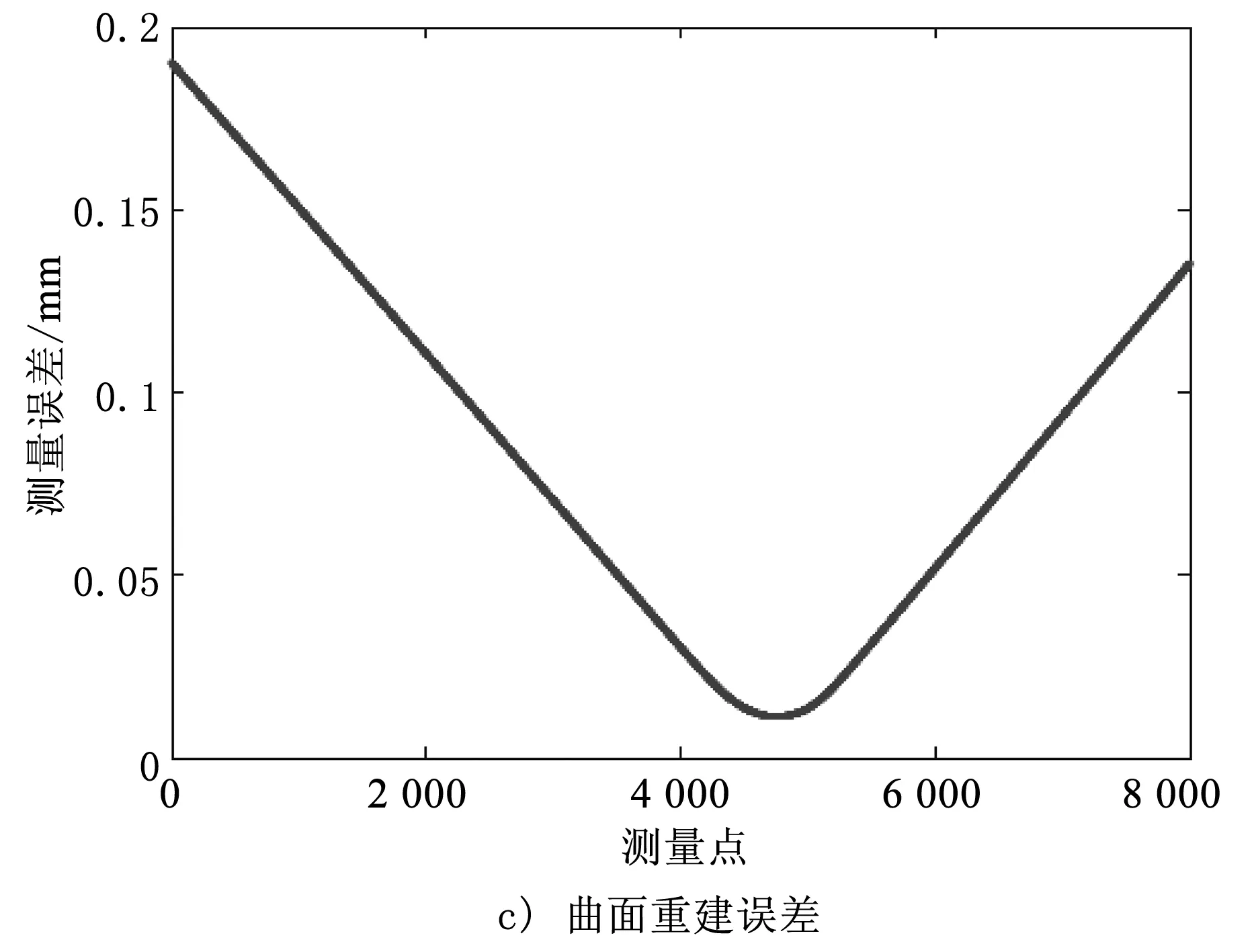
图7 重建模型对比结果
基于多组测量数据的重建特征,求解曲面重建误差的均方根值和6组靶球重建的补偿结果,重建试验对比结果如图8所示。
由图8可知,经过补偿后重建的测量曲线优于原始测量曲线。经过计算,补偿后的靶球测量误差减少了77%,拟合目标半径平均误差均方根值低于10 μm,补偿后的曲面测量误差平均降低了75%,均方差低于0.05,因此,所提出的补偿方法可有效降低测量误差。

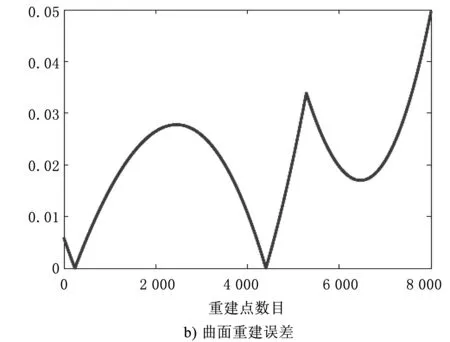
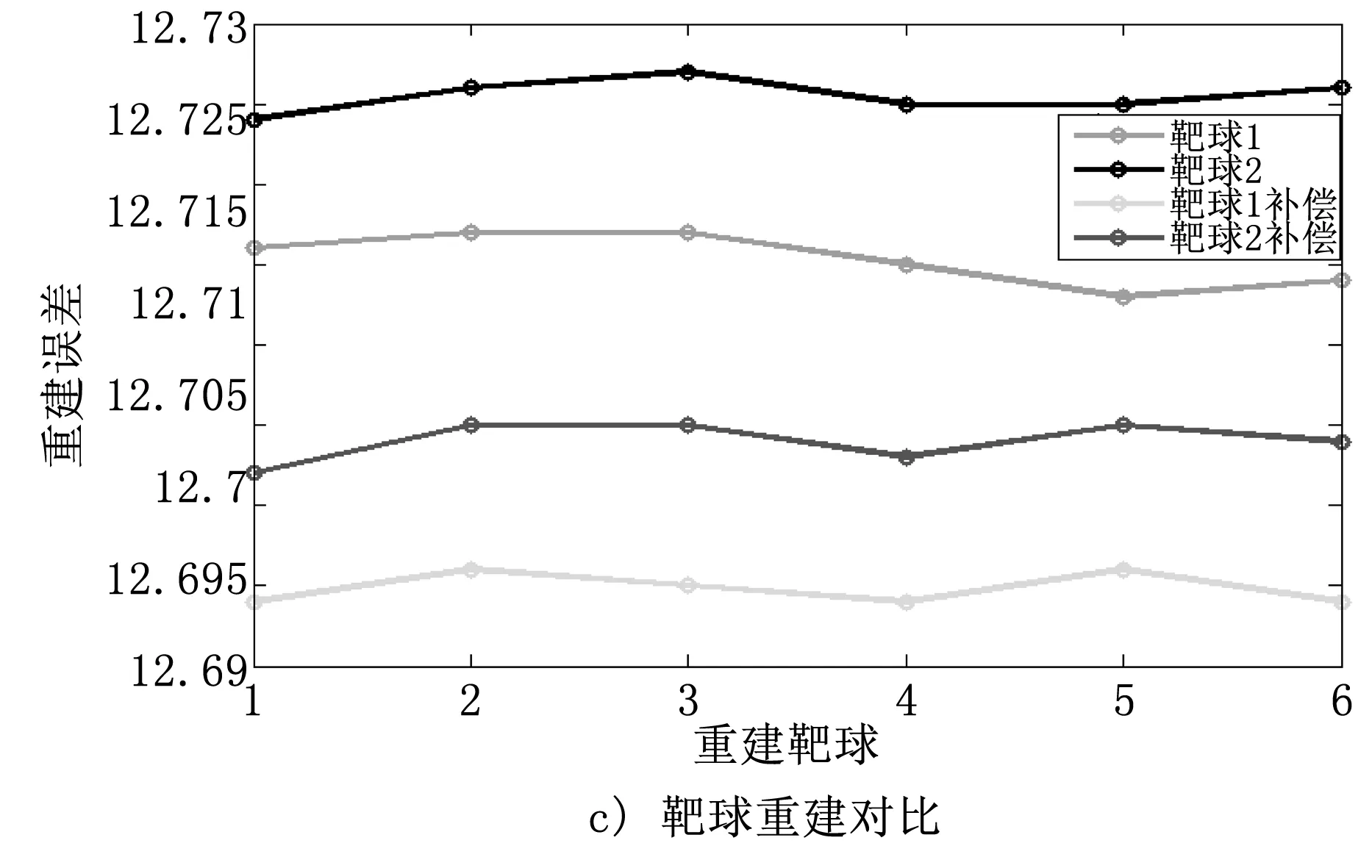
图8 重建试验对比结果
5 结语
所提出的局部三维坐标测量方法,通过Ransac数值优化获取满足局内要求的特征点云,针对存在的系统误差情况,提出了基于工件偏转角的激光线扫描误差补偿方法,采用安装角和数模配准,对误差进行了溯源和优化。该补偿方法计算效率高,能够实现大批量点云数据的快速精确补偿,同时,针对标准靶球和非标准量块表面特征开展了多组提取试验,结果表明具有较好的误差补偿效果。
