低压断路器主回路温度场仿真分析

伍 轩，李 蕊

（武汉船用电力推进装置研究所，武汉 430064）

0 引言

断路器正常工作时，主回路长时间通以额定电流会产生大量焦耳热，热量一部分散失在周围介质中，另一部分使断路器各部件温度升高。过高的温升会破坏断路器的绝缘性，或使其工作寿命严重降低，或使其内部结构机械性能降低，产生安全风险[1]。采用数值方法对断路器温度场进行仿真分析有助于避免设计缺陷，指导优化断路器内部结构，还有助于节约成本，缩短设计周期。为了简化处理，工程上一般采用牛顿热公式估算电器的发热，但误差较大。本文对断路器主回路的发热和散热进行分析，根据实测接触电阻反向建立导电桥模型，整合了对流散热系数和辐射散热系数，用ANSYS对断路器主回路温度场分布进行仿真，并通过实验进行验证。

1 断路器主回路温度场分析模型

1.1 研究对象

本文分析的对象为额定电流为200 A的双断点交流断路器。由于发热源为主回路，断路器的其他结构只起热传导作用，因此模型上可以进行简化。图1为断路器的主回路模型。

图1 断路器主回路模型

1.2 热传递数学模型

热量传递有三种形式，导热、对流和热辐射[2]。断路器额定状态工作时，主回路产生的热量通过这三种形式散失到周围介质中。在断路器内部，由于空气对流缓慢，只考虑导热和热辐射，忽略对流的影响。对断路器外壳、外露的部件和外接导线则考虑对流散热和辐射散热的影响，并通过表面散热系数来简化。

为便于计算作如下基本假设：塑壳断路器处于无限大空间；材料各向同性；环境温度不变，为实验时测得的室温。

因此稳态时断路器内部的三维热传导方程为：

式中：T—物体的温度，K；γ—导热系数，W/(m·K)；q—单位体积内热源的生成热，W/m3。

断路器内部零件、外壳表面、外露部件和外接导线的边界散热条件为：

式中：α—表面散热系数，W/(m2·K)；T0—发热体温度，K； Tf—周围环境温度，K。

式（1）、（2）为断路器的热分析模型，利用有限元软件（ANSYS），结合主回路发热功率、各部分材料导热系数和表面散热系数，即可对断路器的稳态温度场进行仿真计算。

2 断路器主回路热源分析

断路器额定状态工作时，主回路发热源于电流流经回路自身的电阻、动静触头的接触电阻和外接导线的接触电阻。计算发热功率需获取主回路各部分电阻值和电流密度。

由于动静触头之间、外接导线与接线端之间存在接触电阻，电流流经接触部位时发生收缩，电流密度增大，功率损耗增加，使接触部位的发热比其他导体部位更加明显。因此计算主回路温度场分布时，必须考虑接触电阻的影响。

2.1 导电桥模型的建立

动静触头之间的接触电阻可视为串联在动静触头之间的电阻，并假设接触表面的所有导电斑都集中在中心部位形成一个较大的导电斑，利用一个圆柱形的导电桥来模拟动静触头间的电接触[3]，如图2所示。

图2 导电桥模型

导电桥的半径与触头终压力和触头材料有关，其接触半径可按下式计算：

式中：F—触头终压力，N；H—接触硬度，N/mm2，约为材 料布氏硬度的60%～80%；ε—修正系数，取0.3；

由于导电桥尺寸直接影响流经导电桥的电流密度，为控制导电桥发热功率，必须确定导电桥的高度尺寸。可通过实测回路压降，对导电桥高度，可按下式计算：

式中：ΔV—回路压降，V；I0—额定电流，A；R—各零件在回路中的电阻之和，Ω；n—导电桥数量；ρ0—触头材料电阻率；k—高度系数，取0.67；

2.2 接线端接触电阻的确定

接线端的存在会对温升产生影响，其电阻大小由两侧接触物体表面状况以及螺栓紧固效果共同影响，接触面氧化明显或螺栓紧固程度不佳，都会造成接触电阻过大，发热加剧，进而影响断路器主回路的温度场。

在接线端子和外接排之间建立一片薄膜，利用此薄膜来模拟接触电阻的作用。接触电阻可按下式进行计算：

式中：m—与接触形式有关的系数，平面接触时取1，曲面与平面接触时取0.5；Fk—接触力，N；cρ—接触材料系数，Ω·Nm；

3 表面散热系数的确定

3.1 断路器表面散热系数的确定

断路器外壳外表面，与外部空气接触的表面，其散热由对流和辐射散热组成。

1）对流散热可表示为：

式中：q—热流量，W；αcon—对流散热系数，W/； A0—对流散热面积，m2。

边界的散热系数和周围流体的特性相关，对于自然对流换热，根据努赛尔特（Nusselt）相似准则和相关的关联式有[4]：

式中：Gr—格拉斯霍夫数；Nu—努塞特数；Pr—普朗特数；g—重力加速度，m2/s；αv—体胀系数，K-1，为温度倒数；v—气体运动黏度，m2/s；Δt—壁面与流体温度之差，K；l—为特征长度，m；γ—为空气导热系数，C，n—常数，取值分别与散热面特征和流体状态有关；根据断路器表面的尺寸和流体的物性参数即可计算出相应的对流散热系数。

2）辐射散热，根据Stefan-boltzmann定律，可表示为：

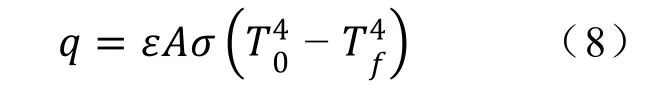
式中：A—辐射面外表面积，m2；ε—外表面发射率；σ—斯忒藩-玻尔兹曼常量，W/(m2·K4)。

分析时，辐射散热可通过表面散热系数简化：

因此表面散热系数可整合为：

3.2 外接导线表面散热系数的确定

在对断路器进行数值热分析时，外接导线的散热作用十分明显，必须考虑。根据国标，通过200 A额定电流时，导线的截面积为95 mm2，连接长度为2 m。外接导线处于空气中，通过对流和辐射散热，同时导线中通入电流会导致自身温度升高。裸导线的对流散热系数为：

式中：d—连接导线直径，mm；

联立式（9）、式（10）求得导线的总散热系数α。绝缘层对导线的散热有不可忽略的影响，根据国标，通过电流200 A导线的绝缘层材料为PVC，且厚度不小于1.6 mm。导线的散热系数需按下式修正[5]：

式中：ra，ri—加绝缘和裸导线的半径，m；λiso—绝缘材料的热导率，W/(m·K)；

4 结果与分析

4.1 仿真结果

在ANSYS中设置材料属性，外壳和罩壳赋予DMC塑料，触头赋予银钨合金，其余部分统一赋予铜，并按表1赋予对应的导热系数。

表1 材料导热系数

使用ANSYS软件，通过热电直接耦合模块对塑壳断路器在额定通流200A情况下的主回路进行温度分布仿真。按式（10）计算各表面散热系数，对于断路器外壳、外接导线等裸露在外的部分考虑对流和辐射散热系数，对于断路器内部零件只考虑热传导和辐射散热系数。环境温度为26.5℃。主回路的温度场分布如图1.3所示。图中标识的1～6为实验时测试温度的点，测量点1、4对应A相的进出线端，2、5对应B相，3、6对应C相。

图3 断路器主回路温度仿真结果

如图3所示，对于主回路的每一相，由于动静触头处接触电阻的存在，触头处的温度较导体其他部位高，且由于是双断点结构，触头中间部位温度最高；三相比较可见，B相温度较A、C两相高，这是由于B相位于中间，不仅A、C相的热源对其有加热作用，且散热条件也不如紧贴外壳侧壁的A、C相。从仿真结果来看，接线端平均温升在40K左右，触头温升在55 K左右，满足国标低压电器极限允许温升要求。

断路器主回路电位分布如图4所示。图4可以看出，主要的压降出现在导电桥部分，也进一步说明，动静触头间的接触电阻是主回路发热的主要热源。

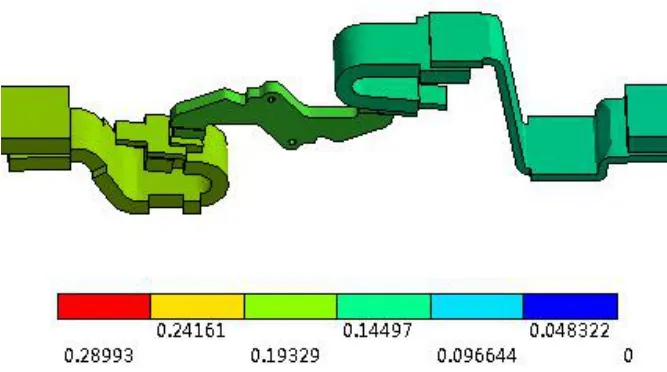
图4 断路器主回路电位分布

4.2 试验验证

为验证仿真计算的正确性，根据国家标准GB/T 14048.1-2000，给主回路通电进行实验，在标识点1～6处分别粘贴热电偶，用长2 m截面积为95 mm2的导线将ABC相并联，采用电流调压器给各相主回路通200 A电流，达到稳定温升后，用热电偶测量标识点处的温度。

测试点温度的计算值和实测值比较如图5所示，其中测试点1～6与标识点1～6对应。

图5 温度场计算与实验结果比较图

由图5可知，测试点1温度低于测试点3，且温差达到了6.2 K，相对测试点1温度误差约为10%，实验结果表明A、C相之间温度不平衡。这可能是由于断路器合闸时，由于装配误差和配合间隙等原因，造成不同相的动静触头终压力不同，C相的触头终压力较大，其动静触头间的接触电阻较小，因此在相同的电流下发热量较小。计算值与实测值之间误差大小如表2所示。从表中可以看出，测试点误差均在可接受范围内。

表2 计算值与实测值误差大小

测试点1、2、5实测温度大于计算温度，这可能是由于该处与外接导线之间的螺栓连接不够牢靠、连接时接触表面不够清洁，导致此处接触电阻较大，发热量大于计算值。

5 结论

基于断路器主回路的热分析模型，通过简化断路器和外接导线的散热系数，对断路器主回路的稳态温度场进行仿真分析。提出了依据实测动静触头的接触电阻建立导电桥模型的方法。通过对比仿真与实验结果，验证了仿真分析的正确性。