一种改进的基于RSSI测距的室内三维修正定位算法

徐 进，李时铭，谢建中，杨栋梁，张丙钊

（武汉船用电力推进装置研究所，武汉 430064）

0 引言

近年来，无线传感器网络技术发展迅速，广泛应用于矿井人员定位、抢险救灾、环境监测、智能家居等领域，对人们的生活和工作产生了重大的影响。

当前，大多数定位算法只是针对无线传感器的二维网络展开研究的，在实际应用中并非总是如此。无线传感器网络节点也会经常处于三维环境中，如矿井、森林、海洋和复杂的建筑物等，这些场合下需要提供节点的三维位置信息。

三维空间运算更加复杂，三维定位技术的研究还有待深入。目前已有部分关于三维定位算法研究的文献。为了提高定位精度，大多数算法采用增加节点数量，提高成本来实现。但如果控制成本，减少节点数量，则运算量会增加，且定位误差较大。本文提出了一种节点数量少，定位误差小的基于RSSI的改进三维修正定位算法。

1 RSSI测距模型

1.1 室内无线信号传播模型

在实际应用环境中，由于多径、绕射、遮挡物等因素，采用对数-常态分布模型将更加合理[1]。对数-常态分布模型如下：

式中：PL（d）为经过距离d后的路径损耗；PL（d0）为自由空间损耗，d0为参考距离，常取1 m；Xδ为平均值为0的高斯分布随机变数；n为路径损耗因子。

RSSI测距模型如下：

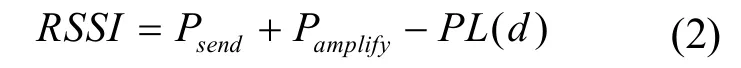
式中：RSSI是接收信号强度指示；Psend是发射信号的功率；Pamplify是天线的增益。

将模型简化，可表示为：

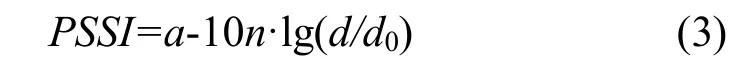
式中：a=Psend+Pamplify-PL(d0)- Xδ，由(3)式知，RSSI与 10·lg(d)成线性关系。

1.2 校正传输参数

由于室内定位存在许多干扰因素，如反射、多径效应、物体遮挡、气候等，使定位难度十分大，如果直接采用上述 RSSI测距模型进行定位，则难以达到室内定位要求的定位精度。所以，校正当前环境的传输参数是十分重要的[2]。

根据RSSI测距模型可以得到：

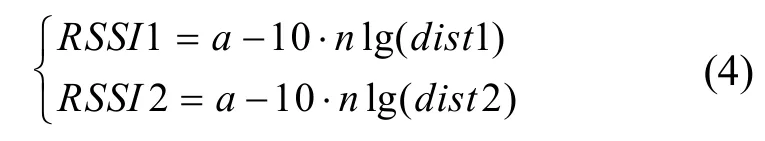
解方程组(4)，可以得到路径损耗因子n：

将n代入方程组(4)中，可以得到参数a：

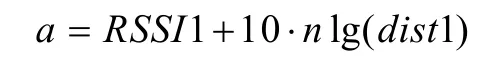
2 算法说明

2.1 定位解算

假设 4个参考点坐标分别为A(xA,yA,zA)，B(xB,yB,zB)，C(xC,yC,zC)，D(xD,yD,zD)，未知节点的坐标为M(x,y,z)，节点M到A、B、C、D点的测量距离分别为dA,dB,dC,dD，根据三维空间计算公式，可以得到式（5）超定非线性方程组：对此超定非线性方程组，本文采用最小二乘法和牛顿迭代法进行求解。

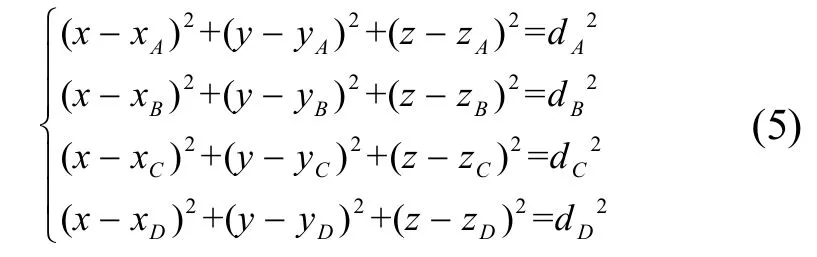
2.1.1 最小二乘法

将上述超定非线性方程组转化为线性方程组形式AX=b，其中：

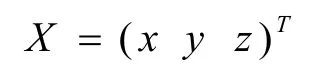
根据最小二乘法，当矩阵AT A为非奇异矩阵时，可求解出未知点M的最优估计坐标值[3]：

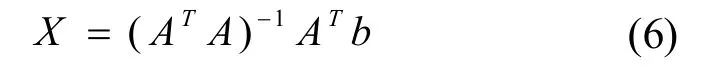
传统的最小二乘法三维定位算法则是直接利用最小二乘法求解方程组进行最终定位。当前的大多数基于RSSI的三维定位算法也是利用最小二乘法解方程组的。

但是当所有参考节点均分布于同一高度时，rank(A)＜3,最小二乘法将无法解出答案。

2.1.2 牛顿迭代法

将方程组(5)转化成以下形式：

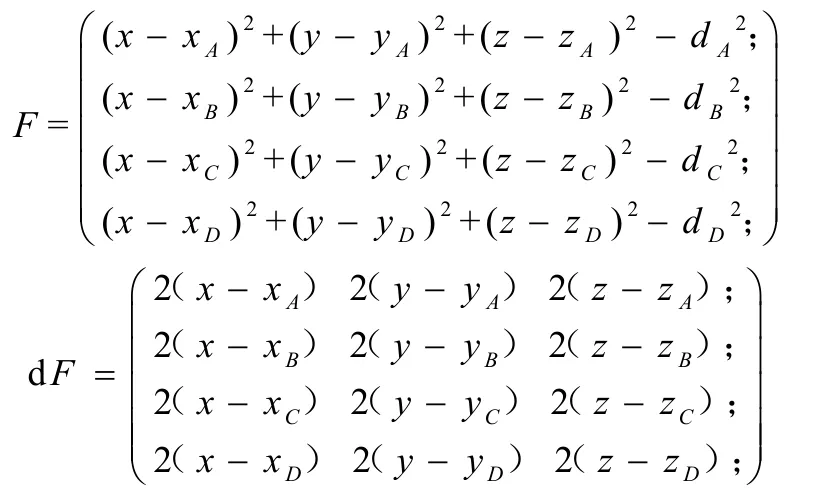
牛顿迭代法的迭代公式如下：

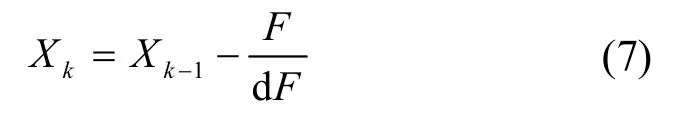
Xk为经过迭代k次后，所得到的一组解。但是牛顿迭代法的收敛性依赖于初始值，选取不同的初始值可能会得到方程不同的根[4]。所以寻找一个好的初始值十分关键，这需要不断的尝试。

无论参考节点是否分布于同一高度，牛顿迭代法都可以得到一组近似解。但是参考节点不能放置于中间高度的同一水平面，必须放置于最底面或最高面。因为同一水平面的参考节点对于三维定位就已经减小了参考作用，当它们在中间高度的同一水平面时，难以根据测量距离判断未知节点是在此水平面的上方还是下方，易导致z轴方向定位误差大。

2.2 改进的三维修正定位算法

改进的三维修正定位算法是在定位解算原理的基础上，增加了修正传输参数、差分修正、迭代次数等环节，对未知节点进行进一步的修正定位，减小室内干扰因子的影响。

此定位算法中只需要A、B、C、D、E这5个已知相对坐标的参考节点依次作为差分修正参考节点，对未知节点M进行定位[5]。具体步骤如下：

步骤一：参考节点A、B、C、D、E根据接收到其它参考节点的RSSI值，由公式（7）、（8）分别计算出自身作为差分修正参考节点时相对应的校正参数a和n。

其中ni、ai分别表示第i个参考节点作为差分修正参考点时所对应的路径损耗因子及传播参数，j则表示第j个参考节点作为修正节点，m则表示第m个参考节点作为辅助修正节点，其中i,j,m= 1,2,3,4,5，且i≠j≠m；dist(i,j)表示参考节点i到j的距离；表示测量到的参考标签j到i的RSSI的平均值。

步骤二：B、C、D、E对差分修正参考节点A进行初步定位，并得出偏移量(ΔxA,ΔyA, ΔzA)。

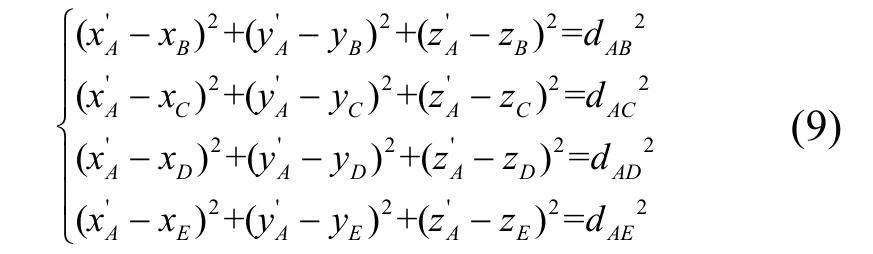
其中dAB,dAC,dAD,dAE分别表示A点到B、C、D、E的测量距离。可以利用最小二乘法或牛顿迭代法解此超定非线性方程组，得到 A定位坐标，然后与 A的实际坐标相减，便可以得到偏移量(ΔxA,ΔyA,ΔzA)：

步骤三：利用B、C、D、E参考节点对未知节点M进行初步定位，得到。

其中dMB1,dMC1,dMD1,dME1分别表示M点到B、C、D、E的测量距离。根据方程组(11)可求解到修正参考坐标 (xMA1,yMA1,zMA1)。

同理，分别以B、C、D、E作为差分修正参考节点对M点定位，便可以得到节点M的修正参考坐 标。差分修正的目的是对当前环境下初步定位的进一步修正。

步骤四：加入迭代次数r，求得各个差分修正参考节点的所对应的r个修正坐标，然后分别取其均值：

迭代次数的应用减小了个别误差较大点对最终定位的影响力，有助于减小定位误差。

步骤五：利用加权算法[6]计算出M点的最终定位坐标(x,y,z)，如下式所示：

将测量距离均值的倒数和作为权重，这更好地体现了各个差分参考节点对未知节点的定位影响力。

步骤六：利用公式(16)，计算出定位误差：

其中，(xM,yM,zM)为目标点的实际坐标。

3 仿真结果

仿真条件是在一个10m·10m·10m的三维区域内，放置5个参考节点，其坐标已知.未知目标节点的坐标由matlab随机生成函数来生成，在该区域内随机分布，一共生成10个未知目标节点.然后根据RSSI值与距离的关系，由（1）、（2）、（3）式生成RSSI数据，并在数据中添加均值为0，标准差δ为3的高斯噪声，作为RSSI的随机分量，以模拟实际环境中的反射、多径效应、物体遮挡、气候等带来的影响.路径损耗因子n的初始值n0=4，传播参数a的初始值a0=-46.当参考节点分布在不同高度的情况下，分别对传统最小二乘法定位算法和改进定位算法进行仿真；参考节点处于同一水平面时，对使用牛顿迭代法的改进算法进行仿真.以下为参考节点的分布位置表及仿真结果。

表1 参考节点坐标分布

从图1，2，3可以看出，在参考节点处于不同高度的情况下，改进后的三维定位算法的定位精度明显比传统算法的定位精度高。从表2可知，改进后的三维定位算法的平均定位误差为0.3873 m，比传统算法的平均定位误差1.2691 m小.仿真结果综合说明改进算法的定位精度有明显提高.但是当参考节点处于同一高度时，改进的定位算法的定位误差仍较大，定位误差接近1 m。

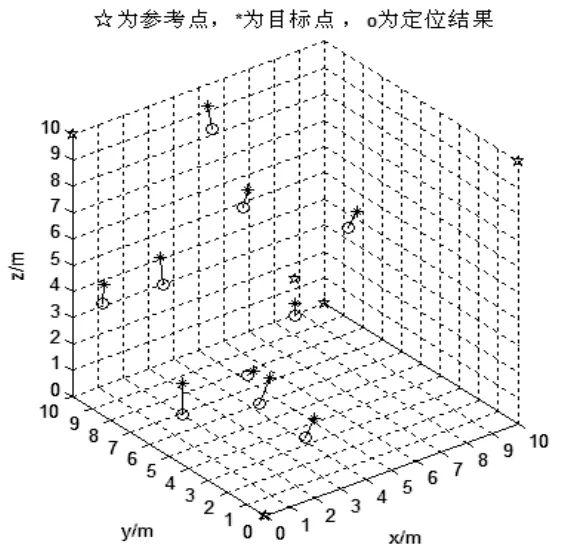
图1 传统三维定位效果图

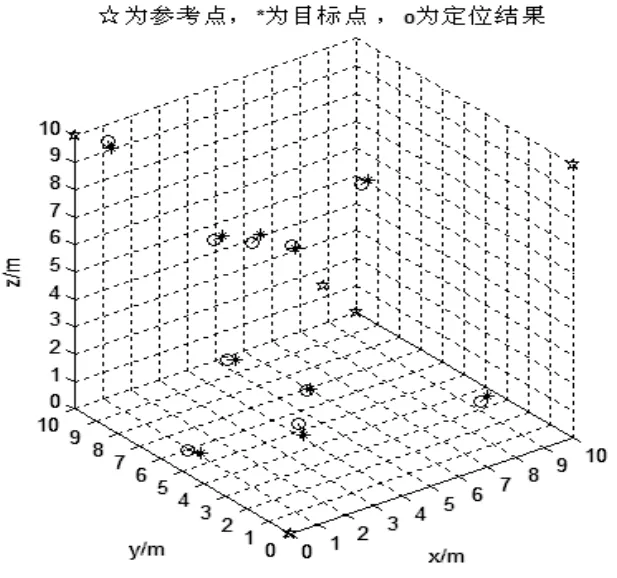
图2 改进算法的三维定位效果图

图3 同一高度的改进算法三维定位效果图

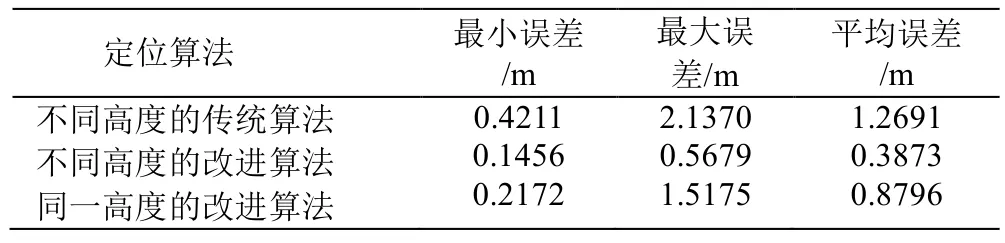
表2 定位误差比较

4 结论与展望

该算法在不增加额外参考节点数量的情况下，利用参考节点对当前环境的传播参数进行了初步校正，同时也加入了差分修正、迭代次数和加权算法等环节，对定位坐标进行进一步修正，大大提高了定位精度。但是在实际应用中，参考节点应均放置于最顶层，这样减小了多径作用和遮挡物的影响，通过仿真结果可知，定位误差较大，还有较大的改进空间。