基于增殖放流的定栖性种类剩余产量模型及其模拟分析
2021-03-15王迎宾
王迎宾
(1.浙江海洋大学 水产学院,浙江 舟山 316022)
1 引言
在不断增加的捕捞强度的影响下,渔业资源遭受着过度捕捞的压力,资源的可持续利用面临挑战[1]。随着渔业生物育苗和养殖技术的快速发展,人类已经可以通过采取增殖放流等人为介导手段,大规模地对自然生态开展人工干预。从最初单纯以增加商业捕捞对象资源量为目的增殖放流,到如今以构建健康的半人工生态系统为目的海洋牧场建设,使渔业资源得以延续。国际《海洋科学百科全书》对“海洋牧场”有一个简单而明确的定义[2−3],即海洋牧场通常是指资源增殖。由此可见,海洋牧场的建设与管理离不开资源增殖。但与最初的仅以增加产量为目的的增殖放流有所不同,如今人类对人为介导所产生影响的关注也逐渐延伸到资源的可持续性,例如,海洋牧场海域内增殖目标种的最可持续产量(Maximum Sustainable Yield,MSY)水平,就是众多学者和牧场经营者十分关注的问题之一。
MSY 被定义为在一定的海域范围内和现有环境条件下,可以连续获得的最大平均产量,长期以来一直被全球许多渔业视为重要的管理目标。20 世纪50 年代,随着剩余产量模型的发展,MSY 被广泛使用,其概念在1982 年《联合国海洋法公约》中被采纳,而且作为法律条款写入诸多渔业发达国家的渔业法规当中,许多国际组织也将MSY 作为主要的管理目标之一。剩余产量模型自提出之时,就受到了广泛欢迎,很多学者也对传统模型进行了完善和改进。Thiaw 等[4]将上升流等环境因子加入剩余产量模型,对塞内加尔白虾(Penaeus notialis)资源进行了评估。Reid 等[5]使用基于状态空间的剩余产量模型,估算了尼皮贡湖白鲑(Coregonus clupeaformis)的主要生物学参考点。Shibata 等[6]提出了对传统剩余产量模型进行了调整,并基于此分析了季节间在两个区域来回游动的渔业资源的产量变化。然而从生物群体角度看,传统的以及上述改进的剩余产量模型均只考虑了生物群体自身的繁衍,而无法解决像海洋牧场中受增殖放流影响较大的生物群体MSY 的估算问题。针对这一问题,国内外至今尚未见到有相关研究报道。
海洋牧场海域界限比较清晰,并且其中的定栖性种类移动性较弱,使得资源的环境容纳量相对稳定。相反,开放海域生产作业的边界不够明确,而且在实施增殖放流后,放流种类的栖息海域可能有所扩展,特别是游动性较强的种类,从而使研究海域的环境容纳量难以确定。因此,本研究针对海洋牧场海域定栖性种类,建立适用于增殖放流影响下的剩余产量模型,并通过模拟,估算不同增殖及捕捞策略下MSY 的评估结果,以期为增殖放流背景下的资源可持续利用提供理论依据。
2 材料与方法
2.1 模型
剩余产量模型是现代渔业资源评估和管理的主要理论模型之一,其将每年种群的生长、补充和自然死亡结合起来作为种群的年剩余产量,表示除了捕捞以外的种群年综合生产力,因此捕捞和剩余产量是影响种群生物量的两个因素[7]。Schafer 提出的剩余产量模型,是最早被广泛采用的产量模型,该模型假定生物量增长率与生物量的关系服从逻辑斯蒂(Logistic)分布[8−9]。它的具体公式为

式中,Bt表示第t年的资源生物量;r为内禀增长率;K为环境容纳量;Ct表示第t年的产量。
在非平衡状态下,离散型剩余产量模型的一般形式为

当不考虑捕捞时,上述模型通过r来实现群体自身的逻辑斯蒂增长,即生物量的年际增长服从S 型曲线(图1)。当考虑捕捞时,人们希望找到能保证生物量可持续时的最大产量,即MSY。上述模型中,r表征的是资源栖息海域生物量的自身增长,也就是生物通过自身繁殖、生长等作用,呈现出的生物量增长率。因此,当有外部因素介入,例如增殖放流,上述模型就有局限性了。因为放流的个体虽然也增加了群体的生物量,但其增长特征无法用表示群体增长率的r进行描述。因此,须在公式(2)中引入其他参数,表示增殖放流对群体生物量变化带来的影响。
基于此考虑,在公式(2)的基础上加入描述增殖群体增长特征的参数—有效增殖率(e),用以表示增殖放流的群体生长至可捕捞规格的生物量比例。于是,得到增殖剩余产量模型公式
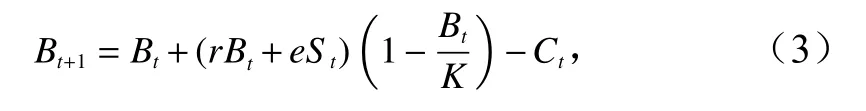
式中,Bt表示第t年原存群体(海域原本存在的群体)生物量;St表示第t年增殖放流苗种全部长到可捕成体规格时的生物量。该模型将海域中原存群体与增殖群体对生物量的影响分开考虑。因为增殖群体并未改变原海域对生物固有的容纳能力,所以模型中的K值大小并未改变。因此,该模型的曲线将同样呈现S 型,并趋于同样的极值。

图1 海洋牧场刺参(Stichopus japonicus)增殖模拟生物量和产量变化Fig.1 Simulation changes of biomass and yield of Stichopus japonicus enhancement in marine ranching
2.2 模拟分析
为了分析增殖剩余产量模型在不同增殖放流策略下的使用效果,本研究基于增殖定栖性种类刺参(Stichopus japonicus)的资料进行模拟研究,主要考虑定栖性种类活动范围小,生活边界比较清晰。明确的生活范围边界,是剩余产量模型应用的前提,估算得到的MSY 与该范围也是相对应的。因此,以定栖性种类为例,所分析的问题比较简单,误差也相对较小。
增殖刺参群体20 年的生物量和产量的变动过程如图1 所示。基于增殖剩余产量模型,模拟比较无增殖放流和每年增殖放流量稳定的情况下,产量与生物量,以及产量与捕捞努力量之间的关系。对于每种增殖策略,分析其MSY、捕捞努力量(EMSY)和生物量(BMSY)的变动特征。同时,对于不同水平的年增殖放流量(0.36 t、0.48 t 和0.60 t),以及年增殖放流量持续变动的情况,也进行了模拟分析,用于对比。模拟使用相关参数如表1所示。
为了探讨不同捕捞强度对增殖剩余产量模型评估结果产生的影响,在不同增殖放流数量基础上(年增殖放流量稳定、持续增加、持续减少和随机4 种增殖策略,增殖放流均从第8 年开始,相关参数如表1所示),基于现实捕捞努力量和产量数据,模拟形成了产量的3 种变化趋势,即持续增加、持续下降和先增后降(图2)。考虑到产量和捕捞努力量的观测值可能存在误差,在模拟过程中对产量和捕捞努力量均加入随机误差,ε~N(0,σ2),其中σ等于产量或捕捞努力量均值的10%。模拟中参数的估算使用观测误差法,每种增殖策略和捕捞策略情况均模拟重复1 000 次,然后绘制箱型图来呈现模拟结果的分布情况。
3 结果
3.1 模型的特点与参数求解
与传统的Schaefer 剩余产量模型相比,增殖剩余产量模型增加了1 个参数和1 个变量,即有效增殖率e和年增殖放流苗种全部长到可捕成体规格时的生物量S。增殖剩余产量模型是在Schaefer 模型基础上提出的,因此其适用条件和假设与传统模型既有相似之处,也有所不同。首先,在有限生态系统中,资源群体的资源生物量可增长到接近该生态系统的最大容纳量,并且该容纳量不因增殖放流而发生变化;第二,环境容纳量接近于初始资源群体;第三,生物量的增长服从逻辑斯蒂的S 型曲线模式;第四,增殖放流群体与海域中原存群体之间会产生抑制作用,每年增殖放流量越大,原存群体的最大容纳量越小,同时原存群体的MSY 以及相应的EMSY越小。根据增殖剩余产量模型计算得到的生物量年际变化曲线虽然呈现出S 型,但与公式(2)的曲线相比,其曲线逼近极值的速度加快了,生物量增长率(dBt/dt)的拐点也提前出现(图3)。由于增殖剩余产量模型的结构与传统的生物量逻辑斯蒂生长模型相比有所变化,其相应的一些关键参考点计算公式也有所改变。MSY 表示在保证资源可持续利用的前提下,每年可获得的最大产量。因此,增殖剩余产量模型需满足

表1 以刺参(Stichopus japonicus)增殖为基础的海洋牧场定栖性种类模拟参数Table 1 Simulation parameters of Stichopus japonicus enhancement in marine ranching
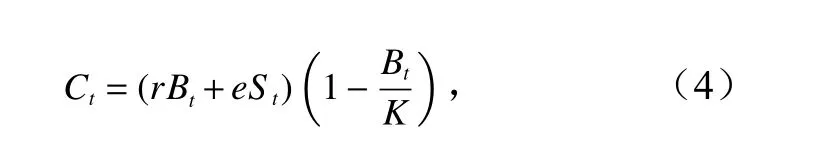
在每年增殖放流量稳定的前提下,将产量对生物量求导,并令其等于0,即


图2 模拟4 种捕捞努力量和产量的变化趋势Fig.2 Trends of fishing effort and yield of the four simulated scenarios
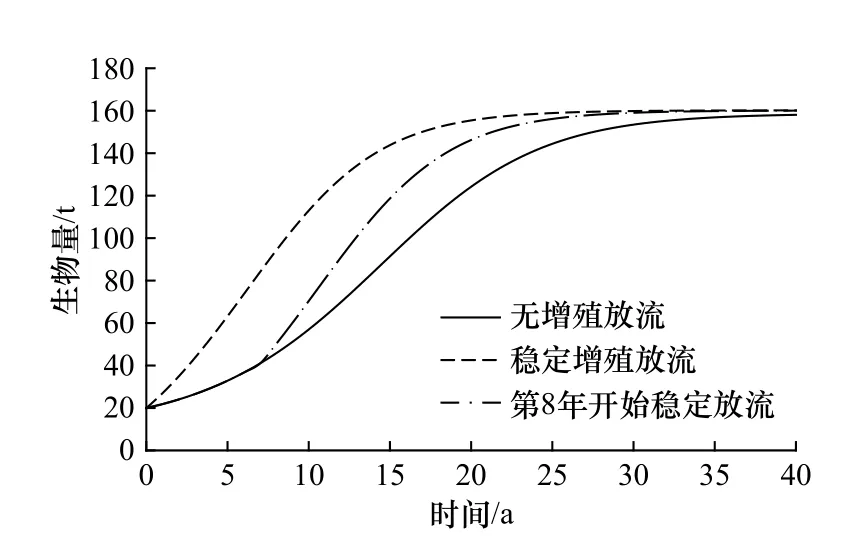
图3 有无增殖放流情况下渔业资源群体逻辑斯蒂增长示意图Fig.3 Schematic diagram of logistic growth of fishery stock with or without enhancement
则

此时,对应的MSY 的计算公式为

可见,与传统的Schafer 剩余产量模型相比,使用增殖剩余产量模型求算的MSY,除了与参数r和K有关,还受到增殖放流的影响。换言之,可将增殖放流背景下的MSY 视为来自两个方面,即海域原存群体和增殖放流群体。
对公式(4)进行变换得到
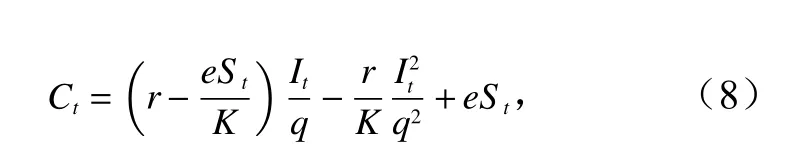
式中,It表示第t年的CPUE;q表示可捕系数。进一步变换得到

在此设定公式(10)等于0,即意味着dBt/dt=0。当每年增殖数量稳定,并且给定每年的捕捞努力量大小时,公式(10)便是1 个一元二次方程,可以计算得到dBt/dt=0时的产量,即给定年增殖放流数量和捕捞努力量时的MSY 值。这样,可以在固定每年增殖放流数量情况下,通过设定不同的捕捞努力量,得到年增殖放流量一定时的MSY 及对应的EMSY。相反,同样可以固定每年的捕捞努力量,而设定不同的年放流量,此时的持续产量和对应的捕捞努力量将随着年增殖放流量的增加而持续升高。
由此可以知,增殖剩余产量模型对应的MSY 曲线将不再是公式(2)得到的抛物线,而是1 条偏态曲线。其中,产量与生物量的关系曲线为负偏态(图4),而产量与捕捞努力量的关系曲线为正偏态(图5)。表示在增殖放流背景下,获得MSY 时的生物量低于无增殖放流时的情况,而获得MSY 时的捕捞努力量则高于无增殖放流时(图4,图5)。图4 显示,增殖剩余产量模型的曲线与纵轴的交点大于0,即理论上即使海域中该渔业资源的生物量为0,也可以依靠增殖放流获得一定的产量。由图5 可知,当产量达到MSY后,继续增加捕捞努力量,由于增殖放流对生物量的补充作用,持续产量曲线下降速度较为缓慢。图4 曲线中对应的BMSY和MSY 可使用公式(6)和(7)计算得到,而图5 中曲线中的EMSY可通过求解公式(10)中Et的解而得到。当无增殖放流时,取St=0 即可。
公式(6)和(7)中相应参数的求解方法与传统模型相似,可以使用观测误差法或者过程误差法。其中观测误差法假设生物量动态变化模型是准确的,误差出现在单位捕捞努力量渔获量的观测值上,其参数求算过程如下:


图4 有无增殖放流情况下产量−生物量关系示意图Fig.4 Schematic diagram of the relationship of yield-biomass with or without enhancement

图5 有无增殖放流情况下产量−捕捞努力量关系示意图Fig.5 Schematic diagram of the relationship of yield-fishing effort with or without enhancement
过程误差法假设各观测数据是准确的,误差源于生物量动态变化模型,参数求算过程如下:
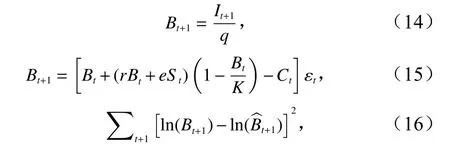
公式(13)和(16)分别为观测误差法和过程误差法的目标函数,通过最大似然法可对上述r、k、e和q等参数进行求解,进而使用公式(6)和(7)求算相应的BMSY和MSY。
通过计算,当没有增殖放流时,MSY 约为12 t,对应的BMSY和EMSY分别约为和34 h。而当增殖放流存在时,MSY 的值也有所增加,即增殖放流群体提供了更多的产量(以图5 为例,年增殖放流苗种0.48 t 时,在BMSY和EMSY分别约等于71.1 t 和45 h 时,得到的MSY 约为12.7 t,)。因此,增殖放流对承受更大的捕捞强度以及获得更多的产量起到了积极的作用。
3.2 增殖放流量对模型的影响
当假定海域中初始资源生物量为80 t,且每年产量恒定在9 t 时,无增殖放流情况下的渔业资源生物量缓慢增加,最大值无法达到K的水平,而是趋于104 t左右。每年增殖放流苗种稳定在0.48 t 时(按照苗种平均体重2 g、成体平均体重100 g、有效增殖率0.245计算,将有5.88 t 的成体可供捕捞),生物量快速增加,并逐渐稳定在124 t 左右(图6a)。当增殖放流量从每年0.2 t 开始逐年增加时,虽然开始生物量的增长率不是最高,但生物量在持续地缓慢增加,并且随着放流数量不断加大,生物量逐渐逼近K(图6a)。若初始生物量不变,年产量增加到12 t 时,无增殖放流情况下到第20 年时,资源生物量将降至0。年增殖放流苗种稳定在0.48 t 的情况,生物量缓慢增加至94 t左右。而当增殖放流数量逐渐增加,在开始的几年里,由于放流量较小,无法弥补产量,而出现生物量下降的趋势,但随着增殖放流量的逐年增加,生物量开始攀升,并逐渐逼近K(图6b)。由此可见,不同增殖放流量和产量水平的组合,将直接影响海域中渔业资源生物量的水平,以及MSY 的大小。

图6 捕捞作用下不同增殖放流数量对渔业资源生物量的影响Fig.6 Effects of different stock enhancement numbers on fishery resource biomass under fishing
上述呈现的是将海域中原存群体与增殖群体结合在一起考虑的结果。可以想象,实施增殖放流后,增殖群体将对原存群体产生抑制作用。若将两者分开考虑,单独分析海域中原存群体,可以更加清晰地看到这种抑制作用。增殖剩余产量模型(公式(3))中,Bt表示第t年原存群体生物量(第t−1 年增殖放流群体中存活下来的个体与当年原存群体合并后,成为第t年的原存群体),而St表示第t年增殖放流苗种长到可捕成体规格时的生物量。图7 显示了年增殖放流量的变化对海域中原存群体所能提供产量的影响情况。当无增殖放流时,MSY 出现在K/2时,对应的EMSY约为34 h(图7)。而随着增殖放流量的增加,原存群体能提供的MSY 越来越小,并且对应的EMSY也逐渐降低(年增殖放流苗种为0.36 t、0.48 t 和0.60 t时,原存群体对应的MSY 和EMSY分别为10.1 t 和24 h、9.5 t 和21 h 以及9.2 t 和20 h)(图7)。原存群体出现MSY时对应的生物量仍旧是其对应的Ki/2(Ki代表不同年增殖放流数量情况下,原存群体所对应的环境容纳量,并且Ki<K)。由此可知,增殖放流导致原存群体的K变小,显示了增殖放流对原存群体的抑制作用。
3.3 增殖放流及捕捞策略对模型参数估算的影响

图7 不同增殖放流数量对海域中原存渔业资源产量−捕捞努力量的影响Fig.7 The effects of different stock enhancement numbers on the relationship between yield-fishing effort for the fishery resources that original existed in the sea area
本研究基于观测误差方法,使用增殖剩余产量模型对相关参数进行求解(详见公式(11))。不同增殖放流及捕捞策略下BMSY和MSY 的模拟估算结果如图8 所示(删除了部分异常估算值)。总体而言,随机增殖放流策略得到的BMSY和MSY 模拟估算结果变异性最小,且结果准确性最高,4 种捕捞过程得到的结果基本落在真实值区间内(图8d)。其他3 种放流策略情况下,BMSY和MSY 的评估结果分别有被低估和高估的趋势,但程度不一致(图8a 至图8c),其中产量持续增加的捕捞过程得到的模拟评估结果中值的误差最大,其余3 种捕捞过程模拟评估结果的中值与真实值较为接近。稳定和持续增加的增殖放流两种策略中,产量持续增加的捕捞策略对BMSY的评估结果均低于其他捕捞策略(图8a1和8b1),而MSY 的估算结果则均明显高于其他捕捞策略(图8a2 和8b2)。对于持续减少的增殖放流策略,当产量持续增加时,MSY 的估算结果虽然较其他捕捞策略更为离散,但中值差异不大(图8c2)。对比4 种增殖策略,持续增加的增殖放流得到了最小的BMSY中值估计值(图8b1)和最大MSY 中值估计值(图8b2)。
图9 展示了不同的生物量与放流量及捕捞努力量与放流量组合水平下的MSY 估计值。理论上,即使生物量等于0,当有增殖放流的持续补充时,也能维持低水平的MSY(图9a)。随着生物量增加,MSY水平也随之增加。当生物量在环境容纳量的30%~60%(图9a 中B在50~100 t)时,MSY 保持在较高水平。当生物量继续增加,MSY 开始下降。当生物量接近环境容纳量时,MSY 趋于0。随着捕捞努力量的增加,不同增殖放流量水平的MSY 均呈现先增高后下降的趋势(图9b)。在同一捕捞努力量水平下,增殖放流量增加时,MSY 先降低再升高,并且随着增殖放流量的持续增加而不断升高(图9b)。当增殖放流量逐渐增加,得到MSY 所对应的生物量和捕捞努力量变化不明显。

图8 不同增殖和捕捞策略下BMSY(左)和MSY(右)的模拟估算结果Fig.8 The simulation estimate results of BMSY(left) and MSY (right) under different stock enhancement and fishing strategies
4 讨论
4.1 增殖剩余产量模型增长率参数分析

图9 不同生物量和捕捞努力量与不同年增殖放流量水平组合下MSY 的模拟估算值Fig.9 The simulation estimates of MSY under combinations of different biomass and fishing effort levels with different stock enhancement levels
本研究在传统Schaefer 剩余产量模型基础上,将渔业资源生物量逻辑斯蒂增长特征以及增殖放流对生物量的影响相结合,提出了适用于定栖性种类的增殖剩余产量模型,并模拟不同的捕捞和增殖策略情况,对其MSY 等特征值进行了估算。该模型与传统Schaefer模型最大的不同就在于,增加了表示增殖效果的参数有效增殖率e。增殖剩余产量模型中,r与e两个参数均用于描述渔业资源生物量的增长率情况。虽然r和e所代表的原存群体和增殖群体最终的增长结果都通过Bt来体现,但当第t+1 年新的增殖发生之前,模型是将原存群体和增殖群体分开考虑。此外,值得注意的是,本研究在不同增殖和捕捞策略下模拟得到的参数r与e的相关系数平均值等于−0.68,相关性达到了统计学显著性水平(p<0.05)。由此可知,参数r和e两者之间存在显著的负相关,即原存群体和增殖群体两者的增长存在相互抑制作用,两个群体中一个增长加快必然导致另一个增长减慢。因此,在使用增殖剩余产量模型时,若能事先获得关于参数r和e的相关信息,或者固定其中1 个参数值,将有助于获得准确的参数估算结果。
增殖剩余产量模型对参数r和e的表达以及原存群体和增殖群体两者的相互抑制性,关系到如何对两个群体开展分析的问题,即是将两个群体综合在一起考虑,还是将两者分别考虑。增殖剩余产量模型的最终结果是将两个群体综合在一起呈现的。图6 表明,增殖群体确实能够使产量持续并维持在较高的水平,特别是当产量过高,生物量开始下降时,此时增加放流量能够对因捕捞而降低的生物量起到补偿作用。然而,如果将两个群体分开考虑,则能够清晰看到两者之间相互抑制的效应。如图7 所示,随着每年增殖量的增加,原存群体所维持的MSY 水平逐渐降低,并且EMSY也随之减小,说明增殖放流实施后,原存群体提供产量的作用被逐渐弱化。以无增殖放流和每年增殖放流0.48 t 苗种两种情况为例,当没有增殖时,原存群体的MSY=11.91 t,相应的BMSY=84.13 t。而当每年增殖放流0.48 t 苗种以后,总的MSY=12.72 t,此时原存群体的BMSY=71.14 t。假如在无增殖放流时,把生物量维持在71.14 t(即年放流0.48 t 时原存群体的BMSY)的水平上,此时MSY=9.51 t,说明增殖群体弥补了3.21 t 的产量。而这3.21 t 的产量来自增殖群体和原存群体两方面,即增殖苗种生长至可供捕捞尺寸时的群体以及从84.13 t 降到71.14 t 后减少的12.99 t的原存群体,这两部分加在一起提供了比无增殖时的MSY 多出来的3.21 t。
4.2 增殖放流与捕捞策略对模型的影响
在增殖放流作用影响下,通常高产量情况下评估得到的MSY 值要高于其他情况,特别是增殖放流量持续增加的时候(图8)。这主要受到模型求解参数结果的影响。增殖剩余产量模型对参数r和e的求算均有不同程度偏高的趋势,其中,参数e的偏高程度略大于r。当增殖放流量持续增加时,生物量不断增长,因此参数r和e高估趋势增加,导致MSY 值变大(见公式(7))。又由于e的高估程度大于r,因此BMSY值相对变小(见公式(6))。对于产量逐年增加的情况,当增殖放流量也持续增加时,此时体现生物量的变化率较大,因此参数r和e的估计值较大,MSY也较大;而当增殖放流量持续减少时,生物量的变化率减小,则参数r和e估计偏高程度降低,MSY 也相应减小(图8b,图8c)。随机增殖放流和产量先增后降的策略得到的BMSY和MSY 模拟估算结果变异性最小(图8),说明同类数据的对比性有利于模型评估得到稳定的结果。对比图8b 和8c 可发现,当增殖放流与产量变化趋势一致时,得到MSY 的评估结果变异性较小,而相反时则较大。说明非同类数据变化相一致时,有助于提高模型参数估算的稳定性。
从资源整体来看,实施增殖放流量的大小对MSY水平的影响并不明显(图9a),表明增殖剩余产量模型中eS所表示的增殖放流群体可补充到资源群体并被捕捞利用的数量基本是稳定的,即S增大则e将减小。少量的增殖放流,效果反而不如无增殖放流(图9b),显示了此时增殖放流对原存群体的抑制作用大于促进作用。当增殖放流量逐渐增加时,促进作用开始显现,此时生物量的变化受增殖放流作用的影响越来越显著。
4.3 研究的不足与展望
本研究中对参数的估算使用了观测误差法,实践证明观测误差法具有一定的优越性[9−10]。然而,误差的来源形式是多种多样的,不仅包括过程误差和观测误差,还存在许多其他形式的误差类型[11]。传统剩余产量模型中的参数(r、K和q)之间存在着高度的相关性[12],本研究提出的增殖剩余产量模型,参数之间同样存在相关性。事实上,在许多渔业资源评估的模型中都存在参数相关的情况,这难免对参数估算结果产生影响,但影响程度有多大,则需进一步的分析与探讨。此外,增殖剩余产量模型中相应变量,如B、S和C之间也会产生相互影响,特别是每年的增殖放流量发生较大变化的时候,通过公式(5)得到的BMSY求算结果将会存在误差。因此,公式(6)的结果应以每年的增殖放流量稳定为前提,或者使用数值模拟的方式估算MSY,以避免多变量之间复杂的关系。
为了进一步丰富剩余产量模型的应用,许多学者在传统模型基础上演变出了系列模型[13-16]。而在渔业资源评估工作不断发展过程中,模型的发展也是内在的需求。本研究提出了一个适用于增殖放流背景下的定栖性种类剩余产量模型。选择定栖性种类,主要是考虑其移动性较弱,当增殖放流实施后,不会出现栖息海域范围发生变化,从而引起环境容纳量改变的情况,这样就使模型参数不至于过于复杂。受此条件的限制,该模型比较适用于海洋牧场内增殖的定栖性种类,或者那些在比较清晰的作业边界内,且不会超出边界范围的增殖目标种。在今后的研究中,我们将针对这一点对模型作进一步的调整,使其适用范围更加广泛。与传统剩余产量模型相似,增殖剩余产量模型对参数的评估结果容易受到参数所设置初始值的影响,在后续的研究中,我们将考虑开展敏感性评估和根据实际观测进行验证。此外,模型中新增加的参数e会受到其他因素的影响,比如环境因子、人工鱼礁集鱼效果等等,这些在本研究中未进行细化,因此也同样将是我们未来研究的重点内容。
