改进的SEREP缩聚法在航天器结构动力学模型修正中的应用

李建宏宇，庞贺伟

（1.北京卫星环境工程研究所；2.可靠性与环境工程技术重点实验室；3.中国空间技术研究院：北京100094）

0 引言

由于实际条件的限制，无法在地面完全模拟航天器在整个寿命周期内全部的动力学载荷，需要借助有限元模型进行动力学仿真分析，因此航天器结构有限元模型的动力学验证是一项重要工作。这项工作要求结构的动力学模型要准确反映结构的动力学特性，而使用实测数据对有限元模型进行修正是获得高精度有限元模型的有效手段。基于频率响应的模型修正方法在航天器结构模型修正中具有重要的研究价值，因为该方法无须对模态参数进行辨识，可避免引入新的误差，而且可以充分利用动力学试验产生的大量实测数据。航天器结构有限元模型的自由度数会达到十万甚至百万量级，而动力学试验传感器测量的自由度数最多能达到几百个，远小于有限元模型的自由度数。因此，需要首先将有限元模型进行模型缩聚，再进行模型修正；而如果模型缩聚方法存在较大误差，会导致模型修正工作失去意义。

在以往对航天器结构的动力学研究中，主要目的是确保结构在动力学载荷下不发生失效或破坏，关注的频段一般低于100 Hz。随着应用需求的不断扩展和性能指标的不断提高，微振动对有效载荷性能的影响逐渐凸显。航天器在轨微振动的扰动力和扰动力矩以中高频率的谐波为主，为了对微振动进行有效的仿真计算，需要对有限元模型进行基于中高频段频率响应的模型修正。而常用的Guyan、IRS、IIRS、SEREP等方法的中高频段频率响应计算存在误差，会导致模型修正结果错误。

本文试图建立适用于航天器结构的改进的SEREP缩聚方法，旨在保证缩聚模型能准确反映结构在中高频段的动力学特性。

1 模型缩聚方法

有限元模型的无阻尼动力学方程在频域内可以表示为

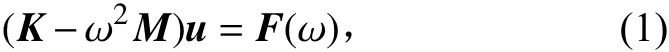
式中：K 为刚度矩阵；ω为角频率；M 为质量矩阵；u为位移的频率响应矢量；F(ω)为力载荷矢量。

将动力学方程根据主自由度和从自由度进行分块，其中主自由度包括载荷施加的自由度、边界条件约束的自由度和传感器测量的自由度，可以得到

式中：TKT 为缩聚后的刚度矩阵；TMT 为缩聚后的质量矩阵。

1.1 Guyan缩聚法

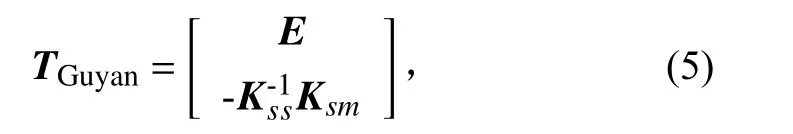
Guyan 缩聚法是由Guyan 和Irons提出的，属于静力学缩聚。其转换矩阵为其中E 为单位矩阵。忽略式(2)中第2行的惯性项可得到由于忽略了惯性项，Guyan 缩聚法的动力学特性误差将随着频率的增高而增大。

1.2 IRS缩聚法与IIRS缩聚法

O’Callahan 对Guyan 缩聚法进行改进，提出了IRS缩聚方法，其转换矩阵为

迭代初始化为Guyan 缩聚法，首次迭代为IRS缩聚法，即

IRS法和IIRS法的精度相比Guyan 法均有所提高，其中IIRS随着迭代的进行是收敛的，文献[10]证明了IIRS法收敛于m=r 的SEREP缩聚法。

1.3 SEREP缩聚法

SEREP缩聚法基于模态分析的结果，故需首先对有限元模型进行模态分析，求解其前r 阶特征值λ及特征向量Φ。

特征值问题为

根据主自由度和从自由度对特征向量进行分块得到

SEREP缩聚法基于结构的模态分析结果，其精度得到大幅提高，已经得到众多学者的关注，并成功应用到航天器结构的模型缩聚和传感器布局优化等问题中。

1.4 模型缩聚的误差分析

模型缩聚的误差来源主要有2个：

1）模型缩聚方法在推导时引入近似计算或者忽略某些因素而引起的误差，如：Guyan 推导过程中忽略惯性项，IRS方法和IIRS方法中引入Guyan缩聚法，SEREP 缩聚法中引入广义逆等。

2）缩聚后的模型阶数与主自由度数是相同的，而主自由度的个数受现实试验条件约束。对于需要考虑中高频段动力学特性的复杂结构，其特征值比较密集，导致在需要考虑频段内的特征值的个数远多于主自由度的个数。而由于阶数过低，缩聚后的模型对应的线性子空间不足以全面反映原模型的动力学特性。

2 改进的SEREP 缩聚法

为了满足缩聚模型在中高频段的精度要求，根据1.4节对模型缩聚误差来源的分析，本文提出了改进的SEREP缩聚法。在SEREP缩聚法中，当m=r 时，SEREP缩聚法与考虑前r 阶模态的模态叠加法的线性子空间是相同的。模态叠加法已被广泛应用于实际工程中，其准确性已得到验证。对于考虑中高频段的复杂结构模型缩聚问题，试验测量的自由度数往往小于r，为了使m=r，可以拓展主自由度的个数，引入无实际物理意义的(r-m)维度得到扩展主自由度u˜ 以满足关系

同时，需要满足T 的每一列组成的线性子空间与前r 阶特征向量Φ的每一列组成的线性子空间是相同的。本文给出一种构造方式，对Φ 进行2步列变换得到满足式(15)形式的T：

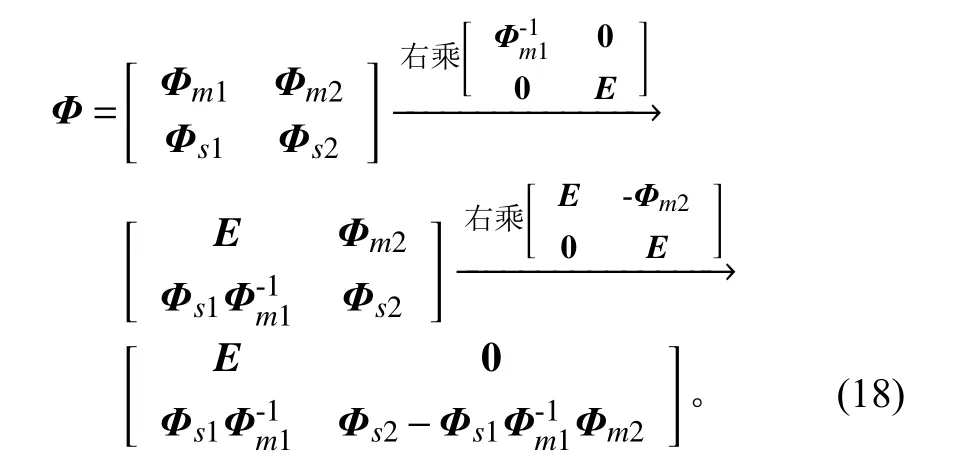
将列变换过程写为矩阵相乘的形式，有

在计算缩聚后的刚度矩阵和质量矩阵时，使用Nastran 进行模态分析只需要输出特征值和特征向量在主自由度分量的值，不需要输出全部的特征向量信息，以及刚度矩阵和质量矩阵信息。

3 数值算例

以某航天器中的控制力矩陀螺隔振平台作为算例。控制力矩陀螺隔振平台由6个控制力矩陀螺及其外壳、支撑刚架，以及5 个隔振器和5个底座构成。其中：5个控制力矩陀螺及其外壳固定在支撑钢架上；1个控制力矩陀螺及其外壳固定在与支撑钢架相连的底座上，位于结构的中心。控制力矩陀螺及其外壳使用集中质量单元建模；支撑刚架使用梁单元建模；隔振器使用pbush 单元建模。有限元模型中还有板单元、3D单元的MPC等。整个有限元模型由29 000+个节点、28 000个单元组成。选取结构上59个节点（包括6个控制力矩陀螺的质心、5个底座的固支点、5个隔振器端点以及48个刚架连接节点）的x、y、z 平动方向上的自由度（共计177个自由度）作为主自由度，如图1所示。

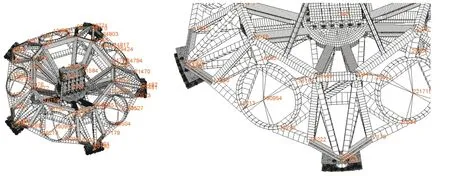
图1 控制力矩陀螺隔振平台有限元模型Fig.1 Finite element model of the control torque gyroscope isolation platform

航天器在轨运行时，控制力矩陀螺会产生一系列与转速相关的谐波扰动，是航天器微振动主要的扰动源之一。通过试验测量，控制力矩陀螺产生扰动的峰值在123 Hz 及其倍频上。根据高精度的遥感需求，需要保证控制力矩陀螺隔振平台的动力学模型能在0～300 Hz 频段准确反映实际结构的频率响应。使用模态叠加法进行频率响应分析时，Nastran 的用户手册中建议至少计算频段内所有的模态；为了得到更精确的计算结果，则要计算该频段最高频率的2倍或3倍频率内的所有模态。本文将计算频率低于900 Hz 的全部模态（共758阶），并作为衡量模型缩聚方法准确性的基准。分别对缩聚后的模型进行模态分析和频率响应分析，以确认缩聚后模型的动力学特性。

3.1 模态频率计算结果误差比较

使用模型缩聚方法对有限元模型进行缩聚，设转换矩阵为T。缩聚后的特征值问题为

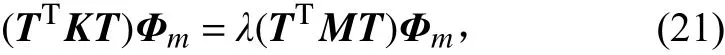
特征值λ与模态频率f 的关系为

分别使用Guyan 缩聚法、IRS缩聚法、IIRS缩聚法、SEREP缩聚法和改进的SEREP缩聚法进行模型缩聚。其中：IIRS缩聚法迭代10次；SEREP缩聚法分为3种情况，分别为m=r+10=177，m=r=177，m=r-10=177；改进的SEREP缩聚法考虑前758阶模态，即r=758。使用Nastran 对模型前758阶模态进行计算分析，得到的模态频率作为误差分析基准。

模型的主自由度为177个，Guyan 缩聚法、IRS缩聚法、IIRS缩聚法和SEREP缩聚法缩聚后的模型的特征值共有177个，与缩聚前模型的前177阶模态特征值进行对比；改进的SEREP缩聚法缩聚后的模型的特征值有758个，与缩聚前模型的全部特征值进行对比。

模型缩聚后，模态频率前32阶（低于100 Hz）的相对误差见表1。

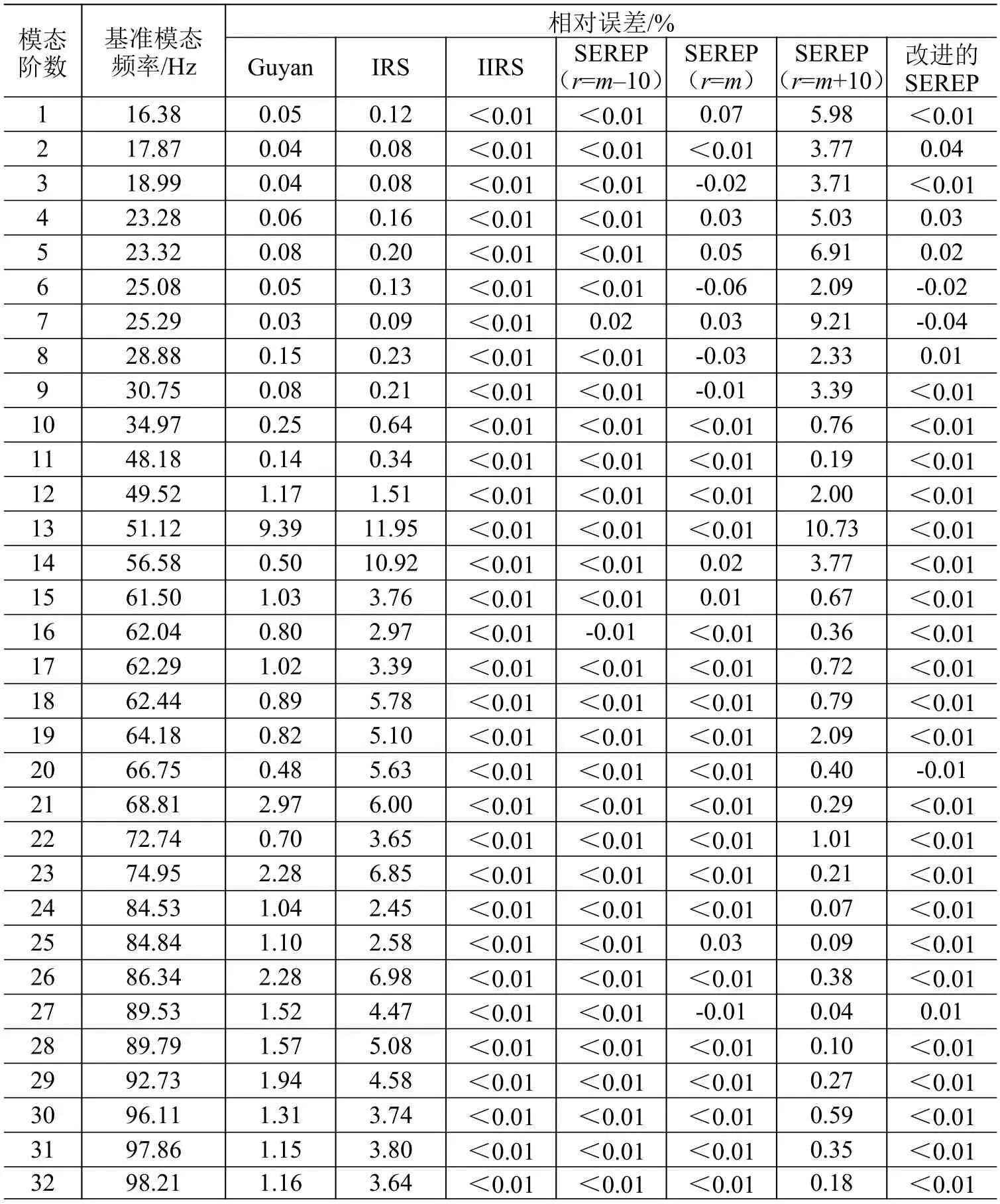
表1 模型缩聚后模态频率前32阶的相对误差Table1 Relativeerrorsof modal frequency of the reduced model for the first 32 orders

ECSS-E-ST-32-11C标准对缩聚模型的误差提出了要求：对于主模态，缩聚后模型的模态频率相对误差应控制在3%以内；对于其他模态（小于100 Hz），模态频率的相对误差可以放宽到5%。如果模态频率的相对误差大于100%，则说明缩聚后模型的特征值已经完全失真。

从表1可以看出，对于模态频率低于100 Hz的模态，几种模型缩聚方法的精度都比较高，其中：IIRS缩聚法、SEREP缩聚法（r=m-10）、SEREP缩聚法（r=m）和改进的SEREP 缩聚法完全满足实际工程应用的要求；Guyan 缩聚法仅在第13阶模态的相对误差较大（9.39%）；IRS缩聚法和SEREP缩聚法（r=m+10）的误差相对较大，但亦控制在15%内，未出现完全失真的情况。模型缩聚后，模态频率33阶～178阶的相对误差见图2。

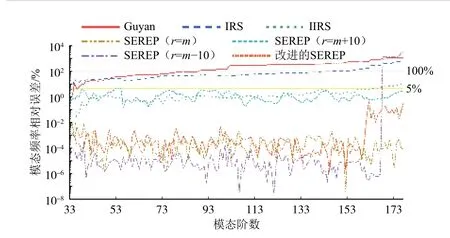
图2 模型缩聚后模态频率33阶～178阶的相对误差Fig.2 Relative errors of modal frequency of the reduced model from the 33rd order to the 178th order

从图2可以看出：当模态频率高于100 Hz时，Guyana 缩聚法和IRS缩聚法计算出的模态频率的相对误差快速扩大并完全失真。IIRS缩聚法的精度相对于前两者得到了提高，并没有出现失真的情况，但最大相对误差也超过了10%。SEREP缩聚法的精度进一步提高，当r=m+10时相对误差较大，与IIRS缩聚法相当，但最大相对误差没有超过10%；当r=m时模态频率相对误差极低；当r=m-10时，前167阶模态的模态频率相对误差极低，后10阶模态频率则完全失真。这是由于引入了广义逆，生成缩聚后线性子空间的向量组的秩为167，在该线性子空间内最大的10 个广义特征值实际为正无穷。

管理是门复杂的学科。管理既是科学，也是艺术，专业化、系统化学习是必须的。“管院在线”将深厚的线下培训行业专长与丰富的集团远程培训经验相结合，通过专业化、体系化和权威性的运营方案和云平台，使客户了解更多培训模式，开展更丰富、更优质的业务。

使用改进的SEREP法缩聚后，模型的模态频率相对误差直方图见图3。由图可知，改进的SEREP缩聚法计算出的模态频率相对误差绝大多数都低于0.5%，最高不超过2.5%。可见，通过改进的SEREP缩聚法缩聚后的模型可以准确反映原模型前758阶（低于900 Hz）的模态频率。

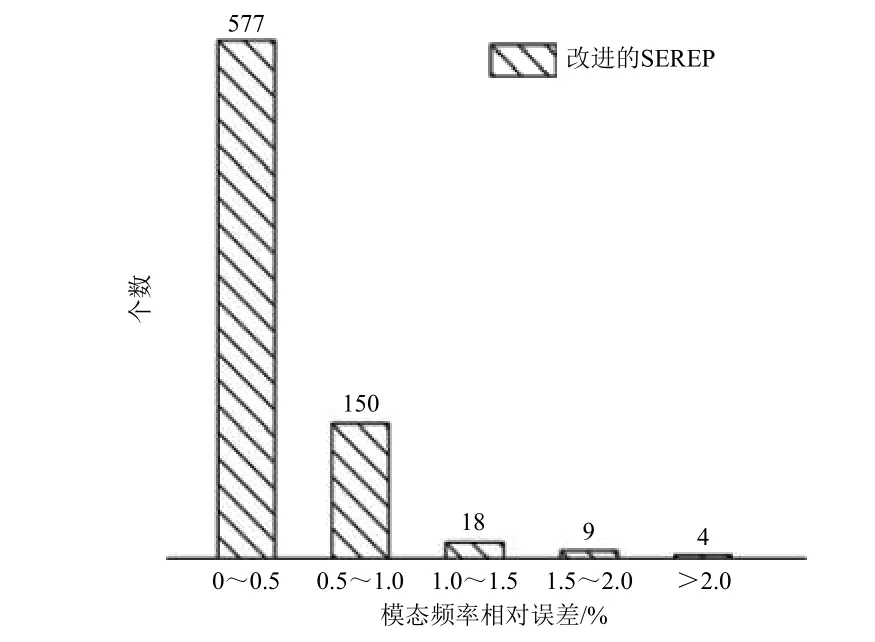
图3 使用改进的SEREP 缩聚后模型满足相对误差限的模态频率个数Fig.3 The number of modal frequencieswithin a certain error range,using improved SEREP reduction

3.2 频率响应计算结果误差比较

针对控制力矩陀螺隔振平台的载荷，即控制力矩陀螺质心上的扰动力，计算0～300 Hz 的结构位移频率响应。比较采用不同缩聚方法计算的隔振器端点的z 方向平动位移频率响应和中心控制力矩陀螺质心的z 方向平动位移频率响应。对于Guyan缩聚法、IRS缩聚法、IIRS缩聚法和SEREP缩聚法，主自由度的位移频率响应的计算公式为

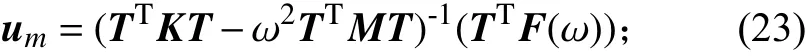
对于改进的SEREP缩聚法，主自由度的位移频率响应的计算公式为

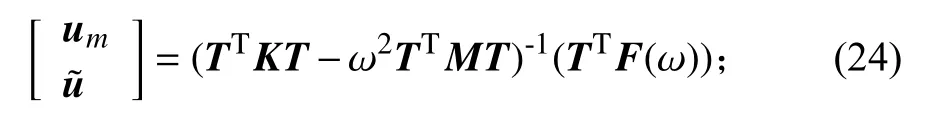
使用直接法计算位移频率响应，作为结果比较的基准。直接法计算位移频率响应的公式为

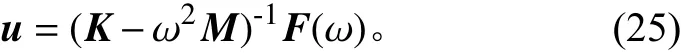
将整个频段分为4个频段：0～50 Hz，50～100 Hz，100～250 Hz 和250～300 Hz。比较采用不同缩聚方法分别在不同频段计算的频率响应的误差，结果如图4～图7所示。

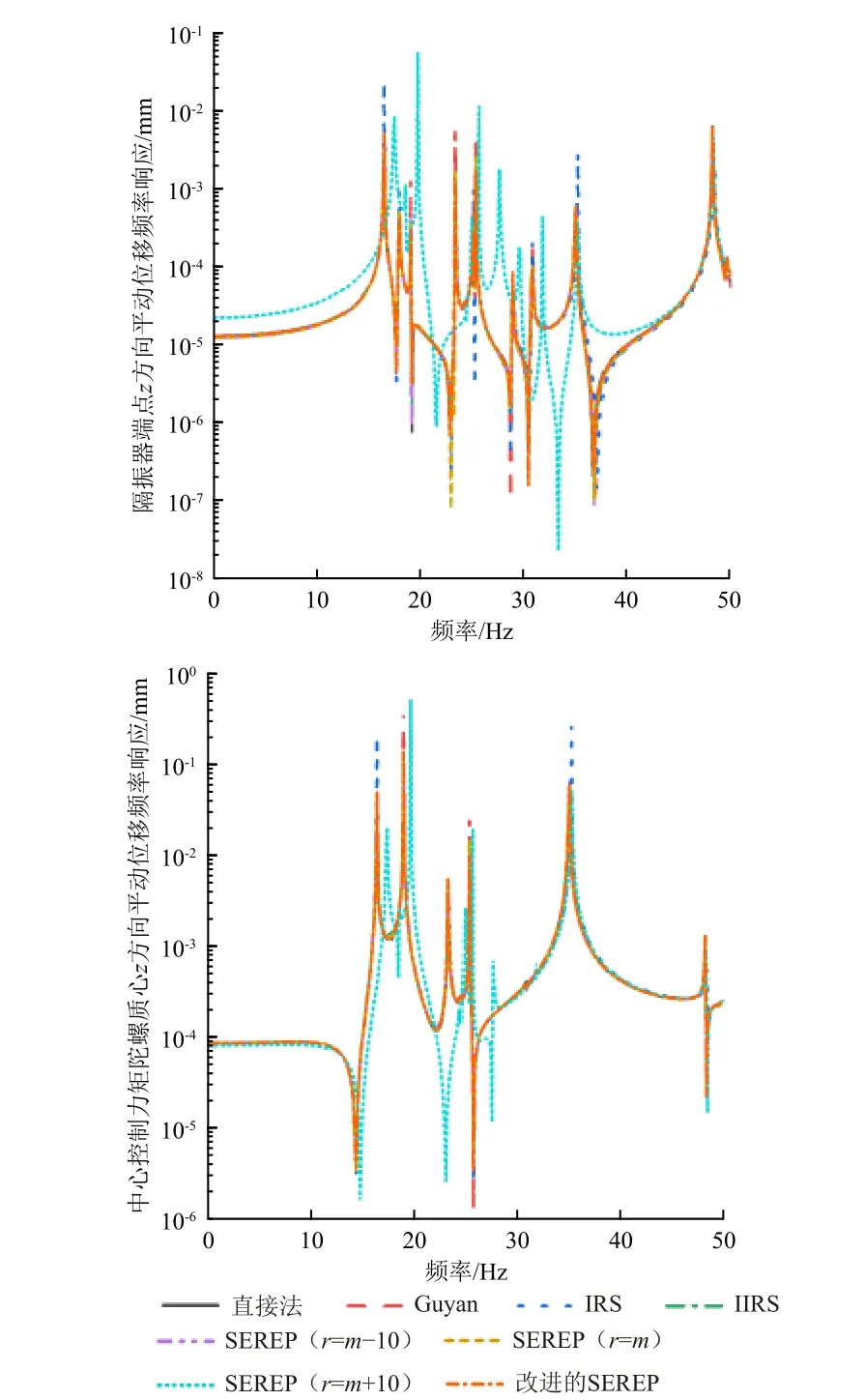
图4 缩聚模型在0～50 Hz 频段计算的频率响应Fig.4 Frequency response of the reduced models for frequency between 0 Hz and 50 Hz

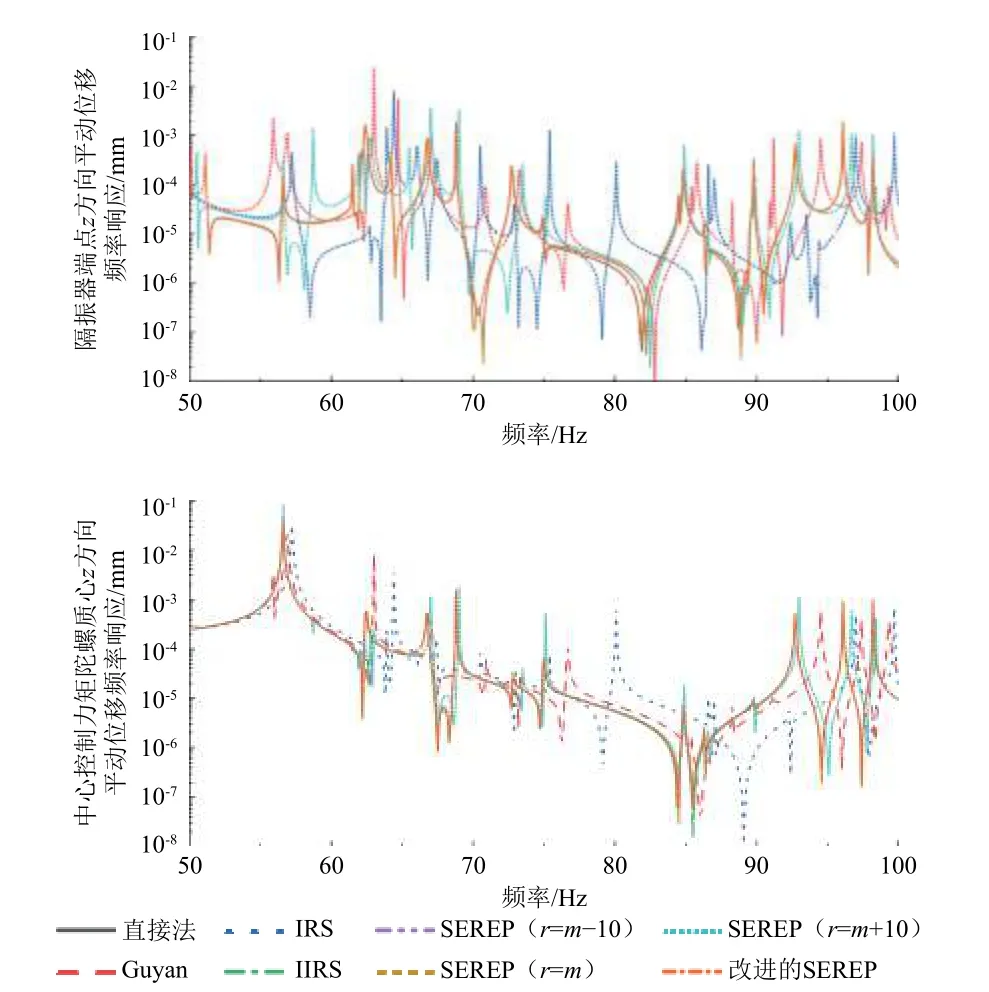
图5 缩聚模型在50～100 Hz 频段计算的频率响应Fig.5 Frequency response of reduced models for frequency between 50 Hz and 100 Hz

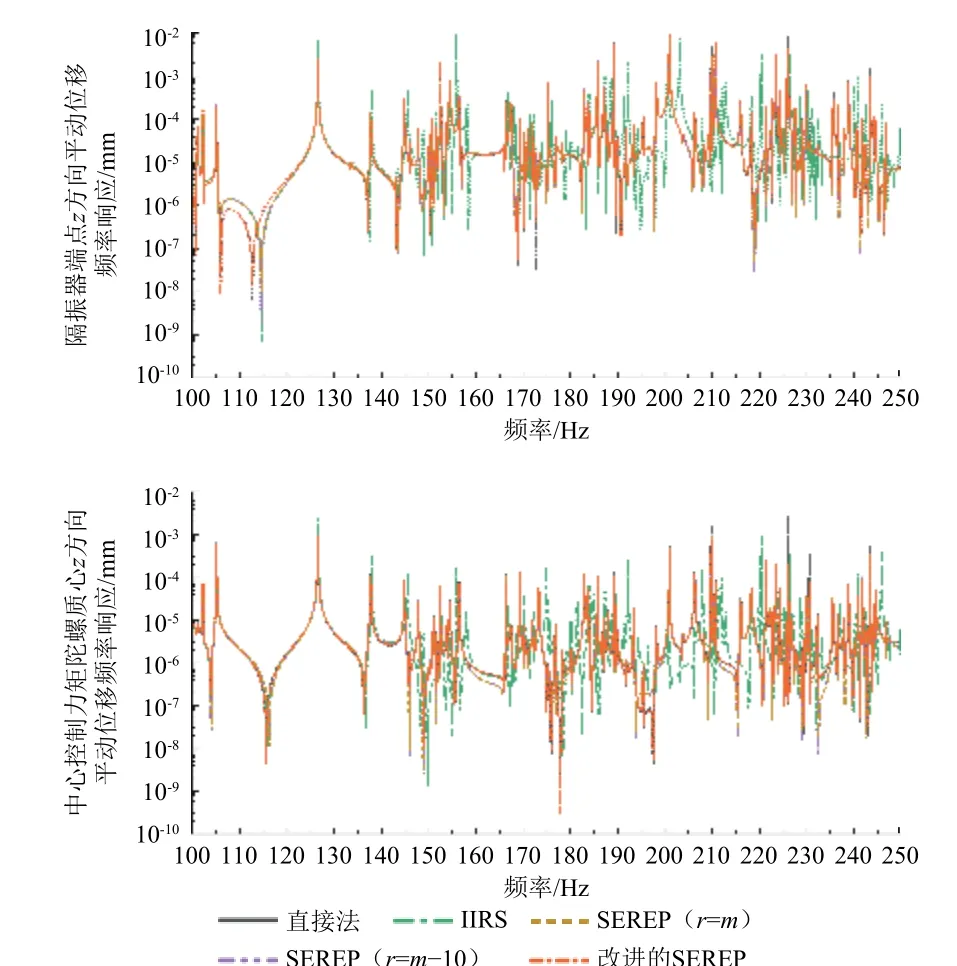
图6 缩聚模型在100～250 Hz 频段计算的频率响应Fig.6 Frequency response of reduced models for frequency between 100 Hz and 250 Hz

从图4可以看出，在0～50 Hz 频段，Guyan 缩聚法、IRS缩聚法、IIRS缩聚法、SEREP缩聚法（r=m-10）、SEREP缩聚法（r=m）和改进的SEREP缩聚法的误差较小，频率响应曲线几乎与基准曲线重合。这是由于上述几种模型缩聚方法对于模态频率低于100 Hz 的模态的计算精度较高。而对于SEREP缩聚法（r=m+10），由于其在低于50 Hz 的模态计算中存在较大误差，导致其在0～50 Hz 频段的频率响应计算结果误差较大。

从图6可以看出，在100～250 Hz 频段，SEREP缩聚法（r=m-10）、SEREP缩聚法（r=m）和改进的SEREP缩聚法缩聚后的模型的频率响应与基准相比误差较小，而IIRS缩聚方法出现较大误差。这是由于IIRS在100 Hz 以上模态频率分析的相对误差逐渐增大，最大值已经超过了10%。

综上，在0～250 Hz 频段，缩聚模型的频率响应误差与缩聚模型的模态分析误差紧密相关。这部分误差源自模型缩聚方法在推导时引入近似计算或者忽略某些因素引入的系统误差。

图7 缩聚模型在250～300 Hz 频段计算的频率响应Fig.7 Frequency response of reduced models for frequency between 250 Hz and 300 Hz

从图7可以看出，在250～300 Hz 频段，SEREP缩聚法（r=m-10）和SEREP缩聚法（r=m）缩聚后的模型的频率响应与基准相比缺少大量波峰与波谷，这是由于缩聚模型没有模态频率大于270 Hz 的模态，这部分误差是由于缩聚后的模型阶数过低引起的。

由于改进的SEREP缩聚法可以准确反映模型低于900 Hz 的全部模态频率，使得该方法在0～300 Hz 整个频域内计算的频率响应均与基准几乎重合，说明使用该方法进行缩聚后的模型能够准确反映结构在0～300 Hz 频域内的动力学特性。

4 结束语

针对现有的模型缩聚方法无法准确反映复杂结构在中高频段动力学特性的问题，本文提出了改进的SEREP模型缩聚方法。该方法构造的线性子空间与模态特征向量所构成的线性子空间相同；为了解决缩聚模型主自由度数受限于试验条件而数量不足的问题，引入了扩展主自由度，其可以根据频域的大小和实际计算精度的需求调整缩聚后模型的维数，适用于存在密集模态频率的复杂结构的模型缩聚。本文以实际航天器结构的算例证明，使用改进的SEREP模型缩聚方法进行缩聚后的模型可以准确反映结构在全频域的动力学特性。

本文为接下来研究基于中高频段频率响应的模型修正问题提供了必要的方法与手段。