基于Toeplitz矩阵重构的无人机相干信号DOA估计算法

曹聪慧 兰强 侯群

（1.江汉大学人工智能学院；人工智能研究院，湖北 武汉 430056；2.东风汽车财务有限公司，湖北 武汉 430056）

1 引言

近年来，无人机(UAV)等低空目标急剧增加，UAV的成本逐渐降低，开发厂家增多，规模加大[1]。2016年艾瑞咨询的报告预测到2025年国内民用UAV有可能会形成750亿人民币的规模[2]。无人机在军事作战、航空摄影和录像、测绘、搜索救援、环境监测和精准农业等军事和民用相关产业中都有巨大的应用前景[3]。除了良性用途之外，UAV造成的危害和安全隐患也已经逐渐引起了公众的关注。对无人机的失控和漏检可能会对军事作战、空中交通、人类生活和隐私构成严重的威胁[4-6]。而无人机射频检测是被动接收UAV本身发出的射频信号，通过特征提取和信号分析，来对UAV进行检测和DOA估计。

目前，对于目标检测和DOA估计的研究较多。S.Jardak提出了一种新的多目标射频检测方法，将天线阵列划分为多个重叠集合，每个集合由四个天线组成，并提出两种算法来组合多组输出提高检测性能，该算法能够定位两个目标，并且二维角度估计都保持有较低的误差[7]。Y.Fu等对调频立体声信号的结构和模糊函数进行了详细分析，阐述了侧峰被动识别方法，该方法可以消除假目标并被动检测出真实目标[8]。文献[9]利用从基站和客户端设备发出的所有有用射频信号实现被动相干定位。H.Y.Zhao设计了用于多基站雷达射频检测的线性融合框架[10]。通过采用基于修正偏转系数的优化算法，确定了最佳加权系数，并对全局检测器进行了估计，得到了全局检测器的近似表达式。文献[11]基于广义贝叶斯风险开发了多检测系统，该系统可用于联合识别和估计目标。文献[12]利用DVB-T机会发射机，解决了多径情景下的移动目标射频检测问题。Zaimbashi等人提出的一致最强大不变量测器来检测机动目标射频信号[13]。文献[14]提出了一种球-时空-状态空间稀疏大孔径阵列模型，它结合了目标范围、方向和多普勒效应以及阵列几何结构与扩展卡尔曼滤波器一起被集成，可同时检测多个射频信号。

综上，现有的射频检测算法主要侧重于机会辐射源射频信号的检测和参数估计，而针对能自身辐射信号的UAV射频检测算法还相对较少。本文设计了基于Toeplitz矩阵重构的无人机相干信号DOA估计算法，能够对UAV进行方向估计，准确率较高。

2 阵列模型设计

若考虑有N个UAV射频信号入射到如均匀圆阵模型中，阵元数为M，以圆心为参考点，前L个UAV信号相干，后N-L个UAV信号非相干。其中，第m个阵元收到的信号可表示为：

其中，si(t)是第i个UAV的复包络，r是圆阵的半径，r选择UAV信号跳频频段2.4 GHz-2.5 GHz的中心频率2.45 GHz对应波长的一半，λi是第i个UAV信号中心频率对应的波 长，nm(t)为AWGN，其 方 差 是σ2，均 值 为0，βi，i=1,2,…,L为衰落系数。均匀圆阵收到的UAV信号矢量形式如下式表示：

其中，阵列流型可表示为：

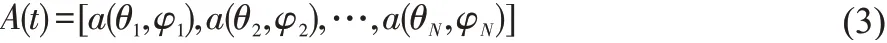
其中，方向矢量a(θi,φi)可表示为：

上式不符合范德蒙德结构。普通的均匀圆阵很难直接用于UAV信号的解相干，需要将较复杂的均匀圆阵使用模式激励算法转换为虚拟均匀线阵，构建符合范德蒙德结构的阵列流型，从而实现UAV信号的解相干。利用变换矩阵T对式(2)进行变换可以表示为：

其中，变换矩阵T可以表示为：

而

其中，Jk(β)是km阶第一类贝塞尔函数是模式激励算法中的最大模式数。在满足2h+1≤M条件下，经过变换以后虚拟线阵流型矩阵如式(9)所示。

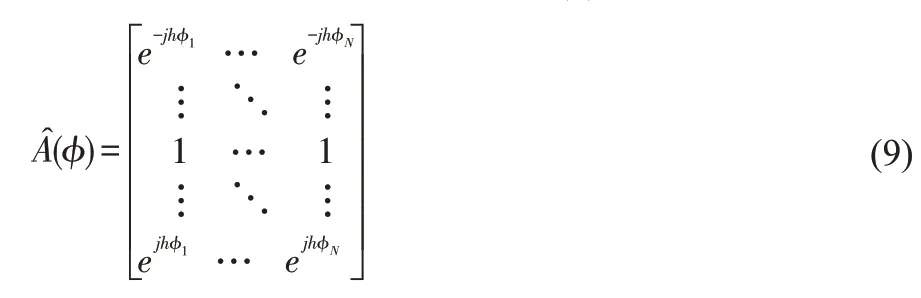
由此，上式符合范德蒙德的结构形式，可使用该形式的阵列流型进一步对UAV信号进行解相干和DOA估计。经矩阵变换后的虚拟线阵是K=2h+1个阵元组成的，阵元间距为d。

3 基于Toeplitz矩阵重构的无人机相干信号DOA估计

由上节转换后的阵列模型可看出，当参考阵元是中间阵元时，虚拟线阵收到的信号如式(10)所示：

协方差矩阵可以表示为

其中，第km行、第kn列的元素可以表示为：

其中，

其中，是噪声协方差，且：

为了对无人机信号解相干，需要重构矩阵。故利用协方差矩阵第m行元素构建Toeplitz矩阵Rp(ϕ)，如式(17)所示：

可知，Rp(ϕ)是(h+1)×(h+1)维矩阵，式(17)中Ar满足范德蒙德结构，该矩阵包含各个UAV信号的信息，若ϕi≠ϕj，则矩阵中各列互不相关，故rank(Ar)=N。而D(km)=diag(d1,d2,…,dN)，若 对角 阵 元素 都 不 为0，则 可 知rank(D(km))=N，因此可对UAV信号进行解相干。同时也用第kn列元素构建Toeplitz矩阵Rq(ϕ)，可以表示为：

同样，上式中的A͂r也符合范德蒙德结构形式，该矩阵也包含各个UAV信号的信息，A͂r和D(kn)的秩也为N。为了更精确地估计DOA，这里根据Toeplitz矩阵的性质，对上述协方差矩阵做一定变形，使用整个协方差矩阵对UAV方向做估计，如下式所示：

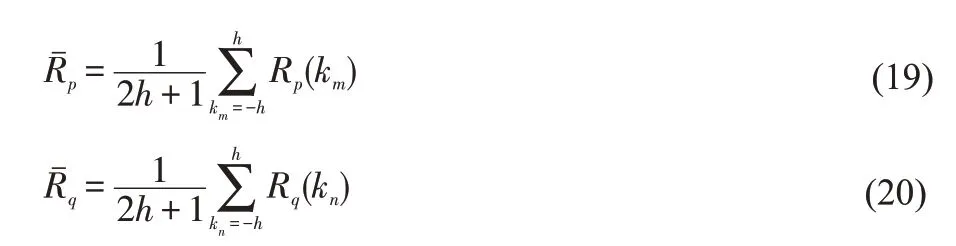
设计了一种新协方差矩阵形式，如下式所示：

可看出，该算法在对角矩阵秩不变的基础上，做了整体平滑，既能对UAV信号解相干，又能减轻噪声影响，从而能有效增加DOA估计精度。接下来通过对解相干后的协方差矩阵做特征分解，解算出其两种子空间矩阵，然后利用子空间算法来对UAV信号进行高分辨率的二维DOA估计。

4 性能仿真

假设空间内有3个入射的UAV信号，其中信号1和信号2为具有相同中心频率的相干信号，其中心频率都为2.42 GHz，波 达 方 向 角ϕ1和ϕ2分 别 为(θ1,φ1)=(81°,149°)和(θ2,φ2)=(84°,152°)。而信号3为独立于信号1和信号2的信号，其的中心频率为2.46 GHz，俯仰与方位角是83°与30°快拍数是1000，SNR是5dB。7阵元数虚拟线阵在进行完Toeplitz矩阵重构与特征分解之后的空间谱如图1所示，其中，方位角采样间隔是0.5°，其的采样范围是0°～360°，俯仰角采样间隔是0.5°，其采样范围是45°～90°。

可看出，该算法可实现对相干UAV信号的二维DOA估计，估计出的三个UAV信号的俯仰角为80.4 °、84.5 °和83.2 °，方位角分别为150.1 °、152.4 °和30.3 °，此次实验的UAV信号二维DOA估计误差小于等于1.1 °。图2为不同信噪比下，两种算法的均方根误差，可见，均方根误差随着信噪比的增加而逐渐降低，并且，提出的算法的性能要优于FBSS算法。

图2 两种算法的精度性能

5 结语

本文建立了7阵元数虚拟线阵模型，无人机相干信号作为入射的射频信号，据无人机信号的特点，通过对协方差矩阵进行Toeplitz矩阵重构，提出了基于Toeplitz矩阵重构的无人机相干信号DOA估计算法，并实现了对无人机信号的二维DOA估计，最后仿真并分析了该算法的性能。仿真分析表明本文方法的DOA估计准确率较高，性能较好。