轧机自动厚度混沌系统ADRC控制器设计

梁卫征，曹志新，张瑞成

（华北理工大学电气工程学院，唐山 063210）

0 引言

在带钢轧制过程中，自动厚度控制（AGC）在板带材质量控制中应用非常普遍。连轧AGC 系统具有非线性、大滞后等特性，支撑辊偏心符合正弦规律，文献［1］综合考虑摩擦、轧辊偏心等因素建立了轧机厚度混沌系统模型，并对其混沌特性进行了分析。文献［2］也论证了板带厚度控制系统产生混沌的条件。这种混沌现象的出现将严重影响轧制产品的精度。因此，针对连轧AGC 系统，设计一种具有较强鲁棒性的轧机AGC 混沌控制系统具有重要的现实工程价值。

自抗扰控制因其结构简单且不依赖被控对象的精确数学模型等特点，应用十分广泛。目前在机器人、电力系统、电机调速等领域出现了一系列的研究成果［3-7］。因此，针对板带轧机AGC 系统存在的混沌问题，使用ADRC 方法设计了一种轧机AGC 系统控制器，并进行了实验仿真，控制效果良好。

1 轧机自动厚度混沌系统模型的建立

在轧制过程中，设板带材的厚度变化为x，如图1 所示。在轧制过程中，轧制压力导致板带材厚度变化而产生的恢复力符合弹跳方程，但材料恢复力不符合胡克定律，属于物理非线性变化。文献［1］建立了如式（1）所示的轧机AGC 系统的非线性参激振动模型：

图1 轧辊偏心示意图

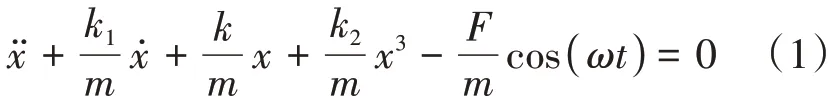
式中x为轧辊偏心位移，k1为阻尼系数，k、k2为弹性变形系数，F、ω分别为轧辊偏心力的幅值和角频率，m为轧辊的质量。

假设τ=ω0t，其中ω0=，并且令：=从而可将式（1）整理为：

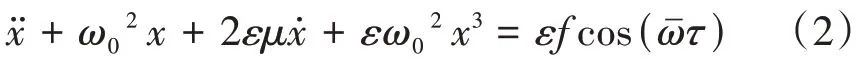
当ω0=0.02，ε=0.02，μ=0.01，f=0.03，变化时对应的系统分岔图和最大Lyapunov 指数图如图2 所示。当大于0.60199 后，最大Lyapunov 指数大于零，系统产生混沌运动。

图2 参数∈(0.0005,20)变化的分叉图和最大Lyapunov指数图

2 轧机厚度混沌系统自抗扰控制器设计

令x1=x,x2=ẋ，可将式（2）转化为如式（3）所示的二阶系统。ADRC控制器结构如图3所示。

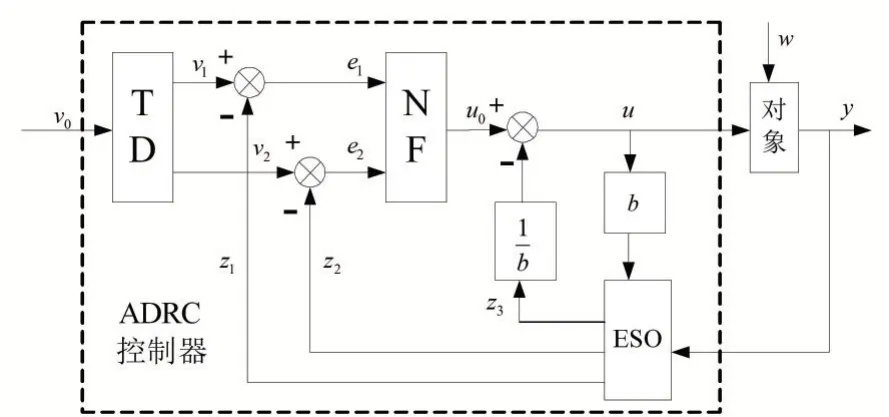
图3 二阶对象ADRC控制器结构

其中，w(t)为系统外部扰动，u为控制量，b(t)为控制放大系数，y为控制器输出，f(x,ẋ,w(t),t)是包括“内扰”和“外扰”的“总扰动”信号。

2.1 跟踪微分器

v0(t)为控制目标，v1(t)为安排的过渡过程，v2(t)为过渡过程的微分信号。其表达式为：

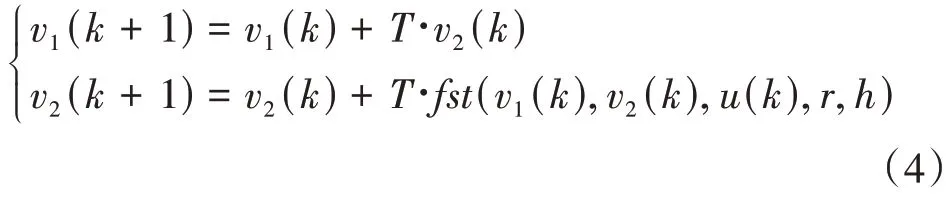
其中，T为采样周期，u(k)为控制器第k个采样时刻的控制信号；r为决定跟踪快慢的参数；h为影响滤波效果的参数；fst(r,h)为最速综合函数，如式（5）所示:

2.2 扩张状态观测器

选取信号u(k)和y(k)为其输入信号。其表达式为：

其中，e=z1(k)-y(k)，且

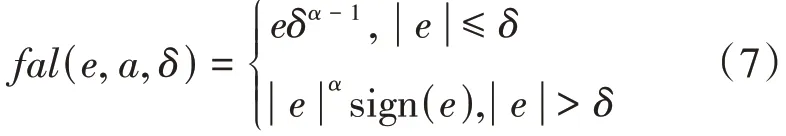
其中，z1、z2用于跟踪被控系统状态x1、x2；z3用于估计被控对象的扰动量，并反馈给控制量u。

2.3 非线性控制率

其表达式为

其中，e1、e2是误差和该误差的微分。实际控制信号u中的-z3/b项将会对被控对象的扰动和不确定性进行动态补偿。

3 系统仿真研究

3.1 阶跃响应实验

根据实际需要，选取ADRC 参数为：r= 10，h= 0.01，T= 0.01，a=[0.75,1.25]，b= 1，δ= 0，β01= 100，β02= 65，β03= 80，β1= 100，β2= 10。

在α= 0.05，β= 0.08，γ= 0.03，δ= 0.05，= 0.8时，系统（2）是混沌的，响应值取5 × 10-6，在t= 25 s 时，其阶跃响应曲线如图4 所示。由图可见经过ADRC 控制后，系统很快消除混沌状态并进入稳定状态。

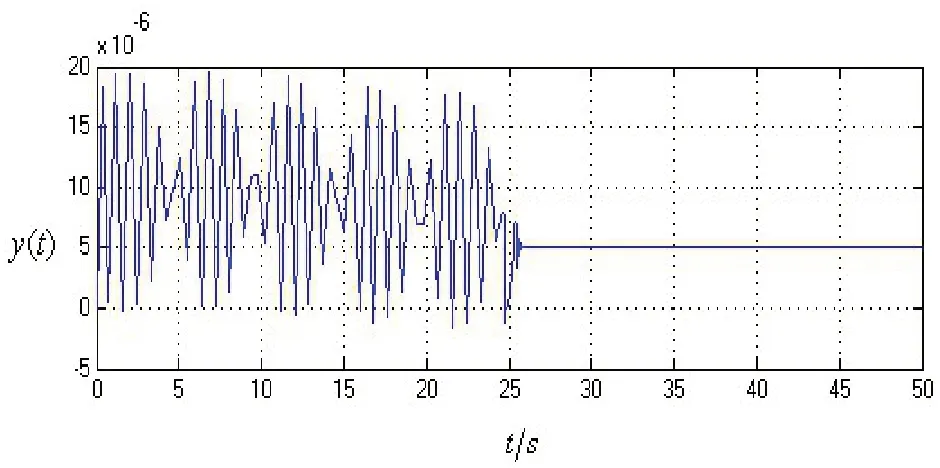
图4 系统响应曲线

3.2 抗干扰实验

在t= 6 s 时加入阶跃扰动，系统响应曲线如图5 所示。由图可知，系统能够快速克服较大的干扰并趋于稳定，说明系统具有较强的抗干扰性。

图5 系统加扰动的响应曲线

4 结语

通过对板带轧机自动厚度混沌系统数学模型分析得，该系统在满足一定条件下将产生混沌特性。采用自抗扰控制方法可以有效地控制轧机AGC 系统产生的混沌，且该控制方法快速性好，稳态精度高，抗干扰能力强，具有较高的应用价值。