实践“自主·合作·交流”教学新样态——以圆锥曲线的共同特征为例*

徐进勇 (广东省广州市第九十七中学 510260)

新课程标准倡导独立思考、自主学习、合作交流等多种学习方式，强调学习是学生与情境、问题的有效互动，突出学生个性化、多样化的学习和发展需求，提高学生交流、合作的社会沟通能力，着力发展数学核心素养．[1]新课堂样态应该是一种“自主·合作·交流”型的学习组织，它既是一种课堂形态，也是一种课堂理念、课堂结构与学习机制．这种新样态课堂能将学生的外趋要求转变为内驱动力，将学生的被动学习转变为主动求索，奠定自主学习的基础，并真正建立起师生互动与共享的共同体以促进知识的流动与创新，达成学生个人成长与课堂团队整体进步的双赢目的．

“圆锥曲线的共同特征”一节在人教A版没有专门列出，只是在例题或习题中“隐约”出现，很多教师也就不再组织学习．笔者认为“圆锥曲线的共同特征”是学习圆锥曲线后的一节很好的复习提高课，值得研究．如何才能上好这节课呢？是直接给出定义强化理解，还是让学生“自由发挥”？一番思考后，笔者决定创新课堂样态．

1 教学设计

1.1 课前任务布置

情境1 公元前3世纪，古希腊学者阿波罗尼斯用一个圆锥，通过改变截面的位置产生椭圆、双曲线、抛物线三种曲线(图1)．阿波罗尼斯从几何图形的角度来研究圆锥曲线性质，但由于过多地依赖图形而给研究带来了困难．17世纪，法国数学家笛卡尔提出点的坐标和变数思想，把几何曲线转化为代数方程，通过研究方程来揭示曲线的性质，创立了解析几何．

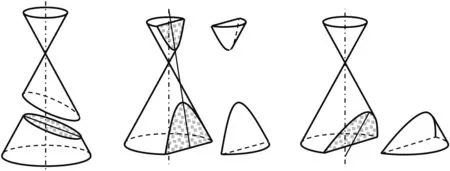
图1

情境2 圆锥曲线不仅在数学历史发展的过程中熠熠生辉，在科学文化的其他领域也闪烁光芒．如当人造天体被以不同的速度(三种宇宙速度)从地球发射出去的时候，它的轨迹分别是圆、椭圆、抛物线和双曲线(图2)，这就是物理中所讲的开普勒三大定律．

情境3 嫦娥四号于2018年12月8日在西昌卫星发射中心发射成功，在降落月球背面过程中要经过多次变轨，变轨的实施要通过数据的输入和动力制动完成(图3)．嫦娥四号实现了人类首次月球背面着陆，创造出“世界先驱者”般的成就与壮举．

图2 图3

问题椭圆、双曲线、抛物线图象的形成过程存在着密切联系，三种曲线相联的背后存在怎样的数量关系？

任务：请各位同学结合课本内容或搜集相关材料作总结或猜想，寻找三种曲线在数量上的联系与特征，探寻它们内在的统一性，并按“已有材料-猜想探索-得出结论-自我评价”的形式书写研究报告．

1.2 课堂交流展示

教师阅读学生上交的报告，发现研究方向主要聚焦三类：(1)从椭圆、双曲线定义出发思考(以下简称为“定义”)；(2)研究斜率间关系(以下简称为“斜率”)；(3)研究到定点与到定直线的距离比(以下简称为“距离”)．全班35人中研究方向大致可分为：定义法9人，斜率法6人，距离法20人．上课时按“同质”组合就座形成学习小组，前10分钟在同学习小组内交流彼此想法，加深理解，形成共识；接下来20分钟由各小组推选的汇报人通过实物投影展示研究成果；后10分钟师生共同研讨，反思提高．

学习小组1 从“定义”探索．

已有材料：到两个定点的距离和为定值(大于两定点间距离)的点的轨迹是椭圆；差的绝对值为定值(小于两定点间距离)的点的轨迹是双曲线；商为定值(不为1)的点的轨迹是圆(称阿波罗尼斯圆)，商为1的点的轨迹是直线．

猜想：到两个定点距离积为定值的点的轨迹是抛物线吗？如果是，那就太完美了！

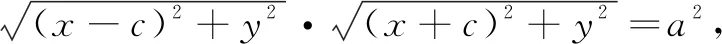
但还是很难通过描点法画出它的图象，于是想到用几何画板画图：如图4，不断改变a,c的大小关系，得到恰似一个细胞分裂成两个细胞的过程图，非常奇妙！

图4

通过上网搜索定义：这些曲线实际上是数学史上著名的卡西尼卵形线．在数学史上，到两个定点(叫做焦点)的距离之积为常数的点的轨迹称为卡西尼卵形线.卡西尼是一位出生于意大利的法国籍天文学家和水利工程师，他是第一个研究土星的人，为了纪念卡西尼对土星研究的贡献，人们用他的名字命名了用于探测土星的探测器．

得出结论 虽没达到寻找椭圆、双曲线、抛物线数量上的统一，但有意外惊喜，发现了卡西尼卵形线，明确了到两个定点的距离和、差、积、商为定值时各自点的轨迹．

自我评价 建系列方程，用方程研究曲线，几何画板帮助画图，网上查询资料，感受卡西尼卵形线很美．

学习小组2 从“斜率”探索．

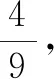
(3)(课本42页)已知点A,B的坐标分别为(-1,0),(1,0)，直线AM,BM相交于点M，且直线AM的斜率与直线BM的斜率的商是2，求点M的轨迹方程．答案：x=-3(y≠0)．

(4)(课本74页)已知点A,B的坐标分别为(-1,0),(1,0)，直线AM,BM相交于点M，且直线AM的斜率与直线BM的斜率的差是2，求点M的轨迹方程．答案：y=1-x2(x≠±1)．

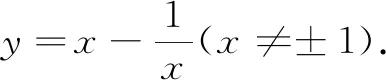
猜想：到两个定点斜率之差为定值的轨迹一定是抛物线吗？

已知点A,B的坐标分别为(-a,0),(a,0)，直线AM,BM相交于点M，且直线AM的斜率与直线BM的斜率的差是2c，探求点M的轨迹方程．

得出结论 与两个定点连线的斜率之积大于0时点的轨迹是双曲线；斜率之积小于0时(不为-1)轨迹是椭圆；斜率之积等于-1时轨迹是圆；斜率之差为定值时轨迹是抛物线．(都要去掉两个点)

自我评价 通过斜率找到椭圆、双曲线、抛物线间的数量关系，但由于斜率的条件限制，所得轨迹中都要去掉两个点，而且得出的抛物线也不是标准型，有点遗憾；认真搜集课本相关内容，通过对比能发现一些有价值的规律；从和、差、积、商的运算变化中收获新的知识；注意解题中的条件限制与等价变化．

学习小组3 从距离探索．

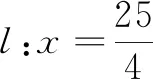
自我评价 找到了三种曲线数量上的联系，而且距离比e分别为(0,1),1,(1,+∞)的连续变化，与图形的连续变化相吻合，很开心；课本习题从(1)到(3)由特殊到一般，循序渐进；仿照课本中椭圆方程的推导过程，令a2-c2=b2，使方程化简，形式简洁，有对称美！

1.3 师生互动

展示汇报环节结束后，教师充分肯定学生的猜想及所使用的数学研究方法(用方程研究曲线)，走的路不同，欣赏到的风景也就不同，但彼此交流，让我们看到很多，想到很多！

师：针对小组3的结论，你能用更简洁的语言表达吗？

生：椭圆、双曲线、抛物线可统一为平面上到一定点的距离与到不过该定点的定直线的距离之比为常数e的动点的轨迹．

师：据此，你能求出这种统一定义下的方程吗？

如何建系，如何设点和定直线方程？方法很多，方程的形式也不同．瑞士数学家欧拉是以定点为坐标原点，定直线方程设为x=-p，此时方程是什么？学生很快计算得出(1-e2)x2+y2-2pe2x-p2e2=0．

师：用几何画板展示三种曲线的连续变化图，并说明用几何画板的制图原理(进一步突出统一 定义)．

1.4 课堂小结

平面上到一个定点的距离和到一条定直线的距离之比是一个常数e的点的轨迹是圆锥曲线，统一方程可写为(1-e2)x2+y2-2pe2x-p2e2=0．研究让我们看到,只有抓住共同的本质，才能用统一的观点、统一的语言来描述不同的事物．这让我们有一种“透过现象看本质”的快感，使我们领略到数学的“统一美”．

2 课堂新样态特征分析

2.1 课堂教学要充分尊重学生思维

好的数学教学活动应突出数学的特点和学生的思考，揭示数学知识产生的自然性与合理性，要基于感性发展理性．本节课的设计就是突破“直接化”的方案，在情境与问题的驱动下，突出学生的自然想法，如定义中到两个定点的距离和、差、商研究了，为什么不研究“积”？嫦娥四号变轨的实施要通过数据的输入和动力制动完成，那么圆锥曲线图形连续变化背后的数据又是什么呢？椭圆与双曲线定义、性质联系较为紧密，似乎与抛物线有些疏远，抛物线有准线，椭圆与双曲线为何没有？等等．不同的疑问，有不同思考；不同的人，有不同的思维方式；不同基础的学生，有不同的思维层次．但所有学生都是在探究自己想要解决的问题.学习有兴趣，主动性就很强，经历过探究过程，才能积累知识和方法，获得理智和情感体验，这就是最好的学习方式．尊重学生思维的教学要做好以下几点：(1)充分了解学生已有的认知基础，如课前教师要认真批阅学生的研究报告或作业，明确学生的认知起点；(2)尊重学生的情感起点，即教师要明白学生想知道什么、渴望解决什么；(3)尊重学生对知识建构的思维习惯，关注新旧知识之间的联系，形成自然的思维发展链条，如教师针对学习小组3所进行的适时拓展；(4)尊重学生个性差异，关注课堂新的生成，允许并鼓励学生的个性思维在课堂流淌，本节课安排3个小组分别展示，就是充分尊重学生的个性化思维，使课堂焕发出活力．

2.2 着力培养学生的自主发展能力

教学中教师先创设学习情境，提出目标与任务.学生课后学习的空间与时间是开放的、自由的，带着自己的疑问查阅课本或上网搜集资料，也可以借助其他工具(如几何画板)进行自主学习.这一目的是要让学生在学习中经历：观察分析数学事实，提出有意义的数学问题；搜集整理相关素材，归纳猜想、探求适当的数学结论或规律；给出科学合理的解释或进行理性的证明；反思探索过程，通过检验优化研究方案，从而获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验(四基)，提高从数学角度发现和提出问题的能力、分析和解决问题的能力(四能).与传统式学习相比，“自主·合作·交流”型学习更强调学习主体对材料的搜集与感悟，强调研究小组或团队的合作交流与共同进步，这些都是新时代公民必备的素养．因此，教学中教师要充分相信学生、引导学生，逐步引领学生走上自主学习与发展的道路．

2.3 合作交流是新样态课堂的主旋律

课堂教学是课堂活动的教学，课堂活动包括师生交流、展示、探究等．叶澜教授认为，在教学过程中，教师不仅要把学生看作“对象”“主体”，还要看作是教学“资源”的重要构成和生成者．学生在课堂活动中的状态，包括他们的学习兴趣、积极性、注意力，学习方法与思维方式，合作能力与质量，发表的意见、建议、观点，提出的问题与争论乃至错误的回答等，无论是以言语还是以行为、情绪方式的表达，都是教学过程中的生成性资源．有了这种“活资源”的意识，教师才不会把学生在课堂中的活动、回答看作是一种对教师教的配合，而是看作对教的过程的积极参与和教学过程创生的不可缺少的重要组成部分．[1]本节课的教学设计主旨就是学生的3种不同研究方向、方式、结果通过分组展示给全班同学，并让各种意见获得充分解释，使学生在交互学习中完全明了背后的道理．正如美国小说家华莱士所指出的，教育的目的，不是学会一堆知识，而是学会一种思维的方式．教师在教学中要积极为学生创建交流互动的平台，让学生敢说、会说且说得精彩，真正实现教师组织下的学生思维资源的共赏，体现学习不仅是个体的行为，也是集体努力的结果．

2.4 努力实现课堂教学中的文化育人

文化属性是课程知识的基本属性，挖掘课程知识的文化元素，充分表达知识的文化属性，是课堂教学中文化育人方式的前提条件．本节课的教学设计从历史和现实两种情境揭示知识的文化属性，通过“自主·合作·交流”展示学生不同的思维历程来表达教学过程作为一种文化实践的过程，并突出其中的人与事，切实在学生的知识学习过程中开展文化导入，引导学生开展文化体验、文化体认、文化体悟，感受数学的形式美、统一美、简洁美，并在探索过程中发展学生的数学文化积淀、人文素养和人文情怀．课堂教学不应仅仅把知识作为一种事实或结论告诉或传递给学生，还需对具体知识进行深入的文化分析，引导学生探究知识的文化属性、文化思想、文化精神和文化思维方式，体现知识对学生的文化影响力，真正达成“以文化人”的目的．[2]