基于电力大数据的企业复工电力指数研究与应用
2021-03-13
(国网浙江省电力有限公司,杭州 310007)
0 引言
2020 年初,为有效控制新冠肺炎疫情的传播、蔓延,从中央到各地政府纷纷出台了严厉的管控措施,严格限制人员流动并对企业的复工复产进行重点监控。春节过后,受疫情影响,人员流动率和企业复工率仍然较低,对国民经济的高速发展造成较大影响[1]。为将新冠肺炎疫情影响降到最低,保持经济平稳运行和社会和谐稳定,努力实现党中央制定的各项目标任务,也为了辅助地方政府准确全面地掌握企业复工情况,电力公司充分利用已有的电力数据资源[2-3],通过大数据分析的方法得到各地区重点企业的复工电力指数,为各级政府制定管控决策提供依据;同时,支撑政府根据各地区疫情情况进行分类指导,有序推动各类企业复工复产。
此前,已经有相关学者基于电力大数据开展了经济发展预测、房地产景气度等相关应用研究。邓雪晴[4]研究了电力消费弹性指数的变动特点及其相关影响因素,同时以电力数据为基础对国内经济增长规律和趋势进行了探索。田传波[5]等人利用神经网络技术建立城市宏观经济走势预测模型,研究城市宏观经济发展中电力数据影响因素与城市宏观经济发展走势之间的关系。杨东伟[6]通过解析产业结构和不同能(电)耗地区消费差异这两个因素对于电力消费弹性指数变动的影响,探索了电力消费与经济增长的规律和趋势。李海[7]运用皮尔逊相关系数分析、时间轨迹分析、分布滞后模型与阿尔蒙估计法进行建模分析,研究了电力消费量与国房景气指数关系。刘玉娇[8]等人提出一种基于X13-ARIMA 季节调整算法的电力景气指数模型,对我国宏观经济发展状态进行分析。但是目前尚无基于电力数据开展复工情况分析的相关研究。
1 研究思路
本文研究对象是一个地区内能够有效组织生产的企业,小电量企业、已经报停企业以及为抗疫提供支持的各级企事业单位不在本次研究范围之内。
根据文献研究及相关实践[9-10],衡量一个地区的企业复工复产水平,一般从两方面进行考量:一是该地区已复工企业占该地区所有企业总数的比例,即复工企业比例;二是该地区复工后电量恢复到春节前的状态水平,即复工电量比例。基于此,以复工企业比例和复工电量比例为基本点,构建企业复工电力指数计算公式如下:
企业复工电力指数F=(复工电量比例×0.5+复工企业比例×0.5)×100%。
其中,对于复工电量比例,需要计算该地区企业用电量相较历史正常水平的比例,其计算公式为:
复工电量比例=统计范围内企业当日用电量总和/统计范围内企业2019 年12 月日均用电量总和×100%。
对复工企业比例,需根据企业开始复工的时间节点来判断,具体应结合企业自身用电规律进行分析,本文将针对此问题进行重点研究。
2 企业复工比例计算
判断企业春节后是否复工,需要根据企业自身用电规律进行分析。不同企业在春节期间用电规律不一致:部分企业在春节期间继续保持营业,春节后一般会继续进行相关的生产工作;其余企业在春节期间,由于员工返乡导致其停产或停工,随着春节假期的结束,逐步恢复生产,用电水平也逐渐上升。这两类企业的用电规律明显不同,需分别进行分析。
为了对企业复工复产信息进行有效的数据分析,首先需要搜集企业相关用电数据信息,具体包括企业档案数据和2018—2020 年春节前一个季度及春节后一个月的用电数据。
2.1 企业分群
2.1.1 用户分群方法
英国统计学家辛普森曾于1951 年提出辛普森悖论[11],即在某个条件下的两组数据,分别讨论时都会满足某种性质,但是一旦合并考虑,却可能导致相反的结论,换句话说,变量在不同的空间中可能与目标变量形成完全不同的相关趋势。
辛普森悖论同样会发生在电力领域:不同用户的用电规律通常有较大的差异,而春节期间是否停工决定了用户的用电规律,但如果用相同复工标准判断两类用户,将会得到错误的结论。为了避免辛普森悖论,需要将其在不同的子空间中单独进行分析。因此,根据春节用电规律将用户分群,并使用Knee point 算法对春节期间停工用户是否复工进行判断,同时可以较好地平衡局部差异优化和模型运行时间之间的关系。
根据春节用电规律进行分群的方法属于无监督模型分群。常见的模型有K-means[12-13],Kmedoids[14-16],Mean Shift[13],层次聚类[14-15],DBSCAN[16],GMM(高斯混合模型)等[17-21]。其中GMM 利用多个高斯分布对数据集进行拟合,在实践中有更好的表现,因此本文选用GMM 进行用户分群。
GMM 本身是一种概率式的聚类方法,设xi(i=1,2,…,m)为第i 个数据观察值,假设样本服从高斯混合分布:
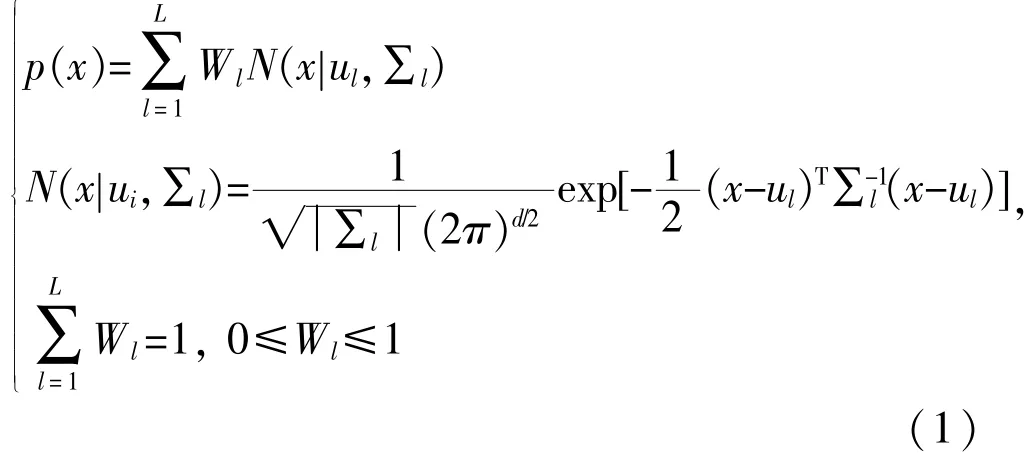
2.1.2 基于GMM 的聚类分析
具体步骤如下:
(1)初始化高斯混合分布的模型参数Wl,ul,∑l。
(2)计算样本Xj由各混合成分生成的后验概率,即观测数据xj,引入一个隐变量zj∈{1,2,…,k},表示得到样本xj的高斯分布模型。由第i个分模型生成的概率为p(zj=),记为γji=
(3)计算新的模型参数:
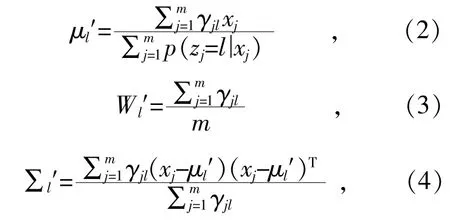
(4)按照新的模型参数重复步骤2 和步骤3,直到满足终止条件。
2.1.3 聚类分析结果
收集统计范围内所有有效企业的电量信息、基础档案信息,构建春节用电比例特征K 和日电量方差N,其中:
K=春节期间平均日电量/春节前3 个月平均日电量。
N 指春节期间平均日电量方差,包括春节前3 个日电量方差。
使用GMM 算法进行聚类,由于模型不一定刚好将用户聚为2 类,需要根据模型收敛情况,选择合适的聚类数m,最终聚类结果如图1 所示。
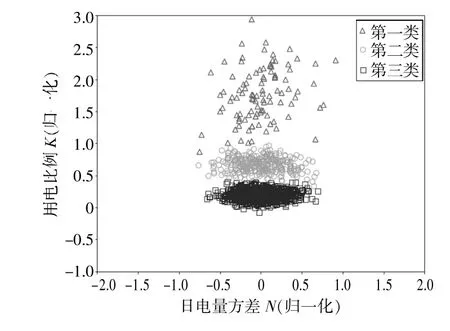
图1 GMM 算法聚类结果
根据聚类的收敛情况,选择最适合的聚类数为3 类。由于各类企业的日电量方差差异不明显,本次仅使用春节用电比例K 划分用户,各类企业春节用电比例K 如表1 所示。
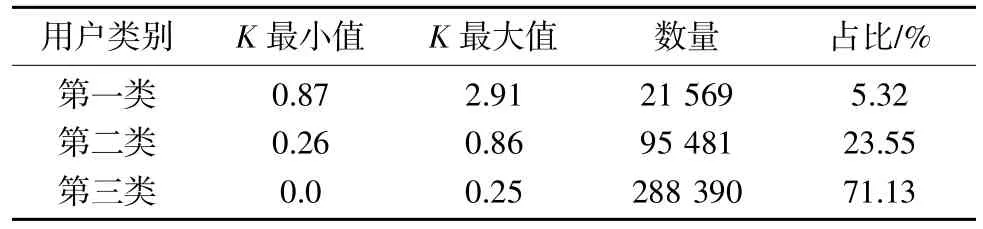
表1 GMM 算法聚类结果
根据聚类结果以及业务目标,合并第一类和第二类群体,将企业划分为春节停工企业和春节不停工企业,具体如表2 所示。

表2 基于聚类结果划分企业类别
根据聚类结果,用电比例大于0.26 的春节期间不停工企业,在节后停工的概率较低,因此直接默认其节后复工;对于春节停工的企业,可利用相关的拐点算法进行分析。
2.2 企业复工判断
2.2.1 企业复工判断标准及算法原理
企业用电水平会随着经营情况发生变化,形成一条具有明显波动性的用电曲线。春节停工企业在春节期间处于较低的用电水平,到复工节点会出现电量骤增的现象,届时用电曲线将会出现明显的拐点。基于此特征,本文采用Knee point算法判断历史上同时期春节后其用电量出现拐点的时间,确定相对于正常生产时达到复工状态的用电量,并计算其与春节前平均用电量水平的比值,以此作为企业复工的判断标准。
Knee point 算法[22-24]的基础定义如下:
对于任何连续的函数f(x),存在一个标准的闭合形式Kf(x),它将f(x)在任何点的曲率定义为其一阶和二阶导数的函数:
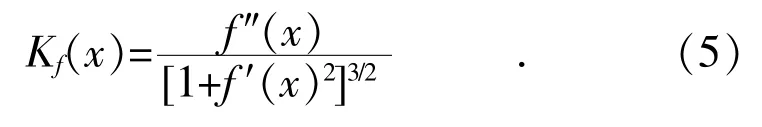
给定一组(xi,yi),将曲线基于点(xmin,ymin)和(xmax,ymax)构成的直线顺时针旋转θ,则最大曲率点的数据集近似为曲线中局部最大值的点集,即数据曲线变平坦时,曲率变小,拐点也就会被检测到。因此,模型最后返回曲率最大的点,即达到识别曲线拐点的效果。
2.2.2 Knee point 算法步骤
Knee point 算法具体步骤如下:
(1)使用多项式插值法对源数据集进行拟合,尽可能保持源数据集的形状,也可用到如指数加权移动平均等方法。用Ds表示平滑曲线上点(x,y)的有限集:
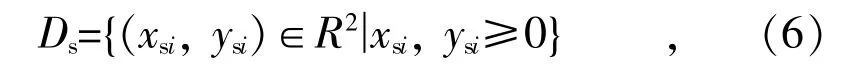
式中:xsi,ysi为给定的x,y 拟合后的数据。
(2)为消除异常值对平滑曲线中最大曲率的影响,对平滑曲线上的点进行归一化处理,用Dsn表示处理后的数据集,则有:

其中,
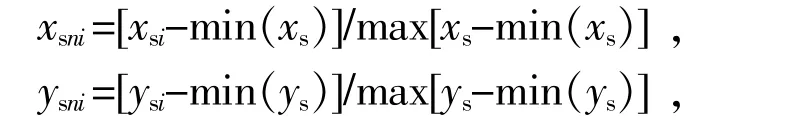
式中:xsni,ysni分别为归一化处理后的x 和y 值;xs,ys分别为x,y 值形成的序列;min{xs},min{ys}指的是xs,ys序列中的最小值。
(3)寻找平滑曲线何时从平缓变化到急剧下降,设立差分曲线数据集,用Dd代表x 和y-x 的差分数据集,则有:
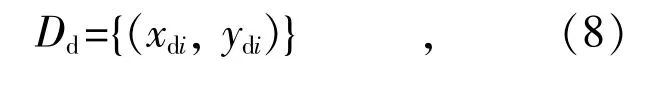
其中,
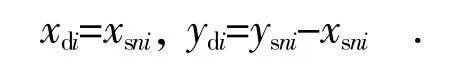
(4)寻找标准化曲线中的拐点,对曲线下降处,则需要计算差分曲线的局部最大值,这些局部最大值点最后都有可能成为源数据曲线的拐点,将可能的局部最大值点数据集表示如下:
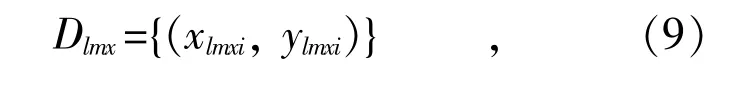
其中,
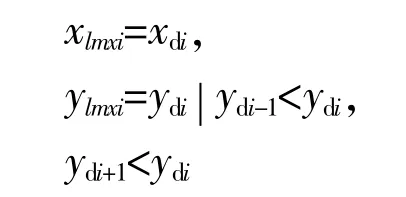
式中:xdi,ydi为差分过后的数据。
(5)对于差分曲线中计算得到的每个局部最大值xlmxi,ylmxi,用连续x 值与模型敏感度参数S之间的平均差定义唯一的阈值Tlmxi。敏感度参数S决定了拐点检测的快慢及检测出的数量,阈值计算公式如下:
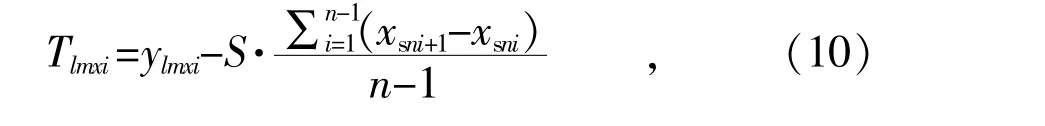
式中:Tlmxi为阈值;S 指的是对于一个曲线,输出的拐点数,S 越大,模型越敏感,一般设为1。
(6)进行拐点检测时,如果在达到差分曲线下一个局部最大值之前,任意差值(xdj,ydj)低于(xlmxi,ylmxi)(其中j>i)处的阈值y=Tlmxi,则Knee point 算法在x=xlmxi处存在拐点。如果在达到y=Tlmxi之前,差值达到局部最小值并开始增大,则将阈值重置为0,等待下一个局部最大值。
2.2.3 应用实例
应用上述理论方法进行实例分析,具体结果如下:
(1)对企业用电数据进行平滑处理,接着利用Knee point 算法识别2018 年、2019 年春节期间拐点日期及当日日电量T1 和T2,结果如图2 所示。基于Knee Point 算法分析可知,2018 年春节期间,某企业在2 月21 日电量突增,表明该企业此时开始复工,T1=1 786 kWh。同理,由图3可知,2019 年春节期间,该企业于2 月10 日开始复工,T2=1 874 kWh。
(2)分别用T1,T2 除以2018 年及2019 年春节前30 天日均电量,得到相应的企业复工比例K1和K2,再求均值得到该企业复工用电比例K=0.642,并以此为阈值对2020 年该企业是否复工进行判断。例如,2020 年2 月11 日某企业日电量为2 690 kWh,其春节前30 天的日均电量为2 798 kWh,计算得2 690/2 798=0.961>K,则判断该企业已复工。
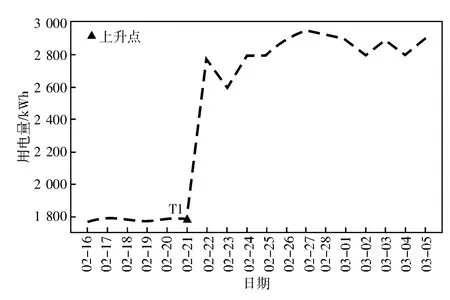
图2 基于Knee Point 算法判断企业2018 复工情况
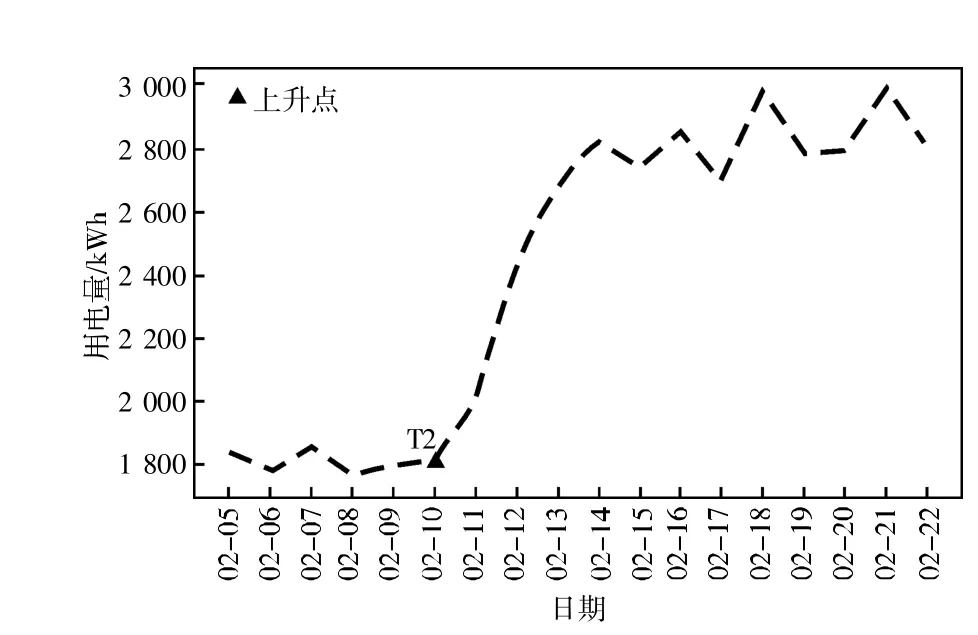
图3 基于Knee Point 算法判断企业2019 复工情况
针对统计范围内的数据,采用上述方法对每个企业的复工状态进行研判,得到浙江全省复工企业数量,最终计算得到区域内企业复工比例。
(3)结合复工电力指数计算公式(1),计算出浙江全省企业的复工电力指数。
2.3 复工结果验证
在全省范围内通过电话调研的方式,按照企业规模和行业类别随机抽取500 家企业进行验证,得知复工时间准确率达96.3%,验证了本文所提算法的有效性及准确性。
3 企业复工电力指数的应用分析
基于前文所述企业复工电力指数计算方法,评估浙江省范围内企业复工复产情况,为政府疫情防控工作提供参考。
3.1 全省复工情况分析
根据前文提出的企业复工电力指数计算方法,得到浙江各地企业复工情况如图4 所示。可以看出,指数最高的为舟山(71.33),最低的为台州(21.89)。经计算,2 月16 日(正月廿三)浙江省复工电力指数为36.01,相较2 月15 日(正月廿二)的32.94 上升明显。
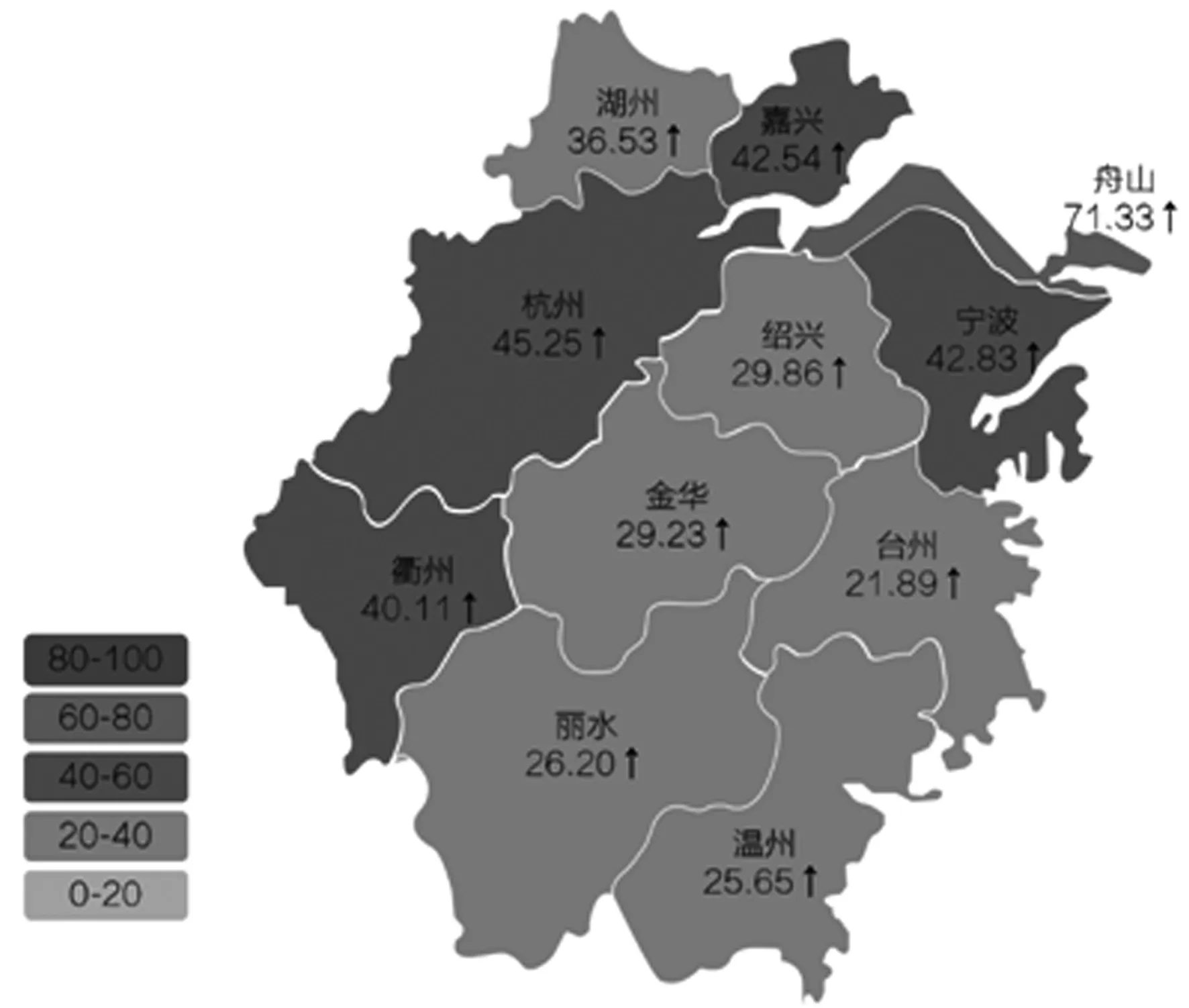
图4 浙江各地2020-02-16 企业复工电力指数分布
为了研究全省企业复工趋势,连续计算每日的复工电力指数,结果如图5 所示。对比发现,2020 年正月同时段企业复工电力指数与2019 年差距较大,2019 年正月十七至正月廿三全省复工电力指数增长速度较快,2020 年此段时间仍处于疫情防控状态,指数以较稳定的速度缓慢上升。
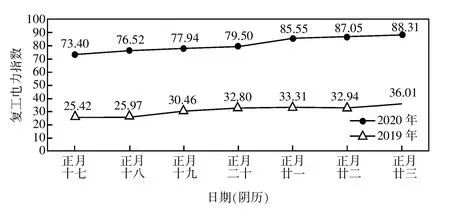
图5 2019 年、2020 年浙江省企业复工电力指数趋势对比
根据分析需要,对复工电力指数分析对象作进一步细化,剔除国家行政机构、医院等公共服务及管理组织企业(7.3 万户),调整后得到新的企业复工电力指数如图6 所示。对比图5 可知,剔除相关公服企业后,2020 年企业复工电力指数均有所下降,这说明当前复工的企业中,医院等公共服务机构较多。
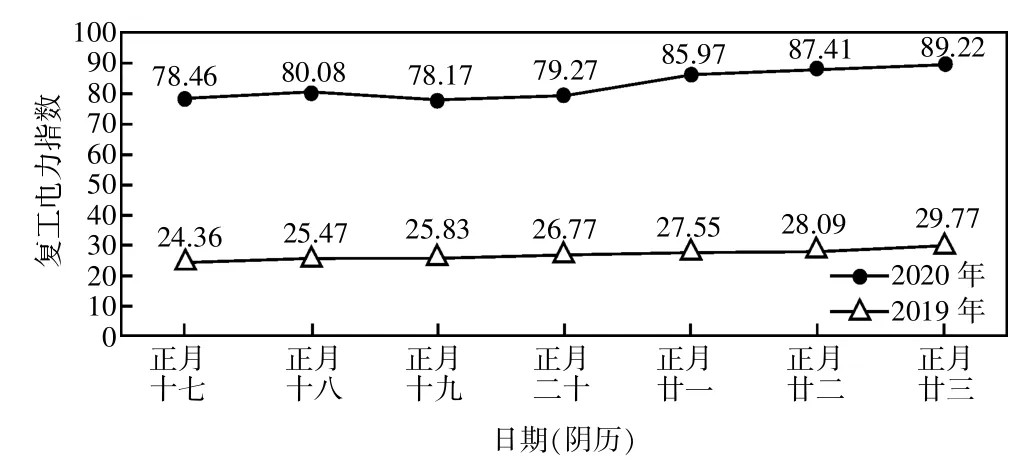
图6 2019 年、2020 年浙江省企业复工电力指数趋势对比(剔除公服企业)
3.2 各地市、县(区)复工情况分析
图7 给出了浙江各地市企业2019 年、2020年同期复工电力指数,可以看出,2020 年正月廿三浙江各地市企业复工电力指数情况较2019 年同期均有明显下降。通过对比分析可知,受疫情影响,目前浙江各地市企业复工指数虽然稳步上升,但总体复工情况相比2019 年,还有较大的提升空间,后续根据疫情的防控情况,政府可以出台相应的鼓励复工举措。
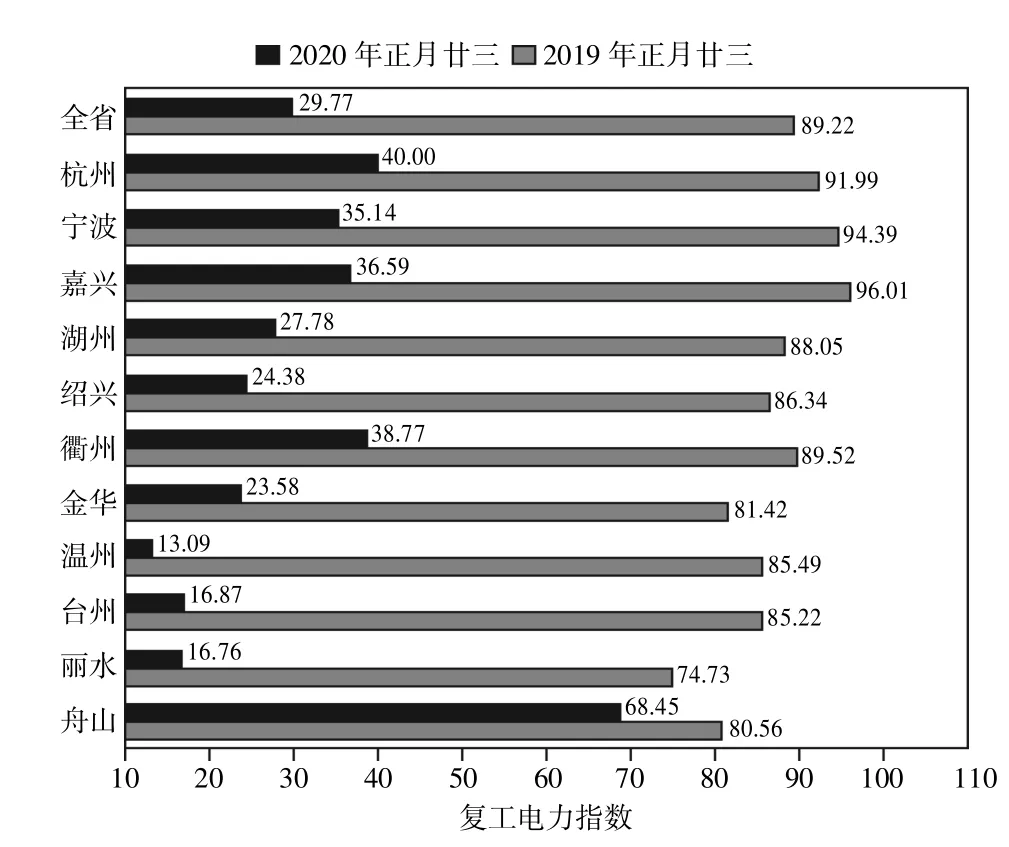
图7 浙江省各地市企业2019 年、2020 年同期复工电力指数对比
同时,由于各个地区疫情防控程度不同,后续建议因城施策,各地根据实际情况制定复工举措,例如:温州由于受到疫情影响比较严重,因此复工受到较大影响,后续应采取更加灵活的复工措施;舟山企业受疫情影响较低,复工指数较高,是因其属于海岛型城市,隔离方便。
4 结语
为有效辅助政府对新冠疫情形式下企业复工复产情况进行管控,供电公司充分发挥自身电力数据资源优势,在深入开展数据挖掘的基础上,提出了企业复工电力指数的具体计算方法。基于企业复工电力指数计算方法,对浙江省的企业复工情况进行测算,并将其与实际情况进行对比分析,验证了所提计算方法的有效性。实际应用表明,本文提出的企业复工电力指数可以准确全面反映企业的复工状况,为后续企业复工相关政策的制定提供重要支撑。
