不同风向条件下输电塔风致响应数值模拟

2021-03-13吕洪坤刘孟龙汪明军应明良樊建人

浙江电力 2021年2期

吕洪坤，刘孟龙，池伟，汪明军，罗坤，应明良，樊建人

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.浙江大学能源工程学院，杭州 310027；3.杭州意能电力技术有限公司，杭州 310012）

0 引言

随着我国经济的快速发展，用电需求不断增长，这对输电工程提出了越来越高的要求。作为高压输电工程中的主要承重设施，输电塔正逐渐向大跨越、高塔身、高电压等级的方向发展[1]。轻质、高柔是常见的格构式输电塔所具有的结构特征[2]，这使得格构式输电塔对风荷载较为敏感，在大风条件下塔体易出现较大的响应，甚至关键构件断裂从而引起倒塔事故，对电网的安全运行产生危害。因此，研究输电塔风致响应特征具有重要的实际工程指导意义，对输电塔的设计工作有直接帮助。

实际工程中，大量的高压输电塔具有显著的横向结构特征，如长横担、猫头塔塔头等，对风向较为敏感，在不同风向作用下体现出不同的风致响应特征。目前，关于不同风向作用下输电塔风致响应特征已经有一些学者开展了研究并取得一定的成果。谢华平等[3]基于CFD 方法分别对猫头塔塔头和塔身进行了不同风向下风荷载研究，结果表明塔身风压随风向变化不大，而塔头风压有显著变化，当风向与导线夹角为15°时，其结构阻力系数最大。党会学等[4]对格构式三角输电塔塔体结构构建了结构化网格模型，进行了不同风向的风场CFD 模拟，研究了其在不同风向条件下空间结构的屏蔽特性和风荷载特征，计算结果表明角钢折角朝向来流方向比背向来流方向的屏蔽作用更强。Jonas 等[5]以Fluent 对塔体周边区域进行了风场模拟，研究了不同风向条件下塔体结构的阻力系数，提出采用多孔介质模型简化网格模型的方法，通过和经典CFD 方法以及风洞试验进行对比确定了此方法的可行性。潘峰等[6]根据IEC 规范以及BS 规范中风荷载模型计算了不同风向作用下塔身和横担的风荷载分配系数，分析了其在不同风向条件下的塔体结构风荷载特征。

综上所述，目前大量的研究工作主要聚焦在对塔体结构在不同风向下承受的风荷载特征分析，对塔线体系最不利风向问题仍缺乏比较系统的研究。而现今已有一些研究表明塔线耦合作用对输电塔风致响应特征有着不可忽视的影响[7-8]，且实际工程中各种档距的塔线体系都存在，目前相关研究成果对实际工程项目的参考价值有限。围绕这些问题，本文以温州某输电线路为研究对象，根据实际参数分别建立无导线塔体与不同档距塔线体系有限元模型，对比分析了塔线耦合作用、塔体两侧的不同档距对各风向条件下结构风致响应特征的影响，并且得出了一些具有工程指导意义的研究结论。

1 工程参数及有限元模型

为了便于开展输电塔在不同风向条件下风致响应数值模拟研究，本文首先根据输电线路的有关工程参数，选取型号为SJC1 的输电塔体型，建立输电塔及塔线体系有限元模型。如图1 所示，输电塔结构为格构式，由等边角钢构件搭建而成，其中，主材钢材采用Q420 和Q345，辅助材钢材采用Q235。塔体沿高度方向分为10 个塔段，塔体总高度为44.5 m，地面到电杆最低挂线距离，即呼高为27 m。如图2 所示，输电导线为双分裂钢芯铝绞线JL/G1A-400/35，地线为铝包钢绞线JLB40-150。

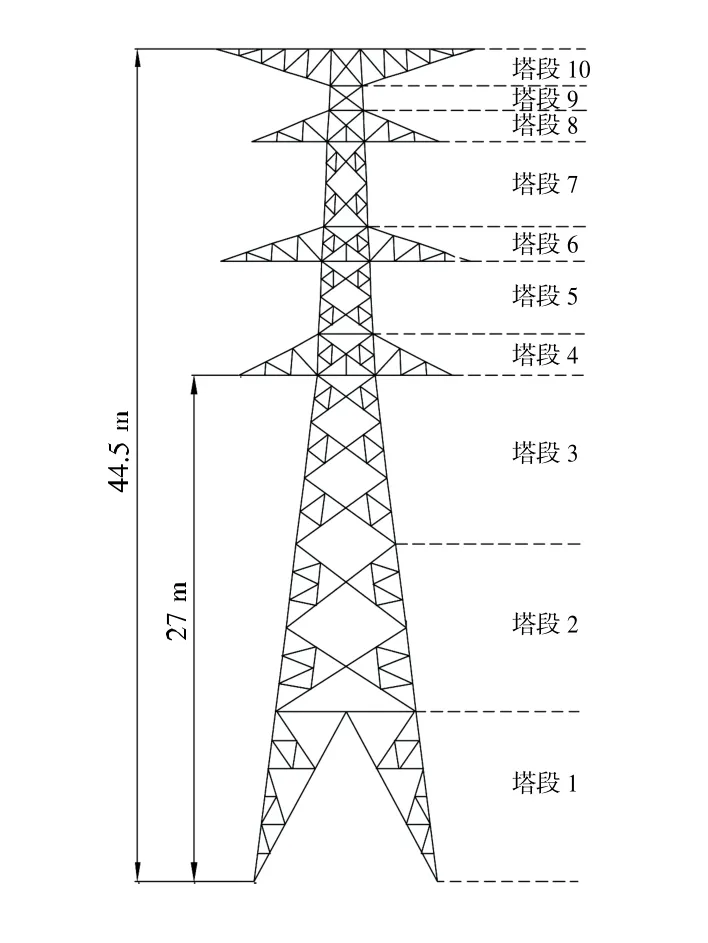
图1 输电塔结构

图2 输电塔线耦合体系有限元模型

本文根据确立的输电塔结构参数以及导地线参数（见表1）分别建立了无导线输电塔和一塔两线塔线体系有限元模型。在输电塔有限元模型中，采用梁单元BEAM188 模拟角钢，并通过控制每个梁单元的朝向，使得角钢结构符合实际设计情况。在塔线体系有限元模型中，采用LINK10单元模拟输电导线，使其具有明显的柔性特征，更符合实际情况。为便于计算，模型对导线进行了一定的简化处理，根据横截面面积等效原则将双分裂导线简化为单根整体导线[9]。本文通过悬链线公式计算输电导线各节点初始位置，并将导线模拟成小段LINK10 单元连接而成的单元组合体，初步建立了输电导线的有限元模型[10]。如图2 所示，根据上述方法分别构建不同档距（档距L=300 m，600 m，800 m）的输电塔线耦合体系有限元模型，而无导线输电塔模型如图1 所示。

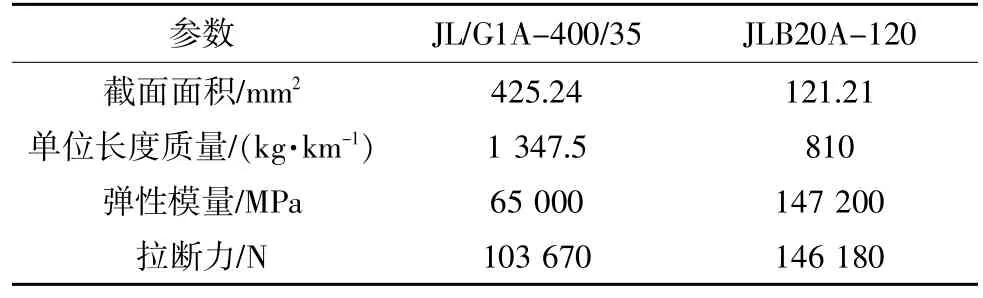
表1 导地线物性参数

2 风荷载模拟

在风工程领域的研究中，为了研究实际风的静态特征和动态特征，经常将其分为平均风以及脉动风[12]。我国建筑载荷规范[12]和国际电工协会规范IEC 60826—2003[13]均使用指数型风速剖面，此次风荷载模拟采用相同的指数型风速剖面，计算公式如下：

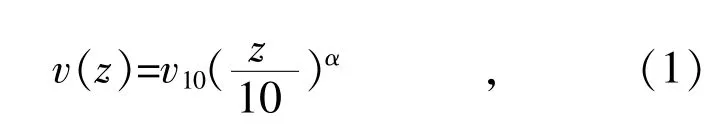
式中：v（z）为z 高度的计算风速；v10为标准高度10 m 高处的风速，取40 m/s；α 为与当地地形相关的系数，根据我国规范取值0.15。

为了得到各高度对应的脉动风速，本文基于规范使用的Davenport 风谱，结合谐波合成法进行脉动风场模拟，绘制了高度为10 m 处的脉动风速时程曲线和模拟谱值，如图3 所示。图3（b）展示了风荷载模拟谱值围绕着其目标谱值上下波动，整体变化趋势相一致，可以验证由模拟得到的脉动风速时程数据可靠合理。

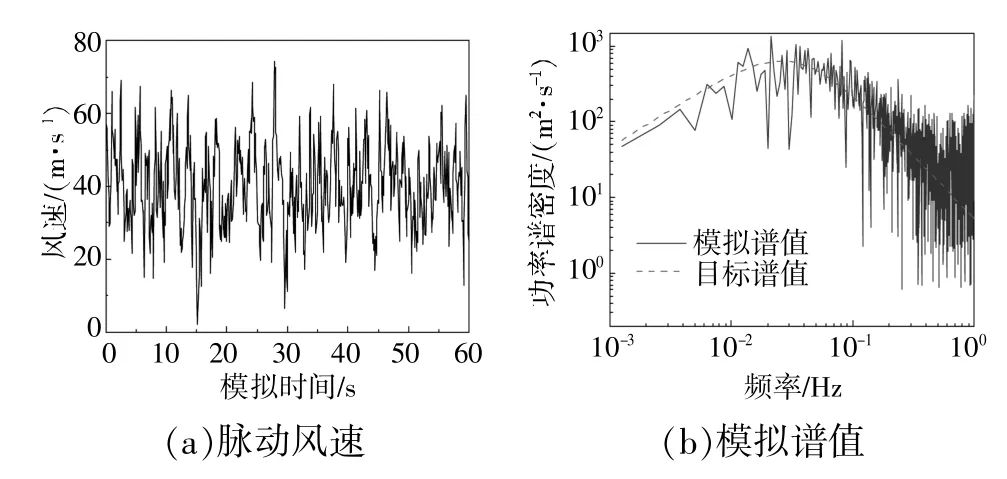
图3 脉动风模拟

如图1 所示，将输电塔结构沿高度方向划分为10 个塔段，并模拟计算每个塔段的结构参数以及承受的风荷载，从而更加准确地计算整个塔体的风荷载。为了较为细致地研究不同风向作用下的风致响应，本文根据英国规范BS EN 50341-1:2012[14]和国际电工协会规范IEC 60826—2003得到输电塔塔身和横担在风向角为0°，15°，30°，45°，60°，75°，90°风向条件下的风荷载分配系数，进而模拟此7 种风向作用下塔体和导线承受的风荷载。

如图4 所示，为了方便后续对结果进行分析，本文对塔体主材进行编号，并采用英国规范BS EN 50341-1:2012 规范中对风向角的定义，即来流风向与输电塔横担长轴向的夹角为风向角。

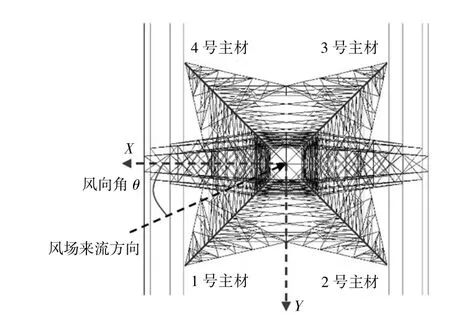
图4 风向角定义及主材编号

此外，本文参考IEC 60826—2003 规范对于塔身结构在不同风向下所承受的风荷载进行模拟，参考BS EN 50341-1:2012 规范对于横担结构在不同风向下所承受的风荷载进行模拟。塔体、横担及导线所承受风荷载可按如下各式进行计算。

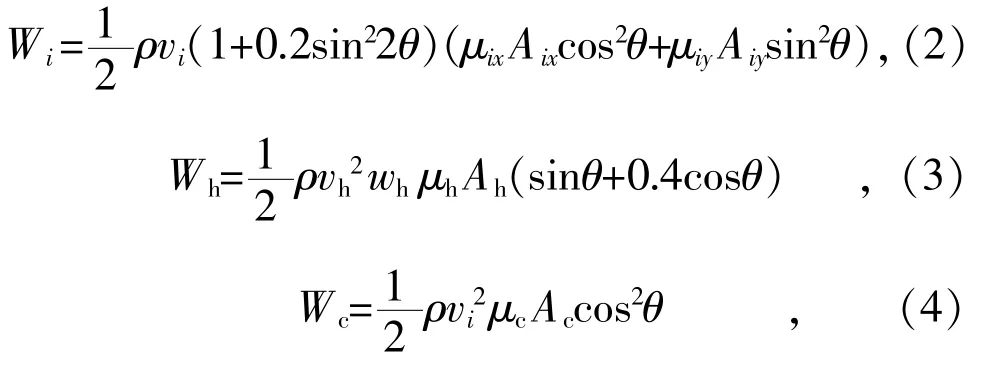
式中：Wi，Wh和Wc分别为塔段i、横担和导线所承受的风荷载；vi，vh和vc分别为塔段i、横担和导线风荷载对应位置计算风速；ρ 为空气密度；Aix，Aiy分别为塔段i 的x 方向迎风面投影面积和y 方向迎风面投影面积；μix和μiy分别为其对应投影面积计算时使用的体型系数；Ah和Ac分别为横担和输电导线的最大迎风面投影面积；μh和μc分别为横担和导线的体型系数；θ 为风场来流和横担长轴向的夹角。

3 结果与分析

本文对风向角0°，15°，30°，45°，60°，75°，90°共7 种风向条件下输电塔及不同档距（L=300 m，600 m，800 m）的塔线体系分别进行风致响应稳态分析以及瞬态分析，对比计算结果，分析塔线耦合作用和塔体两侧档距对最不利风向角的影响，并研究不同风向条件下的风致响应特征。

3.1 塔线耦合作用对最不利风向角的影响

本节主要分析塔线耦合作用对主材轴力最不利风向角的影响。如图5 所示，本节首先根据稳态分析模拟结果提取了无导线模型塔体在0°，45°，60°，90°风向角作用下塔体各高度主材轴力单元轴力。其中，轴力为正表示轴向拉力，为负表示轴向压力。

结合图4 风向角定义以及主材编号，对比分析图5（a）—（d）可知，风向角的变化引起了塔体结构各主材与来流风向相对位置的变化，进一步导致主材承受的轴力作用性质发生变化。结合图5（a）和图5（b）分析，当风向角为0°～45°时，背风侧2 号、3 号主材承受轴向压力，迎风侧1 号、4号主材承受轴向拉力；此时，由于风力作用对导线及塔体产生的整体力矩以及塔体自身重力作用，背风侧主材轴向压力大于同高度迎风侧主材拉力。当风向角为45°～90°时，1 号、2 号主材在迎风侧，承受轴向拉力，3 号、4 号主材在背风侧，承受轴向压力；此时主材承受的轴力作用性质发生变化。

进一步分析，塔体各主材高度所受轴力大小随风向角的改变而改变，而不同风向作用下，塔体主材轴力最大值均出现在塔体背风侧接近塔脚横隔面位置处，即背风侧主材高度为7.5 m 左右处。

此外，分析塔体同侧主材轴力随风向角的变化情况可知，当风向角为0°和90°时，迎风、背风同侧主材轴力基本相同，共同分担塔体载荷，主材轴力最大值较小。而在其他风向角情况下，同侧主材轴力承受着不均等的载荷，顺风向最上游主材，即1 号主材承受更大轴向拉力，而最下游主材，即3 号主材承受更大轴向压力，塔体最大主材轴力相比于0°和90°有所增大。将同高度各主材轴力相比较，顺风向最下游3 号主材所受轴力最大。

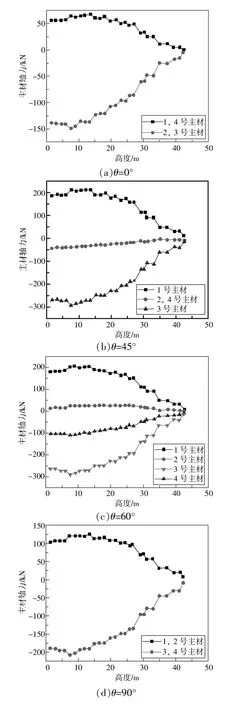
图5 输电塔各高度主材单元轴力

当风向角为45°时，风场来流方向与塔体结构对角线重合，因此，顺风向中游主材，即2 号、4 号主材所受轴力基本相同，主材轴力最大值最小。此时，顺风向上游1 号主材承受最大主材拉力，顺风向下游3 号主材承受最大主材压力。

为了分析塔线耦合作用对最不利风向的影响，本节选取档距300 m 的塔线体系模型与无导线模型进行比较分析，并绘制两个模型在不同风向条件下3 号主材承受轴力随高度变化曲线，如图6 所示。由图6（a）可知，对于无导线模型，当风向角由0°增大到45°时，最大主材轴力随之增大；当风向角由45°增大到90°时，最大主材轴力随之减小，最大主材轴力在45°有最大值。

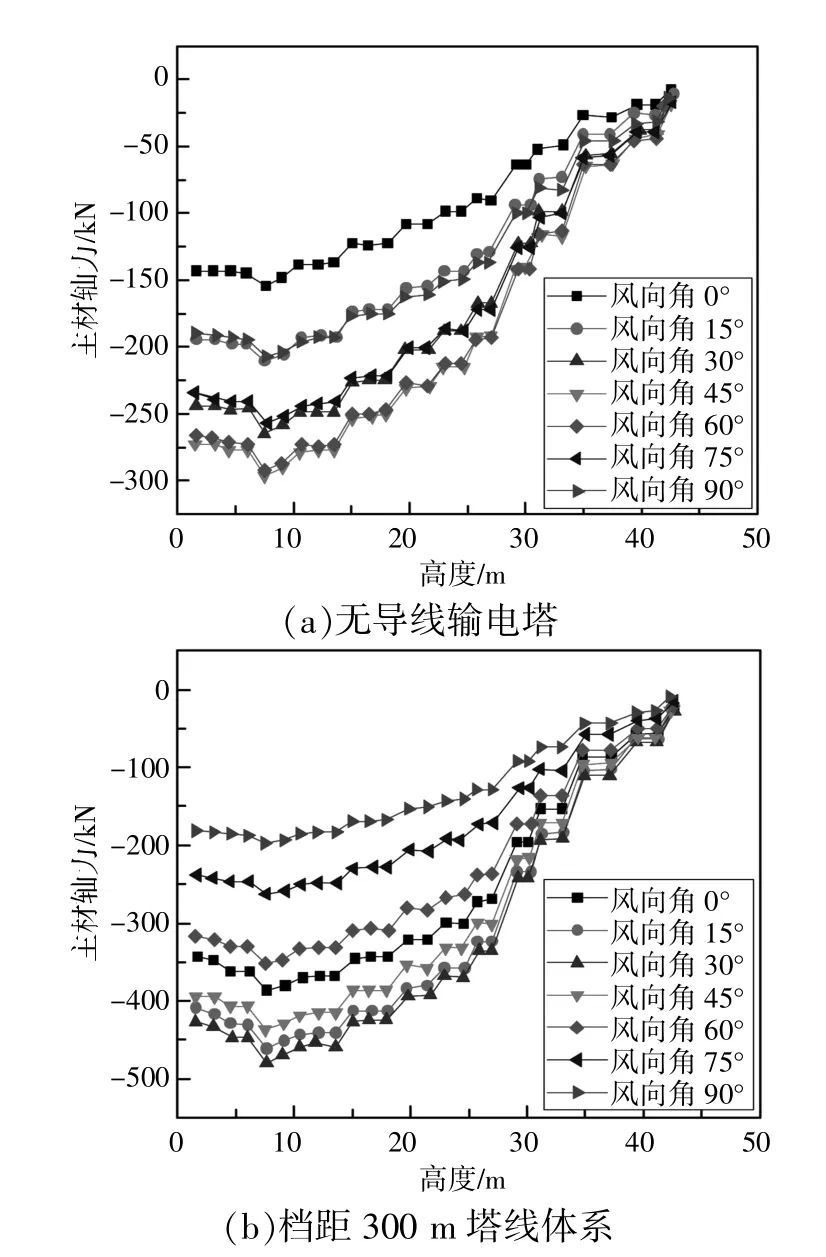
图6 不同风向条件下各高度最大主材轴力

从图6 可以看出，档距300 m 塔线体系模型和无导线输电塔模型的主材轴力随高度的变化关系类似：同一风向条件下，随着高度增大，主材轴力整体上呈现先增大然后减小的变化规律，最大主材轴力出现在塔脚横隔面周边位置主材单元。根据前文的分析可知，无导线输电塔模型的最不利风向角为45°。分析图6（b）可知，档距300塔线体系模型主材轴力的最不利风向角为30°，此时的主材轴力最大，且此轴力值大于无导线模型最不利风向条件下的最大主材轴力。因此，考虑塔线耦合作用后，塔体在不同风向条件下主材轴力的最不利风向角以及最大主材轴力值发生了变化。导线对不同风向角的风致响应影响不同，改变了塔体响应的最不利风向条件和最大主材轴力值。

3.2 档距对最不利风向角的影响

为了分析档距对最不利风向角的影响，本节根据稳态分析计算结果分别绘制了无导线输电塔和档距为300 m，600 m，800 m 的塔线体系模型中最大主材轴力与最大位移响应随风向角的变化曲线，如图7 所示。

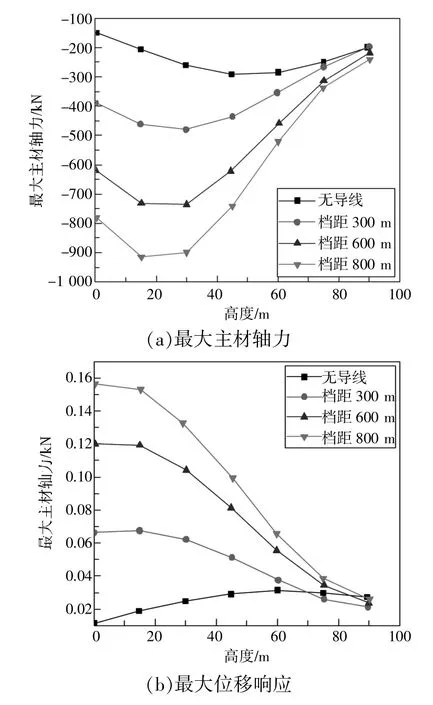
图7 不同档距塔线体系在不同风向作用下风致响应

从图7 中可以看出，塔线体系主材轴力和位移响应显著大于无导线模型，并且最大值随着档距的增大而增大。而当风向角为90°时，各模型的主材轴力和位移响应相差不大，导线带来的影响降到最低。因此，塔线耦合作用直接影响了塔体的最大主材轴力以及最大位移响应。

同时，塔体两侧档距的大小也直接影响着塔体的最不利风向角。无导线模型的最大主材轴力在风向角为45°时达到最大，最大位移响应在风向角为75°时达到最大。而对于档距300 m 的塔线体系模型，其主材轴力最不利风向角为30°，位移响应最不利风向角为15°。进一步分析不同档距塔线体系模型的最不利风向角可知，当档距增大时，塔体主材轴力以及位移响应的最不利风向角逐渐向0°偏移。档距600 m 塔线体系在风向角为15°和30°时主材轴力最大值基本相同，档距800 m 塔线体系在风向角为15°时的最大主材轴力大于30°风向角作用下的结果。而至于最大位移响应，档距600 m 和800 m 塔线体系位移响应的最不利风向角均为0°。由此可以得出结论：随着档距增大，塔线耦合作用会使得塔体响应（主材轴力，位移响应）的最不利风向角趋近于0°，即风向为横线向。此结论可用于指导工程实践，例如在设计大跨越档距的塔线体系时，应更多关注横线向风向作用下塔线体系的稳定性；而在设计小档距及塔体横向特征显著的塔线体系时，应更多重视横线向以外的其他风向作用的影响。

3.3 不同风向条件下的动力响应特征

为了研究塔体在不同风向条件下的动力响应特征，本节采用风振系数[15]和加速度RMS（均方根值）作为表征参数，其中，风振系数的具体计算公式[16]如下：

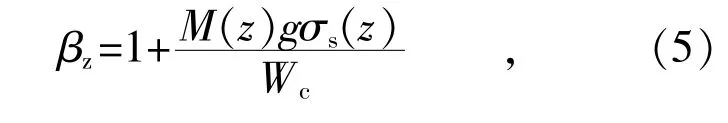
式中：M（z）为z 高度塔段对应的质量；g 为峰值因子，取3.5；σs（z）为塔体结构在z 高度的顺风向加速度响应RMS；Wc为塔段静态荷载。

本节基于Davenport 风谱进行数值模拟，得到了风速时程数据，并依此绘制不同输电塔模型（无导线模型；档距300 m，600 m，800 m 塔线体系模型）加速度RMS 以及风振系数随风向角的变化曲线，如图8 所示。

从图8 可以分析出，塔线耦合作用能够有效抑制输电塔的加速度响应。通过对比无导线模型和塔线体系模型可知，无导线模型的加速度响应和风振系数最大，其加速度响应最大值出现在风向角为60°时。在不同档距塔线体系模型中，档距越大，其动态响应越低，且加速度响应的最不利风向角均出现在风向角为45°时。

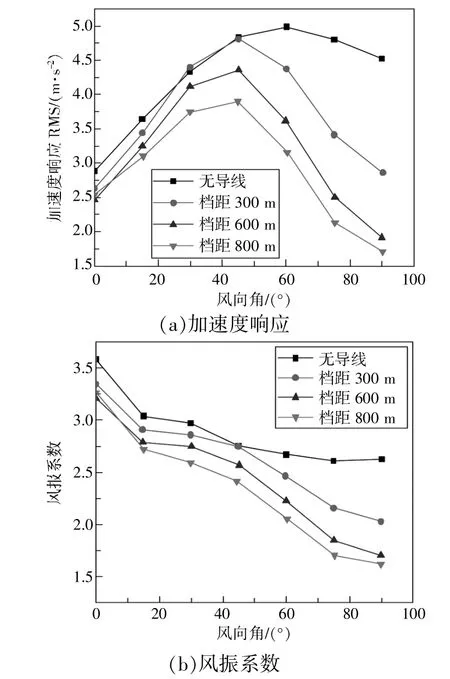
图8 不同风向条件下的动态响应

此外，分析图8（b）可得，不同输电塔模型的风振系数随风向角变化的整体规律相同：随风向角增大，风振系数减小，在顺线向、横线向风向条件时风振系数分别取最小、最大。因此，不同风向条件下脉动风对塔体结构响应的动力放大效应不同。进一步分析，在风向角从0°增大至60°时，不同模型塔体风振系数减小幅度相差不大。而风向角从60°增大至90°时，塔线体系模型风振系数降低速度明显大于无导线模型对应结果。因此可以得到，塔线耦合作用减弱了风向作用对塔体的动力放大效应，且在风向角为60°至90°时，此影响效果进一步加大。