初始渗流场对渣土场边坡降雨入渗特征及其稳定性的影响

李丞，蔡立明，张伟锋，侯建香，董凯，苏立君,2,3,4

(1.中国科学院 山地灾害与地表过程重点实验室；中国科学院、水利部成都山地灾害与环境研究所，成都 610041；2.中国科学院 青藏高原地球科学卓越创新中心，北京 100101；3.中国-巴基斯坦地球科学联合研究中心，巴基斯坦 伊斯兰堡；4.中国科学院大学，北京 100049；5.北京航天控制仪器研究所，北京 100854；6.深圳信息职业技术学院，广东 深圳 518127；7.深圳市城市公共安全技术研究院有限公司，广东 深圳518000)

随着城市化进程的加快，产生了以大量废土和废渣为主的余泥渣土，对城市固体废弃物的管理和城市规划提出了挑战[1]，而填埋是最常见的渣土处理方法[2]。对于渣土场边坡而言，其稳定性受填料性质、施工工艺、降雨、地下水位等影响[3-4]，在众多因素中，降雨入渗将导致渣土场边坡含水率增加、基质吸力降低和地下水位上升，这是渣土边坡变形与稳定性下降的主要原因之一[5-7]。

降雨作用下渣土场边坡的渗流特征和稳定性的研究主要集中在几个方面：1)降雨强度和初始含水率对渗滤液产量的影响[8-9]；2)降雨模式和降雨强度对边坡水分运移及其稳定性的影响[10-11]；3)降雨模式和降雨强度对填埋场覆盖层渗流特性的影响[12-13]；4)降雨强度对渣土场边坡变形破坏特征的影响[14-15]。以上成果对于理解渣土场边坡的水分运移规律和稳定性计算起到了关键的作用。然而，上述研究鲜有涉及初始渗流场对渣土场边坡降雨入渗机制的影响。值得注意的是，在常规边坡的研究中，学者们分析了初始渗流场对降雨作用下边坡渗流特征和稳定性的影响[16-18]。其中，唐栋等[17]研究了不同初始渗流条件对不同土体边坡稳定性的影响，结果表明，初始渗流条件对边坡安全系数影响很大，并建议将多年平均降雨量对应的稳态渗流场作为初始渗流条件。何忠明等[19]比较了4类初始渗流场对边坡降雨入渗过程的影响，发现初始渗流场分布形式对降雨过程中边坡表面孔隙水压力的影响较小，且初始基质吸力越大，受到降雨入渗的影响程度则越小。然而，由于填筑材料的差异性，渣土场边坡的降雨渗流特征和稳定性分析较常规边坡复杂[14,20-21]，因此，初始渗流场对渣土场边坡降雨入渗和稳定性计算的影响值得深入研究。

笔者以深圳市部九窝渣土场边坡为研究对象，结合室内土工试验及实际降雨资料，采用数值分析方法，在探讨不同初始渗流场和不同降雨强度对渣土场边坡的渗流特征影响的基础上，研究了渣土场边坡的安全系数变化规律。

1 计算原理

1.1 非饱和渗流原理

边坡降雨入渗过程可认为是典型的饱和-非饱和渗流过程，通常认为，在非饱和状态下达西定律依然适用，介质水力传导度是含水率的函数，Richards等[22]建立了土体中液体瞬时流动的二维控制方程

(1)

式中：hm为基质吸力水头，m；k(hm)为非饱和土渗透系数，m/s；C(hm)为比水容量，无量纲。

岩土体的渗透系数与土体体积含水率以及基质吸力相关，为了描述这三者之间的关系，通常需绘制土水特征曲线以及渗透系数曲线来说明。目前，确定土体渗透系数经常用到的方法是结合室内试验结果和经典公式[23]

(2)

kw=ks·

(3)

式中：ua为孔隙气压力，kPa；uw为孔隙水压力，kPa；θw为不同基质吸力条件下土体体积含水率，无量纲；θs为土体饱和体积含水率，无量纲；θr为残余体积含水率，无量纲；α为土体达到进气值时基质吸力的倒数，无量纲；n为孔隙尺寸分布参数，无量纲；ks为饱和渗透系数，m/s；kw为不同基质吸力条件下的渗透系数，m/s。

1.2 非饱和土强度理论

在考虑基质吸力的滑坡稳定性分析中，采用非饱和土抗剪强度理论对安全系数进行分析，它是莫尔-库仑模型的一个扩展模型

τ=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(4)

式中：c′为有效粘聚力，kPa；φ′为有效内摩擦角，(°)；σ为总法向应力，kPa；ua为孔隙气压力；uw为孔隙水压力，kPa；ua-uw为基质吸力，kPa；τ为非饱和土抗剪强度，kPa；φb为随基质吸力变化的内摩擦角，(°)。

2 有限元模型及计算方案

2.1 工程实例概况

选取深圳市部九窝人工渣土场边坡作为研究对象，依据压实度和施工工艺不同，可划分为3个区：渣土区(压实度为80%，坡比为1∶1.275)、填埋严控区(压实度为85%，坡比为1∶1.25)和坝体区(压实度为90%，坡比为1∶1.25)，图1为渣土场边坡2017年12月的平面图。研究场地属于亚热带季风气候区，年平均温度22 ℃，年平均降雨量1 900 mm，降水量集中在三月到九月。

图1 深圳市部九窝渣土场边坡平面图Fig. 1 Top view of municipal solid waste landfill in

2.2 边界条件及计算模型

根据工程地质调查确定图1中的AB断面为计算采用的剖面，剖面图如图2所示。采用理想弹塑性模型和Mohr-Coulomb屈服准则在Geo-studio中建立数值分析模型[24]，模型共划分13 232个节点和13 250个单元。在模型中设置监测截面1、2、3，每个截面的高度为8.8 m，其中，在监测截面1和2坡面处各有一个监测点，在监测截面3坡面处设置监测点3，在离监测点3的竖直方向4.4 m处设置监测点4，各监测截面和监测点用来监测边坡在降雨过程中的渗流特征，监测方案如图2所示。初始地下水位位于岩土分界面，地下水位线以上土体处于饱和-非饱和状态。在降雨渗流计算中，定义坡面为单位流量边界以模拟降雨入渗过程，同时，保证两侧和底部为不透水边界。

图2 模型剖面图和监测点布置Fig.2 Model section and layout of monitoring

根据室内土工试验所得结果，测得各岩土体的饱和渗透系数值和饱和体积含水率，并用式(2)和式(3)所示VG模型拟合得到岩土体非饱和渗透系数与基质吸力的关系曲线，如图3所示。此外，当土体的体积含水率达到其自身饱和体积含水率的90%时，则认为土体已经达到饱和状态[19]，因此，没有特别说明时，体积含水率大于或等于饱和含水率的90%的区域均视为饱和区范围，即暂态饱和区(Transient Saturated Zone，简称TSZ)。岩土体物理力学参数见表1。

图3 岩土体水力学参数Fig.3 Hydraulic parameters of rock and

表1 岩土体物理力学参数Table 1 Physical and mechanical parameters of rock and soil

2.3 计算方案

结合深圳地区区域气象条件，设计了如表2所示的3种工况。由于直接测定坡体内的初始基质吸力分布比较困难，而且费时费力[16]，为了研究初始渗流条件对边坡渗透特性和稳定性的影响，参考前人研究[16-19]，假设地下水位以上土体基质吸力呈线性增加，达到吸力上限后保持常数。假设坡体内基质吸力上限分别为-25、-50、-75 kPa，并通过微小降雨量形成稳态渗流达到上限值[25]，将稳态渗流形成的基质吸力作为初始渗流条件，如图4所示。3种工况在进行降雨入渗瞬态分析时均设置3种降雨强度q1、q2和q3，以此研究不同降雨强度下初始渗流场对边坡降雨入渗特征和稳定性的影响。

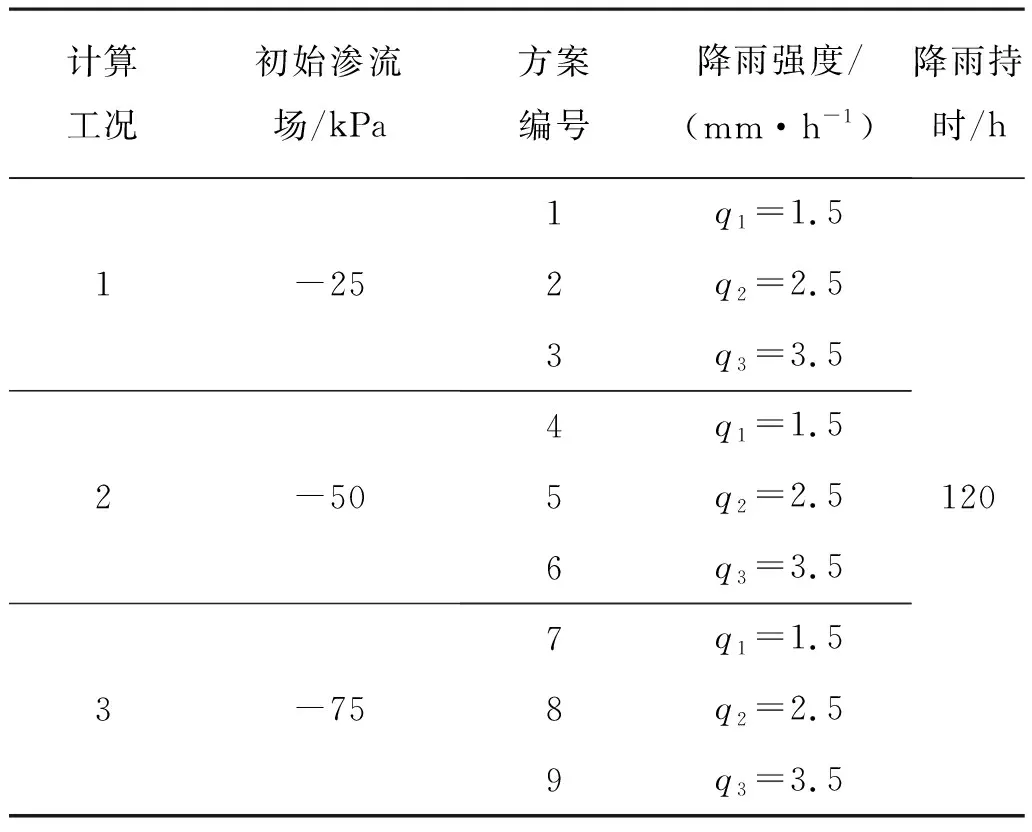
表2 计算方案Table 2 Calculation scheme

图4 边坡初始渗流场分布Fig.4 Initial seepage field distribution of

3 结果与分析

3.1 边坡监测点流速变化规律

当降雨强度为q1～q3(1.5～3.5 mm/h)和不同初始渗流场时，监测点1、2、3处Y方向流速随降雨持时的变化关系如图5所示。由图5可知，监测点1、2、3的流速均是先增大后减小，最后略大于降雨强度，且同一情况下，监测点2的流速最大，监测点3的流速次之，监测点1的流速最小；对于同一初始基质吸力和监测点，降雨强度越大，流速的峰值越大，且达到峰值的时间越短；对于同一降雨强度和监测点，初始基质吸力越大，流速的峰值越大，且达到峰值的时间越长。此外，当初始基质吸力为-25 kPa时，降雨强度越小，各监测点间流速的数值差距越小，而当初始基质吸力减小至-75 kPa后，各监测点间流速的数值差距越大。

3.2 边坡监测点暂态饱和区形成时间规律

当降雨强度为q1～q3(1.5～3.5 mm/h)和不同初始渗流场时，监测点1、2、3处的体积含水率随降雨持时的变化关系如图6所示。由图6可知，对于同一初始基质吸力和监测点，降雨强度越大，体积含水率上升速度越快，达到饱和的时间越短，降雨强度越小，暂态饱和区形成的时间越长，甚至不会出现暂态饱和区，以图6(a)中的监测点1为例，监测点1在q2和q3时达到饱和的时间分别为29、10.9 h，而在q1时没有达到饱和；对于同一降雨强度和监测点，初始基质吸力越大，体积含水率上升速度越慢，达到饱和的时间越长，以图6中的监测点1为例(降雨强度q3)，监测点1在初始基质吸力为-25、-50、-75 kPa时达到饱和的时间分别为10.9、20.2、25.5 h。

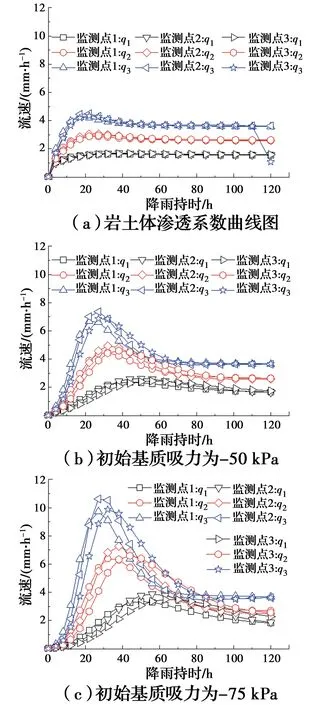
图5 监测点1、2和3的Y方向流速变化Fig.5 Velocity changes in Y direction at monitoring

图7为当降雨强度为q3时，不同深度监测点的体积含水率和Y方向流速的变化。由图7可知，斜坡表面监测点(监测点3)的流速与体积含水率变化要快于坡体内部的监测点(监测点4)，表明暂态饱和区从坡表向坡内扩展；对监测点3而言，体积含水率随着流速的增加而缓缓增大，当流速达到峰值时，体积含水率也达到绝对饱和(28%)，随后流速开始下降，体积含水率开始保持不变。值得注意的是，监测点3在120 h时的流速和体积含水率发生了突变(A点和B点)，这是由于降雨导致了地下水位大幅度上升，且地下水已经淹没了监测点3。

3.3 边坡暂态饱和区形成深度规律

当降雨强度在q1～q3(1.5～3.5 mm/h)和不同初始渗流场时，监测截面1、2、3处的暂态饱和区深度随降雨持时的变化关系如图8所示。由图8可知，对于同一初始基质吸力和监测截面，降雨强度越大，暂态饱和区深度越大；对于同一降雨强度和监测截面，初始基质吸力越小，入渗深度越大，截面处暂态饱和区出现的范围越大，体积含水率变化范围越小，体积含水率在同一位置增大的幅度也越大。此外，当降雨强度为q1时，截面1和2都没有产生暂态饱和区，截面3的暂态饱和区深度也较小，最大值仅为1.15 m，而当降雨强度为q3时，截面3的暂态饱和区深度最大值却达8.79 m，由此可见，降雨强度会显著影响边坡是否会出现暂态饱和区，而初始基质吸力则会对暂态饱和区深度的数值产生影响。

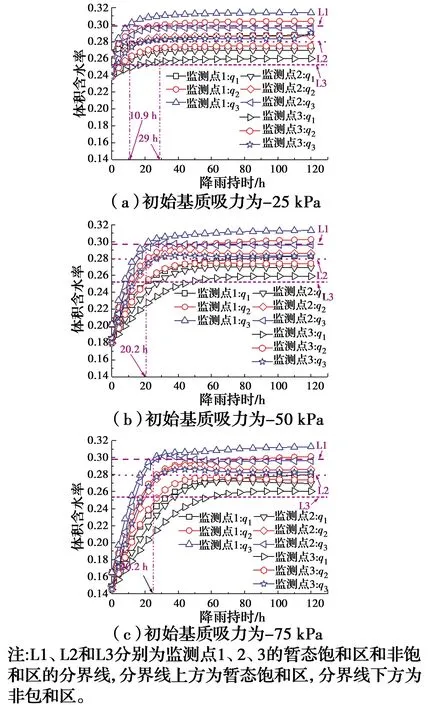
图6 监测点1、2和3的体积含水率变化Fig.6 Change of volumetric moisture content at monitoring points 1, 2 and

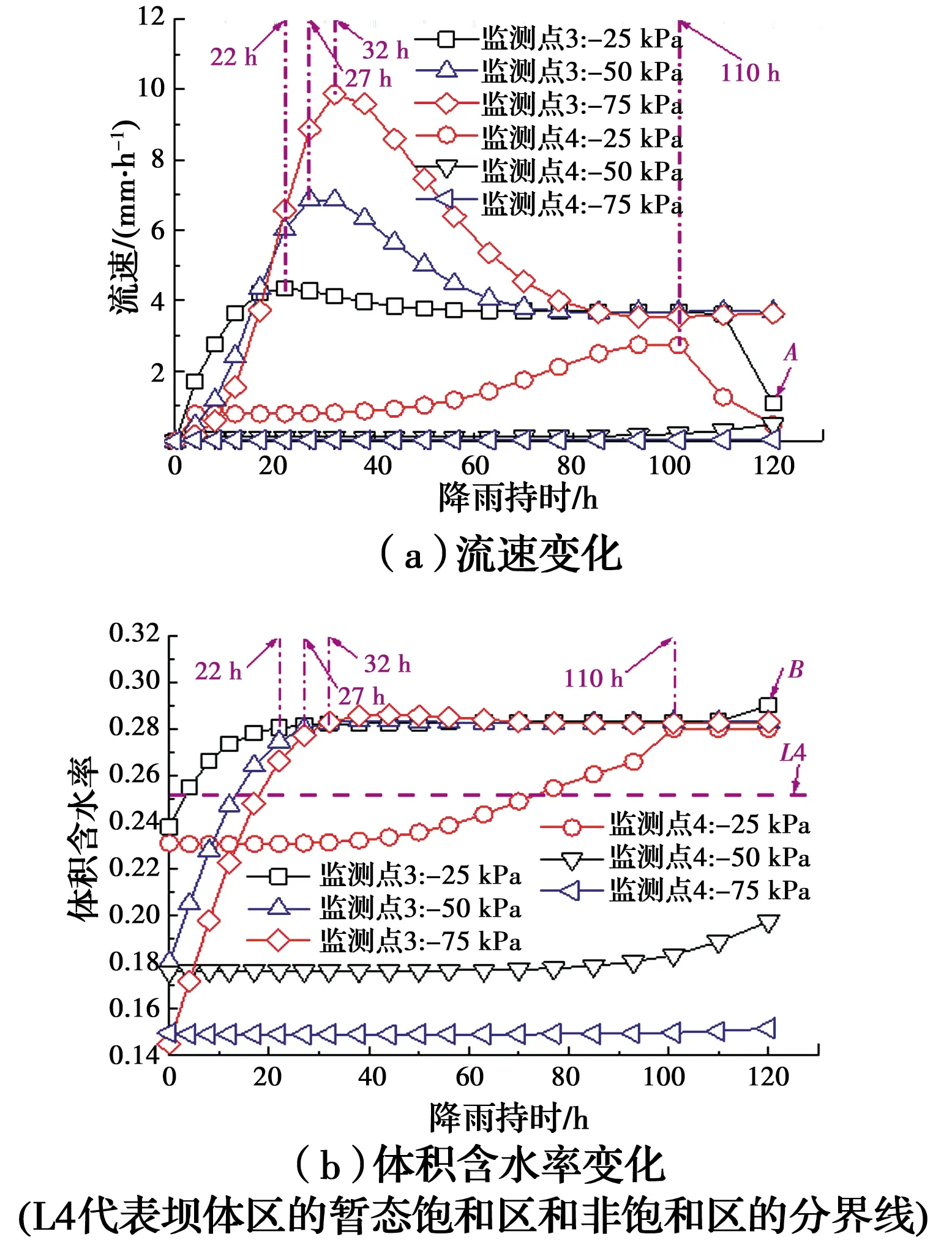
图7 监测点3和4的体积含水率与流速变化Fig.7 Volume moisture content and flow rate change of

图8 监测截面1、2和3的暂态饱和区深度变化Fig.8 Monitoring the depth variation of transient saturation zone at Sections 1, 2 and

3.4 边坡孔隙水压力变化规律

当降雨强度为q1～q3(1.5～3.5 mm/h)和不同初始渗流场时，监测点1、2、3处的孔隙水压力随降雨持时的变化关系如图9所示。由图9可知，随着降雨时间的持续，坡面孔隙水压力出现了升高的趋势。具体表现为：对于同一初始基质吸力和监测点处，降雨强度越大，入渗深度越大，孔隙水压力上升速率越快，降雨结束后的孔隙水压力也越小；对于同一降雨强度和监测点处，初始基质吸力较大的边坡孔隙水压力上升速率快于初始基质吸力较低的边坡，同时，坡面孔隙水压力升高速率整体上逐渐减小并趋于水平，就降雨持续时间内孔隙水压力的数值而言，初始渗流条件对各情况下降雨结束后的孔隙水压力的影响较小。由此可见，降雨强度会显著影响孔隙水压力增长的快慢，而初始基质吸力影响较小。

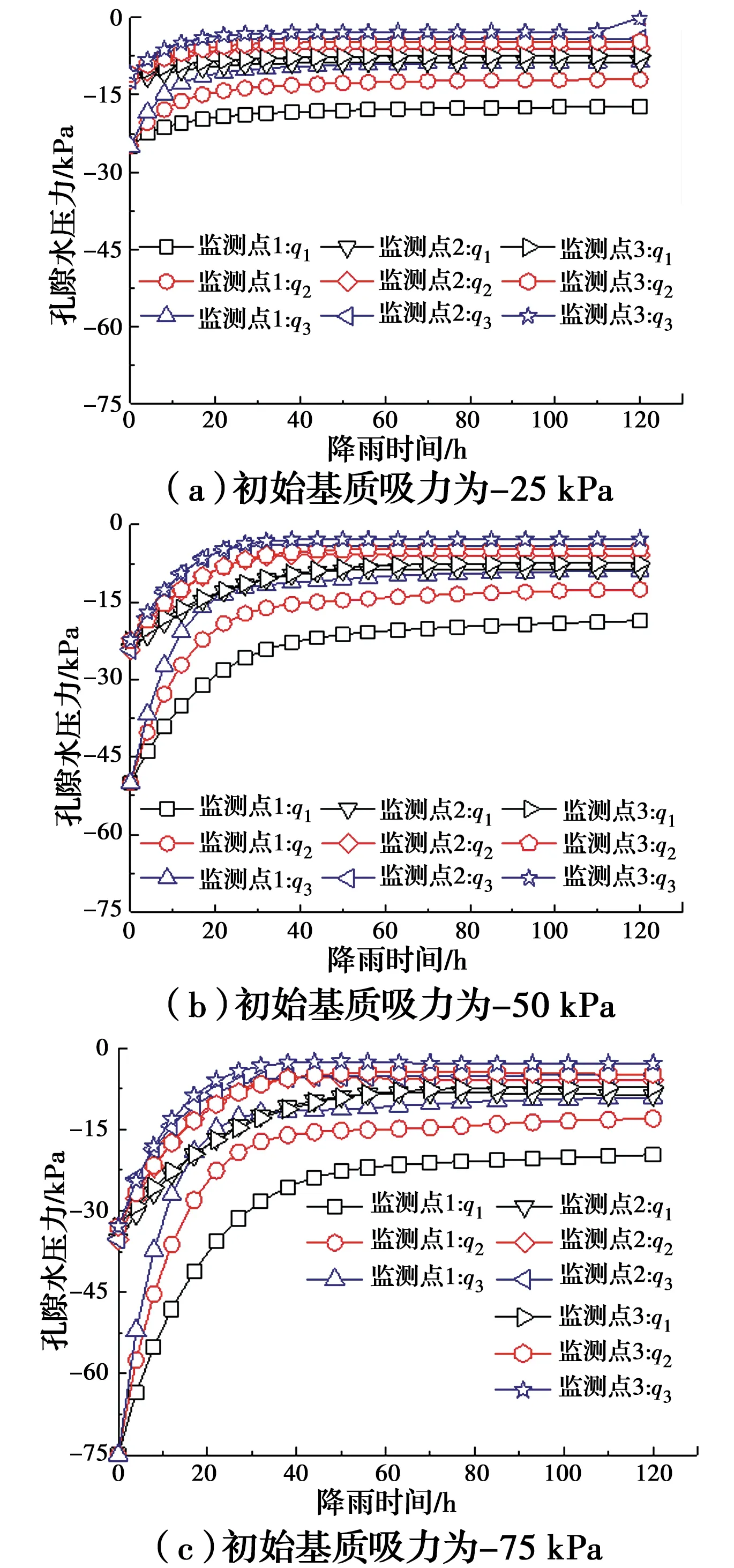
图9 降雨时间过程中孔隙水压力的分布Fig.9 Distribution of pore water pressure during rainfall

3.5 降雨条件下边坡稳定性分析

由前述可知，在不同初始渗流场和降雨强度的影响下，降雨过程中边坡的渗流特性和孔隙水压力变化规律有所差异，因此，针对图2所示边坡，探讨其边坡稳定性的变化规律。当不考虑降雨时，对边坡初始安全系数进行计算，最危险滑动面通过SLOPE/W程序自动搜索确定，采用有限单元应力法求解安全系数，以初始基质吸力为-25 kPa时为例，边坡安全系数为1.623，最危险滑动面如图10所示。由图10可知，边坡最危险滑动面同时位于坝体区和填埋严控区内，考虑到坝体溃决的可能性，为简单起见，在降雨持续过程中，分析坝体区内(即监测截面3)的暂态饱和区厚度的变化规律对边坡稳定性的影响。

图10 初始基质吸力为-25 kPa时的最危险滑动面Fig.10 The most dangerous sliding surface when the initial

降雨强度为q1～q3(1.5～3.5 mm/h)和不同初始渗流场时的边坡安全系数变化如图11所示。由图11可知，暂态饱和区厚度对边坡稳定性影响显著，且边坡初始基质吸力为-50、-75 kPa时，边坡安全系数下降趋势和暂态饱和区厚度增加趋势均呈线性。此外，由图11(a)可知，当降雨强度为q1时，边坡没有产生暂态饱和区，且初始基质吸力为-25 kPa时的安全系数下降速率最大；由图11(b)可知，

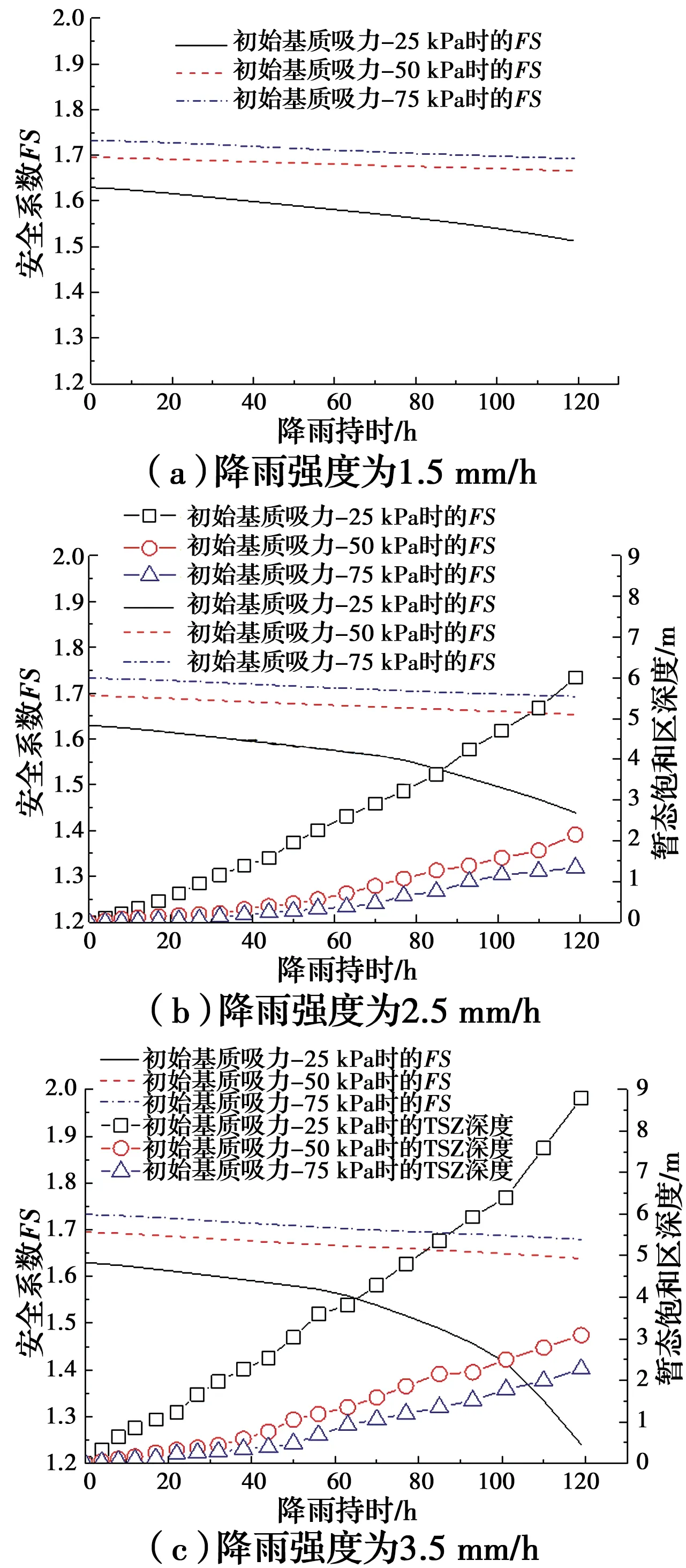
图11 暂态饱和区厚度对边坡安全系数的影响Fig.11 Influence of transient saturated zone thickness

降雨强度为q2时暂态饱和区的最大厚度分别为6.00、2.15、1.34 m，降雨结束后，边坡安全系数分别为1.439、1.653、1.693；由图11(c)可知，当降雨强度为q3时，初始基质吸力为-25 kPa的边坡安全系数下降呈非线性趋势，最小值为1.241，相应地，其暂态饱和区厚度增加也呈非线性趋势，最大值为8.79 m。综合图11可知，在相同初始基质吸力条件下，暂态饱和区厚度为8.79 m时的安全系数与没有暂态饱和区时的安全系数最大相差0.272，降幅约21.91%；在相同降雨强度下，暂态饱和区厚度为8.79 m时的安全系数与暂态饱和区厚度为2.27 m时的安全系数最大相差0.429，降幅约35.37%。

当初始基质吸力为-25 kPa时，边坡初始安全系数为1.623，具备很好的安全储备，而经历120 h的强降雨后(q3=3.5 mm/h)，安全系数只有1.241，且结合监测点暂态饱和区形成时间规律可知，在降雨作用下，坝体区的地下水位大幅度上升，并已达到坝体区坡顶。目前，中国关于渣土场边坡相关的设计规范还未成熟，若借鉴碾压土石坝的设计标准：坝坡正常条件下的最小安全系数为1.25(简化毕晓普法)，非正常运用条件Ⅰ时的最小安全系数为1.15(简化毕晓普法)[26]。由此可知，在初始基质吸力更小或遭遇强度更大的降雨时，若没有相应的工程措施，渣土场边坡具有失稳风险。

4 讨论

基于非饱和渗流原理和非饱和土强度理论建立数值模型，探讨了初始渗流场和降雨强度对渣土场边坡的降雨入渗特征及稳定性的影响，得到的结论为渣土场的长期运营及排水防渗工作提供了参考依据。

一般而言，在数值模拟研究中，常规边坡多为单级边坡，且构成物质单一，其在降雨作用下的渗流特征和稳定性分析已经比较明确。然而，渣土场边坡基本为多级边坡，其填筑过程分阶段、分区域进行，这使得不同区域的岩土体力学参数存在差异，从而改变了渣土场边坡的渗流特征，并显著影响边坡稳定性。具体体现为：需要综合分析渣土场边坡的整体稳定性和渣及其各自区域内单极边坡的稳定性。从文献[15]可知，在降雨作用下，渣土场边坡下部的安全系数要小于其上部和中部的安全系数，为简单起见，只计算了渣土场边坡下部的安全系数，分析了渣土场边坡发生“溃坝”的失稳隐患。综合分析渣土场边坡的多种失效模式将是下一步研究的工作重点。

另一方面，考虑初始渗流场影响的渣土场边坡降雨入渗过程分析是从数值模拟的角度进行的，一定程度上可以为实际场地的相关分析提供理论支撑，在后续研究中应通过现场监测和模型试验等手段对结果进行检验与修正。

5 结论

1)初始渗流场和降雨强度对渣土场边坡的降雨入渗特征有显著影响。初始基质吸力越大，Y方向流速的峰值越大，达到峰值的时间越长，且体积含水率上升速度越慢，达到饱和的时间越长。降雨强度越大，Y方向流速的峰值越大，达到峰值的时间越短，且体积含水率上升速度越快，达到饱和的时间越短。

2)渣土场边坡暂态饱和区的渗流特征可描述为：坝体区坡面以下土体迅速饱和，暂态饱和区范围由坝体区坡脚附近加速向上部土体扩散，并逐渐覆盖整个坝体区，同时由坝体区向填埋严控区漫延。

3)初始基质吸力较大的边坡孔隙水压力上升速率快于初始基质吸力较低的边坡。渣土区的孔隙水压力上升速率最快，填埋严控区和坝体区的孔隙水压力上升速率差别不大。降雨强度会显著影响孔隙水压力增长的快慢，而初始基质吸力影响较小。

4)初始渗流场对渣土场边坡安全系数有显著影响。边坡安全系数与暂态饱和区厚度的关系为负相关。在初始基质吸力为-25 kPa时，经历了120 h降雨后(3.5 mm/h)，渣土场边坡安全系数下降明显，具有一定的失稳风险，因此，在渣土场进行填筑的过程中，为确保坝坡长期稳定，应充分考虑区域气象条件对渣土场运营期稳定性的影响，做好渣土场边坡排水和防渗设施，防止发生坝体区溃坝。