粘弹性悬臂输流管道在激励力下的稳态响应分析

刘 颖,郭长青

(南华大学 土木工程学院,湖南 衡阳 421001)

0 引 言

输流管道广泛应用于航空、水利、核能、石油和海洋等领域，因其广泛的应用范围使得与之相关的流固耦合振动问题在近一个世纪以来受到了广泛的关注和研究[1-14]。现阶段关于这类问题的研究主要分为研究方向的选择和求解方法的寻求。任建亭等[7]从五个研究方向简述了近年来输流管道流固耦合振动的研究进展，并提出了进一步的研究方向以及采用的相应对策；初飞雪[9]根据Hamilton原理采用直接解法解得了输流管道自由振动的固有频率、临界流速和临界压力的解析解表达式；易浩然等[11]基于哈密顿原理建立了含集中质量悬臂输流管的非线性动力学理论模型，研究了集中质量对悬臂输流管稳定性和振动模态特性的影响规律；周坤等[12]基于绝对节点坐标法推导出由不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程，并通过数值求解的方式对周期性输流管道的稳定性和非线性动力学行为进行了研究；许锋等[10]通过传递矩阵法结合边界条件求出了输流管道模态函数的频率特征值；文献[3,5-6,10]使用Galerkin法研究了输流管道系统的固有特性；张挺等[13]采用广义有限差分法和Houbolt法分别对空间和时间上的偏微分项进行离散，建立高阶精度的无网格法数值模式，分析比对了两端简支、两端简支和一端固支一端简支下输流直管的振动响应特性；谌冉曦等[14]运用ANSYS Workbench软件分析了弯曲半径对所受流体压力以及内部流速分布的影响；文献[1,4]运用Green函数法求得激励力作用下有阻尼梁的动态响应表达式；H.B.Wen等[2]应用Green函数法研究了输流管道系统的固有特性；孙志礼等[8]研究了两端支承式输流管路的强迫振动分析，采用Green函数法求得输流管道的一般挠度表达式。本文在已有研究的基础[1-2,4,8]上，对粘弹性悬臂输流管道在激励力下的稳态响应进行研究，考虑了激励点位置、粘弹性系数、质量比及流速对悬臂输流管道稳态响应的影响。

1 运动微分方程

如图1所示，悬臂输流管道系统管道内流体以恒定流速流动。

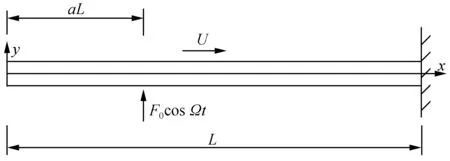
图1 悬臂输流管道受激励力动力学模型Fig.1 Excited dynamic model of cantilever pipeline

管道采用Bernoulli-Euler梁模型，位置x处、t时刻的挠度为w(x,t),其运动微分方程为：

(1)

式中：EI为管道抗弯刚度，E*为粘弹性系数，w为管道横向位移，L为管道长度，M为单位长度管道内流体的质量，m为单位长度管道质量，U为管道内流体流速，F0为激励力幅值，δ(·)为狄拉克函数，Ω为激励频率。

引入以下无量纲量：

(2)

将式(1)无量纲化为：

(3)

2 运动微分方程的求解方法

假设方程(3)的解为以下形式：

W(ξ,τ)=X(ξ)eiωτ

(4)

将式(4)代入式(3)得：

ω2X=fδ(ξ-a)

(5)

对式(5)进行Laplace变换：

(6)

解得：

(7)

其中：

(8)

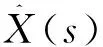
(9)

通过文献[2,4]中的方法可得到：

(10)

其中：

(11)

式(10)中u(x-a)为单位阶跃函数

运用式(10)，对式(7)进行Laplace逆变换可以得到X(ξ)的Green函数形式解：

(12)

其中：

(13)

为了得到管道的振型函数；对式(12)进行求导:

(14)

在式(12)、式(14)中令ξ=1，可以得到左端(ξ=0处)和右端(ξ=1处)边界条件的关系式：

(15)

3 悬臂管道的稳态响应解

图1所示悬臂梁的边界条件为：

(16)

将式(16)代入式(15)，其前两式化为

(17)

解得：

(18)

(19)

将式(18)、式(19)代入式(12)得输流管道振型函数的Green函数解：

(20)

4 计算结果

4.1 计算方法的验证

根据推导过程可知，Green函数所得解式为封闭形式解，它比模态叠加法所得的解更能体现系统的物理特性。为了验证此方法的正确性，我们去掉激励力，并设粘弹性系数为零，通过式(15)得到悬臂输流管道的频率方程和模态函数，经计算其结果和文献[2]吻合。

4.2 计算结果及分析

图2给出了四种不同激励点位置下自由端挠度X(0)的反应谱，可以看出：随着激励点位置由自由端向固定端不断靠近，自由端挠度X(0)的一阶共振幅值会不断降低，但其下降幅度会逐渐减小。

图3、图4给出了八种不同粘弹性系数下自由端挠度X(0)的反应谱，从图3可以看出：随着粘弹性系数的增加，X(0)的一阶共振幅值会先增大后减小，同时其一阶共振频率会一直降低；从图4可以看出：随着粘弹性系数的继续增加，系统一阶共振频率会继续降低，系统二阶共振幅值开始逐渐增大，系统一阶和二阶频率开始逐渐融合，其共振幅值也不断增大。

(β=0.2,α=0.1,ν=10,f=10)图2 不同激励点位置下的反应谱Fig.2 Response spectrum under different positions of excitation

(α=0～0.2,β=0.2,a=0.25,ν=10,f=10)图3 不同粘弹性系数下的反应谱Fig.3 Response spectrum under different viscoelastic coefficients

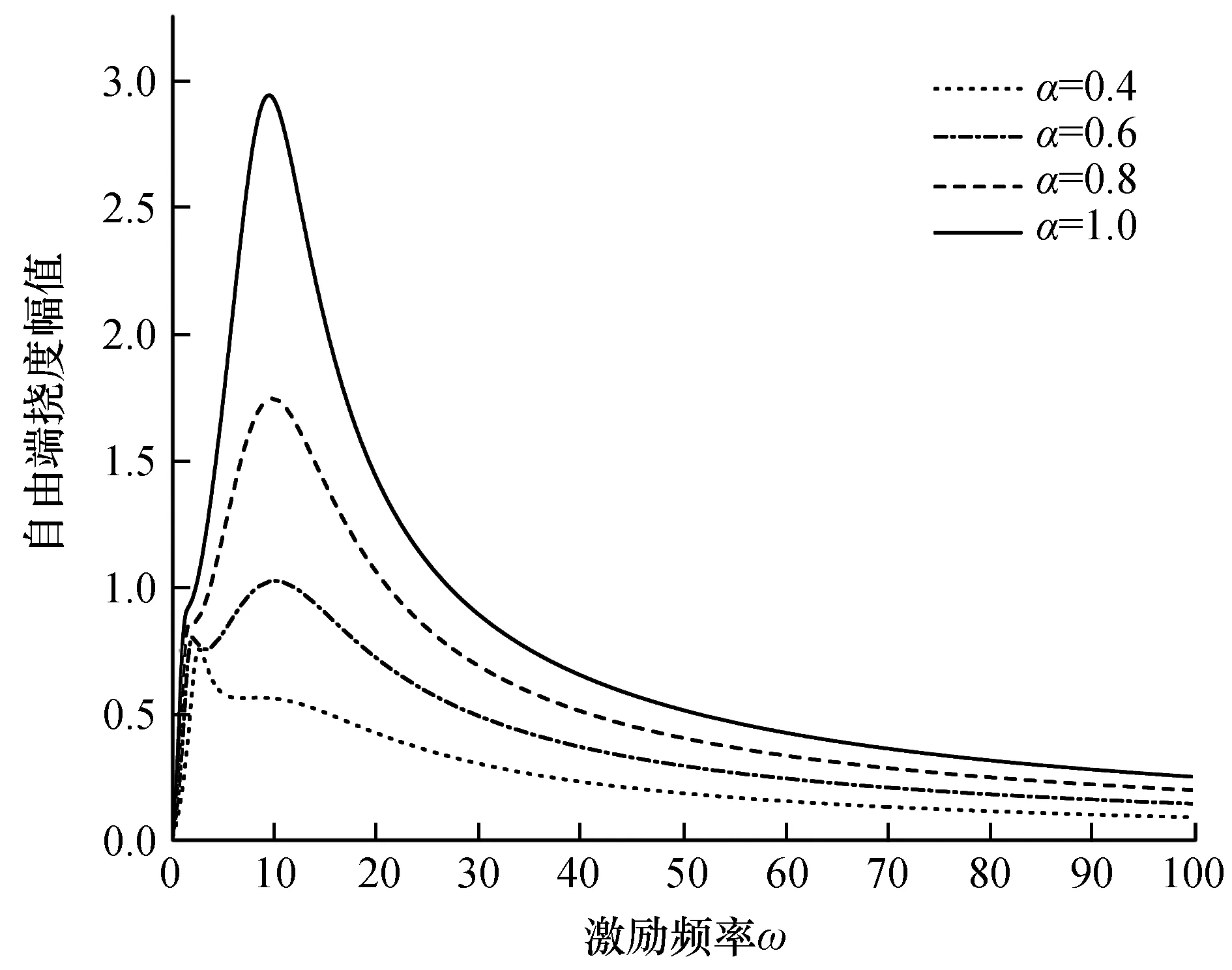
(α=0.4～1,β=0.2,a=0.25,ν=10,f=10)图4 不同粘弹性系数下的反应谱Fig.4 Response spectrum under different viscoelastic coefficients

图5给出了四种不同质量比β下自由端挠度X(0)的反应谱，可以看出：随着质量比的增加，X(0)的一阶共振幅值会先增大后减小，其一阶共振频率也会先小幅升高后小幅降低。

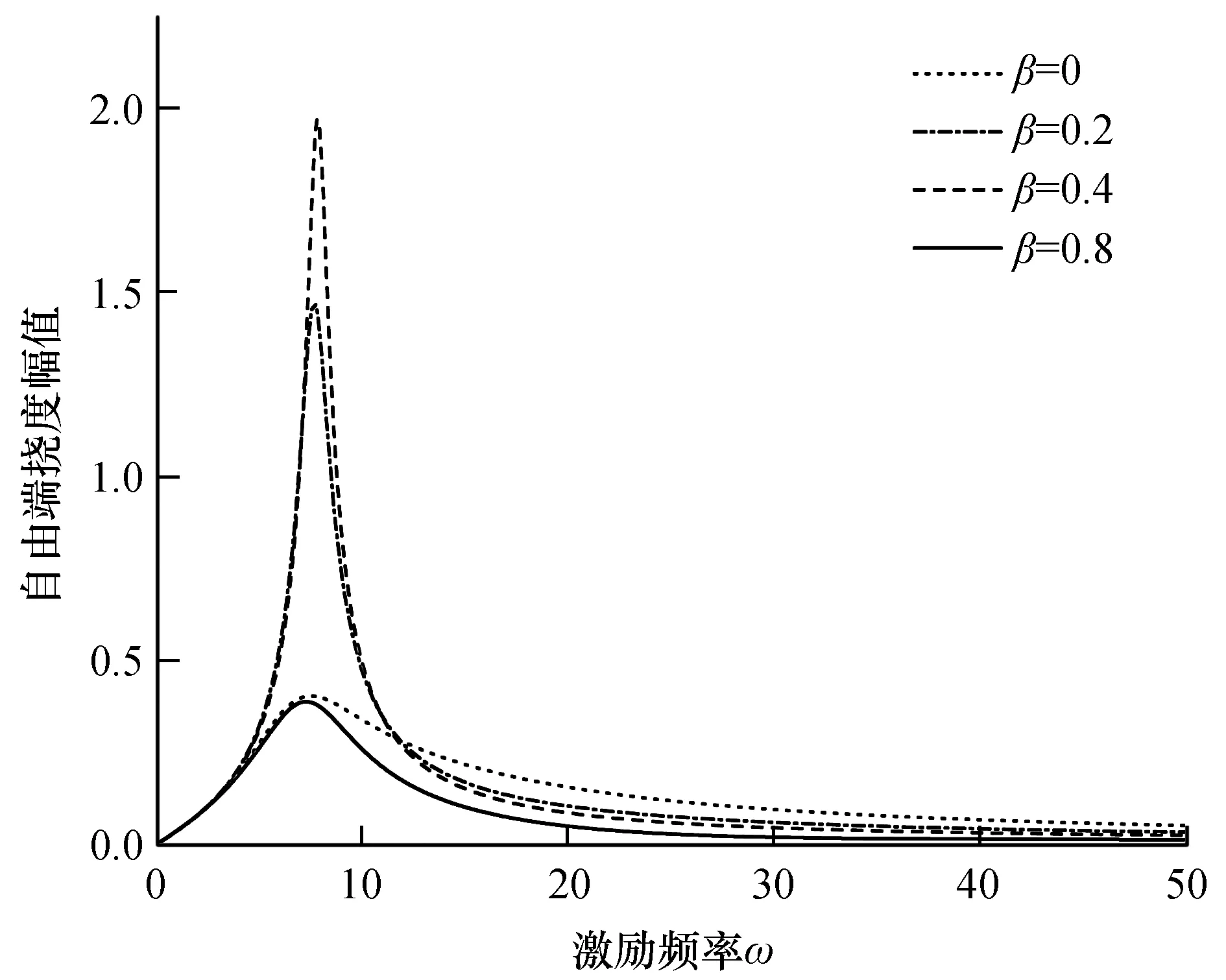
(ν=10,α=0.1,a=0.25,f=10)图5 不同质量比下的反应谱Fig.5 Response spectrum under different mass ratios

图6给出了四种不同正流速(从自由端流向固定端)下自由端挠度X(0)的反应谱，可以看出：随着流速的增加，X(0)的一阶共振频率会先增大后减少，同时其一阶共振幅值也会先降低后升高。

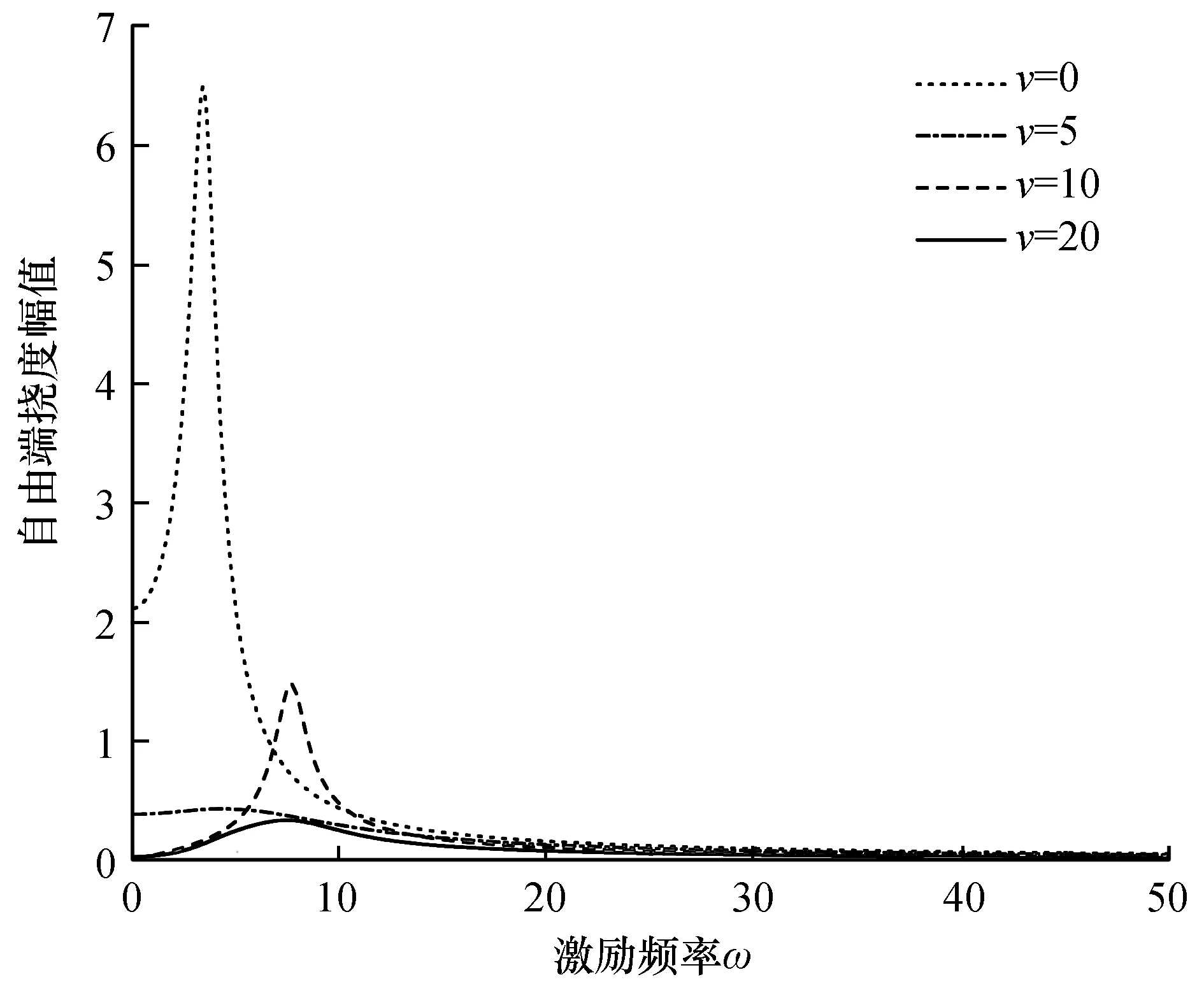
(ν=0～20,β=0.2,α=0.1,a=0.25,f=10)图6 不同正流速下的反应谱Fig.6 Response spectrum under different positive flow rates

图7给出了四种不同负流速(从固定端流向自由端)下自由端挠度X(0)的反应谱，可以看出：随着负流速绝对值的增加，X(0)的一阶共振频率会先增大后减小，同时其一阶共振幅值也会先降低后升高。

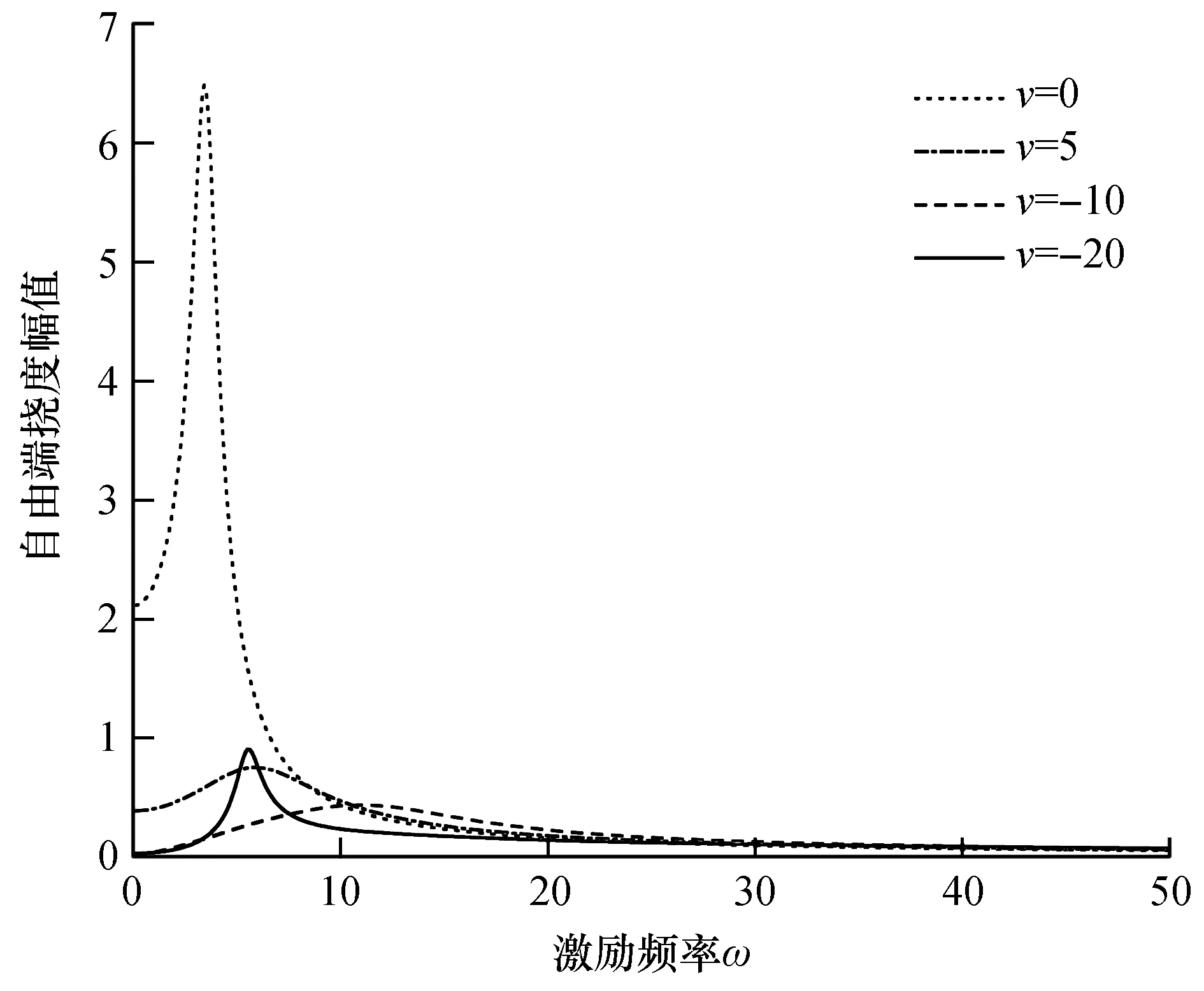
(ν=-20～0,β=0.2,α=0.1,a=0.25,f=10)图7 不同负流速下的反应谱Fig.7 Response spectrum under different negative flow rates

5 结 论

本文运用Green函数法推导了悬臂输流管道的强迫振动微分方程，并得到系统稳态响应的解析解，其解比模态叠加法更能体现模态的物理特性。本文在推导的基础上研究分析了不同参数对系统稳态响应的影响，得到以下结论：

1)激励点位置离自由端越远，其对自由端共振幅值的影响越小。

2)随着粘弹性系数的增加，系统一阶共振频率会持续降低，当粘弹性系数增加到一定程度后，系统一阶二阶共振频率会开始逐渐融合。

3)质量比对系统一阶共振频率无明显影响，质量比对自由端一阶共振幅值影响较大。

4)流速对系统一阶共振频率、一阶共振幅值的影响无简单的规律性。