思易错之源悟纠错之道

2021-03-12文施长燕

初中生世界 2021年11期

关键词：平方根错因分式

文施长燕

“数与式”是初中数学的核心内容之一，它融合在诸多的知识之中。“数与式”既是重点知识，也是同学们易错的内容。为了让同学们能更好地规避错误，掌握所学，下面将“数与式”中的易错点进行整理，并结合易错题型让大家思考易错的源头，感悟纠错之道。

一、概念本质要心中有数

易错点1：无理数的概念理解不到位。

【错解】在所列实数中，无理数有 9，这4个。

故答案为4。

【错因分析】本题考查的是无理数的概念，错误的主要原因是没有真正理解无理数的概念，只看形式，而没有化简后再判断。无理数的常见类型有：①根号型，如等开方开不尽的数；②定义型，如1.010010001…（相邻两个1 之间依次多一个0）等；③含“π”型，如π+2 等。而且在判断之前要先化简，再结合无理数的常见类型去判断。

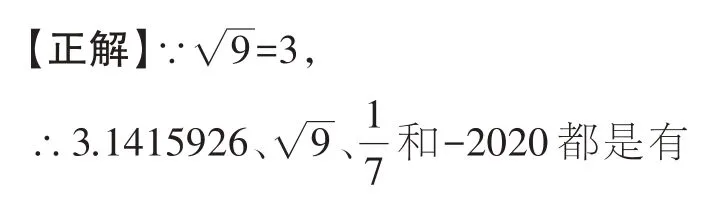
【错解】B。

【错因分析】本题考查的是倒数的概念，乘积为1的两个数互为倒数。但有些同学对倒数的概念把握不到位，易把倒数与相反数的概念混淆。绝对值相等、符号相反的两个数互为相反数。有的同学误认为-7的倒数是7，而非根据倒数的概念，用1去除以这个数来得到这个数的倒数。

【正解】根据倒数的定义，-7 的倒数是故选C。

易错点3：平方根与算术平方根的区别。

例3（2020•江苏南京）3 的平方根是（）。

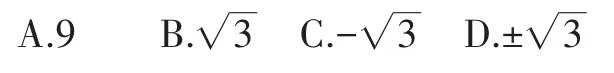
【错解】B。

【错因分析】本题考查的是平方根，但有同学往往会错选这个数的算术平方根。正数a 的平方根为是正负两个值，而其中正值是这个正数的算术平方根。

【正解】∵（± 3）2=3，∴3 的平方根是故选D。

二、解决问题要挖掘条件

易错点4：实数的大小比较。

例4 （2020•山东临沂）下列温度比-2℃低的是________。

A.-3℃ B.-1℃ C.1℃ D.3℃

【错解】B。

【错因分析】本题考查的是实数的大小比较，做错的原因往往是没有抓住两个实数如何比较大小的本质。任意两个实数比较大小要遵循：（1）在数轴上表示的两点，右边的点表示的数比左边的点表示的数大；（2）正数大于0，负数小于0，正数大于负数；（3）两个正数中，绝对值大的数大；（4）两个负数中，绝对值大的反而小。

【正解】根据两个负数，绝对值大的反而小可知。故选A。

易错点5：代数式有意义。

【错解】由2x-6≥0，可得x≥3。

【错因分析】本题考查的是二次根式和分式有意义的条件，关键是要掌握：（1）分式分母不为0；（2）被开方数是非负数。而在解决本题的过程中，有的同学只考虑了被开方数是非负数，而忽略了分母不为0。本题的被开方数还在分母上，因考虑不周全而导致求取值范围时出错。

∴x的取值范围是x＞3。

故答案为x＞3。

易错点6：分式的值为0 时，易忽视分母不能为0。

【错解】由 |x|-1=0，解得x=±1。故选C。

【错因分析】本题考查的是分式的值为0。分式的值为0的条件应是满足分子为0 且分母不为0。本题之所以解错，是因为只考虑到分子为0，即 ||x -1=0，而忽视了分式有意义的条件：分母不为0，即x+1≠0。

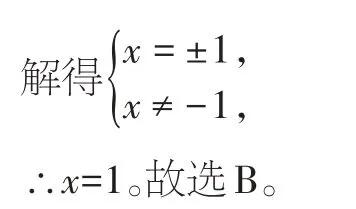
三、综合运算要步步为营

易错点7：运算时要把好符号关。

【错因分析】本题考查的是实数的运算，要正确进行实数的运算，就要掌握好与实数有关的概念、性质，灵活地运用各种运算律，关键是把好符号关。如遇到去绝对值问题，就要思考绝对值里的是正数还是负数。正数的绝对值等于它本身，负数的绝对值等于它的相反数。本题出错是因为去绝对值时，未处理好符号问题，同时求（-1）2020时，符号也出现问题，导致出现计算错误。

易错点8：分式运算要综合考虑。

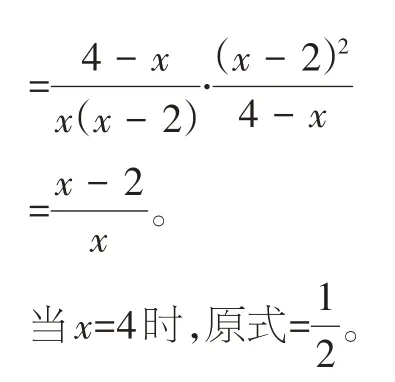
【错因分析】本题考查的是分式的运算。进行分式的运算时，要综合考虑：①运算法则和符号的变化；②分子或分母是多项式时，要分解因式且要分解到不能分解为止；③结果应化为最简分式。本题出错的原因是在取值时没有考虑“分母不为0”，即x≠0 和x-2≠0，同时忽视了除数不能为0的条件，即4-x≠0。故x≠0，x≠2，x≠4。