竖向荷载下砖石古塔的损伤性能
2021-03-11卢俊龙李传立韩鑫王振山
卢俊龙 李传立 韩鑫 王振山

摘 要:以玄奘塔首層为原结构,分别采用原砖、1/4和1/8模型砖制作了3个1/8缩尺结构模型,进行受压试验,观测加载过程中结构裂缝发展特征,测试了结构荷载、位移及应变;并通过数值模拟,对比了3个模型受力及破坏形式,分析了古砖塔的受压破坏机理和损伤变化。研究结果表明:砖塔受压破坏过程包含沿灰缝开裂、裂缝扩展和延伸、裂缝贯通破坏3个阶段;塔体破坏始于四角顶部,随荷载增加逐渐向下扩展并贯通,形成小截面砖柱,砖柱失稳导致结构破坏;塔壁沿平面内及平面外产生水平向变形,部分砖块开裂,因砖块尺寸不同导致模型的初始损伤及刚度不同,开裂荷载和极限承载能力随砌块尺寸减小而降低,应变随块体尺寸减小而增大,并根据模型的整体变形和局部块体变形特点,分析古塔的受压破坏机制,计算出古塔受压损伤演化趋势。
关键词:砖石古塔;力学性能;破坏模式;破坏机制;损伤演化
1 Introduction
Masonry pagodas were mainly constructed in China during the Tang Dynasty (A.D. 689 to 907). They are usually considered ancient high-rise buildings, among which the famous pagodas in China include the 84 m high Kaiyuan Temple pagoda located in Dingzhou City, Hebei Province and the 87 m high Chongwen pagoda in Jingyang County, Shaanxi Province. The ancient masonry pagodas were constructed of brick or stone blocks, with glutinous rice mortar or loess mud. Because of low mortar strength, the structures easily crack under long periods of high pressure, and the interiors become damaged. The stress results in the masonry pagodas being weakened in their bearing capacity or even in their collapse. Therefore, for the safety assessment of ancient pagoda structures, it is essential to analyze the process by which the masonry gets damaged under compression.
In the study of the compressive strength of brick masonry, Shi et al.[1] explored the effect of the variation of the ratio of height to thickness. They performed uniaxial, biaxial, and triaxial tests on clay brick, mortar, and masonry specimens and analyzed the failure criteria of masonry prisms. Several scholars have studied the mechanical properties of various types of masonry in terms of the mechanical properties, the strength and form of the masonry mortar, and the change in block form[2-5]. Useful application indices, which provide valuable references for the calculation and numerical simulation of masonry bearing capacity, have been presented in the literature[6-11]. The constitutive relationship of masonry is derived to analyze the variation of the stress-strain relationship for the intuitive description of the compressive strength, which has significant value for theoretical research and practical applications[12-15]. Currently, the established constitutive relationship of masonry is principally based on the relationship during the experimental process, and two types of curve forms are identified, namely, the ascending type and the full curve type[16-18]. Wang et al.[19] presented a novel perspective for investigating the failure process of masonry under pressure, based on the damage mechanics and elastic brittleness theory, and simulated the damage and cracking stages of masonry structures under loading. Yang et al.[20-22] introduced damage mechanics in the analysis of the pressure failure of masonry under uniaxial pressure.
In summary, studies concerning the compressive strength of masonry structures mostly analyzed the effect of masonry materials and masonry block types based on the experimental results. Owing to the low-strength masonry mortar and high pressure stress at the bottom of the pagoda, local damage occurs in cylindrical blocks. Compared with ordinary masonry structures, ancient pagoda masonry has unique characteristics in terms of low strength in masonry and bond form. Therefore, it is important to develop a model of ancient brick pagodas for testing the compressive strength and analyzing the failure mode and failure mechanism. The model can provide reliable references for the safety assessment of ancient brick pagodas.
Based on the micromechanical damage model of masonry, taking the first story of the Xuanzang pagoda located in Xingjiao Temple as the prototype, three structural models constructed with blocks of different sizes were tested. The basic failure mode and characteristics of the ancient masonry pagoda were determined from compression test results, and the dependence of the initial defect rate on the compression damage of the pagoda was obtained. The stress-strain relationship of the block and the compression damage curve of the pagoda were determined, providing the basis for the safety evaluation of the ancient masonry pagodas.
In this study, the compressive strength of the bottom structure of ancient masonry pagodas is investigated. Based on the damage theory, the pressure test results show the failure mechanism and the stress-strain relationship for brick models of masonry pagodas.
2 Materials and methods
2.1 Pressure test
2.1.1 Test model
The Xuanzang pagoda of Xingjiao Temple selected as the prototype structure is located in Xi'an City, Shaanxi Province, China. The pagoda is the resting place of the Buddhist relics of Master Xuanzang of the Tang Dynasty, and is square in plan. There is a room on the first floor and a stable structure above the second floor. A five-floor building, the pagoda body gets progressively narrower with each floor. The pagoda has a height of 21 m and a bottom edge of 5.2 m. The Xuanzang pagoda, shown in Fig.1, was among the first group of key cultural relics selected for protection in China in 1961.
Taking the first story of the Xuanzang pagoda as the prototype, a model scaled to 1/8 size was designed and constructed. The model has a quadrilateral shape with a side length of 0.7 m. The detailed design size is shown in Fig.1.
Abandoned bricks gathered from old houses demolished in the 1980s, and aged about 40 years with dimensions of 240 mm×115 mm×53 mm characterized by their regular appearance and favorable quality were used in the models. As shown in Fig.2 (a), raw bricks were cut using the cutting machine to produce the model brick with ratios of 1/4 and 1/8. The size of the model brick at a scale of 1/4 was 115 mm×53 mm×53 mm, and the size of the brick scaled at 1/8 was 115 mm×53 mm×26 mm. To draw a comparative analysis of the effect of initial defects caused by the mortar joints on the failure modes and bearing capacity, three models were generated in this test, which were original bricks, 1/4 bricks, and 1/8 bricks. Model 1 was made of original bricks, Model 2 was made of 1/4 scaled bricks, Model 3 was made of 1/8 scaled bricks. The water-lime ratio of the masonry mortar was 0.8, and the concentration of glutinous rice paste was 5% (glutinous rice (g): water (g)=0.05:1). The blocks are shown in Fig.2 (b). As shown in Fig.2 (c), the model was built on a 700 mm×700 mm steel plate with a mortal joint size of 5 mm by the same skilled worker. The constructed specimen model is shown in Fig.2 (d).
2.1.2 Test program
A 5 000 kN electro-hydraulic servo press was employed for the model test. Preloading was performed based on the displacement-loading mode to eliminate the assembling gap between the sand cushion and the bottom plate. A 10 kN preloading force was applied to test the displacement gauge and foil gauge performance during loading. When the value in the displacement gauge started to increase slowly with the loading, the preloading was stopped. The loading was applied at a constant speed of 0.15 mm/min and was stopped when instability occurred. During the test, the behavior was noted, and the displacement meter readings at different stages were read and recorded.
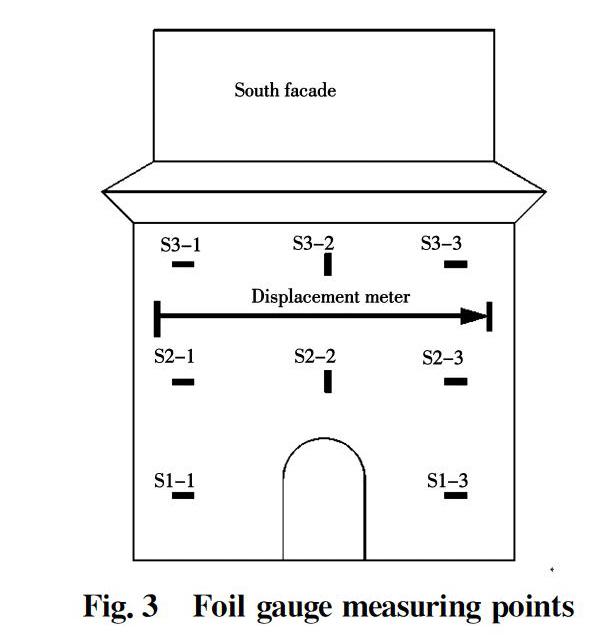
A vertical displacement meter was positioned in the eastern and northern facades at a distance of 420 mm. Similarly, a horizontal displacement meter was placed in the southern and western facades at 530 mm, and a horizontal displacement meter was set in the western and northern facades. Horizontal and vertical resistance foil gauges were fixed on the surfaces of the upper (about 5 cm from the top (S3-1, S3-2, S3-3)), middle (about 30 cm from the top (S2-1, S2-2, S2-3)), and lower (about 5 cm from the bottom (S1-1, S1-2, S1-3)) bricks at the corners of the southern facade, as shown in Fig.3.
2.2 Theoretical damage analysis
Ancient pagoda masonry mostly consists of glutinous rice mortar and clay mortar with low bonding strength, and cracks in masonry usually occur along the masonry joints under the action of external forces. Based on the analysis of the pressure and tension deformation characteristics of the brick masonry walls or column, the overall stress form of the model, the failure of the ancient pagoda under pressure can be simplified to the meso-failure form illustrated in Fig.4. The model is divided into cylinders with the area equal to Si,the height equal to the model height, where Si is the equivalent area decided by the number of cylinders. Respectively, the small cylinders are connected through springs to illustrate the tension forms of blocks (Fig.4).
During the early stages of loading, the stress-strain curve is expressed as a straight-line relationship with a decreasing tensile stress, and it is assumed that there is no damage in the springs, and no failure occurs in the cylinders. With the increase in load, the springs begin to break and internal micro cracks appear while buckling starts in the upper column, which is expressed as the non-linear growth mode of the stress-strain curve. When the spring breakage increases to a certain number of forms, the steady variation of crack appearance in small cylinders gradually increases randomly with the occurrence of instability. At this point, the bearing capacity of the small cylinders increases, while the overall compressive stress decreases, with the stress-strain curve reaching the ultimate bearing stress. Therefore, a mesoscopic approach was adopted to describe the macroscopic failure mechanism of ancient pagodas under pressure.
Based on the theoretical analysis above, ancient pagodas under pressure are damaged owing to the failure of small prisms as a result of the gradually broken pagoda structure. From the model diagram of the pagoda structure under pressure with the mesoscopic conditions illustrated in Fig.4, the damage variation D can be described by the classical damage mechanics theory proposed by Rabotnov et al.[23].
where AD is the area without bearing capacity owing to failure, and A is the undamaged block area. From Eq.(1), AD=0 and D=0 means that no damage occurs in the pagoda; AD=A and D=1 indicates the damage to the ancient pagoda under pressure. Therefore, the damage to the ancient pagodas varies from 0 to 1.
The damage evolution equation of masonry represented by a Weibull distribution function is used to calculate the damage variation of pagodas under pressure. The equation, with the convenient reference to physical quantity and simple formula form, is expressed as follows[21-22].
Where a, b, and η are coefficients, ε is the strain, fm and εm are the limiting stress and corresponding strain, respectively, and E is the modulus of elasticity of the masonry.
2.3 Numerical simulation
2.3.1 Numerical model
Based on the size of the structure model, a finite element method (FEM) model was established with 10-node hexahedron elements.The blocks and mortar are equivalent to a continuum material the calculation parameters of which can be defined based on the test results. The density of the structure was selected as 2 100 kg/m3, and the Poisson's ratio was 0.15[24]. The damage constitution law was adopted for the calculation using Eq.(5).
where σ is the compressive stress of the masonry, ε is the compressive strain,η has a numerical value of 1.633. The fm and εm are decided based on the test results of masonry blocks as Fig.5 shows. And the fm can be defined as 5.6 MPa, εm can be defined as 0.04.
Based on the value of the parameters, Eq.(5) can be expressed as
2.3.2 Numerical results
The calculation results of the equivalent plastic strain are presented in Fig.6. From Fig.6, the maximum strains match the experimental results of the cracks in the models, which can be seen in Fig.7. The numerical model captures the overall deformation of the structure with reasonable accuracy. The values around the hole and the intersection of the tower and eaves are larger than those of the other parts, indicating that the sections crack easily.
3 Results and discussion
3.1 Failure phenomenon
The failure phenomenon of the ancient brick pagoda under pressure was characterized by brittleness. Based on the failure phenomenon, the cracking mode of the model is similar to the failure characteristics. Three stages were identified for the deformation characteristics of Model 3.
During the first stage,at 40%~60% of the ultimate load, cracks were generated at the initially applied pressure, and the vertical cracks occurred at the edge of the mortar. As the load approached approximately 40% of the ultimate value, cracks first appeared on the vertical mortar joints at the corner of the pagoda top with small cracks in the adjacent bricks, as shown in Fig.7 (a). During this period, cracking occurred in the brick interior on the vertical mortar joints, and only the single blocks were crushed under pressure. Under the same load, the cracks extended spontaneously.
At 60%~80% of the ultimate loading, at the crack expansion and extension stage, with the increase in loading, the cracks were stretched further with cracking sounds in the inner bricks. At the same time, new cracks occurred randomly at different positions in the bricks, with cracks extending along the mortar joints. The expansion and extension of the cracks increased in width and length and led to the formation of significant cracks in the later stage. With the continuous increase in loading, the main cracks eventually contributed to the
formation of penetrating cracks. Some bricks disintegrated, and staggered joints occurred at the cracks of the structure, as shown in Fig.7 (b). During this period, new cracks randomly occurred in the bricks, which presented upward and downward expansion trends. The main cracks penetrated with increasing crack width.
At 80%~100% of the ultimate load, during the failure stage of the penetrating cracks, the main cracks penetrated all through, and the pagoda structure was divided into several small brick prisms. With the increase in loading, the width of the main cracks expanded further, and staggered layers appeared at the cracks on the bricks. Moreover, due to the swelling deformation of the pagoda, the test was completed with the failure of the model caused by instability and decreased bearing capacity. Fig.7 (c) presents the final failure diagrams of the three models under loading. During this period, no new cracks appeared, which indicated the expansion and extension of the initial and penetrating cracks as well as the increase in the main crack widths. Consequently, instability occurred as the model was divided into numerous small prisms.
Regarding the three models, the failure mode of the ancient brick pagodas is described as follows. The cracks at the top edge and corner of the pagoda expanded downwards to form a penetrating crack with the increase in loading. In addition, staggered layers occurred at the cracks with a division into many small prisms, which further led to the instability of the pagoda.
3.2 Structure deformation under load
The equivalent axial stress and strain of the whole structure at different positions were calculated by Eqs.(7) and (8).
where σce,εce is the equivalent axial stress and strain, FN is the value of the pressure force, AE is the section area of the first floor of the model; Δ is the total axial deformation of the first floor, H is the total height of the first floor.
Then the stress-strain curve was determined, as presented in Fig.8. It can be seen from Fig.8 that the slope of the curve shows an increasing trend except for some short stages. The initial stage of the model compression shows the compression and extrusion of internal gray joints. When the strain increases rapidly, the deformations under stress are small, and the slope of the curve is equally small. When the gray joint is squeezed and compacted, the structure enters the stage of joint force between the block and gray joint. During this period, the slope of the curve increases, and the stress-strain curve has a linear growth trend. When the stress reaches the peak value, the curve exhibits an upward convex form until the model is damaged when the stress reaches the maximum value. Afterward, the stress-strain curve displays a downward trend.
With the decrease in the block size, the peak stress value of the stress-strain curve decreases, and the ultimate strain value increases. These trends indicate that the initial damage to the structure affects the decrease in the peak stress and the increase in the corresponding peak strain of the pagoda under compression. The slope of the curve decreases with the increase in the initial damage, suggesting that both the elastic modulus and the structural stiffness of the tower decreases with the increase in the initial damage to the ancient pagoda.
The results of the compressive strength of the model under compression are presented in Table 1. From Table 1, the ratio of the cracking load to the ultimate load of the model ranges between 0.4 and 0.6. The cracking load and ultimate load are positively correlated with the block size, which demonstrates that the ultimate bearing capacity of the ancient masonry under compression is closely related to the initial damage state of the structure.
Load-displacement curves were determined for the three models under different loads, as displayed in Fig.9. It can be observed from Fig.9 that at the initial stage of the model compression, the main deformation of the tower body is vertical. When the load enters the initial crack generation stage, the horizontal and transverse deformation of the tower begins to increase. The model changes from compression deformation to horizontal tension and outward bulging deformation. When the model finally fails, the horizontal deformation of the model becomes the largest, followed by the transverse and vertical deformation.
Due to the low strength of the glutinous rice mortar used in the model, the compressive bearing capacity of the mortar at the mortar joints was low during the initial compression stage, which demonstrated compression and extrusion phenomena. When cracks were formed, micro cracks appeared on the block leading to the complex stress state; the tensile stress continued to increase with the load.
The horizontal deformation of the tower also increases with crack width and depth. It is clear from Fig.9 that the deformations in different directions of the pagoda vary with block size. The vertical and horizontal deformations of the tower increase with the decrease in the block size, which indicates that the changes in the compressive failure of the ancient brick pagoda are related to the initial damage forms of the tower.
The displacement variations of the three test models in three directions were analyzed. With the increasing load, the transverse displacement of the pagoda increased gradually, showing the outward expansion phenomenon. The horizontal displacement of the pagoda was higher than its vertical displacement, indicating that the transverse deformation of the pagoda was larger than its vertical deformation, and the bulging phenomenon of the tower was apparent.
3.4 Damage analysis
From the compression experiment, the equivalent stress and strain of the structure and some blocks were calculated, and the compression failure mechanism of the pagoda masonry was analyzed.The ancient pagoda is composed of two different materials: low-strength mortar and block. The structure had low tensile strength. Because insufficient ash joints were used in building the structure, there were several stress states at the ash joints under compression, which resulted in the vertical compressive and transverse tensile stresses of the bricks. When the tensile strain induced by the vertical compression exceeded its ultimate value, parallel loading cracks occurred in the inner part of the block. The transverse tensile stress of the mortar increases with the increase in load. Then, the cracks in the inner part of the block extend faster.
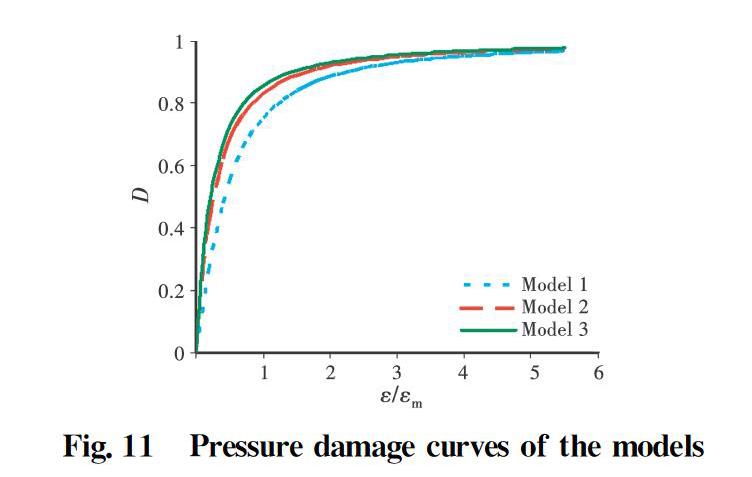
The damage curves of the three models
presented in Fig.11 are calculated using Eq.(2) based on the pressure test results of blocks. As shown in Fig.11, three damage curves vary rapidly with the increase of strain, and the structure is severely damaged when ε=(0.1∶1.5)εm; however, the damage curves change slowly afterward. In addition, under the influence of the initial damage, the damaged slope of Model 3 under compression is higher, the damage speed is high, the crack penetration speed under compression is faster, and the model is more easily damaged under compression. These observations signify that the damage speed of the brick pagoda is positively correlated with the initial damage state of the structure.
4 Conclusions
Three 1/8 scaled models of the first story of Xuanzang pagoda were built using 1, 1/4, and 1/8 scaled original black, and compression tests were performed. The conclusions are presented in the following paragraphs.
Ancient masonry pagodas are brittle under compression. The failure process can be classified into three stages: crack of gray joints, crack propagation and elongation and crack transfixion. The compressive failure mode of the ancient masonry pagoda is influenced by the cross-sectional areas of the eaves and the tower structure. During the compressive failure of the ancient masonry pagoda, cracks appear in the block at the top corner of the tower body and extend downwards along the vertical gray cracks, forming penetrating cracks. The tower body is divided into several small prisms, resulting in the instability and failure of the tower structure.
The ratio of the cracking load to the ultimate load of the ancient masonry pagoda ranges between 0.4 and 0.6 from the axial equivalent stress and strain of the entire structure. The ultimate bearing capacity of the ancient masonry pagoda is positively correlated with the initial damage to the model. Before the load generates crack propagation and elongation, the model is dominated by vertical compression deformation, followed by the appearance of outward tension and bulging deformation of the tower structure.
From the load-strain relationship of the internal blocks of the structure, the initial stage of compression of the ancient masonry pagoda is characterized by the compression deformation of the blocks. When the load enters the crack propagation and elongation stage, the tensile strain on the blocks increases. With the increase in load, the tensile strain on the blocks increases from top to bottom. The damage change to the ancient masonry pagoda under compression is most significant when the equivalent strain reaches a particular value. Cracks in the tower body develop rapidly and the tower structure is severely damaged. The damage speed of the ancient masonry pagoda is positively correlated with the initial damage state of the pagoda tower.
Acknowledgements
We would like to acknowledge the help extended by the staff at the Structural Engineering Laboratory of Xi'an University of Technology in conducting the experiments. We are grateful to the anonymous reviewers for their comments. The financial support received from the National Natural Science Foundation of China (Grant No. 51778527) are gratefully acknowledged.References:
[1] SHI C X. The theory and design of masonry strcture [M]. 3rd ed. Beijing: China Architecture and Building Press, 2014.
[2] MCNARY W S, ABRAMS D P. Mechanics of masonry in compression [J]. Journal of Structural Engineering, 1985, 111(4): 857-870.
[3] LOURENCOP B, BARROS J O, ALMEIDA J C. Characterization of masonry under uniaxial tension [R]. Universidad do Minho, Braga, 2002.
[4] EWING B D, KOWALSKY M J. Compressive behavior of unconfined and confined clay brick masonry [J]. Journal of Structural Engineering, 2004, 130(4): 650-661.
[5] SARANGAPANI G, VENKATARAMA REDDY B V, JAGADISH K S. Brick-mortar bond and masonry compressive strength [J]. Journal of Materials in Civil Engineering, 2005, 17(2): 229-237.
[6] VENKATARAMA REDDY B V, LAL R, NANJUNDA RAO K S. Enhancing bond strength and characteristics of soil-cement block masonry [J]. Journal of Materials in Civil Engineering, 2007, 19(2): 164-172.
[7] VENKATARAMA REDDY B V, UDAY VYAS C V. Influence of shear bond strength on compressive strength and stress-strain characteristics of masonry [J]. Materials and Structures, 2008, 41(10): 1697-1712.
[8] PAN Y, WANG X Y, GUO R, et al. Seismic damage assessment of Nepalese cultural heritage building and seismic retrofit strategies: 25 April 2015 Gorkha (Nepal) earthquake [J]. Engineering Failure Analysis, 2018, 87: 80-95.
[9] HUANG L, WANG H, CHEN S Y. Experimental research on compressive behavior of grouted block masonry with low-strength mortar [J]. Engineering Mechanics, 2012, 29(10): 157-161.
[10] TAO Q W, SHI C X. Influence of hole shape on compression strength of perforated brick masonry and value of compression strength [J]. Building Structure, 2005, 35(9): 20-23.
[11] WANG Q W, SHI Q X, HEI W W. Experimental study on basic mechanical properties of DP-type fired perforated clay brick masonry [J]. Journal of Building Structure, 2017, 38(12): 122-130.
[12] KAUSHIK H B, RAI D C, JAIN S K. Stress-strain characteristics of clay brick masonry under uniaxial compression [J]. Journal of Materials in Civil Engineering, 2007, 19(9): 728-739.
[13] GUMASTE K S, NANJUNDA RAO K S, VENKATARAMA REDDY B V, et al. Strength and elasticity of brick masonry prisms and wallettes under compression [J]. Materials and Structures, 2007, 40(2): 241-253.
[14] LUMANTARNA R, BIGGS D T, INGHAM J. Uniaxial compressive strength and stiffness of field-extracted and laboratory-constructed masonry prisms [J]. Journal of Materials in Civil Engineering, 2014, 26(4): 567-575.
[15] WU F, LI G, LI H N, et al. Strength and stress-strain characteristics of traditional adobe block and masonry [J]. Materials and Structures, 2013, 46(9): 1449-1457.
[16] LIU G Q, YAN Y Q, SHI C X. Research on the unified model of the compressive constitutive relations of masonry [J]. Journal of Hunan University (Natural Sciences), 2009, 36(11): 6-9.(in Chinese)
[17] DANG C N, MURRAY C D, FLOYD R W, et al. Analysis of bond stress distribution for prestressing strand bystandard test for strand bond [J]. Engineering Structures, 2014, 72: 152-159.
[18] ZENG X M, YANG W J, SHI C X. Study of constitution relationship model for compressive masonry[J]. Sichuan Building Science, 2001, 26(3): 8-10.(in Chinese)
[19] WANG S H, TANG C A, WU X. Constitutive damage model and numerical methods for cracking process of masonry structures [J]. Journal of Building Structure, 2003, 24(2): 64-69.
[20] YANG W Z, FAN R. A generic stress-strain equation for masonry materials in compression [J]. Journal of Zhengzhou University (Engineering Science), 2007, 28(1): 47-50.
[21] YANG W Z, CAO W W, WANG Q. Research on stochastic damage constitutive relation of masonry subjected to axial loading [J]. Zhengzhou University (Natural Science Edition.), 2013, 45(2): 104-109.
[22] YANG W Z. Constitutive relationship model for masonry materials in compression [J]. Building Structures, 2008, 38(10): 80-82.
[23] RABOTNOV Y N, LECKIE F A, PRAGER W. Creep problems in structural members [J]. Journal of Applied Mechanics, 1970, 37(1): 249.
[24] LU J L, LI C L, HAN X, et al. Numerical simulation and test verification of seismic damage for a brick masonry pagoda [J]. Journal of Vibration Engineering, 2020, 33(2): 364-371.
(編辑 章润红)
