火灾后SRC柱-RC梁框架结构性能反复加载试验研究

李俊华 李权平 张磊 黄梦迪

摘 要：對一个SRC柱RC梁框架在火灾后与另一个对照框架在常温下进行了低周反复加载试验，研究了该框架的火灾后性能，评价了框架的承载力、刚度退化、延性、耗能能力、累积损伤，同时对PΔ效应进行了分析。试验结果表明，与未暴露在火灾的SRC柱RC梁框架相比，火灾后SRC柱RC梁框架的承载力降低、刚度减小、延性系数下降、累积损伤增大，且PΔ效应更为明显。由于框架柱截面中有核心钢的存在，SRC柱RC梁框架在火灾后的滞回曲线仍保持饱满，破坏前的承载力可以保持在较高的水平，依然表现出良好的耗能能力。其塑性极限转动超过0.04 rad，可以满足中国抗震设计规范的要求。

关键词：型钢混凝土;框架;火灾;反复荷载;抗震性能

1 Introduction

Steel reinforced concrete （SRC） structures that combine the advantages of reinforced concrete （RC） and steel， are applied increasingly in modern architecture， especially in high-rise and super-tall buildings. High-rise and super-tall buildings are more likely to have accidental fires than ordinary buildings due to their large area and complex use. As SRC structures are common structural elements in high-rise and super-tall buildings， their fire behavior has attracted much attention.

Studies have investigated the fire performance of SRC structures. Malhotra and Stevens[1] found that the fire resistance of SRC columns increased with the increasing thickness of the concrete cover. Huang et al.'s test results and numerical analyses[2-3] indicated that the cross-sectional size， boundary conditions， and load ratio affected the fire resistance of the SRC column. Young and Ellobody's numerical analysis[4] showed that axially restrained composite columns behave differently in fire compared to unrestrained columns. Based on test results， Correia and Rodrigues[5] pointed out that the surrounding structures had a significant influence on the fire performance of the column when the load level was low. Han et al.[6]， based on the results of finite-element analysis， proposed a simplified calculation method for the fire resistance of the SRC column. Wang et al.[7] used numerical analysis to investigate the fire performance of circular tubed SRC columns and found that the fire resistance decreased with the increase of the load ratio and the wall thickness of the steel tube.

Generally speaking， SRC structures show better fire performance compared with pure steel structures. Because of the protection provided by the concrete to the inner shaped steel [8]， it is very likely that the SRC structure survives a fire. However， the mechanical properties of the concrete would be greatly degraded after the fire， and the reliability of the structure would be reduced， resulting in potential safety hazards. Therefore， evaluating the performance of fire-damaged SRC structures is critical. Tao et al.[9] tested the bond strength of SRC columns after fire， and found that there was significant degredation of the bond after fire exposure. Li et al.[10]， based on test results， put forward a method of calculating the strength of the bond of SRC structures after exposure to fire. Du et al.[11] and Wang et al.[12] used finite element analysis to study the mechanical properties of the SRC column in the whole process of rise and fall of the temperature of the fire and found that the structures surviving the rising fire temperature may fail in the cooling stage due to the hysteresis of section temperature. Han et al.[13] found that after the SRC column fully cooled down to the ambient temperature， the proportion of the load carried by the steel section increased a lot. Wang et al.[14] and Shi et al.[15] carried out experimental research and numerical simulation analysis on the seismic performance of SRC columns after fire. Li et al.[16] put forward the calculation method for the shear capacity of SRC columns after fire exposure. Song et al.[17] established a finite element analysis model to simulate the response of the SRC column to SRC beam joints during the heating and cooling phases. Using the proposed model， the joint rotational deformation， which could not be measured during the test， was investigated.

The aforementioned research mainly studied the performance of SRC construction members after fire. These studies have provided valuable knowledge to understand the post-fire performance of SRC structures. Studies on SRC frames are very important to further understand the performance of SRC structures. Zhang et al.[18] tested the fire-exposed SRC column-SRC beam frame considering the influence of fire duration and load ratio on the failure mode， deformation performance and residual bearing capacity. Li et al.[19] found that due to the existence of core steel in the section of column and beam， the hysteresis loops of the SRC frame after exposure to fire remained plump， and the load bearing capacity remained at a relatively high level before destruction. Wang et al.[20-22]， based on test results and finite element analysis， analyzed the deformation and internal force of the SRC column-SRC beam frame under the whole process of fire heating and cooling. Li et al.[23] found from test results that exposure to fire changed the failure mode of RC frames. The frame under room temperature failed in the form of beam-end plastic hinging， but after being exposed to fire， the failure mode changed to shear-bond failure in the column. However， there has been no research on the mechanical behavior of the SRC column-RC beam frame structures after exposure to fire.

When the span of the beam is not too large， the SRC column-RC beam composite frame can reduce the cost of a project and simplify the construction. Therefore， this kind of structure has a good application in engineering. In light of this， this paper presents a low-cycle repeated loading test to investigate the seismic behavior of the SRC column-RC beam frame after fire to provide a basis for the performance evaluation and repair of such frames after being fire-damaged.

2 Experimental program

2.1 Test specimens

Two frames pecimens， one single-story and one single-bay， were prepared. One， referred to as RCF， was used to conduct a post-fire test， the other， referred to as RC， was used to do a comparative experiment under ambient temperature. Both frames consisted of two SRC columns， one RC beam， and one foundation beam， in which the columns were anchored. Fig.1 shows the two frames.

As shown in Fig.1， a hotrolled H-shaped steel HM150×100×6×9 （i.e.， height=150 mm， width=100 mm， web thickness=6 mm， and flange thickness=9 mm） was embedded in an SRC column and a short steel bracket with a length of 70 mm was welded to the flange of the shaped steel to connect the beam steel bars. The profile size of the bracket was 116×80×10×10 （i.e.， height=116 mm， width=80 mm， web thickness=10 mm， and flange thickness=10 mm） and a fillet weld 10 mm thick was used in the connection between the bracket and the steel column. To transfer the internal forces of the top and bottom steel bars of the RC beam， 10 mm thick horizontal stiffeners welded to the column steel parallel to the upper and lower flanges of the brackets were used in the frame joints. Fillet weld 10 mm thick was also used in the connection between the stiffeners and the steel column.

The sectional area of the frame column was 250 mm×250 mm， and four deformed bars with a diameter of 18 mm were used as the longitudinal bars of the column. The sectional area of the frame beam was 200 mm×180 mm （i.e.， height=200 mm and width=180 mm）， and four deformed bars with a diameter of 12 mm were used as the top and bottom longitudinal bars， respectively， in the beam. The sectional area of the foundation beam was 400 mm×400 mm， and four deformed bars with a diameter of 20 mm were used as the top and bottom longitudinal bars in the beam. For the beams and columns， transverse bars were placed at a spacing of 50 mm and 100 mm in the critical region of 500 mm and the remaining part， respectively. For the core area of the joint， U-hoop was installed at a spacing of 50 mm to strengthen the restraint on the concrete， and the hoop was welded on the web of the steel bracket.

In order to measure the temperature at different positions of the frame while the fire was heating up and cooling down， thermocouples were arranged in the sections of the specimen RCF at the mid-height of the left column， at the mid-span of the beam and at the core area of the left beam-column joint. Layouts of the thermo-couples are shown in Fig.2.

2.2 Material properties

Table 1 shows the yield strength， tensile strength， and elastic modulus of the steel section and reinforcing bars measured at room temperature. Grade 40 concrete was used for the test specimens. Average cubic strength of the concrete measured at room temperature was fcu，k=57.6 MPa （150 mm ×150 mm × 150 mm）， and the compressive strength was f′c=0.67×57.6=38.6 MPa according to GB 50010-2010.

2.3 Heat treatment

After curing for 28 days， the RCF specimen was heated by exposing it to fire in a furnace. The length， width and height of the furnace were 4 000 mm， 1 500 mm and 3 000 mm， respectively. There were eight diesel nozzles in the furnace and the temperature was adjusted by controlling the delivery and atomization of diesel oil in the nozzles. In the test， the specimen was subjected to fire on four sides for 75 minutes. Before the fire test， fire-proof cotton was wrapped around the foundation beam at the bottom of the frame to reduce high-temperature damage. When the fire duration reached the end of the scheduled time， the flame was extinguished and the furnace door was opened so that the specimen could be cooled naturally. The heating and cooling curve recorded by the thermocouple in the furnace is shown in Fig.3.

It should be noted that in a real fire situation， thermal creep deformation will occur in the steel and concrete materials in a loaded frame. However， owing to the limitation of the furnace facility， the specimen was not loaded during the exposure to fire in the current test. Further research is required in the future to address this issue.

2.4 Loading Scheme

Loading was carried out on the loading device shown in Fig.4. The specimen was fixed on the pedestal beam at the bottom of the device. Lateral load was exerted by an MTS hydraulic actuator and transmitted to the frame through the limit baffle at the top of the specimen. Vertical load was exerted on the L-shaped beam by a hydraulic jack， with a slide trolley on the top of the jack， which can slide freely when loading. The four-bar linkage mechanism in the device ensured that the upper and lower planes of the specimens remained level throughout the test.

The load was applied in two stages. First， 1 276 kN vertical load calculated according to the axial compression ratio of the frame column of 0.2 was applied on the top of the column and kept constant， and then horizontal force was applied at the beam column junction center through the MTS actuator. Displacement controlled cyclic load was applied for lateral loading. One load cycle was applied at every 2 mm increase up to 10 mm， and then three load cycles were applied at every 10 mm increase until the specimen failed， as shown in Fig.5. Specimen failure was defined as：1） drift corresponding to 85% of the peak load （i.e.， 15% strength degradation after the peak strength） or 2） significant strength degradation and obvious larger plastic deformation. The lateral load and displacement of the specimen was measured by transducers inside the hydraulic actuator.

3 Experimental results

3.1 Test results of fire heating

As shown in Fig.6， after fire heating treatment， the surface of the specimen was light yellow and obvious damage traces were left. First of all， due to the increase of internal water pressure at high temperature， the concrete of the specimen was found to burst locally. At the same time， for the evaporation of water， many microcracks appeared on the surface of the specimen. On the other hand， the strength of concrete was greatly reduced. The compressive strength of concrete cubes treated with the same heating treatment as the frame was tested， and the residual compressive strength of the cube was 33.5 MPa，which was just about 57.2% before fire.

Fig.7 shows the temperature-time curves of each measuring point in the section of the beam， column and joint of the RCF specimen. Table 2 gives the highest temperature of each measuring point in the whole heating and cooling process. It can be seen from Fig.7 and Table 2 that： 1） in the section of beams， columns and joints， the closer to the surface of components， the faster is the temperature rise and fall. 2） The temperature of the column section was higher than the temperature of the joint section when the distance from the measuring point to the surface of the component was the same. This was because the reinforced concrete beam connected with the joint causes the three-sided fire state of the joint， which makes the rate of heating and the maximum temperature lower than at the end of the column.

3.2 Load-displacement relationship

Fig.8 shows the lateral load-displacement relationship of the specimens at the top of the frame. Fig.9 shows the failure mode of the specimens at the end of the test.

In the RC specimen without exposure to fire， a slight crack began in the beam close to the joint at P=147 kN corresponding to Δ=20 mm. Then cracks appeared in the bottom of the column at P=205 kN， corresponding to Δ=30 mm， and in the beam-column joint area at P=265 kN， corresponding to Δ=50 mm. The peak strength Pu reached 274 kN at Δ=70 mm. Meanwhile， the concrete of the beam near the joint spalled to form plastic hinges. The end of the beam was seriously damaged， and the concrete at the end of the column also spalled to form plastic hinges at P=270 kN after peak-strength， corresponding to Δ=80 mm. Ultimately， RC failed at Δ=120 mm because of serious destruction of column foot concrete， and the load dropped to 232 kN， which was less than 85% of the peak load. But at this time， the joint still maintained a good state， showing the characteristics of strong column， weak beam， and stronger joint.

In the RCF specimen after exposure to fire， the crack began in the beam at P=56 kN， corresponding to Δ=10 mm. Then cracks appeared in the bottom of the column at P=103 kN， corresponding to Δ=20 mm， and in the beam-column joint area at P=223 kN， corresponding to Δ=60 mm. The peak strength Pu reached 248 kN at Δ=80 mm， and the concrete of the beam near the joint spalled to form plastic hinges simultaneously. The end of the beam was seriously damaged， and the concrete at the end of the column also spalled， forming obvious plastic hinges at P=246 kN after peak-strength， corresponding to Δ=90 mm. Ultimately， RCF also failed at Δ=120 mm because of serious destruction of column foot concrete， and the load dropped to 210 kN with one diagonal crack running through the joint.

In a word， the failure process of the non-fire RC specimen and the fire-damaged RCF specimen was basically the same. However， due to the deterioration of concrete strength after fire， the cracks appeared earlier and developed faster in the RCF specimen compared with the RC specimen. Despite the fire， the RCF joints had only one obvious inclined crack， and there was almost no damage inside the joints. This was because the section steel and its horizontal stiffeners in the column improved the shear capacity of the joint， so the joint could maintain a high bearing capacity level and meet the strong-joint weak-member andstrong-column weak-beam requirements of seismic design even after exposure to fire.

3.3 Envelope curve

Fig.10 shows the envelope curve of the specimens. Table 3 lists the yield strength Py， peak strength Pu， yield displacement Δy， ultimate displacement Δu， and ductility ratio μ of the specimens. Fig.11 shows the definition of the yield and ultimate displacements in the load-displacement relationship. The yield displacement Δy was defined as the displacement of the equivalent elastic-plastic envelope curve defined by the secant stiffness at 60% of the peak strength. The ultimate displacement Δu was defined as the post-peak displacement corresponding to 0.85Pu. The yield strength Py was defined as the strength corresponding to the yield displacement Δy. The ductility ratio μ was defined as the ratio of yield displacement Δy and ultimate displacement Δu.

It can be seen from Fig.10 and Table 3 that after exposure to fire，the maximum load of the specimen decreased， but the displacement corresponding to the maximum load increased. The yield and peak strength of the RCF specimen were 219.6 kN and 248.2 kN， respectively， which were 9.1% and 9.5% less than that of the RC specimen. The yield displacement and ultimate displacement of the RCF specimen were 47.4 mm and 119.8 mm， respectively， which increased by 33.5% and 1.4% compared with the RC specimen. The yield displacement increased more， but the ultimate displacement did not differ much， indicating that the fire reduced the capacity of the steel reinforced concrete frame to resist the load and weakened the deformation capacity. The change in the displacement ductility after the fire also reflected this. The RCF and RC specimens exhibited the ductility of μ=2.52 and 3.33， respectively. The displacement ductility coefficient of the RCF specimen post-fire decreases by 24.3% compared with that of the RC specimen without exposure to fire at room temperature.

3.4 Secant stiffness

When the stiffness of the frames is significantly decreased， large displacement of a structure occurs even at a low earthquake load level， which induces the instability of the structure. Fig.12 shows the variation in secant stiffness at each load cycle to investigate the degradation in stiffness. Secant stiffness Kj was defined as the cumulated strength divided into the cumulated displacement at each load cycle.

where Pij and Δij are the peak load and corresponding displacement， respectively， at the ith cycle of displacement j; and n is the load cycle at each displacement level.

It can be seen from Fig.12 that as the displacement increases， the secant stiffness of both specimens decreases significantly due to the deterioration of the structural integrity. Table 4 gives the comparison of the secant stiffness of the two specimens under initial displacement （loading displacement is 10 mm）， yield displacement and ultimate displacement. From the data in Table 4， it can be seen that the stiffness of the frame decreases significantly after the fire. The initial stiffness K0， yield stiffness Ky and ultimate stiffness Ku of RCF decreased by 34.4%， 37.1% and 6.2%， respectively， compared with the RC specimen. This was because the fire reduces not only the strength， but also the elastic modulus of the concrete， which leads to the decrease of stiffness of components. From Fig.12， it can also be seen that after the peak load， the stiffness curves of the two specimens gradually converge. The main reason is that the concrete at the end of the beam and the foot of the column gradually withdrew from work when the frame was near failure. The stiffness of the specimens was mainly provided by the steel in the column and the core concrete wrapped in it， so the stiffness was decreasing.

3.5 Energy dissipation capacity

Energy dissipation capacity refers to the ability of a structure to absorb and dissipate seismic energy， which can be expressed by equivalent viscous damping ratio he. As shown in Fig.13， equivalent viscous damping ratio he  is defined as

where SABCD is the energy dissipation per load cycle defined as the area enclosed by a complete load cycle （i.e.， area enclosed by curve ABCDA）; SBOE is the triangular area enclosed by points B， O， and E; and SDOF is the triangular area enclosed by points D， O， and F.

Fig.14 shows the variation of he of the two specimens according to the displacement based on the hysteresis loops formed by the first load cycle under different displacements. For both RC and RCF， the equivalent damping ratio first decreased due to concrete cracking and continuous withdrawal from work and then increased with the increase of displacement as the section steel in the frame column gradually played an increasingly important part in load bearing. Before the displacement reached 40 mm， the equivalent damping ratio of the RCF specimen was larger than that of the RC specimen. When the displacement was greater than 40 mm but less than 100 mm， the equivalent damping ratio of the RCF specimen was smaller than that of the RC specimen. After the displacement of 100 mm， the equivalent damping ratio of RC and RCF tended to be the same，reaching 0.202 and 0.205， respectively， showing good energy consumption. The reason for this phenomenon is related to the hysteresis characteristics， as shown in Fig.8， and the deformation performance， as shown in Fig.10. For the RC specimen，when the displacement was less than 40 mm， the load changed rapidly during loading and unloading， and its hysteresis loop was not as full as that of the RCF specimen， which led to a smaller equivalent viscous damping ratio. As mentioned above， the fire caused the strength of the concrete of the RCF specimen to decrease. With the further increase of displacement， the load corresponding to the RCF specimen was less than that of the RC specimen under the same displacement， and the plumpness of its hysteresis loop decreased， resulting in the equivalent viscous damping ratio gradually becoming smaller than that of the RC specimen. When the displacement was greater than 100 mm， the hysteretic behavior and deformation performance of the specimens were mainly executed by the core steel in the frame column， so the equivalent viscous damping ratio was approximately the same.

3.6 Plastic rotation capability

The plastic rotation capacity of the frame can be expressed by plastic rotation angle θp， which is defined as the difference between the total rotation angle and the elastic rotation angle

The data in Table 5 shows that the yield plastic rotation angle and the peak plastic rotation angle of the RCF specimen after exposure to fire increase and the ultimate plastic rotation angle decreases compared to that of the RC specimen at room temperature without exposure to fire. The ultimate plastic rotation angles of the RC specimen without exposure to fire and the RCF specimen after exposure to fire are 0.046 6 and 0.042 0 rad， respectively， both of which meet the 0.02 rad limit stipulated in the current Chinese Code for Seismic Design of Buildings （GB 50011-2010）[24].

3.7 Cumulative damage

Cumulative damage refers to the damage accumulated with the increase of the number of load cycles when a structure is subjected to seismic loads. The cumulative degree of damage directly determines whether the structure can continue to bear the load. Generally， it can be expressed by damage index D. Diao et al.[25] developed a simple cumulative damage model of the frame based on the following mechanical state， as shown in Fig.15.

When the structure is subjected to external forces in an ideal state， the load-displacement curve moves along the elastic routes OA and OB （as shown in Fig.15）， so the work W done by the external forces can be expressed as

However，there must be damage in the actual loading process of the structure， and so the curve moves along the route OCDEFO. In this case， the work W done by the external force is transformed into three parts， namely， elastic deformation energy， plastic deformation energy， and damage dissipation energy， which are expressed by We， Wp and WD， respectively.

Then， the cumulative damage index D is determined as follows.

The relationship between damage index D and load cycle n is shown in Fig.16. It can be seen clearly from Fig.16 that the cumulative damage index increases with the increase of the number of load cycles and fire action has a significant effect on the cumulative damage of the specimens. For the RC specimen without exposure to fire， the cumulative damage index D increases linearly with the increase of the number of load cycles， while for the RCF specimen after exposure to fire， the cumulative damage index D increases nonlinearly. When the number of load cycles was less than 10， the cumulative damage index D of the RCF specimen increased rapidly with the increase of the load cycles， and then the growth rate slowed down with the increase of the load cycles. This was because the concrete in the frame beams and the columns bore a large part of the load on the cross-section at the initial stage of loading， but the fire reduced the strength of the concrete and accelerated the strength attenuation， which， after the fire， led to faster growth of the cumulative damage of the specimen under repeated loading. With the increase of the number of load cycles， the concrete continued to withdraw from the work， and the load in the frame beam and column was mainly borne by the steel and reinforcement， so the growth trend of the cumulative damage of the specimen under repeated load was slowed down. In general， thedamage index D of the RCF specimen RCF post-fire was significantly higher than that of the RC specimen without exposure to fire under the same cycle times， indicating that the cumulative damage of the frame under repeated load was more serious due to fire action.

3.8 P-Δ effect

P-Δ effect refers to the bending moment effect of the axial force in the vertical direction due to the lateral horizontal displacement in the process of structural loading. It is an important factor affecting the bearing capacity of structures under horizontal loads， resulting in the reduction of the bearing capacity of the structure.

Fig.17 shows the deformation diagram of the frame under load. P is the horizontal force acting on the top of the frame column， and N1 and N2 are the axial forces acting on the frame column. NA and NB are the axial resistance and MA and MB are the resistance moment at the bottom of the frame column.

As shown in Fig.17， for point A at the bottom of the frame column， without considering the P-Δ effect， the following results can be obtained according to the equilibrium conditions of internal and external forces and bending moments.

Considering the P-Δ effect， the result becomes

where P0 is the horizontal force on the top of the frame column when the same axial resistance and bending moment occur at the bottom of the frame column.

The following conclusions can be drawn.

The horizontal force reduction factor η is introduced to indicate the P-Δ， as follows.

When the axial forces N1 and N2 applied to the frame columns are equal to N， the calculation formula becomes

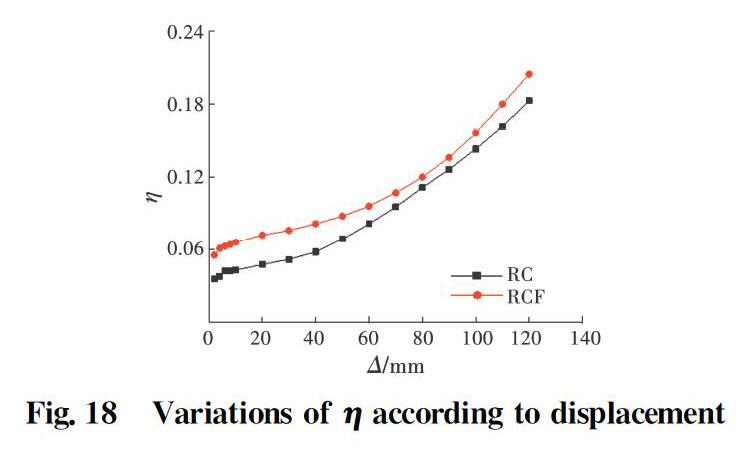
Fig.18 shows the variations of η according to the displacement of the specimens. When the loading displacement is small， horizontal force reduction factor η is relatively small， hence， the P-Δ effect is not obvious whether the specimen has been exposed to fire or not. With the increase of the displacement， horizontal force reduction factor η， as well as the influence of the P-Δ effect， increases rapidly， resulting in the decrease of the bearing capacity of the frame. On the other hand， the η value of the RCF specimen post-fire increases significantly compared with that of the RC specimen without exposure to fire at the same horizontal displacement， which indicates that the P-Δ effect of the frame is more obvious due to fire damage.

4 Conclusion

In the present study，fire test was first performed on one SRC column-RC beam frame， then quasi-static tests were conducted on this frame and on a comparative frame at room temperature without exposure to fire. The seismic performance of the SRC column-RC beam frame after exposure to fire was evaluated based on the test results. The primary test results are summarized as follows：

1） The high fire temperature reduced the strength of the concrete. In this experiment， the compressive strength of the concrete cube post-fire was only about 57.2% of that under normal temperature without fire. Due to the degradation of the strength of the concrete， the concrete cracking and crack development in the SRC column-RC beam composite frame under fire were faster than those under normal temperature without fire.

2） The degradation of the concrete material properties caused by fire affected the seismic performance of the frame. Compared with the frame without fire， the bearing capacity， stiffness and ductility of the frame post-fire were reduced by 9.5%， 34.4% and 24.3%， respectively. In addition， the cumulative damage to the frame under repeated loading increased， and the P-Δ effect was more obvious post-fire.

3） Due to the existence of the core steel in the frame column， the hysteretic curve of the SRC column-RC beam composite frame post-fire was still full. Post-fire， the frame could still maintain a high load carrying level， had good energy dissipation performance and load cycle resistance ability， and its plastic limit angle was more than 0.04 rad， which fully meets the requirements of the limit value of plastic rotation specified in the seismic code of China.

Acknowledgements

The authors would like to acknowledge the financial support from the National Natural Science Foundation of China （Grant No.51178226） and Basic Public Welfare Research Project of Zhejiang Province （No. LGF18E080008）.

References：

[1] MALHOTRA H L， STEVENS R F. Fire resistance of encased steel stanchions [J]. Proceedings of the Institution of Civil Engineers， 1964， 27（1）： 77-98.

[2] HUANG Z F， TAN K H， PHNG G H. Axial restraint effects on the fire resistance of composite columns encasing I-section steel [J]. Journal of Constructional Steel Research， 2007， 63（4）： 437-447.

[3] HUANG Z F， TAN K H， TOH W S， et al. Fire resistance of composite columns with embedded I-section steel： Effects of section size and load level [J]. Journal of Constructional Steel Research， 2008， 64（3）： 312-325.

[4] YOUNG B， ELLOBODY E. Performance of axially restrained concrete encased steel composite columns at elevated temperatures [J]. Engineering Structures， 2011， 33（1）： 245-254.

[5] MOURA CORREIA A J P， RODRIGUES J P C. Fire resistance of partially encased steel columns with restrained thermal elongation [J]. Journal of Constructional Steel Research， 2011， 67（4）： 593-601.

[6] HAN L H， TAN Q H， SONG T Y. Fire performance of steel reinforced concrete columns [J]. Journal of Structural Engineering， 2015， 141（4）： 04014128.

[7] WANG W Y， SONG K Y， LIU J P. Fire performance of circular tubed steel reinforced concrete columns [J]. Journal of Civil， Architectural & Environmental Engineering， 2017， 39（3）： 58-66.

[8] HAN L H， TAN Q H， SONG T Y. Fire performance of steel reinforced concrete （SRC） structures [J]. Procedia Engineering， 2013， 62： 46-55.

[9] TAO Z， YU Q. Residual bond strength in steel reinforced concrete columns after fire exposure [J]. Fire Safety Journal， 2012， 53： 19-27.

[10] LI J H， QIU D L， YU K， et al. Study on bond-slip behavior between shaped steel and concrete in SRC structures after exposed to high temperature [J]. Engineering Mechanics， 2015， 32（2）： 190-200， 206.

[11] DU E F， SHU G P， MAO X Y. Analytical behavior of eccentrically loaded concrete encased steel columns subjected to standard fire including cooling phase [J]. International Journal of Steel Structures， 2013， 13（1）： 129-140.

[12] WANG G Y， ZHANG D M， ZHENG C C， et al. Post fire performance of steel reinforced concrete columns subjected to fire including cooling phase [J]. Journal of Building Structures， 2016， 37（3）： 44-50.

[13] HAN L H， ZHOU K， TAN Q H， et al. Performance of steel reinforced concrete columns after exposure to fire： Numerical analysis and application [J]. Engineering Structures， 2020， 211： 110421.

[14] WANG G Y， XIE F D， ZHANG D M， et al. Test and parametric analysis on post-fire seismic performance of steel reinforced concrete columns [J]. China Civil Engineering Journal， 2015， 48（7）： 60-70.

[15] SHI B L，WANG G Y，MAO X Y. Experimental research on seismic performance of steel reinforced concrete column after exposure to fire [J]. Journal of Building Structures， 2017， 38（5）： 117-127.

[16] LI J H， CHEN J H， SUN B. Experimental study on the seismic performance of steel reinforced concrete columns after exposure to fire [J]. Journal of Building Structures， 2015， 36（5）： 124-132.

[17] SONG T Y， HAN L H， TAO Z. Structural behavior of SRC beam-to-column joints subjected to simulated fire including cooling phase [J]. Journal of Structural Engineering， 2015， 141（9）： 04014234.

[18] ZHANG C， XUE S D， WANG G Y， et al. Experimental research and analysis on the post-fire performance of steel reinforced concrete frame structures [J]. Engineering Mechanics， 2018， 35（5）： 152-161.

[19] LI J H， ZHANG L， GU J F ， et al. Experimental study on seismic performance of SRC frame after exposure to fire [J]. Journal of Building Structures， 2020， 41（8）： 47-56.

[20] WANG G Y， ZHANG C， Li Y， et al. Post-fire seismic performance of steel reinforced concrete frame structures [J]. Journal of Building Structures， 2017， 38（12）： 78-87.

[21] WANG G Y， SUN X， ZHAO W， et al. A finite element analysis model for post-fire seismic performance of steel reinforced concrete frame structures [J]. Journal of Building Structures， 2020， 41（4）： 92-101.

[22] WANG G Y， ZHANG C， XU J， et al. Post-fire seismic performance of SRC beam to SRC column frames [J]. Structures， 2020， 25： 323-334.

[23] LI L Z， LIU X， YU J T， et al. Experimental study on seismic performance of post-fire reinforced concrete frames [J]. Engineering Structures， 2019， 179： 161-173.

[24] Code for Seismic Design of Buildings： GB 50011-2010 [S]. Beijing： China Architecture & Building Press， 2016.

[25] DIAO B， LI S C， YE Y H. Analysis and experiment of cumulated damage of RC structures with special columns under cyclic loading [J]. Journal of Building Structures， 2008， 29（1）： 57-63.

（編辑 章润红）