应力状态和应变率对Q690钢延性断裂行为的影响
2021-03-11董俊宏沙佳阿里阿里杨波丁浩敏
董俊宏 沙佳阿里阿里 杨波 丁浩敏


摘 要:研究了中國Q690高强度结构钢在不同低应变率下的真实应力应变关系和延性断裂特征。加载了3种不同开口尺寸的单轴拉伸平板试件和纯剪试件,获得了广泛的应力状态。用试验结合数值模拟的方法确定等效塑性断裂应变、应力三轴度和罗德参数。结果表明,应力三轴度和罗德参数是控制断裂的主要影响因素。与应力相比,应变对应变率更为敏感,等效塑性断裂应变随应变率的增大而增大。此外,由于断裂前纯剪试件标距范围发生明显的变形和应力集中现象,断裂面以拉应力或拉剪应力为主,纯剪试件的设计需要进一步研究。
关键词:高强度结构钢;延性断裂;应力三轴度;罗德参数;应变率
1 Introduction
Due to the growing demand for the greater safety and lighter weight of structures, high-strength steel, such as the Chinese Q690 steel, is increasingly utilized in steel structures.
A fracture in a member of steel buildings could lead to a reduction in the member's loading capacity, and consequently a structural failure could occur. Many studies have investigated the ductile fracture mechanism of steel structures. Researchers have carried out various experimental and numerical studies about the fracture behavior of steel that investigated ductile fractures and damage.
In many studies, the stress triaxiality and the Lode parameter have been found to be the key parameters governing the ductile fracture of metallic materials. Deole et al.[1] conducted a series of metal fracture tests including tension and shear tests. A fracture locus was built, based on the stress triaxiality and the Lode parameter. They mentioned that the fracture locus depended on the calibration method used. Inspired by the mechanism of nucleation, growth and coalescence of voids, Lou et al.[2-4] developed a ductile fracture model for sheet specimens and extended it to incorporate the stress triaxiality and the Lode parameter. A changeable stress triaxiality cutoff value was also proposed, considering the various microstructures of different metals. Li et al.[5] fully investigated the ductile fracture characteristics of Chinese Q460 high strength structural steel under a quasi-static condition by using mechanical tests of four types of notched specimens. The influence of the stress state on the fracture mechanism of the material was then studied by observing the fracture surfaces of all test specimens using a Scanning Electron Microscope (SEM). Different fracture mechanisms were noticed in different stress triaxiality regions. Bai and Wierzbicki[6] found that ductile fracture was inherently a three-dimensional phenomenon and should be represented in the three-dimensional (3-D) space consisting of the stress triaxiality, the Lode parameter and the equivalent plastic strain to fracture. Sixteen fracture models were evaluated in this 3-D space.
Other studies have also revealed that the strain rate can affect metal fracture behavior. Song et al.[7] studied the effect of strain rate on the fracture behavior of low-alloy structural carbon steel by investigating monotonic tensile fractures and in-plane shear fractures under different strain rates in a quasi-static loading range. The results showed that the strain rate slightly magnified the equivalent plastic fracture strain. Sjberg et al.[8] presented a methodology for fracture characterization at strain rates up to 1 000/s, at temperatures up to 650 ℃. A high-speed camera combined with digital image correlation was used to evaluate the strain at the fracture. A coupled relationship between the temperature and the stress triaxiality controlling the fracture strain was noticed. Roth and Mohr[9] carried out low, intermediate and high strain rate tensile experiments on flat, smooth, notched and central-hole specimens extracted from high strength steel sheets; an empirical modified Hosford-Coulomb fracture model was proposed and successfully validated. Khan and Liu[10] developed an isotropic ductile fracture criterion based on the magnitude of the stress vector (MSV) to include strain rate and temperature dependences. In this criterion, an exponential term was incorporated to simulate the strain rate's effect on the ductile fracture of an alloy.No.1 DONG Junhong,et al.:Stress state and strain rate dependent ductile fracture behavior of Q690 steelIn this study, uniaxial tension and pure shear tests were performed to investigate the stress state and strain rate dependent ductile behavior of Q690 high strength steel.One unnotched steel specimen and two steel specimens with different geometrical notches were used to conduct the uniaxial tests. Pure shear sheet specimens were adopted for the shear tests. The influence of quasi-static strain rate on the material constitutive model and fracture mechanism was studied. The experimental and numerical results indicated that the shape of pure shear specimens should be enhanced to ensure that fracture happens under the pure shear stress state.
2 Experimental program
2.1 Specimen design
The layout of tensile and pure sheet specimens is illustrated in Fig.1. The tensile specimens include both notched and unnotched tensile sheets; all the sheets were fabricated from a structural steel beam with a nominal yielding strength of 690 MPa. Three samples were tested for each specimen to ensure the reliability of the data. Notch radii of R=2 mm and R=5 mm were used to obtain the results of different stress states; analogous notch radii data can be found in Reference [1] and [4]. The pure shear sheet specimen developed by Bao and Wierzbicki[11] was used in this study. Some modifications (e.g. a smooth arc radius of 5 mm at the gauge area) were made to avoid stress concentration, as depicted in Fig.1(d).
2.2 Instrumentation
The tensile and shear tests were performed using a universal testing machine (CMT5105), as shown in Fig.2. The force-displacement curve obtained directly from this machine was unreliable due to the possible slip between the clip and the specimen. Therefore, an extensometer was applied to measure the axial deformation in the gauge area until the specimen fractured. Two different quasi-static strain rates (0.000 1 and 0.01) were chosen. In order to achieve the expected strain rates, the loading rates of the universal testing machine were adjusted to 0.048 mm/min and 4.8 mm/min, respectively. All loading rates were kept constant during the entire test process. Also, a high-speed camera (VIC3D) was used to record the crack evolution of the external surface of the gauge area of the specimens.
3 Finite element model (FEM)
3.1 Material properties
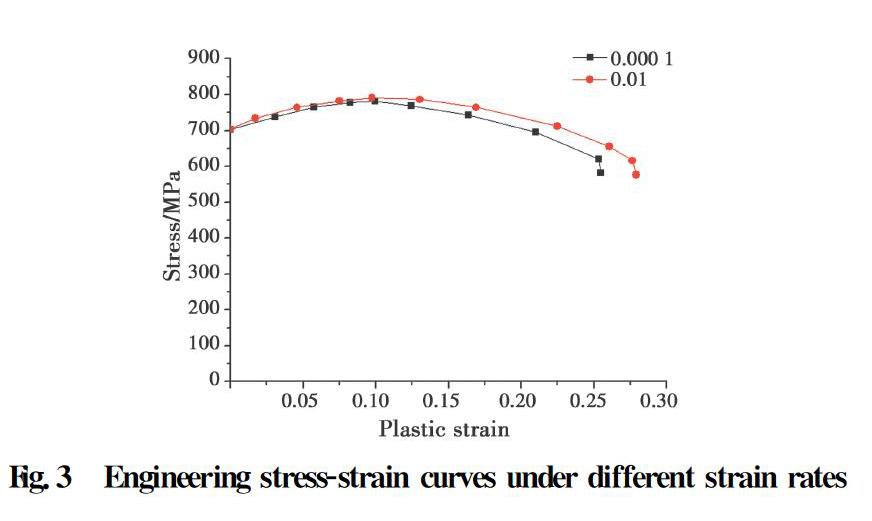
The unnotched tensile specimen (R0) was tested to determine the engineering stress-strain curves shown in Fig.3. The engineering stress is equal to the axial force divided by the initial area of the cross-section at the gauge area, whereas the engineering strain is equal to the axial elongation divided by the original gauge length. The specimens were cut using an accurate cutting machine (Dk7740). The dimension measurement showed that the error was no more than 0.2%. These curves were then converted to true stress-strain curves before necking occurred using Eq. (1) and Eq. (2).
where σtrue is the true stress,εtrue is the true strain,σ is the engineering stress, and ε is the engineering strain.
Previous studies have demonstrated that the hardening behavior of steel is significantly influenced by the strain rate. Similar work can be found in Reference[9] and [12]. One of the most famous metal hardening laws is the Johnson-Cook (JC) model[13], as shown in Eq. (3). The strain term of the JC model is always incorporated as a multiplied term in other hardening laws to include the effect of the strain rate[9].
Another commonly-used hardening law is the Swift law[14], which was used in Reference [1] and [7] for sheet specimens. In this study, the strain rate of the JC model was included in the Swift law. The true stress-strain relationship from yielding to necking was fitted with the modified Swift hardening law as shown in Eq. (4).
where D is a material parameter, m is the strain hardening exponent,ε0 is the first yield strain,εp is the plastic strain, εp· is the plastic strain rate, and ε*p· is the reference plastic rate. For the steel material used in this investigation, D=1 037.53 MPa, m=0.09 and C=0.002, which were obtained from numerical fitting of the measured data.
3.2 Solid model
The finite element software, Abaqus, was utilized to simulate the force-displacement curves. In order to save computational time and simplify the modelling process, only one eighth of the geometry of the tensile specimens (R0, R2 and R5) and half of the pure shear specimens (PS) were modelled due to the symmetrical deformation. The FEMs of the R0 and PS are illustrated in Fig.4 as the representative examples.
A mesh dependency assessment was performed. Different element sizes were evaluated in terms of computational time and accuracy. The numerical results showed that a fine element size of 0.2 mm at the gauge area was reasonably appropriate for all the specimens. The reduced integration 8-node brick element (C3D8R) was chosen to mesh the specimens, and the implicit dynamic method was used.
4 Results and discussion
4.1 Fracture mode
The experimental results of the fractured specimens showed that the macroscopic fracture morphology of the specimens was almost unaffected by the strain rate. Fig.5 shows the typical fracture modes of the R0, R2, R5 and PS specimens. Figs. 5 (a), (c), (e) and (g) were captured by the high-speed camera. A scanning electron microscope was used to obtain images of the fracture surface for these four types of specimens, as shown in Figs. 5(b), (d), (f) and (h).
The R0 specimen fractured in the form of an inclined plane, because it was difficult to ensure the verticality of the specimen parallel to the load direction. The cracks initially appeared on the outer surface of the middle part of the specimen, as recorded by the high-speed video camera. In the R5 specimen, a horizontal fracture surface was observed, and cracks also began to appear in the middle part of the specimen. The fracture surface of the R2 specimen was a horizontal plane with the cracks initiating from the root of the notch, which was mainly attributed to the stress concentration by the smaller notch radius. In Figs. 5(b), (d), (f) and (h), we can see that all the fracture surfaces in the tensile specimens were comparatively rough and consistent with the micro-fracture mechanism of nucleation, growth and coalescence of voids. However, the pure shear specimen showed a smoother fracture surface characterized by shear decohesion.
4.2 Determination of equivalent plastic strain and stress state at fracture
The numerical results are displayed in Fig.6. It can clearly be seen that there is a difference between the force-displacement curves of the tensile specimens depicted in Figs. 6(a), (b) and (c) and the pure shear specimen's force-displacement curves in Fig.6(d). As for the uniaxial tensile specimens, there was a pronounced material softening behavior before the fracture. Also, different notch radii produced distinct elongations, and a minor notch radius resulted in less elongation. In contrast to the tensile specimens, the pure shear specimen did not experience a material softening process before a fracture, which meant that fracture occurred almost when the critical shear load was reached.
In steel, the stress triaxiality and the Lode parameter are two key parameters that control the steel's fracture behavior. The stress triaxiality is defined by the ratio of the hydrostatic pressure to the Von Mises equivalent stress, as expressed in Eq. (5).
The Lode parameter was calculated by using Eq. (6).
where σ1,σ2,σ3 are the first, the second and the third principal stress, respectively.
A hybrid experiment-simulation approach was used to determine the equivalent plastic strain, the stress triaxiality and the Lode parameter at each fracture. It is generally assumed that a fracture initiates when the force-displacement curve drops abruptly. It is worth noting that due to the discreteness of the test conditions, three specimens of the same type fractured at different displacements. The points where the experimental force-displacement curves in Fig.6 drop abruptly are known as the average fracture displacement. The maximum sample variance of the fracture displacement was 0.1, which indicates the good repeatability of all test results. Subsequently, the equivalent plastic strain, the stress triaxiality and the Lode parameter were calculated from the first element expected to be deleted in the finite element model at fracture.
The first element expected to be deleted from the FEM is the hypothetical initial fracture point of the specimen. The determination of the hypothetical initial fracture point is mainly based on experimental crack evolution and the parameters related to the fracture (the equivalent plastic strain, the stress states). The location of this point is clear for the tensile specimens (R0, R2 and R5). Taking R0 as an example, it can be seen from Fig.5(a) that cracks initiated first in the middle part, meaning that the hypothetical initial fracture point was likely to lie at the center of the cross-section. Fig.7 shows the nephograms of the fracture-related parameters, such as the equivalent plastic strain, the maximum principal stress, the second principal stress and the minimal principal stress. For R0, the central element of the cross-section shows the maximum equivalent plastic strain and is most likely to be deleted first. At the same time, this part has the most unfavorable stress state, where the stress triaxiality is highest based on the three principal stresses, shown in Figs. 7(b), (c) and (d). As a result, it can reasonably be assumed that the initial fracture point of R0 is located at the center of the cross-section. The determination of the points for R2 and R5 follow the same principles. The hypothetical initial fracture point is located at the root of notch for R2, whereas it is at the center for R5.
In terms of the stress state, it is clear from Table 1 that the influence of the strain rate on the stress triaxiality and the Lode parameter was negligible in the R2, R5 and PS specimens, where the stress triaxiality and the Lode parameter remained almost constant. However, there are some variations of the stress state in the R0 specimens under different strain rates. As for the equivalent plastic strain to fracture, it should be noted that the equivalent plastic strain to fracture slightly increases with the rise of strain rate for the tensile specimens, except R5. The small variation may be due to the slight change in the strain rate. Besides, the equivalent plastic strain at the fracture of the PS remained almost unchanged. Therefore, it can be concluded that the equivalent plastic strain to fracture is influenced by strain rate for tensile specimens. The reason why the fracture strain stays constant in the PS specimens could be that there are two different microstructure fracture mechanisms. The fracture behavior for tensile specimens is characterized by the nucleation, growth and coalescence of voids, while it is believed that shear decohesion is responsible for fractures in pure shear tests.
4.4 Influence of PS specimen design on the stress state
There are two geometrical defects, that caused the tensile stress on the failure surface of the pure shear specimen. The shear failure surface is expected to be parallel to the external force. However, due to the metal's ductility, a slant failure plane was obtained in most of the pure shear tests[6, 8, 15], where the shear-tensile stress or tension stress dominates rather than the pure shear stress. The deformation history of the PS specimen used in this study is shown in Fig.9; it shows that the PS specimen failed on an inclined plane rather than a horizontal plane.
Another defect was the stress concentration caused by sudden changes of geometry in that gauge area that impeded the determination of fracture initiation. The pure shear test is used to determine the equivalent plastic fracture strain, stress triaxiality and the Lode parameter in pure shear stress state. However, the cracks started at the point where the shape suddenly changed, as shown in Fig.5(g). This indicates that the fracture was caused by stress concentration instead of the pure shear stress. The assumption that fracture occurs at the center of a cross-section, as previously adopted in many studies, is inappropriate because the fracture practically initiated at the edge points first according to the experimental results. Devising a method for determining the hypothetical initial fracture point of the PS deserves further study.
In order to avoid the inclined fracture section and stress concentration, which usually lead to a non-pure shear stress state at the fracture point, the gauge area of the PS specimen should be designed carefully. Mohr and Henn[16] recommended using butterfly specimens to avoid the edge effect by using a smooth arc, as shown in Fig.9(a), so stress concentration could be weakened in this way; but this would lead to the slant failure plane as mentioned above. A short and wide gauge area tends to keep a fracture section horizontal. Consequently, the height of the gauge area that is perpendicular to the shear load should be lower. At the same time, a minor smooth arc radius is recommended for the design of gauge area.
5 Conclusions
Sheet specimens with different geometrical notches were loaded until fractures occurred to gain data about a wide range of stress states. Two quasi-static loading rates were selected. The effects of stress state and strain rate on the constitutive material and fracture behavior of Chinese Q690 structural steel was investigated. The main conclusions can be summarized as follows:
1) The effect of the strain rate in the quasi-static range on the stress triaxiality and the Lode parameter can be disregarded.
2) The equivalent plastic strain to fracture for the tensile specimen is affected by the strain rate. Usually, a high strain rate leads to a high equivalent plastic strain to fracture.
3) For the pure shear specimen, the equivalent plastic strain at fracture was unaffected by the strain rate.
4) The pure shear test indicates that the shape of gauge area can significantly influence the stress state and fracture initiation.
Therefore, the height of the gauge area should be restricted and a small smooth arc should be used as the edge of gauge area to avoid the slant fracture section and stress concentration.
Acknowledgements
The authors gratefully acknowledge the financial support provided by the National Natural Science Foundation of China (Grant No. 51778086).
References:
[1] DEOLE A D, BARNETT M R, WEISS M. The numerical prediction of ductile fracture of martensitic steel in roll forming [J]. International Journal of Solids and Structures, 2018, 144/145: 20-31.
[2] LOU Y S, HUH H, LIM S, et al. New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals [J]. International Journal of Solids and Structures, 2012, 49(25): 3605-3615.
[3] LOU Y S, HUH H. Extension of a shear-controlled ductile fracture model considering the stress triaxiality and the Lode parameter [J]. International Journal of Solids and Structures, 2013, 50(2): 447-455.
[4] LOU Y S, CHEN L, CLAUSMEYER T, et al. Modeling of ductile fracture from shear to balanced biaxial tension for sheet metals [J]. International Journal of Solids and Structures, 2017, 112: 169-184.
[5] LI W C, LIAO F F, ZHOU T H, et al. Ductile fracture of Q460 steel: Effects of stress triaxiality and Lode angle [J]. Journal of Constructional Steel Research, 2016, 123: 1-17.
[6] BAI Y L, WIERZBICKI T. A comparative study of three groups of ductile fracture loci in the 3D space [J]. Engineering Fracture Mechanics, 2015, 135: 147-167.
[7] SONG Q Y, HEIDARPOUR A, ZHAO X L, et al. Experimental and numerical investigation of ductile fracture of carbon steel structural components [J]. Journal of Constructional Steel Research, 2018, 145: 425-437.
[8] SJBERG T, KAJBERG J, OLDENBURG M. Fracture behaviour of Alloy 718 at high strain rates, elevated temperatures, and various stress triaxialities [J]. Engineering Fracture Mechanics, 2017, 178: 231-242.
[9] ROTH C C, MOHR D. Effect of strain rate on ductile fracture initiation in advanced high strength steel sheets: Experiments and modeling [J]. International Journal of Plasticity, 2014, 56(4): 19-44.
[10] KHAN A S, LIU H W. Strain rate and temperature dependent fracture criteria for isotropic and anisotropic metals [J]. International Journal of Plasticity, 2012, 37: 1-15.
[11] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space [J]. International Journal of Mechanical Sciences, 2004, 46(1): 81-98.
[12] VERLEYSEN P, PEIRS J. Quasi-static and high strain rate fracture behaviour of Ti6Al4V [J]. International Journal of Impact Engineering, 2017, 108: 370-388.
[13] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C] // 7th International Symposium on Ballistics, 1983: 541-547.
[14] SWIFT H W. Plastic instability under plane stress [J]. Journal of the Mechanics and Physics of Solids, 1952, 1(1): 1-18.
[15] SJBERG T, MARTH S, KAJBERG J, et al. Experimental characterisation of the evolution of triaxiality stress state for sheet metal materials [J]. European Journal of Mechanics-A, 2017, 66: 279-286.
[16] MOHR D, HENN S. Calibration of stress-triaxiality dependent crack formation criteria: A new hybrid experimental-numerical method [J]. Experimental Mechanics, 2007, 47(6): 805-820.
(編辑 胡英奎)
