基于EWT-分量阈值与SVD的微震信号降噪方法

谢 博 施富强 马 胜 李 锋

1 西南交通大学牵引动力国家重点实验室，成都市二环路北一段111号，610031 2 西南交通大学机械工程学院，成都市二环路北一段111号，610031 3 四川省安全科学技术研究院，成都市武科西四路18号，610000

在将微震监测技术应用于矿山边坡、地质灾害的实时在线监测和岩体稳定性安全评估[1]时，由于采集到的数据中包含大量干扰信号[2]，探究微震信号降噪方法已成为识别岩石破裂信号和准确拾取信号初至时间的关键技术之一。部分学者将经验模态分解(empirical mode decomposition，EMD)及其改进方法引入到微震信号的分析处理中[3-7]，但与其相关的降噪方法不能完全消除边界效应和模态混叠的影响。

针对低信噪比微震信号初至拾取精度低、难度大等问题，本文基于经验小波变换(empirical wavelet transform,EWT)方法[8-9]，提出一种EWT结合分量阈值重构规则及奇异值分解技术的微震信号降噪方法，并通过仿真信号与实际微震信号验证本文降噪方法的有效性和适用性。

1 方法与原理

1.1 经验小波理论

EWT是Gilles[10]提出的一种构建自适应小波的新方法，其与EMD的相同之处是都能根据信号特点自适应调整相关参数，但EMD方法在理论基础方面有所欠缺，而小波变换方法无法自适应划分频带。因此，EWT是一种EMD自适应性与小波框架理论多尺度特点相结合的信号分析方法，具体分解过程与原理见文献[11]。

1.2 降噪算法流程

利用MATLAB软件编程，构建微震信号降噪处理算法模型，具体流程如下：

1)选取合适的小波函数，利用EWT算法将原始微震信号f(j)自适应分解为各个频率尺度的固有模态分量C0，C1，…，Ci。

2)计算原始微震信号f(j)与分解出的固有模态分量Ci的相关系数及方差贡献率。

3)对于高信噪比信号，选取相关系数大于0.3且方差贡献率大于15%的固有模态分量作为EWT分量阈值重构规则进行信号重构；对于低信噪比信号，利用SVD技术去除分量阈值重构规则未能除去的高频分量中的噪声，并与EWT计算出的低频有效分量进行重构，计算重构信号的信噪比。若信噪比无明显改善，则需返回步骤1)重新选取小波函数，再重复以上步骤。

2 仿真信号分析

利用式(1)生成能量随时间呈指数衰减的正弦信号作为有效信号，并叠加不同能量的白噪声n(t)，构造不同信噪比的仿真信号，结果见图1(a)～(c)：

x(t)=0.3e(-0.007 5t+2.25)sin(0.05πt-15π)+n(t)

(1)

首先利用EWT方法分解原始信号，并按阈值重构规则对各仿真信号进行降噪，结果如图1(d)～(f)所示。该降噪方法虽可改善原始信号的信噪比，但从各降噪信号的频谱(图2)中可以看出，与高信噪比信号(图2(c))相比，降噪后信号(图2(a)、(b))仍包含高频噪声，原因为EWT方法分解出的高频分量未能被去除。

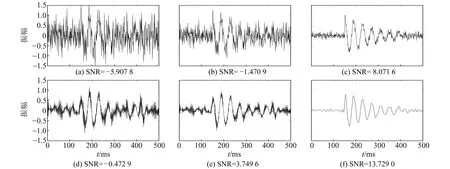
图1 仿真信号与降噪结果Fig.1 Simulation signal and denoising results

针对上述问题，本文构造EWT-SVD信号降噪方法。以图2(a)信号为例，对包含噪声的第11、12阶高频分量进行奇异值分解，得到各分量的奇异值分布如图3所示。由图可知，第11阶分量的奇异值具有“台阶”形式，选取前2个奇异值分量并通过奇异值分解逆过程进行重构，得到降噪处理的第11阶分量。而第12阶分量的奇异值不具有“台阶”形式，认为该分量主要由噪声信号贡献，可去除该分量。将降噪后的第11阶分量与满足分量阈值重构条件的其他低频EWT分量进行重构，得到降噪信号(图4(a))，图4(b)信号同样按上述步骤完成降噪。对比图2和图4发现，高频部分对应的幅值可得到有效抑制，且降噪信号的信噪比分别升至3.956 7和7.803 0。

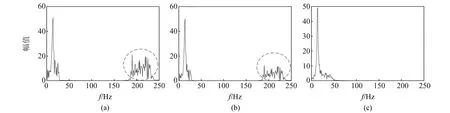
图2 降噪信号频谱Fig.2 Denoising signal spectrum

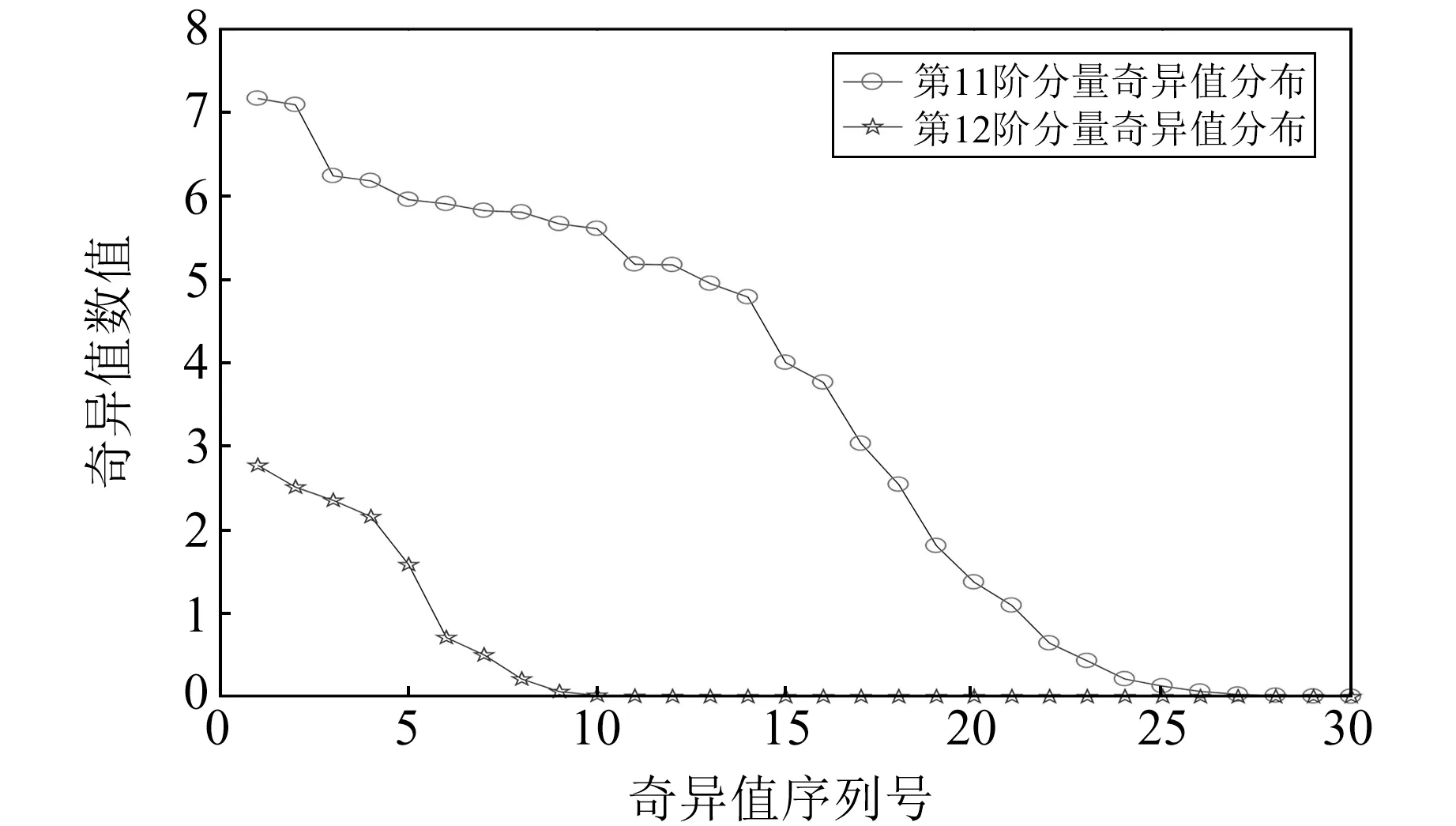
图3 第11、12阶分量奇异值分布Fig.3 The singular value distribution of 11th and 12th order components

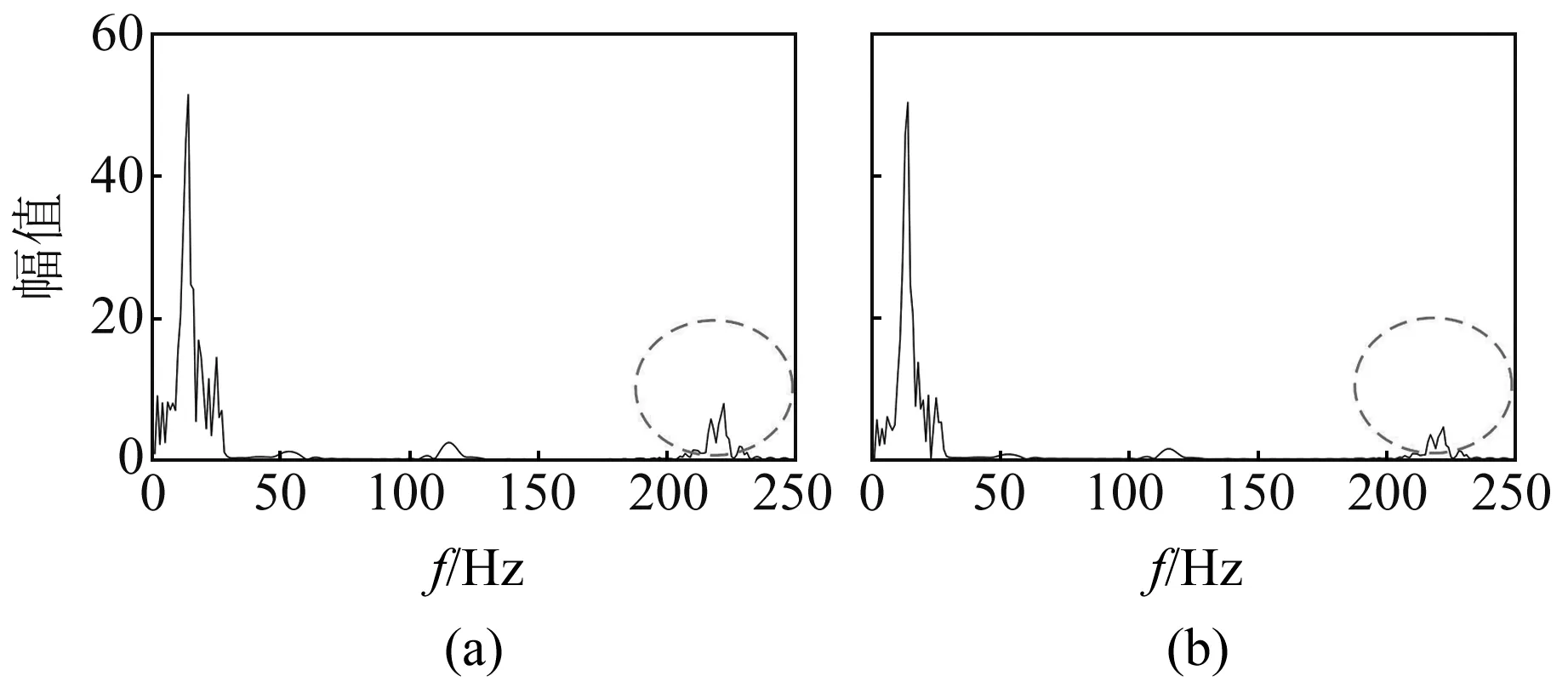
图4 低信噪比信号EWT-SVD降噪频谱Fig.4 EWT-SVD denoising spectrum of low signal-to-noise ratio signal

3 实例应用分析

截取一段微震信号，其时域图与频谱图分别如图5(a)和5(b)所示，微震信号的有效成分被噪声掩盖，且信号中混杂着不同频率的噪声信号，很难直接读取到微震信号的初至时间。利用本文提出的降噪方法分析该信号并拾取信号初至，进一步验证本文方法的适用性。

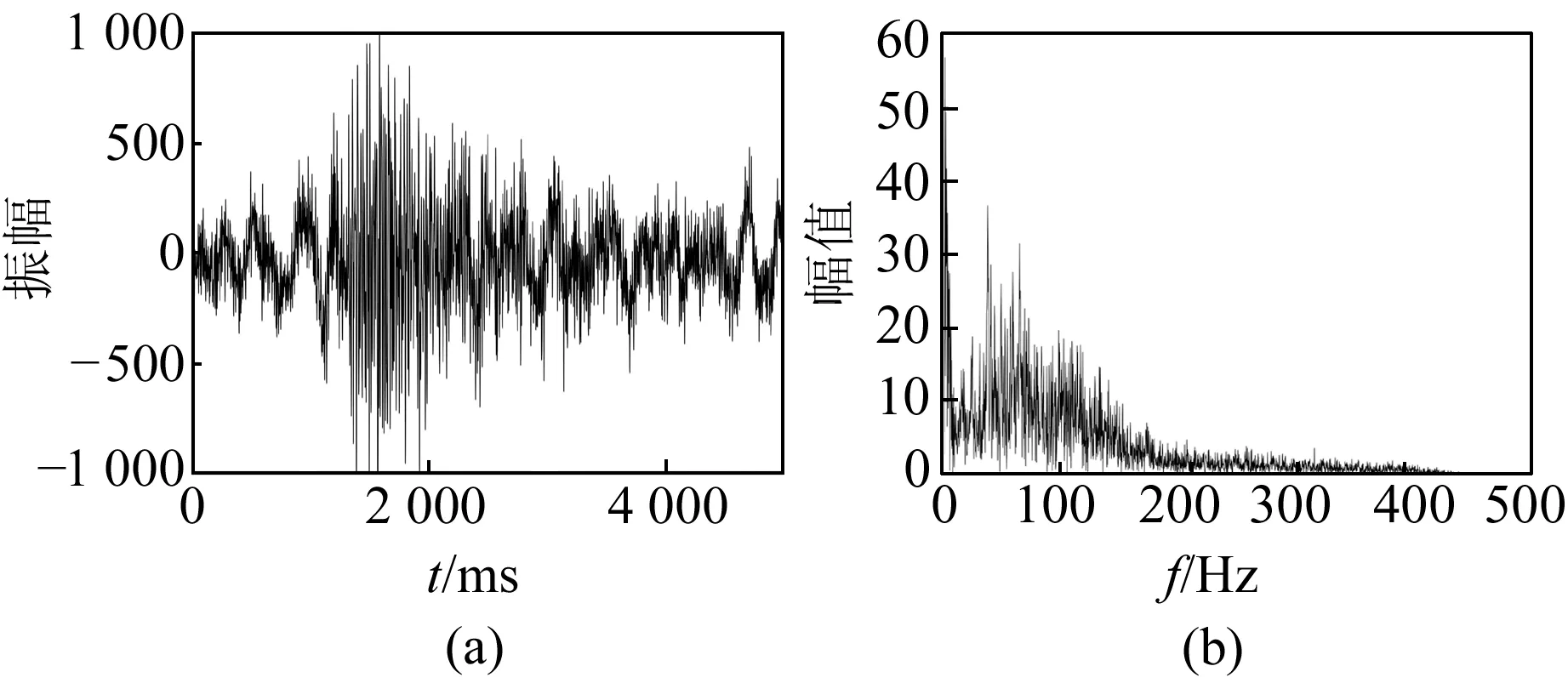
图5 原始信号及其频谱Fig.5 Original signal and its spectrum

EWT方法分解的微震信号中，第1、4和6阶分量满足分量阈值重构条件，但由于第4和6阶分量中噪声信号贡献的频率占比较大，对其采用奇异值分解进行降噪，并与第1阶分量进行重构，得到的降噪结果如图6所示。从图中可以看出，与原始微震信号相比，降噪后的信噪比得到明显改善。从频谱图中可以看出，分解的微震信号中第1阶低频有效成分得以保留，但有效频率成分中仍包含部分噪声成分的第4和6阶分量，通过SVD降噪后所在频段的幅值均有所降低，其余由噪声贡献较多的频段则被完全去除。另外，利用修改的能量比(modified energy ratio，MER)法[12]和分形维数(fractal dimension，FD)法[13]拾取的初至时间分别为1 155 ms和1 150 ms(图7)，与实际到时1 146 ms相比，相对误差分别为0.79%和0.35%，表明经EWT-SVD降噪后信号的初至特征更加明显，验证了本文降噪方法的有效性。

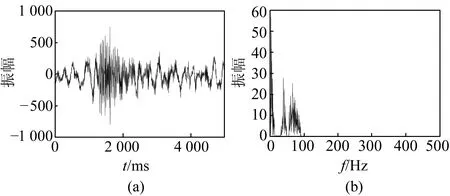
图6 降噪信号及其频谱Fig.6 Denoising signal and its spectrum

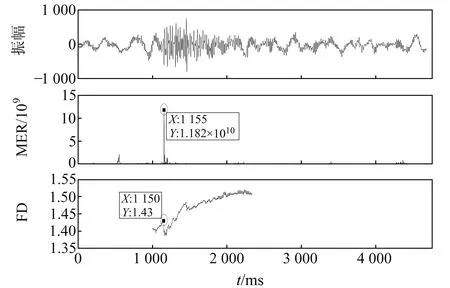
图7 降噪信号的初至拾取结果Fig.7 Primary arrival picking results of denoising signal

4 结 语

1)分量阈值重构规则能去除噪声含量高的EWT分量，采用SVD技术对其他高频分量进行降噪并与低频有效分量进行重构，能最大限度地保留原始信号中的有效信息，改善信号信噪比。

2)利用本文降噪方法对仿真信号进行降噪，对比降噪前后信号的频谱变化发现，本文方法对不同信噪比的仿真信号均有较好的降噪效果。

3)基于EWT结合分量阈值重构规则与SVD技术对实际微震信号进行降噪，不仅能改善信号的信噪比，而且能明显增强信号的初至特征，使初至精度得到提高。实验证明，本文提出的降噪方法具有有效性和适用性。