不同升温管及升温对大体积混凝土边界影响模拟分析
2021-03-11吴玉华
丘 弋,吴玉华
(1、广东省建科建筑设计院有限公司 广州510010;2、广东省工业设备安装有限公司 广州510220)
0 引言
在地下工程中,墙体质量的差异将直接影响整个结构的防水性能与耐久性[1]。若混凝土产生初始裂缝,不仅修复困难且成本极高,更难以恢复至未产生裂缝前的结构初始状态。因此,预防和控制裂缝远远重要于裂缝产生后的修复[2]。
由于浇筑时间不同,导致混凝土侧墙与底板收缩不一致,混凝土墙体相对底板收缩量大,因此受到底板的约束作用,从而使混凝土侧墙内部产生拉应力。浇筑时间相差越久,约束越强,混凝土侧墙内部拉应力越大。若拉应力超过混凝土的抗拉强度,墙体就会出现垂直于底板的裂缝[3-4]。通过深入分析,发现侧墙产生裂缝的原因为侧墙与底板的收缩不一致,提出物理加温和降温的处理措施,从而减少和避免裂缝的产生[5-7]。
因此,本文针对混凝土底板采用不同升温管的布置方式,对其进行升温处理,探究不同升温边界的变化及其混凝土收缩/膨胀性能的响应过程。
1 模型简化处理及其准确性验证
1.1 模型的选取
本文以某航站楼主体围护结构地下连续墙为例(见图1),进行分析。模型中底板及侧墙均采用C35混凝土,与底板接触的基础层为回填土,整个地下结构宽为54.5 m,长为310.175 m。
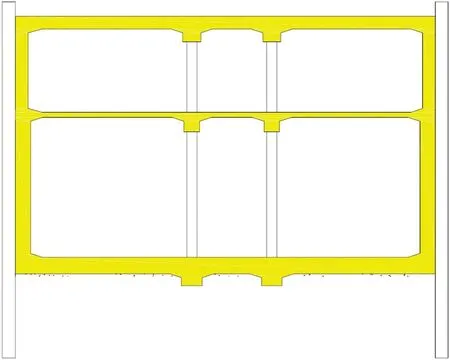
图1 地下底板及侧墙示意图Fig.1 Configuration of Underground Floor and Side Wall
1.2 模型的简化处理
考虑实际工程呈对称结构,本文对模型进行简化处理,其过程如图2 所示。选取长度方向及宽度方向的底板混凝土进行,将实际工程简化为3.0 m×5.4 m×1.3 m 的有限元模型。基础部分统一按照回填土处理,分别取宽度4.5 m,长度方向7.9 m,厚度1.5 m。
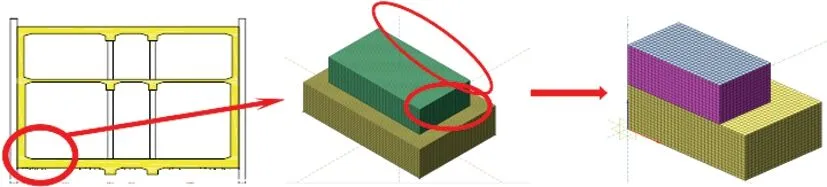
图2 模型简化Fig.2 Model Simplification
同时,考虑对混凝土进行升温处理时,仅有与侧墙接触部位的混凝土需进行重点分析,且其四周边界可近似认为一致。因此,本文将原有有限元模型简化为1/4模型,进行多参数分析。
1.3 简化模型的准确性验证
为了验证本文模型简化的准确性,通过对全模型及1/4 模型的升温过程采用MIDAS FEA 进行有限元分析[8-9]。整个模型由2部分组成,分别为混凝土底板及地面,2组模型的混凝土试件及基础尺寸,如1.2节所示。其中,将混凝土的网格尺寸划分为50 mm×50 mm×50 mm,基础网格尺寸划分为100 mm×100 mm×100 mm,2组试件的水化热分析时间均为170 h。
1.3.1 模型参数
⑴混凝土导热系数与比热
根据《大体积混凝土施工规范:GB 50496—2012》第G.0.1 条,可计算得到C35 混凝土的导热系数γ =2.625 W/(m·℃)及比热c=945.15 J·g/(N·℃)。
⑵混凝土表面热交换系数
依据气象资料,预估混凝土浇筑现场平均气温为28 ℃,浇筑现场无风,将混凝土试件与空气接触的上表面放热系数定义为18.442 2 W/(m2·K),试件四周放热系数为7.0 W/(m2·K)。
⑶混凝土最大绝热升温及导温系数
采用日本规范JSCET 2012中的混凝土绝热温升曲线,定义混凝土入模温度为28 ℃,水泥用量为251 kg/m3,对应设置混凝土的最大绝热温升43.424 ℃,导热系数为1.933。
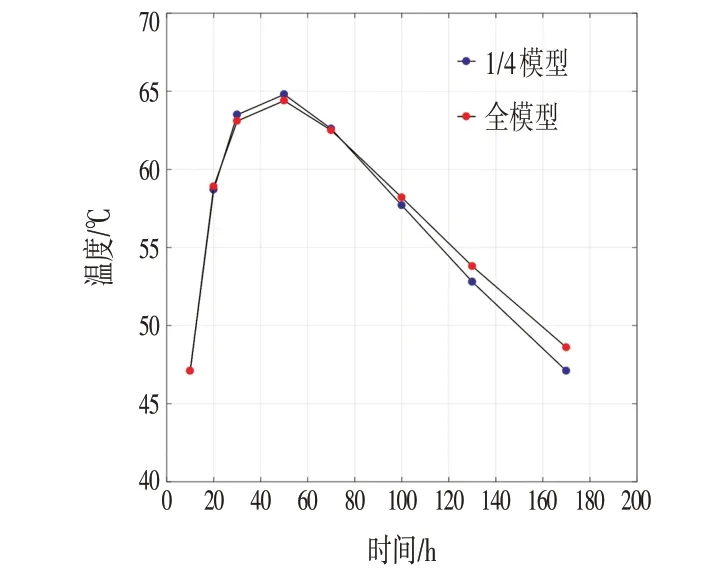
图3 全模型与1/4模型温升曲线对比Fig.3 Comparison of Temperature Rise Curves between Full Model and 1/4 Model
通过MIDAS 软件进行170 h 水化反应模拟,得到全模型与1/4模型的温升曲线,如图3所示。从图3中可知,两者温度上升及下降趋势保持一致,且达到最大温度时间一致,不同时间阶段的温差在2%以下。因此,可保证本文所建立的简化模型准确性,后续进行升温分析时,可采用简化模型进行分析。
2 不同升温参数对底板与侧墙边界的影响
2.1 升温模型的构建
通过物理升温手段来使底板混凝土凝固之后再进行膨胀,从而达到与侧墙协调变形的目的。因此,本文结合工程实例,明确侧墙与底边的3种接触边界,即长边接触、短边接触及两边均接触。依据上述接触边界,分别设置6 种升温管布置方式,即短边单排布置、长边单排布置、短边双排布置、长边双排布置、两边单排布置及两边双排布置,其布置方式如图4所示。

图4 不同升温管布置方式Fig.4 Different Arrangement of Heating Pipes
除升温管布置方式外,升温温度对混凝土的膨胀位移也有很大影响。因此,在不同升温管布置方式的基础上,设计了6 种升温温度,即80 ℃、90 ℃、100 ℃、110 ℃、120 ℃及150 ℃,探究不同升温温度对大体积混凝土不同方向膨胀位移的影响。通过对升温管及升温温度组合设计模型,共形成36个不同加温方式的有限元模型,形成12个对比分析组,具体参数如表1所示。

表1 升温边界参数Tab.1 Temperature Rise Boundary Parameter
2.2 不同升温温度对边界膨胀位移的影响
上述分析中,虽明确在一定温度条件下,不同升温管布置方式,不同方向最大膨胀位移的变化情况,但有关温度的界限,则需进一步分析。通过对不同布置方式,设置6 个升温温度,即80 ℃、90 ℃、100 ℃、110 ℃、120 ℃及150 ℃,采用MIDAS FEA 进行分析,明确不同升温布置方式适宜的使用情况。
2.2.1 升温管短边单排布置
分析结果如表2、图5 所示,当采用短边单排布置升温管时,其长边x方向的膨胀位移均小于水化反应的最大位移,表示其不适用于长边底板与侧墙存在接触条件下,进行升温膨胀控制侧墙裂缝。同时,短边x方向膨胀位移在升温温度80~110 ℃时,也小于其水化反应的最大膨胀位移。因此,当采用短边单排布置时,应采用110 ℃以上的升温温度,在短边底板与侧墙接触的条件下,控制侧墙裂缝的产生。

表2 升温管短边单排布置最大膨胀位移Tab.2 Maximum Expansion Displacement of Single Row Arrangement on Short Side of Heating Pipe

图5 短边单排布置不同升温温度膨胀位移Fig.5 Expansion Displacement of Short Side Single Row with Different Temperature Rise
2.2.2 升温管长边单排布置
其分析结果如表3 所示,当采用长边单排布置升温管时,其短边y 方向的膨胀位移均小于水化反应的最大位移,表示其不适用于短边底板与侧墙存在接触条件下,进行升温膨胀控制侧墙裂缝。同时,长边y方向膨胀位移在升温温度80~90 ℃时,也小于其水化反应的最大膨胀位移。因此,当采用长边单排布置时,应采用90 ℃以上的升温温度,在长边底板与侧墙接触的条件下,控制侧墙裂缝的产生。
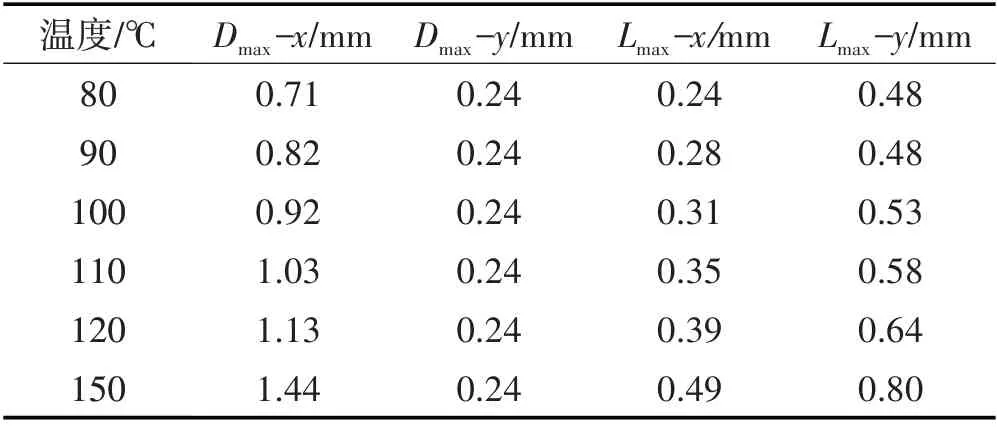
表3 升温管长边单排布置最大膨胀位移Tab.3 Maximum Expansion Displacement of Single Row Arrangement on Long Side of Heating Pipe
2.2.3 升温管短边双排布置
分析结果如表4 所示,当增加短边布置的升温管数量时,其在各个方向的最大膨胀位移略有增大,但其短边x 方向在升温温度80~110 ℃条件下,仍然小于水化反应的最大膨胀位移,而长边x 方向最大膨胀位移均小于水化反应的最大膨胀位移。结合表4中分析结果可知,短边方向的加温管数量与其最大膨胀位移存在存在相关性。因此,当控制短边底板与侧墙接触情况下的侧墙裂缝时,建议采用升高加温管温度的方式进行。

表4 升温管短边双排布置最大膨胀位移Tab.4 Maximum Expansion Displacement of Double Rows Arrangement on Short Side of Heating Pipe
2.2.4 升温管长边双排布置
分析结果如表5 所示,当采用长边双排的升温管布置方式时,其在温度大于110 ℃条件下,对长边及短边的侧墙裂缝控制,均能满足相应需求。但当温度低于110 ℃时,仅能用于长边的侧墙裂缝控制,其短边y方向的最大膨胀位移小于水化反应的最大膨胀位移,不能满足协同变形的要求。
2.2.5 升温管长边及短边单排布置
分析结果如表6 所示,当采用长边及短边同时排布单排升温的布置方式时,温度仅需大于80 ℃,其均能满足不同方向的最大膨胀位移要求。当充分考虑升温管布置时,均预埋于混凝土内,仅供一次性使用。因此,针对升温管布置方式与其成本之间进行分析,当升温膨胀较位移较大时,宜采用两边单排布置方式,控制短边、长边及两边同时的侧墙裂缝控制,而当升温膨胀位移较小时,则应选择其他方式布置。

表5 升温管长边双排布置最大膨胀位移Tab.5 Maximum Expansion Displacement of Double Rows Arrangement on Long Side of Heating Pipe

表6 升温管长边及短边单排布置膨胀位移Tab.6 Expansion Displacement of Single Row Arrangement for Long Side and Short Side of Heating Pipe
2.2.6 升温管长边及短边双排布置
从表7、图6 的有限元分析结果可知,当采用两边同时布置升温管时,其最大膨胀位移随数量增多而迅速增大。然而,混凝土的抗拉应力较小,相对应的膨胀位移也较小。因此,在进行升温管布置时,过多地布置两边升温管数量,极易造成混凝土产生裂缝。而针对不同膨胀位移要求时,可通过增加一边升温管数量,减少另一侧升温管数量的方式进行布置,从而达到控制侧墙裂缝的膨胀位移变化需求的目的。
从上述有限元分析结果总结可知,当采用升温管短边布置时,其温度的增加对膨胀位移的增长不显著,且其仅能用于短边侧墙裂缝控制。当采用升温管布置时,数量的增加能有效随着温度的升高,其膨胀位移出现显著增加,当温度大于110 ℃时,其不仅仅可用于长边侧墙裂缝控制,也可用于短边侧墙裂缝控制。而采用双边升温管的布置方式,其对温度要求较低,相较于前2 种升温管布置方式,其能在80~90 ℃的温度区间内,达到两边侧墙裂缝控制的膨胀位移要求。
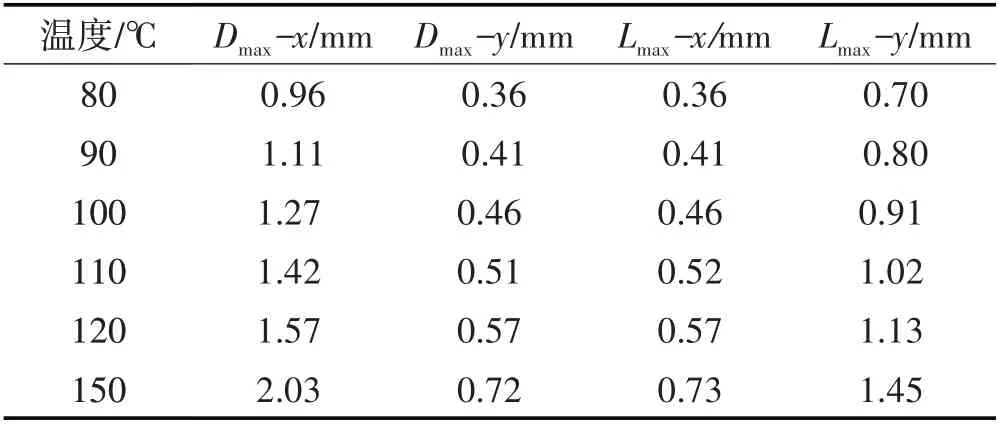
表7 升温管长边及短边双排布膨胀位移Tab.7 Double Row Expansion Displacement of Long Side and Short Side of Heating Pipe
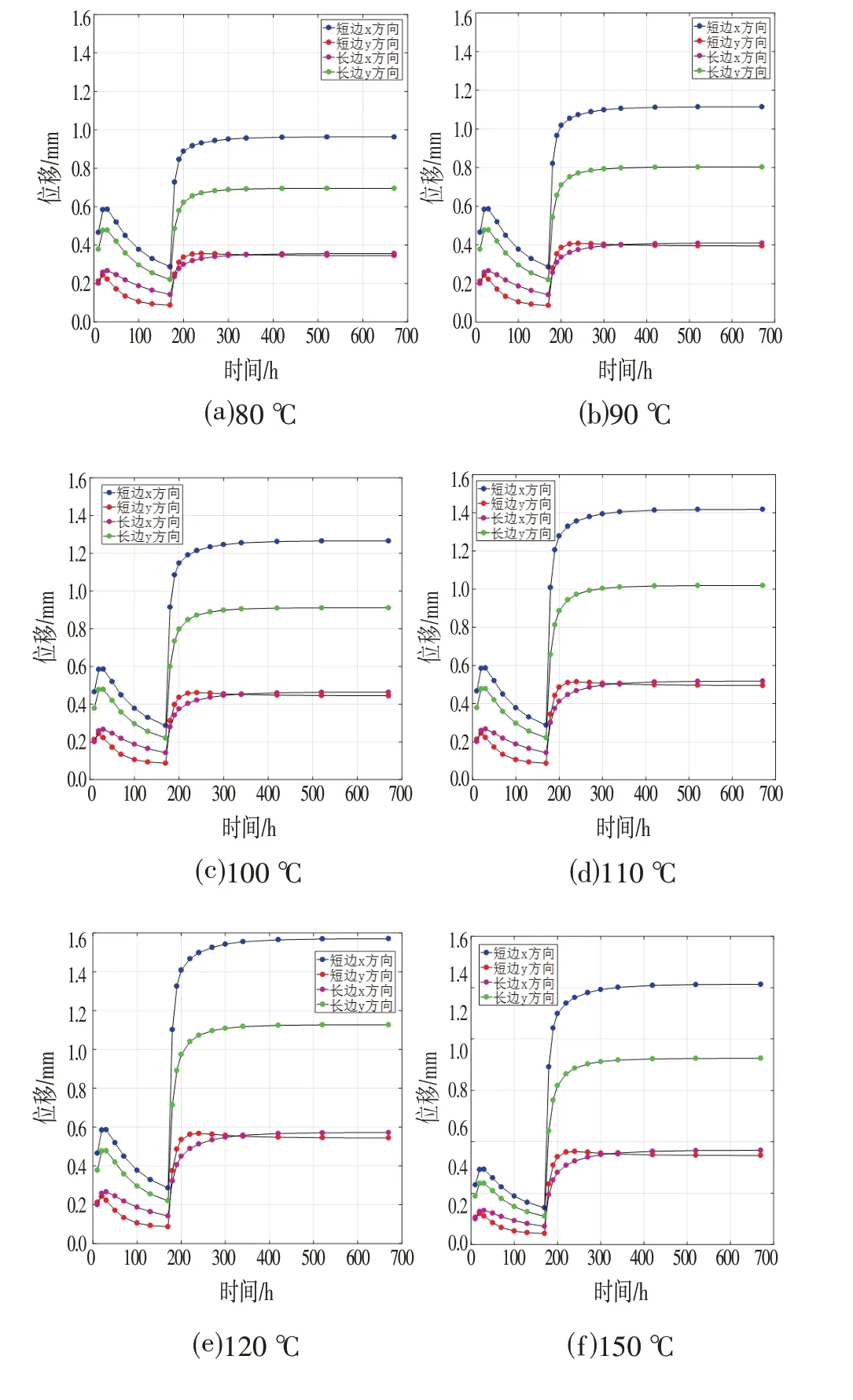
图6 两边双排布置不同升温膨胀位移Fig.6 Double Row Arrangement of Different Temperature Rise Expansion Displacement on both Sides
3 结论
本文以侧墙与底边接触情况、加温管布置数量及加温管升温温度为参数,对36 个升温模型采用MI⁃DAS FEA进行有限元分析,得到以下结论及建议:
⑴通过有限元分析结果可知,采用物理升温的方式对大体积混凝土进行膨胀,其最大膨胀位移大于水化反应产生的膨胀位移,表明可采用此种方式来控制底板膨胀,达到与侧墙协调变形的目的。
⑵增加升温管的布置数量能提升混凝土底板不同方向的膨胀位移,但当温度低于80 ℃时,其升温最大膨胀位移均小于水化反应最大膨胀位移。
⑶两边布置升温管方式相较于增多一边升温管布置数量,其对短边及长边的x 方向、y 方向位移增加更为明显。
⑷通过上述参数分析可知,在侧墙与底板的3种接触条件下,充分考虑加温管升温成本及加温管布置的成本影响。对于短边底板与侧墙接触的情况,宜采用90 ℃两边单排的加温管布置方式,对短边侧墙裂缝进行控制;对长边底板与侧墙接触的情况,宜采用80 ℃长边双排的加温管布置方式,对长边侧墙裂缝进行控制;对短边及长边底板均与侧墙接触的情况,宜采用80 ℃两边双排的加温管布置方式,对两边侧墙裂缝进行控制。
