基于概率密度演化理论的结构疲劳可靠度研究进展

唐伟

（重庆大学土木工程学院，重庆 400045）

0 引言

研究表明，疲劳损伤是引起大多数工程结构或机械主要失效原因[1]。结构疲劳损伤过程具有较强的随机性，如材料随机性和荷载随机性[2，3]。因此，可靠度方法成为评估疲劳损伤的有效手段[3]。目前，可靠度方法包括：一次二阶矩方法、蒙特卡洛法等[4-5]。一次二阶矩方法适用求解线性问题，且随机参数需满足独立正态分布[6]，具有一定的局限性。蒙特卡洛法具有直观、精确度高、不受线性和非线性影响的特点，但计算效率低[3]。

21 世纪以来，李杰、陈建兵等[7-9]学者针对随机动力系统建了概率密度演化理论，为解决实际大型工程结构的可靠性分析等提供了新的思路。外部随机激励所产生的交变荷载是引起工程结构或机械结构的疲劳损伤的主要原因，故疲劳损伤过程与结构的动力响应密不可分。基于此，将概率密度演化方法与结构的疲劳损伤相结合是未来疲劳损伤预测的一种新途径。本文将论述概率密度演化方法在结构疲劳可靠度中的相关研究进展。

1 概率密度演化理论

1.1 广义概率密度演化方程

在随机外部激励下结构的动力反应方程[8]为

其中随机参数包括：材料的变异性和外部激励的随机性。将系统所有变量可记作在整个随机过程中无随机变量的增减，因此该随机过程满足概率密度守恒原理[7，8]即

式中：ΩY×ΩΘ-联合概率空间的联合概率密度函数，对式（2）进一步推导可得

1.2 广义概率密度演化方程求解步骤

广义概率密度演化方法将物理空间与概率空间进行了解耦处理，将物理方程与概率密度演化方程联合并通过数值方法求解结构响应的概率密度演化函数。具体步骤如下[6-9]：

（1）确定影响结构响应的随机参数Θ 和分布类型，建立结构响应的状态函X 或分析模型。

（2）根据随机参数数量和分布利用数论选点理论获取随机参数样本和赋得概率Pq，将随机样本带入到结构响应的状态函数X或分析模型，获取初始条件：

式中：δ[·]-Dirac 函数；Nsel-数论选取样本数。

（3）将式（4）带入式（3），利用 TVD 差分法求解偏微分方程求出结构响应的概率密度函数：

（4）根据结构失效的极限状态方程Y=F（X），对式（6）积分，其可靠度为：

2 基于虚拟时间的疲劳可靠度概率演化方法

赵俭斌等[5]基于概率密度演化理论给出了风机基础疲劳可靠度的计算方法。该方法将风荷载视为疲劳损伤过程中的随机参数，其激励荷载如下：

式中：μD-拉力系数；ρ-空气密度；Vj-风速与随机参数θ 有关；Bj-塔身面积[5]。

利用Miner 线性疲劳累积损伤模型[10]D 构造了依赖于随机参数θ 的虚拟随机过程Zl：

式中：τ 为虚拟时间；nk和Nfk分别为第k 级应力幅实际循环次数和疲劳寿命。Zl关于 τ 的导数为 D（θ，T），在 τ=1 时的截口随机变量为D（θ，T）。故其概率密度演化方程为：

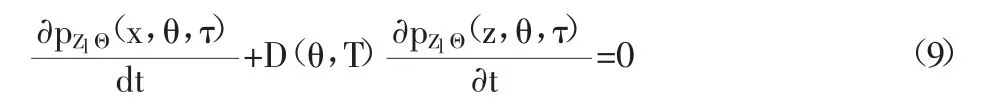
该方法充分考虑了外界激励的随机性，在求解疲劳损伤时，参考了静力结构可靠度的概率密度演化求解法，引入虚拟时间，巧妙地解决了疲劳可靠度与时间的关系。但该方法未考虑疲劳损伤过程中材料的不确定，即不同应力幅对应的疲劳寿命Nf的随机性。

3 一般形式的疲劳可靠度预测方法

徐亚洲[3]基于疲劳损伤的一般形式推导了概率密度演化方法的求解思路。该方法假定疲劳损伤模型为：

结合概率密度演化理论，可得一般形式的疲劳损伤演化偏微分方程：

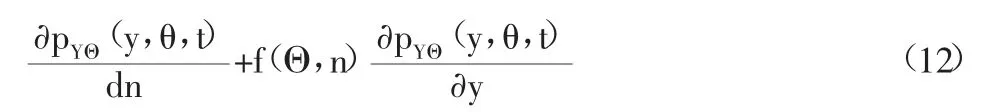
该疲劳寿命模型将应力幅和对应的疲劳寿命视为随机参数，建立了疲劳累积损伤与荷载作用次数的演化规律，充分考虑了外界激励的随机性和材料的随机性。但该方法只给了疲劳损伤的一般模型，并未给出考虑多级变幅疲劳可靠度具体方法。例如多级变幅线疲劳线性累积损伤模型为：

因该方法考虑了外界激励和材料的随机性，（13）中随机参数包括各应力幅循环次数ni和疲劳寿命Nfi，由于ni具有随机性，只知其满足而ni与荷载作用总次数n 的具体关系无法确定。当应力幅级数s 较多时，导致式（11）疲劳损伤变化率无法确定，因此利用该方法求解多级变幅疲劳可靠度难度较大。

4 基于裂纹尺寸扩展概率密度演化方法

刘勇[2]对既有的Paris 疲劳裂纹扩展确定性模型进行推导给出了随机裂纹扩展模型，给出了相应的概率密度演化方程如下：

式中：m 和C-材料裂纹扩展参数；a-表面裂纹尺寸；Y-几何修正系数；β-交变应力峰值，其他参数见文献[2]。涉及随机参数为C，m和ξ。其偏微分方程为：

该方法从材料的分散性和荷载的随机性引入了疲劳裂纹扩展速率公式，给出了疲劳裂纹扩展的概率密度演化函数的求解方法。从裂纹扩展微观角度给出了损伤演化的过程，具有较强的物理意义。但由于实际结构的裂纹往往在其内部，检测难度较大，且该方法相对较复杂，因此在实际工程运用中还需进一步研究。

5 结论与展望

上述三种方法，从不同的角度证明了概率密度演化方法在疲劳可靠度预测中具有较大的潜力，在解决线性和非线性问题上都具有较强的可行性。与经典的可靠度求解方法相比，其可靠度为时变可靠度，且该方法与数论相结合，能够巧妙的避免高维问题。

但概率密度演化方法还未被广泛适用于预测疲劳可靠度，其原因在于目前疲劳损伤累积模型较多，其复杂程度也各有差异，因此，疲劳损伤变化率求解具有一定难度，针对不同的疲劳损伤模型还需进一步研究。

通过分析以上三种方法，希望能为广大学者提供更多的疲劳可靠度思路。随着广大学者的进一步研究，此方法会更加广泛地应用于预测结构疲劳可靠度。