深度学习算法的城市轨道交通短时客流量预测

任 娜

（陕西交通职业技术学院，陕西西安 710018）

随着经济不断发展，城市交通得到迅速发展，许多城市出现了轨道交通网络系统，让人们的工作、生活更加方便。轨道交通为解决大城市的交通拥挤提供了一种新的交通工具［1］。在轨道交通的实际应用中，还存在一些问题，如轨道交通与城市发展速度不相匹配，轨道交通规划不够科学，无法使轨道交通网络系统的作用发挥到最大化［2-4］，而短时客流量可以描述城市轨道交通的运营情况，找到城市轨道交通客流量的变化趋势。因此，进行短时客流量预测和建模对轨道交通合理规划和管理具有重要的研究意义［5-6］。

影响城市轨道交通短时客流量的因素复杂，并且其具有随机性、周期性、相关性及非线性的特征，给城市轨道交通短时客流量预测建模带来一定的困难。针对城市轨道交通短时客流量预测问题，国内外一些学者进行了相关研究。最初城市轨道交通短时客流量预测基于传统统计学理论，如，基于ARIMA的城市轨道交通短时客流量预测模型［7］，其建模过程比较简单。ARIMA的城市轨道交通短时客流量预测模型，描述城市轨道交通短时客流量时变性能力不强，因此预测结果不准确［8］。随后出现了基于现代统计理论的城市轨道交通短时客流量预测模型，如，支持向量回归机、极限学习机、长短时记忆神经网络等［9-11］。这些模型具有较好的自学习能力，城市轨道交通短时客流量预测效果明显提升，而且已成为当前城市轨道交通短时客流量预测建模的主要研究方向［12］。然而在实际应用中，同样存在一定的不足，如，支持向量回归机的计算量大，预测城市轨道交通短时客流量效率低；极限学习机、长短时记忆神经网络没有考虑城市轨道交通短时客流量的混沌性，预测精度有待改善［13］。

为了获得理想的预测结果，更加准确地描述城市轨道交通短时客流量变化趋势，提出了深度学习算法的城市轨道交通短时客流量预测模型。该方法引入混沌理论构建城市轨道交通短时客流量的训练样本，并引入长短时记忆神经网络设计城市轨道交通短时客流量预测模型，在相同仿真实验环境下，与其他模型进行对比测试。结果表明，深度学习算法是一种预测精度高、结果可靠的城市轨道交通短时客流量预测模型，具有十分显著的优越性，为城市轨道交通短时客流量变化趋势跟踪提供了一种有效的建模方法。

1 相关技术

1.1 城市轨道交通短时客流量序列的混沌分析

对于城市轨道交通短时客流量数据的时间序列，当时间序列为一维时，城市轨道交通短时客流量变化特点不明显，表面上没有什么规律，为此需要对城市轨道交通短时客流量原始数据进行重构，不断拓展其维数，找到城市轨道交通短时客流量随时间变化的规律［14］。设城市轨道交通短时客流量原始数据序列为：X={x1，x2，...，xn}，n表示数据长度，设嵌入维数为m，时间延迟为τ，则经过混沌分析和处理，得到

式（1）中，M表示相空间点数，且有M=n-（-1）τ。

本文采用互信息法计算城市轨道交通短时客流量的时间延迟，用于描述城市轨道交通短时客流量的非线性变化特点，平均信息熵计算公式为

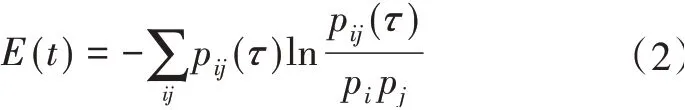
式（2）中，pi和pj表示城市轨道交通短时客流量序列区间i，j内的概率，pij(τ)表示联合概率［15］。

当平均信息熵达到第一个极小值时，表示城市轨道交通短时客流量数据之间的关联性最小，此时则得到了最优的时间延迟。

采用Cao法确定城市轨道交通短时客流量的最优嵌入维数，步骤如下：

（1）在m+1维的空间中，第i，j个状态点分别为，两点之间的欧式距离比值计算公式为

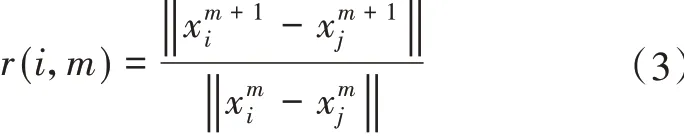
（2）计算全部欧式距离比值的平均值，具体为

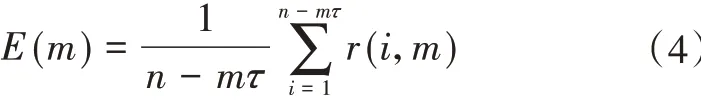
（3）计算E(m+1)和E(m)的比值Em，具体如下：

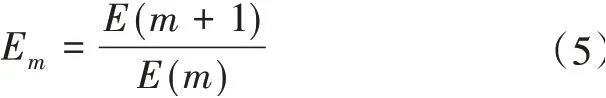
（4）不断执行步骤（1）～（3），当Em变化比较平稳时，表示此时的嵌入维数为最优。

1.2 长短时记忆神经网络

深度学习算法是近几十年才发展起来的人工智能技术，其中长短时记忆神经网络是一种最流行的深度学习算法，其利用“记忆单元”替换传统神经元，可以有效避免传统神经网络的“过拟合”现象出现。对比普通的循环神经网络，其具有长时记忆的功能，对比混沌分析和BP神经网络，长短时记忆神经网络具有更强的拟合能力。因此，本文利用长短时记忆神经网络预测城市轨道交通短时客流量。长短时记忆神经网络的基本结构如图1所示。

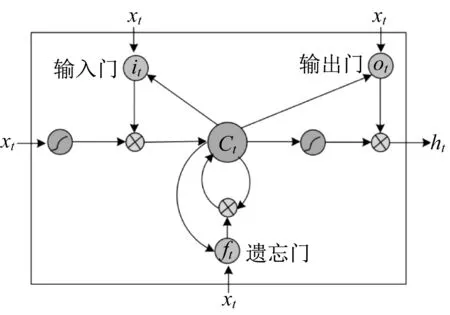
图1 长短时记忆神经网络的基本结构Fig.1 Basic structure of long-term and short-term memory neural network

长短时记忆神经网络的建模包括两个过程：前向传播过程和反向传播过程。其前向传播过程具体如下：

设在t时刻，外部的输入为xt，在时刻t-1的记忆单元、其他隐含层的状态分别为st-1和bt-1，将它们作为输入，那么在t时刻，输入门的输入和状态分别为at l和具体如下：

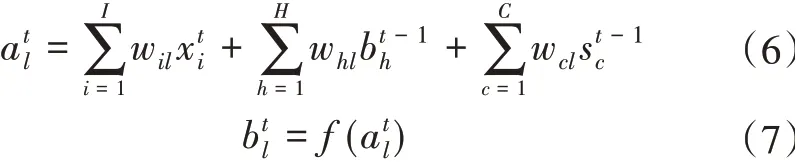
式（7）中，f（）表示激活函数，I，H，C分别表示输入层与记忆单元相连接的隐含层的神经元数量，C表示所有输入个数，wil、whl和wcl分别表示和的权值。

在t时刻，遗忘门的输入和状态分别为，计算公式分别为

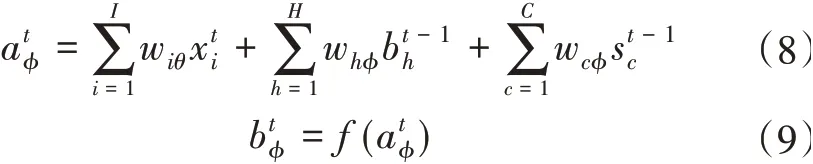
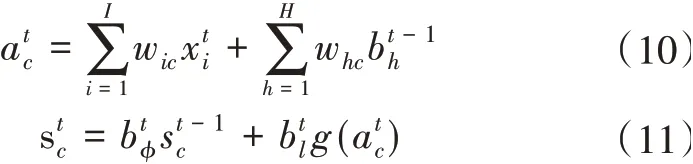
基于输入门状态的计算公式相似原理，可以得到在t时刻，输出门的输入和状态的计算公式分别为

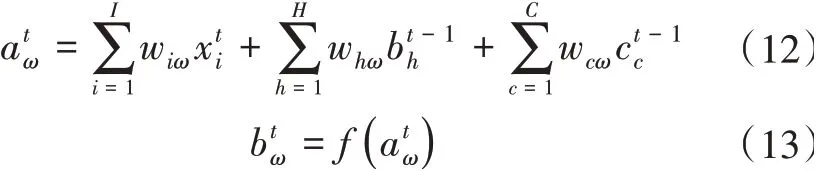
综上可知，在t时刻，长短时记忆神经网络整个输出为

长短时记忆神经网络的反向传播过程具体如下：

在t时刻，节点j、记忆单元Cell和Cell状态的残差为则输出层和记忆单元Cell输出向量的残差计算公式分别为

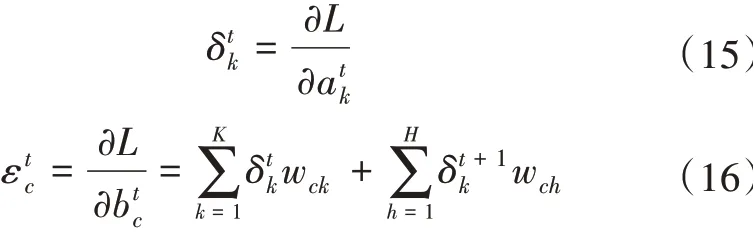
输出门、Cell单元、遗忘门、输入门的残差计算公式分别为

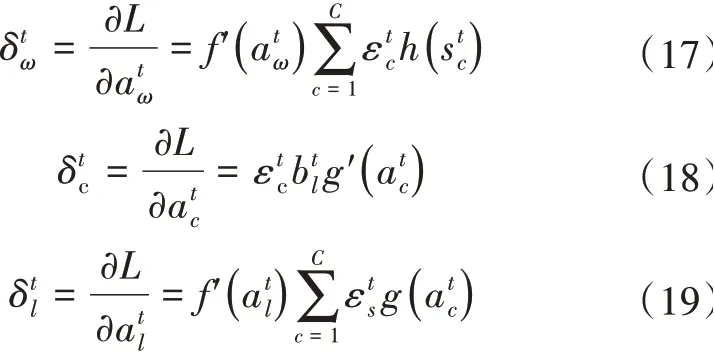
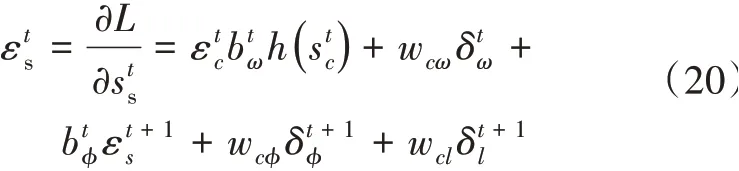
根据残差的计算公式，可以得到长短时记忆神经网络节点i与j之间的权值更新公式为

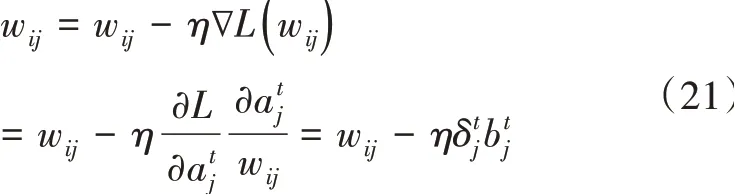
不断更新得到新权值，直到长短时记忆神经网络的输出误差达到预先设定的范围，则长短时记忆神经网络就终止学习，得到最优的长短时记忆神经网络结构。

1.3 深度学习算法的城市轨道交通短时客流量预测

Step1：收集城市轨道交通短时客流量数据，将它们按时间先后顺序组成一个一维的时间序列数据。

Step2：采用互信息法计算城市轨道交通短时客流量的时间延迟，并采用Cao法确定城市轨道交通短时客流量的最优嵌入维数。

Step3：采用时间延迟和最优嵌入维数对城市轨道交通短时客流量时间序列进行重构，建立城市轨道交通短时客流量预测的训练样本集和测试样本集。

Step4：长短时记忆神经网络对城市轨道交通短时客流量预测的训练样本集进行学习，计算网络输出和城市轨道交通短时客流量期望值之间的误差，根据误差不断更新权值，当达到给定的训练次数或者误差时，结束长短时记忆神经网络训练。

Step5：根据训练好的长短时记忆神经网络建立城市轨道交通短时客流量预测模型。

Step6：采用测试样本集对城市轨道交通短时客流量预测模型的性能进行测试，并对测试结果进行分析。

2 城市轨道交通短时客流量预测效果验证性测试

2.1 测试对象

为了测试本文设计的深度学习算法的城市轨道交通短时客流量预测模型的性能，选择一段时间的交通客流量作为测试对象，它们的变化曲线如图2所示。

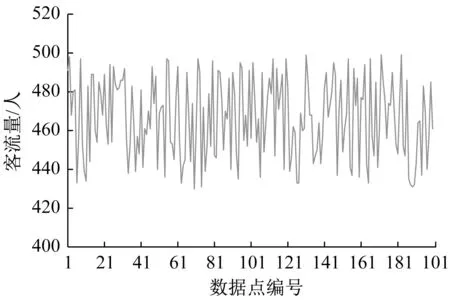
图2 城市轨道交通短时客流量的历史数据Fig.2 Historical data of short-term passenger flow of Urban Rail Transit

2.2 城市轨道交通短时客流量数据的混沌分析和处理

对图2的城市轨道交通短时客流量数据进行分析可知，其具有较强的随机性变化特点，采用互信息法和Cao法确定城市轨道交通短时客流量的时间延迟和最优嵌入维数，具体如图3和图4所示。进一步分析发现，城市轨道交通短时客流量数据的时间延迟和最优嵌入维数最优值分别为6和7，采用此值对图2的城市轨道交通短时客流量数据进行重构，选择最后50个数据作为测试样本，其他为训练样本。

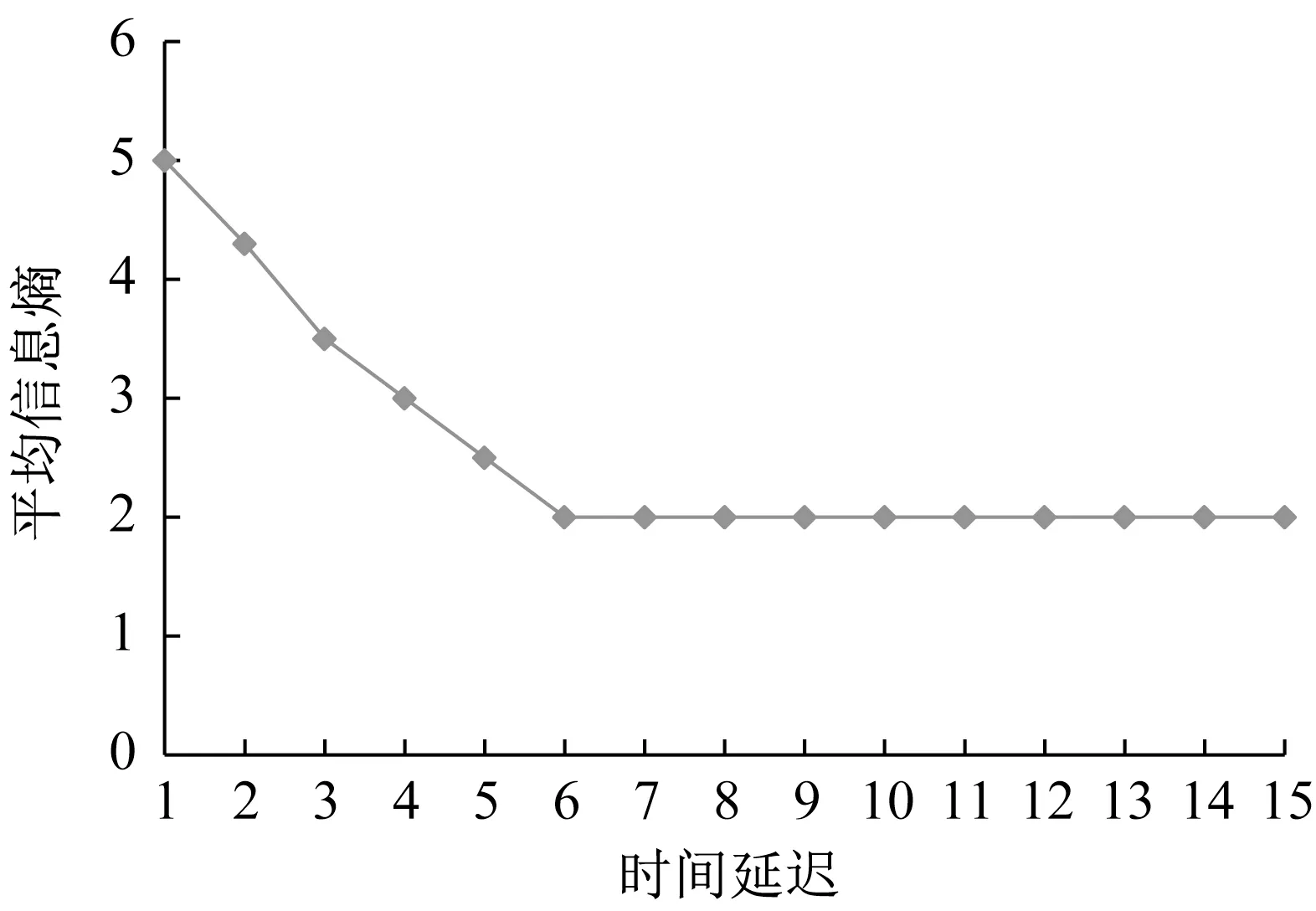
图3 城市轨道交通短时客流量数据的时间延迟Fig.3 Time delay of short-term passenger flow data of Urban Rail Transit

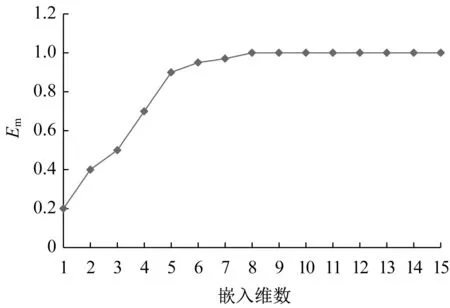
图4 城市轨道交通短时客流量数据的嵌入维数Fig.4 Embedding dimension of short-term passenger flow data of Urban Rail Transit

2.3 本文模型的城市轨道交通短时客流量预测效果

采用本文模型对50个城市轨道交通短时客流量测试样本进行预测，结果如图5所示。对图5的城市轨道交通短时客流量实际值和预测值进行分析，可以发现本文模型可以高精度跟踪城市轨道交通短时客流量变化趋势，城市轨道交通短时客流量预测误差极小，可以满足实际的城市轨道交通管理要求。

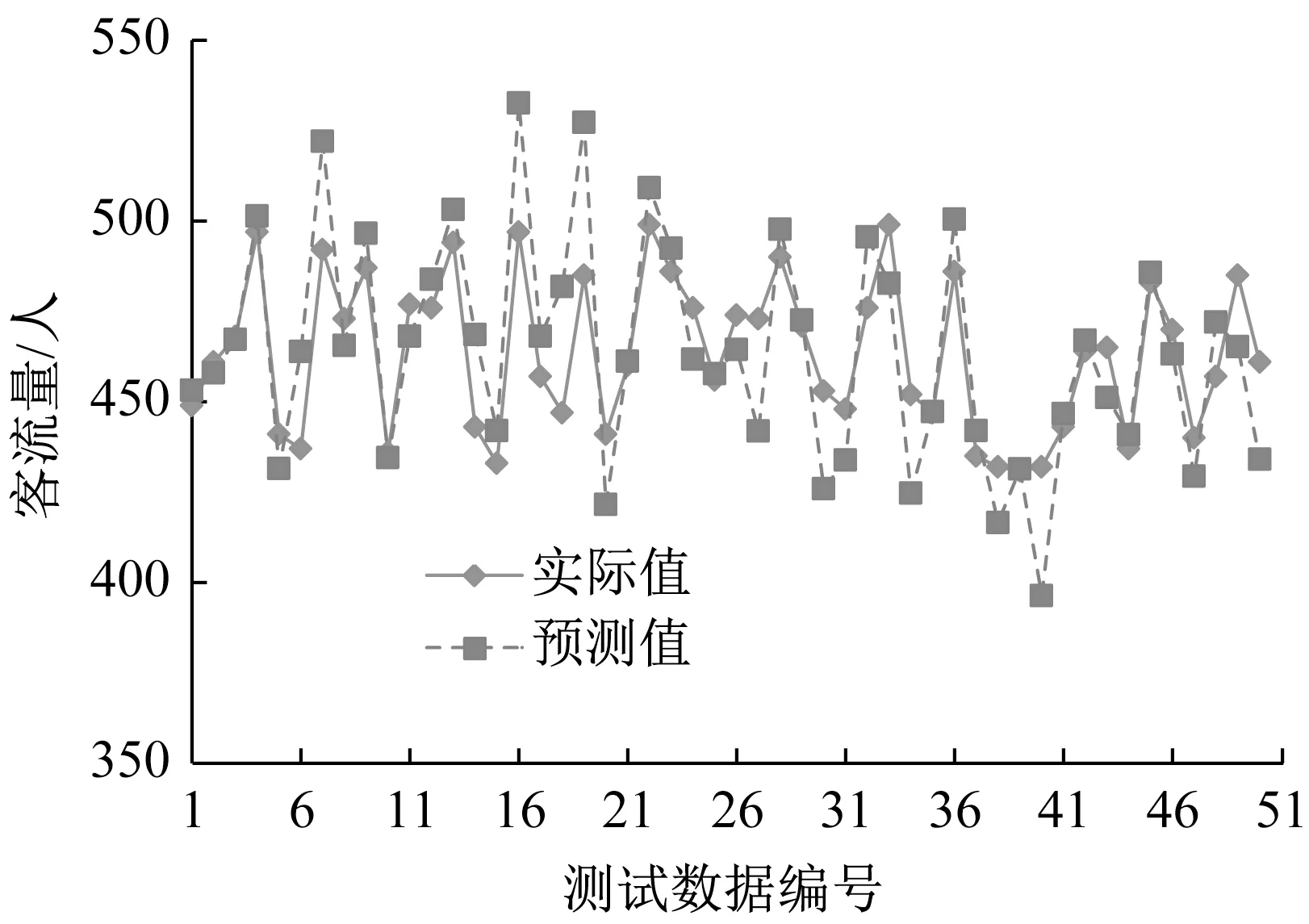
图5 本文模型的城市轨道交通短时客流量预测结果Fig.5 Prediction results of short-term passenger flow of urban rail transit based on the model in this paper

2.4 与其他模型的城市轨道交通短时客流量预测结果对比

为了测试本文模型对于城市轨道交通短时客流量预测效果结果的优越性，选择没有进行混沌分析的长短时记忆神经网络（LSTM）、混沌分析+BP神经网络（Cao-BPNN）的城市轨道交通短时客流量预测模型进行对比测试，采用平均绝对误差（MAE）和平均绝对百分比误差（MPAE）作为预测结果准确性评价标准，计算公式分别为

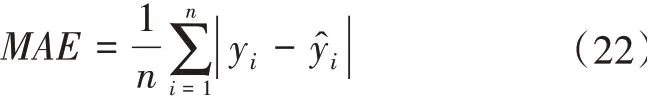
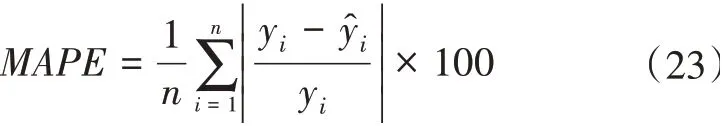
式（23）中，yi和y^i分别为城市轨道交通短时客流量第i个真实值和预测值；n表示样本总量。

不同模型的城市轨道交通短时客流量结果指标如表1所示。对表1进行分析可知，相对于LSTM，本文模型的平均绝对误差减少了4.32%，相对于Cao-BPNN，本文模型的平均绝对误差减少了4.34%，这表明本文模型能够获得理想的城市轨道交通短时客流量预测结果，可以有效提高城市轨道交通短时客流量预测精度，验证了本文模型在城市轨道交通短时客流量预测中的优越性。

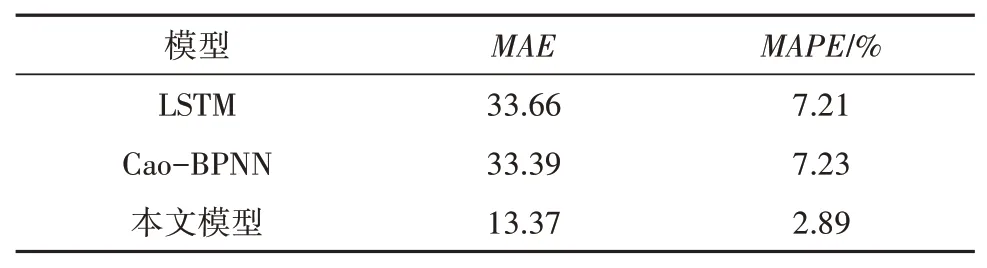
表1 城市轨道交通短时客流量预测结果的多指标对比Tab.1 Multi index comparison of short-term passenger flow prediction results of Urban Rail Transit

3 结 语

城市轨道交通短时客流量变化具有一定的规律性，同时具有一定的随机性，为了降低城市轨道交通短时客流量预测偏差，结合城市轨道交通短时客流量变化特点，采用深度学习算法对其进行建模与预测，与经典模型测试结果对比，深度学习算法能够高精度拟合城市轨道交通短时客流量变化趋势，城市轨道交通短时客流量预测整体效果明显优于经典模型，解决了当前城市轨道交通短时客流量预测过程中存在的一些问题，可以对城市轨道交通运力的合理配置提供一定的参考借鉴，具有较高的实际应用价值。