基于稀疏约束的DCD滑动窗RLS水声信道估计算法研究

梁仕杰，王 彪，张 岑

(江苏科技大学电子信息学院，江苏镇江212003)

0 引 言

水声信道的多径效应强、可利用带宽窄，信号衰减严重等特点使得水声通信的发展受到限制。利用水声信道的稀疏性，研究稀疏信道估计算法可以极大地改善水声通信的性能。

目前，稀疏信道估计问题一般通过压缩感知算法[1-2]或自适应滤波算法来解决。基于压缩感知的信道估计方法如正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)，正则化正交匹配追踪算法(Regularized Orthogonal Matching Pursuit, ROMP)等虽然可以根据少量的信息通过信号的重构[3]来估计信道，但这些方法需要信道稀疏度的先验信息[4]，这限制了此类方法的应用。

自适应滤波算法主要有最小均方(Least Mean Square, LMS)算法、最小二乘(Least Square, LS)算法及递归最小二乘(Recursive Least Squares, RLS)算法等。LMS算法是基于均方误差的算法，利用 LMS算法所估计的滤波器系数与数据的统计特性有关，因此其收敛速度较慢。而利用LS算法[5-6]估计信道，收敛速度较快。RLS算法在LS算法的基础上引入了遗忘因子[7]，虽然在一定程度上改善了LS算法的性能，但是其未对信道系数进行范数约束，因此在稀疏信道估计问题上效果并不好。文献[8-9]将范数约束的概念引入到稀疏信道估计中，估计性能较传统算法有明显提高。本文在时域以高斯训练序列为处理对象，在现有理论的基础上，将惩罚函数加入到RLS算法的代价函数中，对估计信道系数进行范数约束，同时利用滑动窗方式处理代价函数，在改善稀疏信道估计性能的同时又降低了 RLS算法的复杂度。此外，将二分坐标下降(Dichotomous Coordinate Descent, DCD)[10]算法应用于单次迭代代价函数最优解的搜索中，进一步降低了算法的复杂度，对稀疏信道估计的研究具有一定的意义。

1 基于范数约束的DCD滑动窗RLS信道估计原理

1.1 信道估计问题的实质

通信系统的接收信号在时域中表示为

1.2 RLS自适应滤波算法的原理

自适应滤波主要利用前一时刻获得的滤波器参数，根据估计误差自动调节当前时刻的参数，使得某个代价函数达到最小，从而实现最优滤波。

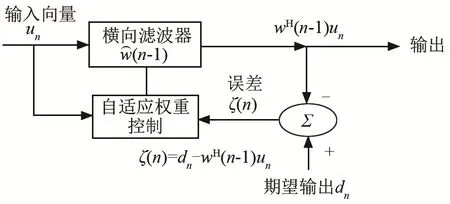
图1 自适应滤波算法原理图Fig.1 Schematic diagram of adaptive filtering algorithm

RLS自适应误差算法的代价函数为

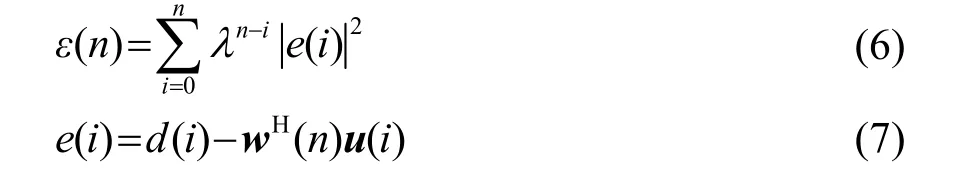
与LS算法相比，RLS算法引入遗忘因子，其作用是离当前时刻近的误差赋较大权重，离当前时刻远的误差赋较小权重，从而减小过去较远时间点的误差影响，使滤波器平稳工作。

1.3 基于范数约束的DCD滑动窗RLS算法原理

2 本文算法的信道估计步骤

3 仿真与分析

仿真所选信道为稀疏时不变信道，其时域信道冲激响应模型为

其中，L是具有不同时延的多径数目，h(l)是第l条路径下的信道增益，τl是第l条路径下的时延差。

3.1 惩罚函数对估计结果影响

仿真采用的高斯训练序列的长度为 7 000，信道采样点数为 2 000，采样频率为 128 kHz。迭代5 000次，信噪比为25 dB。图2是本文采用的DCD滑动窗-Lasso RLS算法估计结果、RLS算法估计结果以及实际信道系数的对比图。由图2可知，RLS算法与本文采用算法在信道的抽头系数处估计精度相似，但是RLS算法估计结果在信道零系数位置处普遍存在波动，因而其对稀疏信道估计的结果较差。本文采用的算法利用Lasso惩罚函数对信道系数进行了l1范数约束，使稀疏信道估计精度更高。

图2 惩罚函数对估计结果的影响Fig.2 The effect of the penalty function on the estimated result

3.2 不同种类惩罚函数的估计性能对比

本节主要通过每次迭代所估计的信道系数与实际信道系数的归一化均方误差(Normalized Mean Square Error, NMSE)来反映各算法信道估计的性能。其数学表达式为

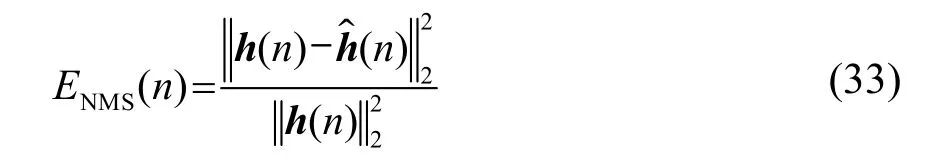
本部分对比了代价函数采用三种不同惩罚函数时的估计性能。高斯训练序列长度为 7 000，信道采样点数为2 000，迭代次数为5 000，信噪比为25 dB，结果如图3所示。由图3可见，经过5 000次迭代，DCD滑动窗-Lasso RLS(套索惩罚函数)算法的估计性能最好，这是因为它代价函数中的Lasso 惩罚函数用l1范数来约束信道系数，将绝对值较小或影响因子较小的自变量的回归系数置为 0，这使得它更适用于稀疏信道估计，DCD滑动窗-ElasticNet RLS(弹性网惩罚函数)算法的β值为0.6，其性能介于 DCD滑动窗-Lasso RLS算法和DCD滑动窗-Ridge RLS(岭回归惩罚函数)算法之间。

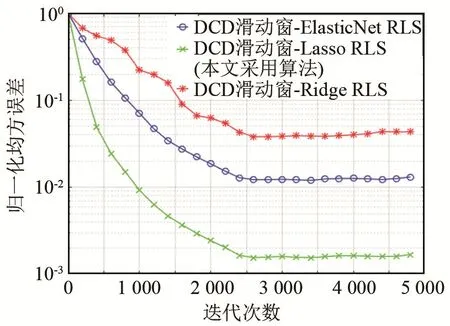
图3 不同惩罚函数的估计性能对比Fig.3 Comparison of estimation performance between different penalty functions

3.3 不同信道估计算法的估计性能对比

本节分析了本文采用算法与传统信道估计算法的性能。信噪比在 5～30 dB变换，变换间隔为5 dB。不同信道估计算法的归一化均方误差如图4所示。在LS信道估计过程中，256个子载波每隔8个子载波插入导频。OMP算法采用随机导频。RLS算法和DCD滑动窗-Lasso RLS算法均通过时域插入长度为1000的高斯训练序列。由于OMP算法感知矩阵中的傅里叶变换矩阵列数与信道长度相同，若信道长度过大，将会大大增加仿真的复杂度，因此稀疏信道采样点数取为100。由图4可知，所有算法的归一化均方误差都随信噪比的增加而下降，LS算法虽然简单易实现，但其估计精度远低于其余三种算法。这是由于LS算法在估计稀疏信道时忽略了噪声的影响，所以信道估计值对噪声干扰的影响比较敏感。同时，由于LS方法的整体估计精度不高，因此其信道估计性能比较其他算法变化波动较小。RLS算法估计精度略优于OMP算法，本文算法在四种信道估计算法中性能最优。

图4 不同信道估计算法的归一化均方误差Fig.4 Normalized mean square error of different channel estimation algorithms

3.4 不同信道估计算法的复杂度对比

通过CPU运行时间分析不同信道估计算法的复杂度，结果如图5所示，仿真信噪比为15 dB。基于压缩感知的信道估计方法的迭代次数和稀疏度K值有关，因此OMP算法受K值的影响较大，K值越大，其复杂度越高。本文采用的DCD滑动窗-Lasso RLS算法与RLS算法相比，用滑动窗方法处理代价函数并且应用 DCD算法搜索其最优解，减少了算法的复杂度。与LS算法相比，本文算法因在代价函数中添加了范数约束项，所以其复杂度略高于LS算法，但其信道估计精度远高于LS算法。

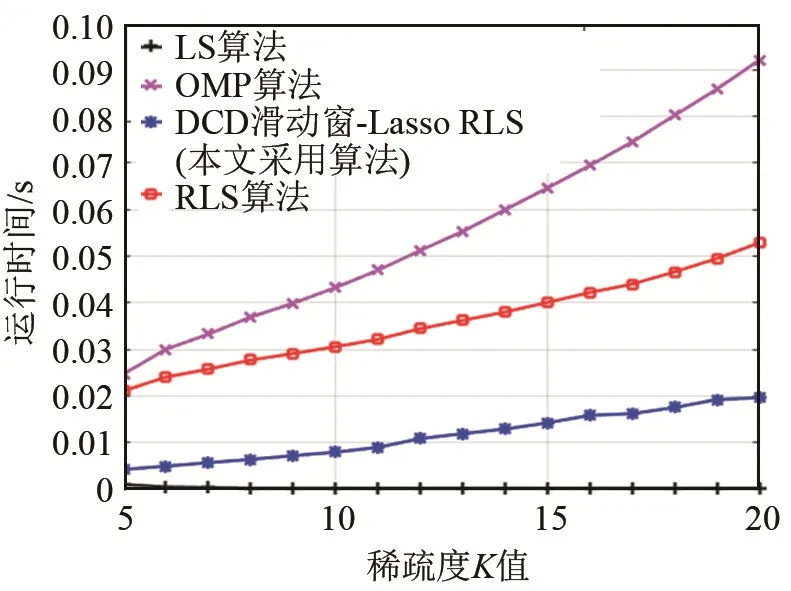
图5 不同信道估计算法的CPU运行时间Fig.5 CPU running time of different channel estimation algorithms

4 结 论

本文提出了一种基于时域训练序列的自适应稀疏信道估计算法。为解决传统算法在稀疏信道估计方面精度低的问题，在经典RLS算法的代价函数中添加了惩罚函数项，用以对信道系数进行范数约束。仿真结果表明本算法相较于传统信道估计算法，提高了稀疏信道估计的精度。此外，所提算法在其代价函数中应用滑动窗处理方法并通过 DCD算法搜索代价函数的最优解，仿真结果表明本算法相较于其他信道估计算法具有较低的复杂度。因此将本算法应用于稀疏信道估计中具有一定的意义。