基于小波神经网络耦合模型对云南星云湖富营养化气象驱动因子的分析*

潘佳敏，冯禹昊，谢 平，方精云**

(1:北京大学城市与环境学院，北京 100871)(2:云南大学生态与环境学院高原湖泊生态与治理研究院，昆明 650091)

水体富营养化是全球性的问题[1-2]，1980s以来，全球68%的湖泊有富营养化恶化的趋势[3]，并且一些地区的湖泊出现有害蓝藻水华[4]，给生态环境、人类健康造成极大的负面影响[5]，且引起大量的经济损失并带来高昂的治理费用[6]. 我国云南湖泊富营养化严重，星云湖作为云南湖泊中水质恶化最为迅速的小型湖泊，易受到外界因素的干扰，现已重度富营养化，并常年暴发蓝藻水华[7]. 为治理星云湖的水体污染，政府在“十二五“期间及“十三五”期间投入资金分别高达6亿元和27亿元以上[8-9]. 过去对星云湖水质的研究主要集中在面源污染如地表覆盖变化的影响[10-13]，也有研究探究了内源污染沉积物[14]、营养盐浓度[15]和人类活动[16]对星云湖水质的影响. 而探究气候因子对星云湖水质影响的研究较少，且仅停留在描述性分析方面[17]. 气象因子是影响小型湖泊富营养化程度的重要因素，利用现存气象数据探究该湖泊类型富营养化的驱动因素是具有现实意义的.

湖泊富营养化是外界环境因子的综合影响下的复杂结果. 由人类活动导致的湖泊中氮、磷等污染物超标是水体富营养化程度加剧的主要驱动因素[18-19]，但在营养盐条件充足的条件下，气象因子是环境因子中影响湖泊富营养化程度的主要限制因子. 湖泊富营养化程度和气象因子均具有周期型波动的特点，且不同气象因子影响湖泊的富营养程度的机制不同：降雨量的增加会促进磷的迁移加剧富营养化[20-21]；气候变暖会改变湖泊中氮、磷浓度，进而改变湖泊中植物群落的组成[22]；水温、风速、太阳辐射是影响湖泊浮游植物丰度和分布的重要因素[23]等. 诸多学者探究了气象因子对湖泊富营养化程度的影响大小：罗晓春等采用随机森林算法计算了导致太湖富营养化发生的各主导气象因子的贡献率[24]；Li等将气象因子与其他环境因子作为解释变量建立多元回归模型，探讨了中国巢湖浮游生物量年内、年际变化[25]；类似的研究还在湖北长湖[26]、滇池[27]、千岛湖[28]等湖泊开展. 这些研究就湖泊富营养化的发生机制和影响因素进行了全面的探索，并提供了相应的研究范式，但仍存在以下两点待改善之处：其一，对湖泊特定气候条件下导致的富营养化程度的讨论不充分. 以上研究更多侧重的是年际变化的趋势，较少根据月度数据进行讨论. 且针对降水量、温度、风速和日照时间4类主要气象因子进行讨论的研究较少. 其二，多采用传统的线性统计分析方法，但变量之间多存在非线性关系，难以描述多因素特别是气象因子对富营养化这个复杂过程的影响，因此寻找新的方法对该过程进行度量是非常必要的.

BP神经网络(又称多层前馈神经网络或反向传播网络)是目前应用最为广泛的一类人工神经网络，已用于水体的水质评价[29]、海岸的藻类水华模拟[30]、湖泊叶绿素a预测[31]等方面. 小波变换是多分辨率分析方法并且具有良好的局部检测功能，适合表征数据变换的瞬态和奇异点特征，且可以保持频率特性品质因数恒定，常用于噪声祛除、多尺度趋势分析[32]. 将小波分析和神经网络两种方法进行耦合，可以结合两者优势构建更好的分析模型：一方面是能优化模型的输入数据，即通过小波分析后的数据训练神经网络模型，可剔除或降低遥感数据和气象站点数据本身存在的误差、噪声或异常值的干扰，保留所需尺度下的数据信息，进而降低过拟合风险，增强模型的可信度和泛化能力；另一方面能构建的多个模型进行评判筛选，即将小波分析提供的大量不同时间尺度的数据作为输入数据，构建多个模型，并从中选出合适的时间尺度下的最优模型，能有效提升模型性能.

本文将云南星云湖的水华强度指数作为输出数据，将月降水量、月平均温度、月平均风速、月日照时数4个主要气象因子作为输入数据，构建并筛选最优小波-神经网络耦合模型，并将其与BP神经网络对比分析. 探讨了气象因子对星云湖富营养化程度和变化周期的影响，为星云湖的保护与富营养化的治理提供参考依据.

1 资料与方法

1.1 数据来源

1.1.1 气象因子数据来源 气象数据来自国家气象科学数据中心(http://data.cma.cn/)，选取1986-2011年玉溪基本站(区站号：56875)20-20时月降水量、月平均气温、月平均风速和月日照时数4个气象因子作为研究变量. 图1为4个气象因子年内变化情况箱式图，“×”表示月均值，可看出星云湖流域各月度气象因子的变化特征，其具有热带季风性、高原山地气候的特点.

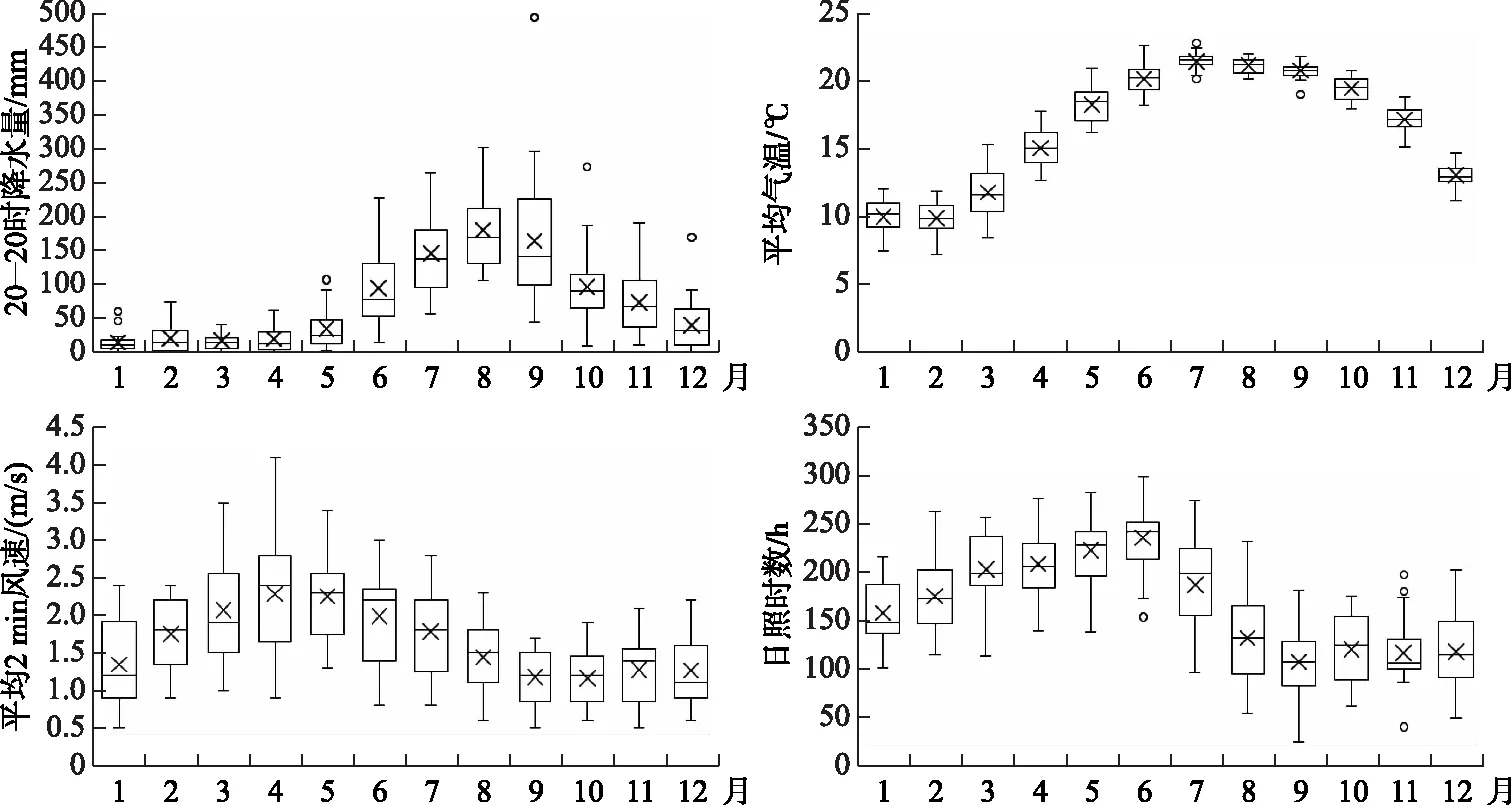
图1 1986-2011年气象因子年内变化情况

1.1.2 水华强度计算方法及其处理 本文选取的是美国陆地卫星系列第五颗卫星(Landsat 5)TM成像传感器的大气表观反射率(TOA)产品，Landsat 5的重返周期为16 d，其中6个无量纲大气表观反射波段的空间分辨率均为30 m. 整个运算过程在Google Earth Engine(GEE,https://developers.google.com/earth-engine/)平台进行，根据星云湖所处位置，我们对1986-2011年间每个月的遥感数据进行搜索、运算、取月平均值、裁剪，最终获得共计211个月的数据. 具体的计算过程如下，在根据Landsat 5 TM TOA中BQA波段数据提供的信息进行除云之后，利用Ho等提出的水华监测算法计算逐月的平均近地面水华强度[3]：

B=FG(Band4-1.03·Band5)

(1)

式中,B为水华强度，每个像素点的取值范围介于0～0.1之间；Band4是L5 TM的第4波段大气表观反射率(无量纲)；Band5是L5 TM的第5波段大气表观反射率(无量纲). 而FG为绿度滤波器，筛选出色调低于阈值H的像元，其计算公式如下：

(2)

判断条件中的阈值H的计算方式如下所示：

(3)

式中, Band1是L5 TM的第1波段大气表观反射率(无量纲)；Band2是L5 TM的第2波段大气表观反射率(无量纲)；Band3是L5 TM的第3波段大气表观反射率(无量纲).

根据上述算法，得到星云湖211幅月均水华强度B的遥感图像，其每幅图像的栅格数据情况如图2所示，横坐标表示图像中存在的有效数据的栅格数量与掩膜栅格总数的比值(有效栅格占比)，纵坐标表示图像数量，选取有效栅格占比0.8作为图像的筛选阈值，大于0.8的遥感图像是符合条件的，最终有193个月的有效图像数据. 再分别对每幅月均水华强度B的图像中所有栅格的数值取平均值，作为当月星云湖的平均水华强度B，各月份数据存在情况如表1所示.

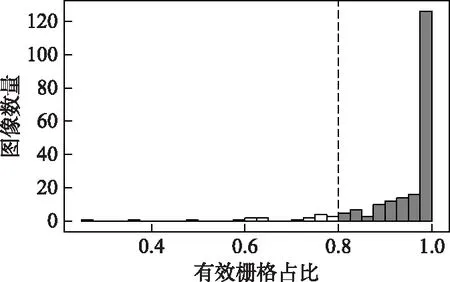
图2 水华强度B图像的有效栅格占比频数分布直方图

表1 各月份的水华强度B

1.2 小波-神经网络耦合模型基本原理

1.2.1 小波分析 小波分析把时间和频率作为独立变量, 将一维原始信号在时间和频率两个方向上展开, 从而清楚地了解时间序列的不同时域尺度上的频率特征, 实现对时间序列数据的多时间尺度分解. 具体地，连续小波变换可以定义为[33]：

(4)

式中,x(t)为原始信号；ψ(t)为小波母函数；a为尺度因子；τ为位移因子；*表示共轭；积分结果W(a,τ)为小波系数，反映了尺度为a、位移为τ时的小波函数与原始信号间相关性的强弱.

Morlet小波是一种单频复正弦调制的高斯波，具有很好的时域和频域局部性，常用于信号的分解和时频分析中，且能消除用实小波变换系数作为判据产生的虚假振荡，其小波母函数的时域形式如下[33-34]:

(5)

式中,fb为小波带宽，fc为小波中心频率，i为虚数符号.

1.2.2 神经网络基本原理 80%～90%的人工神经网络模型采用的是BP神经网络或它的变形. BP神经网络由一个输入层，一个或多个隐藏层和一个输出层构成，每一层由一定数量的神经元构成[35]. BP算法是一种监督式的学习算法，由两部分组成：信息的正向传播与误差的反向传播. 在正向传播过程中，输入信息从输入端经隐藏层逐层计算传向输出层，每一层神经元的状态只影响下一层神经元的状态. 如果在输出层没有得到期望的输出，则计算输出层的误差变化值，然后转向反向传播. 通过网络将误差信号沿原来的连接通路反传回来修改各层神经元的权值直至达到期望目标. 其主要思想是：对于q个输入学习样本：P1，P2，…，Pq，已知其对应的输出样本为： T1，T2，…，Tq. 学习的目的是用网络的实际输出A1，A2，…，Aq与目标矢量T1，T2，…，Tq之间的误差来修改其权值，使Am(m=1，2，…，q)与期望的Tm，尽可能接近. 即：使网络的输出层的误差平方和达到最小. 它是通过连续不断地在相对于误差函数斜率下降方向上计算网络权值和偏差的变化而逐渐逼近目标的. 每一次权值和偏差的变化都与误差的大小呈正比，并以反向传播的方式传递到每一层[36].

1.2.3 小波-神经网络耦合模型构建 整个模型的耦合包括：(1)对气象因子的小波分析；(2)基于小波分析输出数据，构建并筛选多个BP神经网络. 图3为两种模型的耦合过程图，具体如下：首先利用Matlab R2018b软件自带的小波工具包对各气象因子原始信号进行Morlet小波分析分解，将接近于且略大于有效数据193的数值作为最大时间尺度，其设定为200月. 以1个月为单位，输出得到200个不同时间尺度下各气象因子的小波系数. 对每个时间尺度下，删除仅存在气象因子小波系数但不存在水华强度B的月份数据，再对剩下的气象因子小波系数进行数据标准化，将标准化后的193*4的气象因子矩阵的小波系数作为BP神经网络的输入数据和对应月份的水华强度B作为BP神经网络的输出数据，其中设定BP神经网络随机选取70%的数据作为训练集，15%的数据作为测试集，15%的数据作为验证集. 本文将BP神经网络的隐藏层个数设置为1层，而对于隐藏层神经元个数N的确定，目前尚无理论依据和有效方法，本文的解决方法为对BP神经网络分别设定2～12个隐藏层神经元个数进行测试，由此得到200个不同时间尺度下，具有2～12个隐藏层神经元个数的BP神经网络. 最后根据各小波-BP神经网络耦合模型的拟合优度(R2)最大的原则筛选出最优小波-BP神经网络耦合模型. 其中，R2的计算公式如下：

(6)

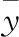
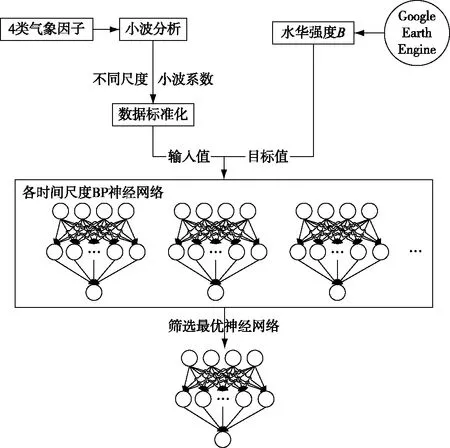
图3 小波-神经网络耦合模型构建过程

2 结果与分析

2.1 最优小波神经网络模型的筛选结果

图4为在200个不同时间尺度下，具有2～12个不同隐藏层神经元个数N的小波-BP神经网络耦合模型的拟合优度(R2)峰峦图. 通过计算模型的R2来评价模型对原始数据拟合程度，R2值越接近1，说明模型对观测值的拟合程度越好；反之，R2值越小，说明模型对观测值的拟合程度越差. 根据图4所展示的计算结果，R2大多分布在0～0.4之间. 当隐藏层神经元个数N为9，时间尺度为11月的情况下，神经网络的R2达到最高，为0.605，此时耦合模型效用最高. 同时也说明通过选取合适的隐藏层神经元个数，可以有效提升小波-神经网络耦合模型性能.

图4 不同隐藏层神经元个数(N)下200个不同尺度小波-神经网络耦合模型的拟合优度(R2)

表2为设定在不同隐藏层神经元个数(N=2, 3, …, 12)的情况下，小波-神经网络耦合模型的最优时间尺度和与其对应的性能参数情况. 隐藏层神经元个数不同时，最优模型对应的时间尺度不同，但大多接近于12或者接近于12的倍数. 这与输入数据气象因子的波动周期一致，说明最优模型对应的时间尺度受气象因子的波动周期影响，也证实了气象因子的波动周期也是影响水华强度B变化的重要因素. 模型性能参数包括均方误差(MSE)及回归系数(R)，回归系数中的ValidationR反映的是模型的泛化性能，TotalR反映的是模型对所有数据的拟合情况，当MSE越小，R越接近1时，模型的效用越高. 由表2可知，当N为7时，MSE最小；当N为10时，ValidationR最大；当N为9时，TotalR最大. 综合考虑，本文选择隐藏层神经元个数为9的小波-神经网络模型作为最优神经网络.

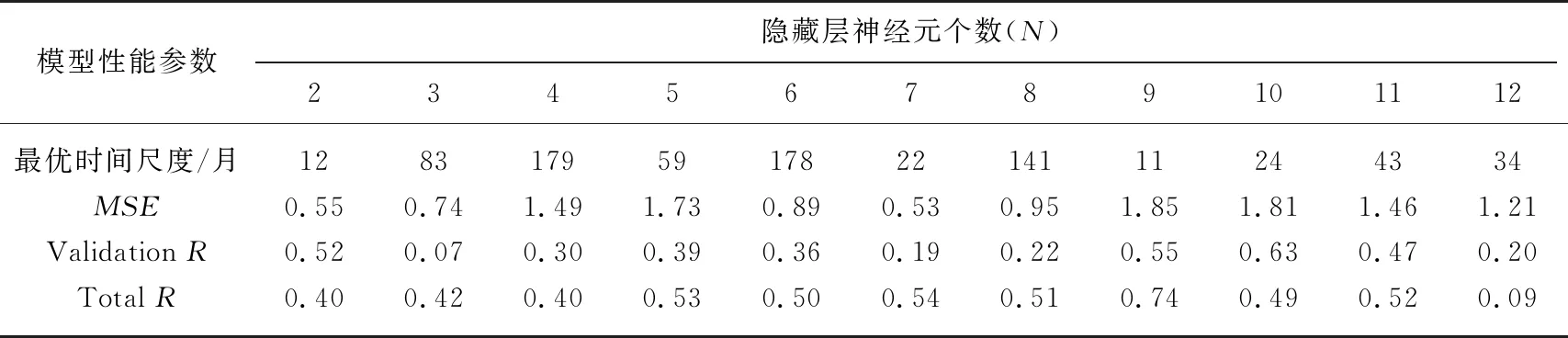
表2 不同隐藏层神经元个数(N)下小波-神经网络耦合模型的最优时间尺度及该尺度下的模型性能参数

2.2 不同模型的拟合效果及气象因子的平均影响值比较

为了与以上最优小波-神经网络耦合模型进行比较研究耦合效果，本研究另构建了隐藏层为1，具有不同隐藏层神经元个数(N=2, 3, …, 12)的BP神经网络，并用标准化后的气象原始数据和水华强度B分别作为输入输出数据训练网络，拟合参数结果如表3所示. 并以R2最大的原则，最终确定利用隐藏层神经元数N为9的BP神经网络与最优小波-神经网络耦合模型进行比较.

表3 不同隐藏层神经元个数下的BP神经网络

图5 两类模型数据拟合情况对比

图5展示的是两种模型数据拟合的具体情况，空心点表示水华强度B标准化后的值，实线为模型输出值和目标值的拟合直线，虚线为1∶1线. 结果显示在训练集、测试集、验证集和总体数据中，最优小波-神经网络耦合模型的R均高于BP神经网络模型中的R，也就是说在加入小波分析进行模型耦合并筛选后，模型对数据拟合效果有明显的提升. 但当水华强度B处于较高水平时，所有的拟合线均低于1∶1线，说明在水华强度较高的情况下，两类模型的拟合效果表现较差，这与缺少高水平水华强度B的数据有关(表1).

图6 两种模型各气象因子平均影响值MIV大小

BP神经网络的平均影响值法(简称MIV算法)被认为是在神经网络中进行敏感变量筛选和评价变量重要性的最好方法之一. 在本文中评价各气象因子影响大小的具体过程是：将训练数据的每个气象因子增加10%或者减小10%得到的两组新训练数据的自变量，代入用原始训练数据训练好的BP神经网络，分别得到两组数据的估计结果，而这两组估计结果的差值被称为IV，对结果取平均为平均影响值(MIV)，依次算出各个自变量的MIV，就能确定各个输入变量对网络结果的影响程度[37]. 图6显示了各气象因子在BP神经网络模型和最优小波-神经网络耦合模型中MIV的大小，各气象因子的MIV反映对模型结果的影响程度，正负值分别代表促进作用和抑制作用. 对于BP神经网络模型来说，影响估计值大小的主要因子是月降水量，其次是月平均风速和月平均气温抑制作用，而月日照时数促进作用较小，这与过去该4个气象因子对湖泊富营养化程度起到促进作用的研究结果相差甚远[20-24]；而对于最优小波-神经网络耦合模型来说，4个气象因子均为促进作用，月平均气温对估计值的影响最大，其次是月降水量和月平均风速，月日照时数影响最小. 对比两种模型各气象因子的MIV大小可知，最优小波-神经网络耦合模型相比BP神经网络对气候因子的变化更为敏感. 且根据以往的研究结果，在最优小波-神经网络耦合模型中，各气象因子对湖泊富营养化的发生机制的解释更合理.

3 讨论

1980s以来，云南星云湖流域工农业发展迅速，工业废水、生活污水的排放导致星云湖的生态环境逐步恶化、富营养程度加深[38]，甚至暴发有害蓝藻水华[15]. 很多研究讨论了面源污染、内源污染、人类活动和营养盐对星云湖富营养化程度的影响[10-16]，但尚不多见探究气象因子对星云湖富营养化程度影响的相关研究. 而诸多文献表明气象因子是影响湖泊富营养化程度的关键因素[20-23]. 罗晓春等的分析结果表明气温是影响太湖蓝藻水华综合指数的主导因子，其次是风速、降水，最后是日照时间[24]，这与本文的研究结果基本一致. Brias等研究表明年内降水的变化是导致湖泊富营养化程度加剧的主要驱动因素[21]，而本文进一步补充发现气象因子的波动周期也是影响年内水华强度变化的重要因素.

本文根据气象站点月度气象因子及遥感图像数据所算出的水华指数，构建并筛选合适的模型用于描述星云湖富营养化程度变化并探讨各气象因子对富营养化程度的影响大小是极具意义的. 郭志海等发现星云湖水质状况与植被指数NDVI具有关联性[39]，这进一步证实了遥感数据在星云湖应用的有效性. 由于遥感数据和气象站点的数据不可避免出现误差和异常值，直接利用这些数据进行拟合分析会使构建的机器学习模型产生精度方面的问题. 于家斌等分析表明对叶绿素a浓度数据平滑后再利用神经网络能更好地预测蓝藻水华的暴发[40]，这与本文所采取方法的本质相似. 小波分析方法本身能对周期性变化的数据进行分析，本文发现其能降低数据异常和数据误差带来的影响，将小波分析与BP神经网络耦合，能有效提升BP神经网络对数据拟合效果和模型的泛化效果. 本文最终将隐藏层神经元数为9、时间尺度为11月的小波-神经网络耦合模型作为最优模型，并将此与无耦合BP神经网络进行比较，发现前者对于星云湖富营养化程度的拟合更加精确，也验证了在小型湖泊用气象数据变化拟合富营养化程度变化的可行性. 本文显示了小波-神经网络耦合模型的优越性，该研究方法可以延申至有关于富营养化其他类似小型湖泊的研究.

本文仍然存在一定局限性，首先，样本量数据不大，尤其是高水华强度值的样本量较少，导致模型对高水华强度值的拟合效果低，进而影响小波-神经网络耦合模型整体的拟合优度. 其次，气象因子只能解释部分星云湖富营养化程度变化的波动情况，并没有将营养盐浓度、面源污染、内源污染等人为因素和其他因子纳入模型，难以精确拟合实际的湖泊富营养化程度. 这些不足可在今后的研究中进行补充或探讨.

4 结论

1)在对最优小波-神经网络模型进行筛选的过程中，不同隐藏层神经元下的最优小波时间尺度与气象因子的波动周期或波动周期的倍数一致或者接近，证实了气象因子的波动周期是影响年内水华强度变化的重要因素.

2)将最优小波-神经网络耦合模型与无耦合BP神经网络模型进行比较发现，小波-神经网络耦合模型能有效提高数据拟合的精度. 最优小波-神经网络耦合模型的拟合优度为0.605，高于BP神经网络的拟合优度0.292. 且小波-神经网络耦合模型的均方误差MSE和相关系数R均优于BP神经网络，能更有效地对星云湖富营养化程度进行分析和描述.

3)分别用最优小波-神经网络耦合模型和无耦合BP神经网络模型计算各气象因子的平均影响值，发现最优小波-神经网络耦合模型的结果更加符合湖泊富营养化发生的机制. 根据最优小波-神经网络耦合模型的各气象因子的平均影响值，得到月平均气温是影响星云湖富营养化的主导气象因子，其次是月降水率、月平均风速，最后是月日照时数.