厚板轧制过程中轧件内部变形渗透定量化研究——自主工艺设计辅助软件的探索

王全胜,袁向前

(宝山钢铁股份有限公司中央研究院,上海 201999)

1 概述

厚板轧制所用的坯料,如钢锭或连铸坯,内部存在较多的缺陷,尤其在厚度1/2和1/4处,比其他位置存在更多的缺陷。通过厚板加热炉对坯料进行均匀加热,再通过厚板轧机对坯料进行轧制,尽量让轧件内部获得较多的变形量,以改善或消除轧件内部的缺陷,并在后工序辅以合适的冷却工艺或者热处理,最终获得性能良好、均匀的厚板。因此,厚板轧制过程中,轧件内部获得变形量的多少,尤其在轧件厚度1/2和1/4处的变形量,对于轧后钢板内部的组织性能均匀性,特别对于高钢级的厚板产品,起着至关重要的作用[2-3]。

当前,在厚板产品轧制工艺设计时,一般会提及到压缩比,即板坯厚度与钢板目标厚度的比值。通过分析压缩比这一参数的合理性,来判断板坯在轧制过程中其内部获得变形量的多少,进一步辅助判断轧后钢板的性能是否能达到设计要求。然而,厚板在轧制过程中,受限于坯料尺寸和轧机能力,往往在轧件表面或者近表面范围内获得较多的变形量,而在轧件心部获得较少的变形量。生产过程中,这种变形量分布不均匀的现象,通常表现为在轧件或者钢板在边部出现严重的双鼓形状,轧制后的钢板在厚度1/2和1/4处的性能也比表面表现出较差的性能。因此,仅仅采用压缩比来评判厚板轧制工艺的合理性是不够的,需要更进一步对厚板轧制过程轧件内部变形量的分布规律进行研究。

厚板轧制过程中,轧件内部的变形量分布,即变形渗透,引起了较为广泛的关注和研究[4-7]。与不同时期的科研条件和手段相关,目前为止,这些研究方法大致可以分为两类:

(1) 第一类方法,也是最早开始进行的方式,即通过传统的实验室试验,如在轧件边部打孔作好标记位置,或者在轧件内部布置一些网格状的金属棒,然后对轧件进行加热、轧制、冷却,再对轧后钢板边部打孔位置的迁移演变,或者钢板内部布置的金属棒的变形和位置变动进行分析,以研究钢板内部不同厚度层面上的变形量随着厚度的变化分布规律。

(2) 第二类方法,则是随着计算机和计算软件高速发展所产生,即通过有限元模拟仿真计算软件,针对厚板轧制工艺,建立相应的有限元模型,可以对一定工艺条件下的厚板轧制过程进行模拟计算,最终分析一定工艺条件下的轧件内部变形量的分布规律。该方法效率比第一类方法有明显提升,对人员有较为专业的技能要求。但是,厚板轧制工艺较为复杂,在工艺变动的条件下,上述方法常常跟不上工艺设计的效率要求。

通过查询,尚未有相关软件可以解决厚板轧制过程中变形渗透的快速计算问题。本文中所涉及到的工作,以大数据环境为背景,针对厚板轧制过程中变形渗透高效计算为目标,开发具有自主知识产权的计算用工艺设计辅助软件。开展了实现厚板轧制过程中变形渗透的定量化研究,且能够满足高效迎合生产现场以及产品研发过程快节奏的需求。采取数值模拟计算为基础,再通过python联合开发,以更好地研究、理解厚板轧制过程中的变形渗透机制。进一步,将数值研发结果导入到厚板PIDAS系统,完善PIDAS系统针对厚板变形渗透的设计辅助功能,可以为厚板产品进行轧制工艺设计优化,也开启了对自主工艺设计软件领域进行探索。

2 研究方案

2.1 数值模拟计算

针对宝钢5 m厚板厂的轧制工艺参数范围,设定轧辊辊径为φ1 200 mm,轧辊转动速度为2 r/s,轧件厚度范围为50～750 mm,道次压下范围为10～50 mm,轧制速度为2.4 m/s。图1为有限元仿真软件模拟轧制模型的建立示意图。针对上述参数条件,采用数值模拟仿真软件进行模拟,可以计算出厚度范围为50～750 mm,每50 mm为一个步长,共计15个厚度;道次压下量范围为10～50 mm,每10 mm为一个步长,共计5个压下量,在厚度方向获得变形量分布(真应变)。

中国乳制品进口价格的由乳制品的进口数量和乳制品的进口金额获得。其选取的样本区间为2006—2016年，记作ln P。

图1 有限元轧制模型示意图

图2为有限元仿真模型计算钢板在轧制后轧件内部在厚度方向获得真应变的分布云图。从云图上可以看出,钢板的变形集中在钢板上下表面的红色区域范围,而轧件厚度中心大部分范围内没有明显的变形。

通过对轧件厚度方向真应变数据提取,可以得出轧制后轧件内部在厚度方向获得真应变分布的规律。图3为厚度550 mm的轧件在压下量为30 mm的条件下厚度方向获得真应变分布的规律。为了方便后续的数据处理,厚度进行了归一化处理,即轧件上表面标示为0,钢板下表面标示为1。由此可以看出,厚度550 mm的轧件在变形量为30 mm时,只有轧件的上下表面占全厚度20%左右的区域获得了较大的有效变形量,其中间位置获得变形量微乎其微,变形渗透厚度上下表面各110 mm左右。

图2 轧制后钢板厚度方向真应变分布云图

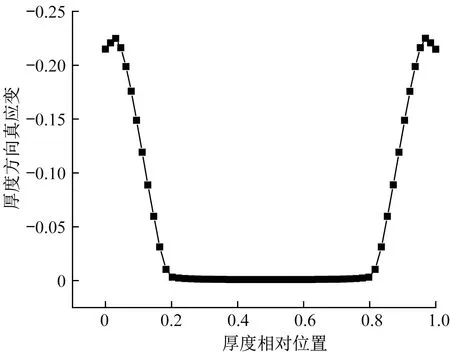
图3 550 mm厚度轧件在单道次压下量30 mm时厚度方向获得的真应变分布

通过上述方法,计算不同厚度轧件在不同压下量范围条件下轧件内部在厚度方向获得的真应变,并建立数据库。轧件厚度范围为50～750 mm,每间隔50 mm为一个步长,共计15个轧件厚度;压下量范围为10～50 mm,共计5个压下量。对所有这些参数建立相应的有限元模型,通过大量的模型计算,获得上述工况条件下的变形分布参数,并建立相应的数据库。

2.2 python编程开发

通过python编程开发,建立相关的模型,实现多功能计算功能。

(1) 用户通过输入条件,如轧件厚度(50～750 mm)、道次压下量(0～50 mm)、轧件厚度方向指定位置(0～1.0),可以查询指定轧件厚度和指定道次压下量条件下,轧件内部指定位置的真应变。

(2) 可以通过输入条件,如轧件厚度(50～750 mm)、终轧目标厚度(5～360 mm)、轧件厚度方向指定位置(0～1.0),程序可以自行分配各个轧制道次压下量,并且计算各个道次条件下指定位置的厚度方向真应变,并且可以实现各道次变形量的累加。

图4为轧件从700 mm厚度轧制到100 mm厚度钢板过程中,厚度1/2处在各道次获得厚度方向的真应变量。可以看出,当前的工艺条件下,在轧件厚度大于400 mm时,厚度1/2处只能获得较小的变形量,即无法在轧件心部实现变形渗透;在厚度小于400 mm时,变形才逐渐渗透到厚度1/2处。

图4 轧制过程中轧件厚度1/2处在各道次获得厚度方向的真应变量

图5为同一钢种、采用相同厚度的坯料,在四种不同的轧制规程下轧制后得到相同厚度的4块钢板在厚度1/2和1/4处获得的真应变累积的情况。可以看出,压下工艺编号3的钢板,其工艺条件下可以使得钢板在内部获得较好的变形渗透,而压下工艺编号1的钢板,其工艺条件下在钢板内部获得最少的变形渗透。由此证明,在初始厚度和目标厚度相同的情况下,即相同的压缩比条件下,调整压下工艺规程,可以在轧件内部获得不同的变形量累积分布。

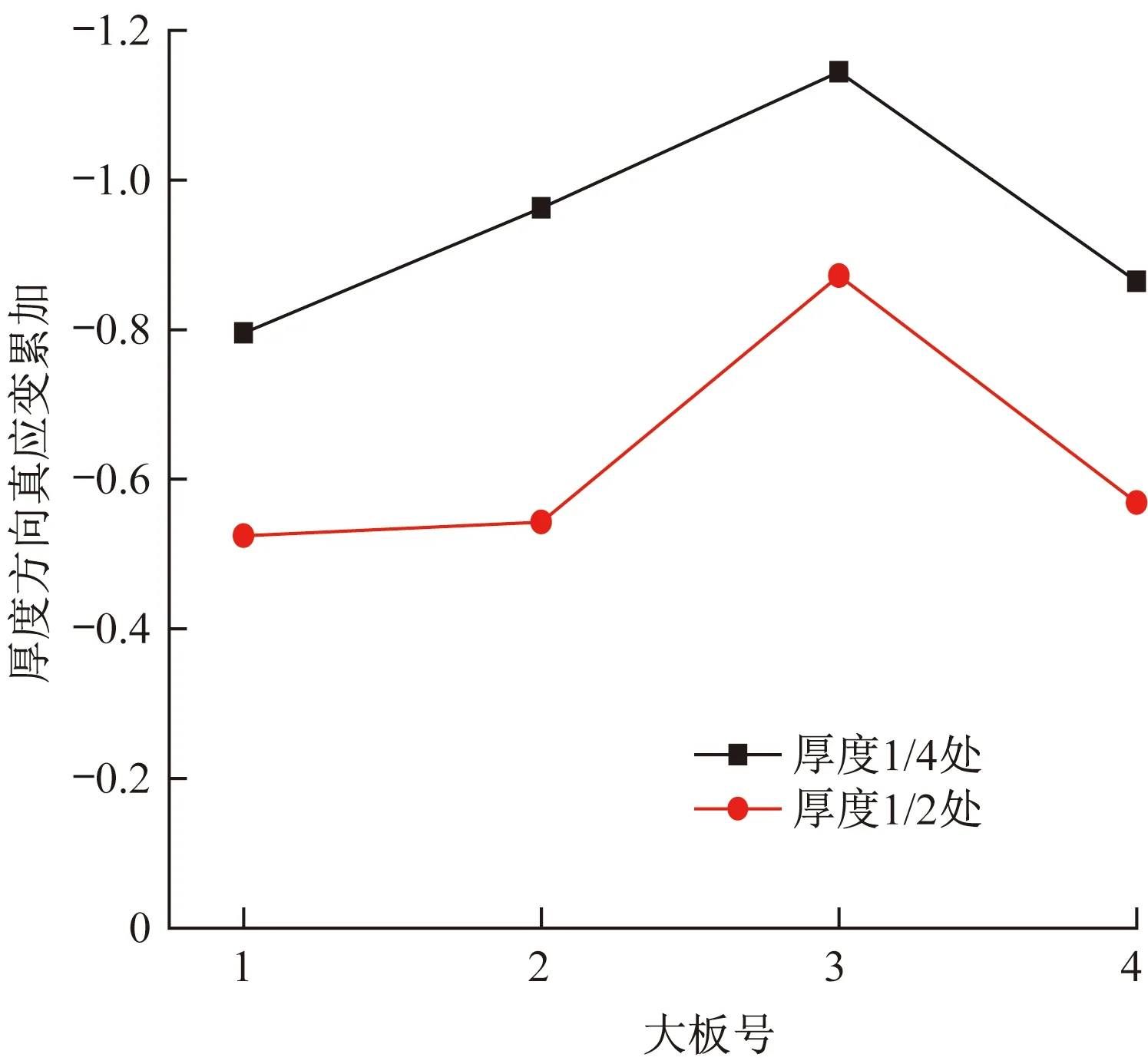
图5 同一钢种在不同压下工艺条件下厚度1/4和1/2处获得的真应变累加

2.3 PIDAS系统内钢板生产实绩进行变形渗透计算

通过PIDAS系统,调取厚板厂生产9 000张钢板的历史轧制规程记录,坯料的初始厚度为同一规格,即360 mm厚度的连铸坯,轧制目标钢板厚度为50～100 mm,压下量范围比较接近。采用本文所开发的程序进行计算,这些钢板在其轧制规程条件下对钢板厚度1/2和1/4处位置的变形渗透开展计算,并进行厚度方向的真应变累加。再调取这些钢板的压下道次数,把每张钢板的厚度1/4处和1/2处的变形累加量和道次数进行相关性分析。

图6为钢板厚度为1/2处真应变累加与道次数的关系示意图。可以看出,道次数越多,整体上各个道次的压下量就相对越少,整个工艺条件下在钢板厚度1/2处获得的真应变累加就越少。因此,减少轧制道次数、增加各个道次的压下量,可以增加钢板厚度1/2处的变形渗透。

图7为钢板厚度1/4处真应变累加与道次数的关系示意图,可以得出与图6相近的规律。通过对比图4和图5,可以看出钢板在厚度1/4处获得的变形量明显高于厚度1/2处所获得的变形量。

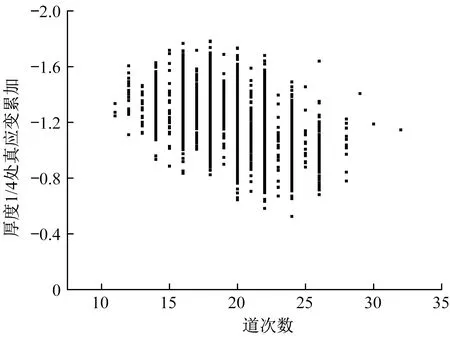
图7 钢板厚度1/4处真应变累加与道次数的关系示意图

2.4 效率提升分析

针对厚板轧制过程中变形渗透规律研究,最早通过传统实验室试验的方法,需要数周时间来完成一轮次试验并获得试验报告。

随着计算机技术的发展以及相应的商用计算软件的推出,通过单纯有限元计算的方法,根据工艺复杂性,从问题的提出到分析结果,需要数天来完成一轮次的模拟计算工作。

本数值研发工作是属于大数据背景下所诞生的成果,通过前期建立大量的有限元仿真计算获得数据库,再联合python编程开发,形成工艺设计辅助计算软件,并实现相应设计辅助计算功能,从查询条件输入到结果输出,1张钢板的工艺需要几分钟时间即可完成。从PIDAS系统查询9 000张钢板工艺到计算结果输出,需要2～3 h完成。

图8为不同研发手段的时间效率比对,从上述数据分析,本数值研发成果不但实现了钢板内部厚度方向真应变的定量化计算,而且效率得到了很大的提升。

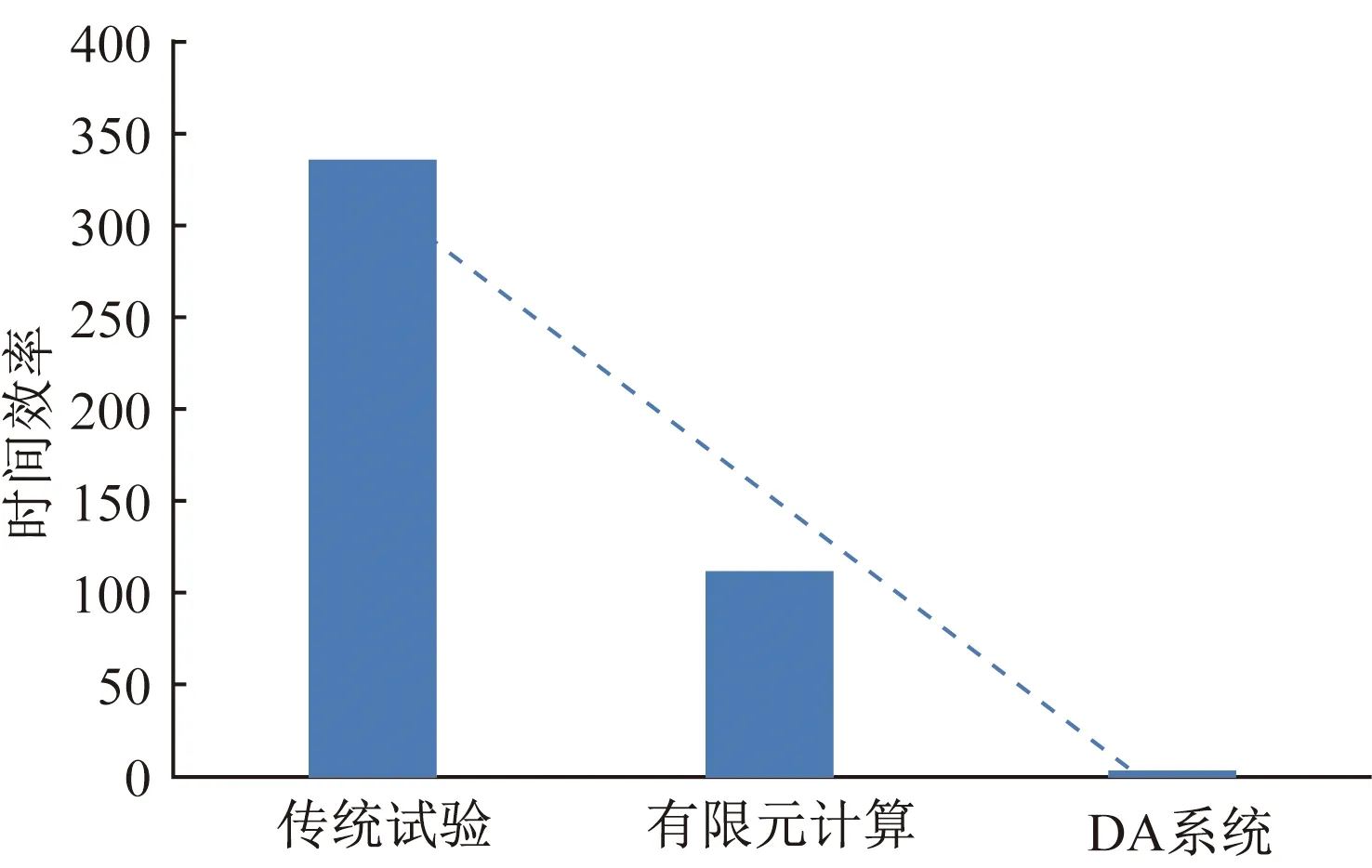
图8 不同研发手段的效率比对

3 讨论

采用有限元数值模拟计算方法模拟了厚板轧制工艺,再结合python联合开发,对厚板轧制过程中变形渗透规律进行定量化研究,克服了以往的有限元数值模拟计算方法准确度虽高但效率低的缺点,大幅度地提升了用户使用效率。如果采用传统的有限元数据模拟方法对PIDAS系统即时收集到的已生产钢板进行轧制变形计算,由于钢板生产时间远小于有限元计算耗时,传统方法根本不可能完成即时钢板计算任务。该研究方案可对其他高耗时计算方法与大数据系统的结合提供参考。

另一方面,本文介绍的厚板轧制过程轧件内部变形渗透定量化计算方法,填补了原有PIDAS系统在钢板产品虚拟试制功能上的缺失环节,使PIDAS产品设计的虚拟试制功能从基于纯数据的黑箱模型演化到大数据与轧制变形机理结合的知识模型。包括本文所介绍内容在内的产品设计辅助DA研发工作[1]正在取得不断进步,PIDAS系统正在更精细化地为产品设计流程赋能,已经可以方便地实现高效的虚拟试制来代替昂贵的实物试制,同时产品设计工程师可以非常容易地获得丰富的细粒度的各类生产实际数据、数值计算数据,进而快速提升自身的产品设计能力,加速产品研发流程。

4 结论

(1) 在厚板轧机的轧制参数范围内,当轧件厚度大于400 mm时,只能在距离钢板表面110 mm左右厚度范围内获得较为明显的变形渗透,轧件心部无法获得明显的变形渗透。当轧件厚度小于400 mm时,可以在轧件心部获得厚度方向的变形渗透,且随着轧制规程的推进,轧件厚度越小,在轧件心部获得变形量越大。

(2) 针对同一钢种,在相同压缩比的情况下,施加不同的压下工艺规程,可以明显提高钢板内部的变形渗透,从而在钢板厚度1/2和1/4处获得较多的变形量。

(3) 通过PIDAS平台,调取了9 000张钢板轧制实绩,计算了钢板内部获得变形渗透的变化规律,发现钢板内部获得变形量的多少与道次数成反比例关系。

(4) 本数值研发成果可以快速提升厚板轧制过程中变形渗透的工艺评价效率。