面向磁悬浮视触觉交互的多速率系统框架

石杰元，袁志勇，廖祥云，赵俭辉

1.武汉大学 计算机学院，武汉430072

2.中国科学院 深圳先进技术研究院，广东 深圳518055

触觉是人类赖以探索世界的重要感觉通道。如今，提供实体触觉存在许多方式，如机械[1]、超声波[2]、喷气式[3]、磁悬浮[4]。目前广泛使用的Geomagic Touch的Phantom[1]触觉设备基于机械传动方式提供触觉反馈，交互过程中受到机械关节固有摩擦、惯性的影响，且操作空间有限。基于超声波[2]、喷气式[3]的非接触触觉反馈方式消除了机械交互方式中的固有摩擦，但仍存在些许不足，例如超声波触觉设备存在力传输距离较短、对噪声敏感、存在安全隐患等问题[2]；喷气式设备由于采用空气作为力传导介质，力在压缩空气场中的传导速度较慢，且力反馈缺乏时空特性，操作空间有限[3]。基于磁悬浮的非接触式触觉反馈消除了机械交互方式中的固有摩擦，且可通过自适应调节磁感线圈电流、摆放角度等方式，实现灵活的6-DOF触觉反馈[4]，操作更加自由、稳定，具有广阔应用前景。为此，本文基于磁悬浮触觉反馈设备[4]，提出一种面向磁悬浮视触觉交互的多速率系统框架，该系统由双目视觉定位、虚拟场景物理仿真和触觉渲染三部分组成，各部分相互协同。

为确保视触觉交互过程中的视觉可信性，需构建真实可信的虚拟场景。本文采用基于位置的动力学（Position Based Dynamics，PBD）[5]作为虚拟场景的物理仿真方法。PBD相对于有限元方法（Finite Element Method，FEM）[6-7]而言，计算效率更高、实时性更强、交互性更好。此外，与传统机械定位方式不同，设备采用双目视觉定位方式。因此，需构造面向磁触觉设备的定位数据映射算法。

在磁悬浮视触觉交互中，为避免虚拟工具穿透物体，并提供稳定真实的触觉反馈，触觉渲染算法至关重要，但针对磁悬浮触觉设备[4]，现有OpenHaptics[8]触觉开发工具无法直接使用，因此需建立面向磁触觉设备的具体触觉渲染算法。在计算机触觉研究早期，绝大部分触觉渲染算法是3-DOF的，用户通过控制虚拟代理点与虚拟环境进行交互，生成3-DOF触觉反馈，经典方法包括god-object[9]、virtual proxy[10]、ray-based[11]等。以上3-DOF算法实现简单、计算效率高，但由于无法提供反馈力矩信息，适用场景有限。此后，随着触觉生成硬件不断发展，6-DOF触觉渲染算法得以出现，其以6-DOF形式记录虚拟工具运动轨迹，并且可同时提供反馈力、力矩，相较于3-DOF算法具有更高精度，但其计算复杂度往往较高。

在本文中，考虑到所使用的磁悬浮触觉设备[4]的手持触觉接口为一根底部配置小磁铁的杆状工具，充分结合3-DOF与6-DOF算法各自的优点，通过对现有3-DOF基于射线的触觉渲染方法[11]的扩展，提出一种多射线触觉渲染方法，基于力系等效原理[12]，其不仅能提供6-DOF逼真触觉反馈，有效避免工具“穿透”，同时也满足触觉刷新频率的要求。

此外，在视触觉交互场景中，图形渲染的刷新频率一般为30 Hz左右，但维持触觉渲染算法稳定需要1 kHz以上的刷新频率[13]。传统的针对这一速率冲突的解决方法主要分为两类：一是通过降低物理仿真的计算复杂度，即提高物理仿真的计算速度来满足触觉更新频率的要求，典型方法包括模态分析[14]、形变预计算[15]等，但这种简化会对仿真的真实性与稳定性造成影响。另一类为多速率方法，通过将形变仿真和触觉渲染划分成不同更新频率的并行模块，高速率触觉渲染通过捕捉低速率形变仿真的瞬态值以计算触觉反馈[16-18]。本文采用第二种方法，通过多线程并行技术实现系统不同模块间的多速率协同。

1 多速率视触觉仿真框架

1.1 系统总体框架划分

本文的磁悬浮视触觉交互系统的流程如图1所示，为方便后续描述，给出关于触觉接口的三个不同定义：（1）“视觉工具”，指代现实世界中操作者实际手持工具。（2）“触觉工具”，指代虚拟工具，其位姿通过对定位数据映射得到，不受虚拟环境障碍物的约束，可以穿透障碍物，运动趋势与用户操作动作保持同步。（3）“图形工具”，指代满足虚拟环境非穿透约束的理想工具。通常当触觉工具已穿透虚拟物体时，图形工具仍将被限制在碰撞物体表面以避免穿透。

如图1所示，整个系统为一个闭环系统。首先，用户手持视觉工具进行操作，其运动被视觉定位模块所捕捉。接着，通过映射算法，将定位数据映射到触觉工具的位姿。当碰撞检测到触觉工具与其他虚拟物体发生碰撞时，触觉渲染模块便计算触觉反馈信息，并将其传递给触觉生成硬件。最终触觉硬件生成相应的磁场，与视觉工具底部小磁铁发生相互作用，进而使用户感受到真实的反馈力，并对用户接下来的操作造成影响。上述过程便形成了一个闭环，接下来，将针对各模块展开详细介绍。

图1 系统总体运作流程

1.2 视觉工具到触觉工具的映射

视觉定位模块负责跟踪视觉工具的运动，并通过映射算法将双目视觉定位数据映射为触觉工具的位姿。接下来将对映射算法的构造展开具体论述。

1.2.1 工具位姿向量的表示

在本文系统中，触觉工具被建模成一个刚性杆，具有六自由度位姿信息，其中包含三个平动自由度和三个转动自由度。视觉工具、触觉工具的六维位姿向量定义如下：

1.2.2 位姿信息的映射方法

图2 预采样操作示意图

用户手持视觉工具在定位区域中进行任意的操作移动，其中定位区域如图2半透明长方体区域所示。通过对操作中的定位输出数据进行统计处理，便可得出视觉定位输出的大致坐标范围，类似于AABB包围盒，本文将视觉定位坐标边界范围定义为如下六维向量：其中，上标B代表边界。以的映射为例，构造映射关系如下：

其中，Lx代表触觉工具x坐标范围区间的长度，Tx代表区间左端点相对于原点的平移量。y、z坐标也以一种类似的方式进行映射。针对旋转分量的映射，由于定位模块输出数据中采用单位向量来表示杆的主轴方向，因此只需一次从单位方向向量到欧拉角的简单变换即可。至此便完成了从的映射，进一步基于刚体动力学的基本原理，可计算出触觉工具的线速度和角速度

1.3 基于位置的动力学物理仿真

视触觉交互应用需求与传统图形应用存在一定区别，尤其是针对触觉工具的仿真。在本文系统中，除触觉工具之外，其余虚拟物体均以传统PBD[5]的方式进行建模仿真，对形变特性利用体积保持约束进行建模[19]。特别地，触觉工具的位置、速度增量仅来源于视觉工具的移动，而不应拥有其他的增量来源，例如PBD中的辛-欧拉预测步[5]、碰撞约束求解导致的增量等。

1.4 多速率并行

为协调不同模块之间的运行速率差异，本文系统实现了基于CPU的多速率并行。并行模块划分策略如图3所示，三个并行模块通过共享内存双缓冲区的方式实现数据的单向流动通信，并运行在不同时态更新率上。其中，W1、W2为写缓冲区，R1、R2为读缓冲区时刻的第i个碰撞对信息为图形工具位姿向量，为对应的触觉反馈。

图3 并行模块划分示意图

1.5 多射线触觉渲染

在触觉渲染模块中，为确保视触觉交互体验可靠、真实，提升沉浸感，需要保证视觉与触觉上的双重可信性，即实时逼真的非穿透图形工具位姿计算与6-DOF触觉反馈计算[13]。

1.5.1 图形工具的位姿计算

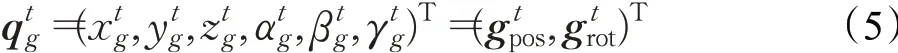
为计算qtg，首先需要考虑触觉工具与虚拟物体可能的碰撞情况。如文献[11]中所提到的，射线与凸壳物体之间的交互分为三类：（1）点-多边形交互；（2）点-边交互；（3）点-面交互。考虑到本文系统将触觉工具建模成一个刚性杆，后两种交互情况的发生概率较低，此处只考虑第一种交互：点-多边形交互。当碰撞发生时，碰撞检测算法会生成多个碰撞对信息。其中，本文碰撞检测基于符号距离场算法[20-21]实现，碰撞对信息定义如下：表示t时刻由于触觉工具碰撞所产生的第i个碰撞对信息，cph和cpo分别为触觉工具、碰撞物体表面的碰撞点，normal为cpo处的表面法线，方向指向碰撞物体外部，tangent为cpo处的单位切向向量。

在经典的基于射线的触觉渲染算法[11]中，触觉工具往往以单线段进行建模，发生碰撞时，只生成一个碰撞对，包含两个接触点，这种建模方式由于没有考虑触觉工具的具体形状而不够精确。为此，本文提出了基于多射线的触觉渲染方法，如图4所示，沿柱状工具母线建立多根射线并同时考虑多个碰撞对信息。参照文献[10，22]中关于触觉接口点（Haptic Interface Point，HIP）的定义，本文在触觉工具的底部圆周采样n个点作为HIP，并以这些触觉接口点作为射线的底部端点。定义向量Linei,j=HIPi-cpj，其中cpj为碰撞物体表面的第j个接触点。为描述方便，接下来将会省略一些下标。

图4 多射线建模示意图

本文观察到，当触觉工具穿透其他物体时，向量Line到对应碰撞对的表面法向量的投影距离必为一个负值。反之，若触觉工具没有穿透其他物体，该投影距离必为一个非负值。基于此便可利用碰撞信息，实现针对触觉工具的快速穿透检测。定义射线的符号距离dist=Line⋅normal，如果dist＜0，则判定该射线已发生穿透，否则便没有穿透。针对每条射线，对所有的碰撞对进行一次遍历，并依次计算该射线对应的dist。定义六维穿透矫正向量Δcorrt，其由3个平动矫正量和3个转动矫正量组成。因此，可如下计算：

当触觉工具未发生穿透时，矫正向量Δcorrt为一个零向量，即图形工具位姿与触觉工具位姿保持一致。当触觉工具发生穿透时，为消除穿透，应将工具往物体外部方向（物体表面法线方向）移动，基于此想法，本文将矫正向量Δcorrt定义如下：

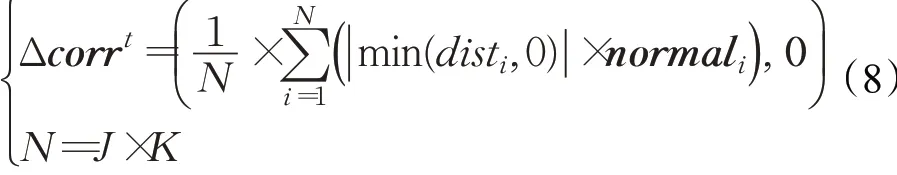
其中，N、J、K分别代表穿透距离disti的数量、射线数和碰撞对的数量。至此，便得到了矫正后的图形工具位姿，接下来将对6-DOF触觉反馈计算展开论述。

1.5.2 计算6-DOF触觉反馈

现行的6-DOF触觉反馈计算方法主要分为两类：直接渲染与虚拟耦合[13，23]。其中，在直接渲染方法中，碰撞响应直接基于穿透深度进行映射计算。在虚拟耦合方法中，其在力反馈触觉设备和虚拟触觉工具之间建立一种虚拟弹簧阻尼元件的联系，用户手部给触觉设备所施加的力也会被考虑进碰撞响应以及图形工具的位姿计算之中。由于本文的磁悬浮视触觉交互系统采用非接触式的操作方式，无法对用户操作所施加力的具体大小进行捕获，因此本文将采用直接渲染方式来实现6-DOF触觉反馈计算。

在交互过程中，尽管用户手部位置、视觉工具的空间绝对位置、工具底端与握点的相对位置会随着操作的进行而不断变化，但用户手与工具握点的相对位置将始终保持不变。因此，可采用球型铰链作为交互工具的力学模型，将握点建模成球形铰点，如图5所示。

图5 触觉接口力学模型

由于小磁铁位于视觉工具底端，因此触觉反馈力作用点也将为工具杆底端。图5中，F表示触觉反馈合力，M表示相对于铰点O的反馈合力矩。基于力系等效原理，可将合力矩M等效转换为作用在杆底端的力FM。进一步对F和FM进行平面正交分解，并将对应方向的分力进行合成，便可得到如图5右半部分所示的最终两个正交力：Frot和Fparallel，其中，一个垂直于杆，一个沿杆方向，这两个力将分别为用户提供“旋转”和“轴向阻碍”的感受。与图形工具位姿计算方式相对应，触觉反馈如下计算：

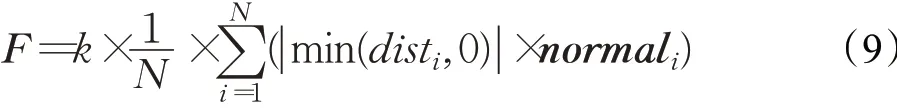
其中，rod为杆主轴的单位方向向量，k、kparallel、krot为三个刚度调节系数，分别用以调节触觉反馈的整体强度、轴向阻力强度和旋转反馈强度。通常，设置k=C、kparallel=krot=1，其中常数C根据触觉设备输出力的范围进行确定。在本文应用场景下，利用Frot和Fparallel来替代F和Μ将不会产生任何操作感受上的差异。

2 实验仿真与评估

实验中操作者通过操控磁悬浮触觉反馈设备[4]与虚拟场景进行交互，本文对刚体碰撞、刚体-形变体碰撞交互进行了实验仿真，并完成了相应的触觉渲染计算。其中，虚拟场景基于PBD框架[5]进行扩展构建，重点利用PBD框架的物理仿真与碰撞检测机制。由于视触觉交互应用场景需求的特殊性，触觉工具的移动将仅由用户操作决定，为此实验移除了虚拟环境中的重力，从而保证不存在用户操作输入时，触觉工具能够在自由三维空间中保持静止。

通常在虚拟外科手术应用中，为获得特定的模型（例如患者的肝脏模型），需要基于一系列肝脏医学图像进行三维重建，再利用网格生成技术生成最终的仿真三维模型。但这不是本文核心工作所在，本文首先从一些开源模型数据集上取得三角面片模型，之后利用模型处理软件（如Maya）对模型进行减面简化，进而对简化模型利用开源软件Tetwild[24]进行四面体体素化，最终得到用于物理仿真的四面体网格。

2.1 刚体交互场景仿真

在刚体交互场景中，构造触觉工具与刚性地面之间的碰撞场景如图6所示，其中灰色部分代表刚性地面，蓝色杆代表触觉工具，橘黄色杆代表触觉渲染算法计算出来的图形工具，世界坐标系的x、y、z轴分别以红、绿、蓝细线表示。在此场景中，用户手持视觉工具以控制虚拟触觉工具慢慢穿透刚性地面。当触觉工具未与地面发生碰撞时，图形工具与触觉工具的位姿保持一致，两者相互重合。随着触觉工具的不断下移，其与地面的穿透量也逐渐增大，而图形工具始终保持在地表从而有效避免了穿透，与之相应的触觉反馈力变化也如图7所示。

图6 刚体碰撞场景

图7 刚体碰撞场景的触觉反馈

在该过程中，随着穿透不断加深，反馈合力、分力的幅值也不断增大，由于此时主要为Y方向上的移动，因此Y分量占据了合力的主要部分，该生成结果在触觉上也是合理的。

2.2 形变体交互场景仿真

实验对触觉工具与形变体之间的交互也进行了仿真。在这些场景中，为了观察形变模型特定区域的形变，对模型的部分无关区域进行了固定处理，例如针对犰狳模型的四肢进行了固定。如图8所示，当触觉工具与柔性犰狳进行交互时，犰狳发生了适当的形变，同时图形工具始终保持在犰狳的表面，有效避免了穿透。同样地，与该交互过程相对应的触觉反馈力也在图9中给出。由于用户操作主要是Y方向由上至下的与犰狳的碰撞交互，因此合力的Y分量将相对于X、Z分量具有更大的变化范围。此外，由于犰狳的形变特性，在碰撞点处会发生凹陷，导致碰撞处法线方向与杆的主轴方向十分接近，平行分力的幅度远远大于垂直分力，不过在实际操作过程中，垂直分力的大小也可通过刚度参数krot来进行调节。

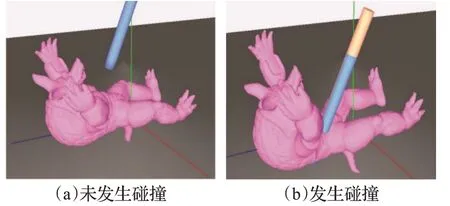
图8 犰狳碰撞场景

图10 、图11分别展示了针对形变肝脏和形变斯坦福兔子的交互仿真场景，可见本文触觉渲染算法也有效地避免了穿透，并伴随与之对应的可信视觉形变。

图10 形变肝脏碰撞交互

图11 形变兔子碰撞交互

当所有模块以串行顺序运行（即视觉定位-物理仿真-触觉渲染的顺序），场景中的形变模型三角面片数为30 000、四面体数为3 717时，一次完整的串行流程计算需要31 ms，对应32 Hz的刷新率，远低于1 kHz的触觉刷新率要求。而将系统实行并行模块划分之后，触觉渲染模块仅需0.13μs即可完成一次更新，满足1 kHz的速率要求，相应的测试结果在表1中给出。

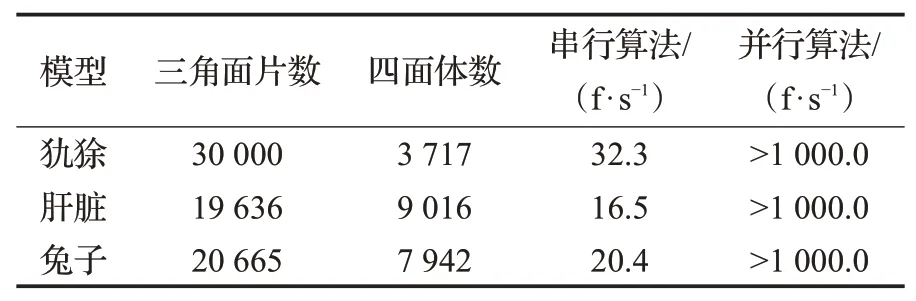
表1 串行、并行算法力更新频率比较

3 结束语

本文提出了面向磁悬浮视触觉交互应用的多速率系统仿真框架，该系统能够满足稳定、高效的视触觉交互需求，且相对于传统机械交互方式，系统采用非接触的操作方式，具备更多的操作自由度且消去了摩擦。系统对传统3-DOF单射线触觉渲染方法进行了扩展，基于力系等效原理，可以为用户提供6-DOF触觉感知。实验结果证明本文方法可以有效避免不真实的穿透以及提供真实、合理的视触觉反馈。

然而，本文还存在一些不足。目前实验假定仿真模型是各向同性的，后续将针对各向异性的生物力学参数模型进一步开展实验。此外，由于触觉渲染线程基于物理仿真线程的瞬时配置进行计算，触觉反馈结果的不连续性将在一定程度上受限于物理仿真线程实际刷新的速率，未来将继续探索针对这一速率差异的误差补偿方法，以降低触觉反馈结果的不连续性。