提高卫星导航精度的卡尔曼滤波算法应用研究
2021-03-09岳崇伦郭云开
岳崇伦,曾 苑,郭云开,2
(1.广州城建职业学院,广东 广州 510900;2.长沙理工大学 测绘遥感应用技术研究所,湖南 长沙 410076)
汽车、火车、轮船等交通运输工具在人们的日常生活中扮演着不可或缺的角色,它们的速度是体现它们性能的重要指标之一,如何测量它们的速度现在已经有很多方法,而如何提高测速精度是现在研究的重点。对于海上行驶的交通运输工具来说,精确测量它们的速度更加难,大海上没有参照物,也不可能架设雷达等设备,因成本太高。
2020 年 6 月全面建成的北斗三号系统将为全球用户提供授时、定位导航、全球短报文通信和国际搜救服务,同时可为中国及周边地区用户提供星基增强、地基增强、精密单点定位和区域短报文通信等服务。北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)作为着眼于国家安全和经济社会发展需要的国家重要时空基础设施,是中国战略性新兴产业发展的重要领域。BDS 已成为联合国卫星导航委员会认定的全球四大导航系统之一。相比于 GPS 的信号可靠性不能充分保障、易受“干扰”等弊端,BDS 具有抗遮挡能力强、服务精度更高、服务能力更强等特点。随着我国卫星事业的发展,其应用功能和性能有很大提高空间[1]。交通运输部表示,2020年将在交通运输系统的道路客运车辆、城市里的配送车辆、公交车、长江干线的船舶以及飞机、火车全面推广使用北斗卫星的应用。北斗三号系统的建成推进了卫星导航定位在汽车、火车、轮船等交通运输工具中的广泛应用。
海上航行用的定位方法几乎都是卫星导航,卫星导航不但可以进行定位,还可以进行测速。卫星导航系统在测速方面的应用已经十分广泛,尤其是在海上航行时,卫星导航是测量轮船速度最好的方法,因此卫星导航测速广泛应用于航海。目前应用于轮船动态测速的方法[2]主要以基于GPS动态测速方法为主,包含GPS多普勒频移测速和GPS差分测速,但都存在一定不足,这两种方法测速准确性有待提高。然而,卫星导航测速是存在误差的,这些误差一般都是偶然误差,而且当物体低速行驶时,误差更明显。卫星导航接收机显示的速度一般都包含噪声,这些噪声是随机的,属于高斯白噪声,如何消除或减少这些噪声是当前研究的重点。卡尔曼滤波[3]对于消除高斯白噪声是一种很好的方法,对于提高卫星导航测速精度有很好的效果。为此本文提出了利用卡尔曼滤波算法消除或减少噪音以提高卫星导航测速精度,并进行实验验证。
1 卡尔曼滤波
卡尔曼滤波是基于状态空间方法的一套递推滤波算法,在状态空间方法中,引入了状态变量的概念。卡尔曼滤波模型包括状态向量和观测向量,状态向量每时每刻都在变化,这种变化可以用一个方程表示,而观测向量也可以用一个方程表示,这两个方程就组成了卡尔曼滤波模型。卡尔曼滤波首先通过状态转移方程预测下一个状态,再根据观测变量来得到系统的最优估计[4-7]。
用一幅简单的流程图来表示卡尔曼滤波工作的基本流程,见图1。

图1 卡尔曼滤波工作的基本流程图
2 卡尔曼滤波在提高卫星导航精度的应用
卫星导航接收机可以实时接收卫星信号,计算出船舶的速度。但由于导航卫星播发的信号存在噪声干扰,加上海上情况复杂多变,卫星导航接收机计算的速度含有噪声数据,为了提高卫星导航测速精度,需对数据进行滤波处理,卡尔曼滤波是最好的方法[8-10]。
2.1 卡尔曼滤波模型的建立
假设船舶在n-1时刻的速度为v(n-1),n时刻船舶速度为v(n)。n-1到n时刻的时间间隔为T,T=1 s,由于时间间隔T很小,因此可假设船舶在n-1到n时刻的加速度恒定为a(n-1),则船舶在n时刻的速度表达式为:
v(n)=v(n-1)+a(n-1).
(1)
船舶在n时刻的加速度表达式为:
a(n)=u(n)+w(n).
(2)

下面定义状态矩阵:
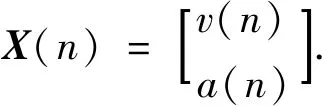
(3)
式中:v(n)表示船舶在n时刻的速度,a(n)表示船舶在n时刻的加速度,将式(1)和式(2)代入式(3)可得卡尔曼滤波状态方程:


F·X(n-1)+U(n)+W(n) .
(4)
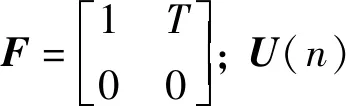
设卡尔曼滤波的测量方程为:
Y(n)=H·X(n)+R(n).
(5)
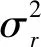
可得卡尔曼滤波模型为:
X(n)=F·X(n-1)+U(n)+W(n),
(6)
Y(n)=H·X(n)+R(n).
(7)
到此卡尔曼滤波模型已经建立,根据模型得出卡尔曼滤波器5个方程:
状态预测方程:
X-(n)=F·X(n-1)+U(n);
(8)
协方差预测方程:
P-(n)=F·P(n-1)·FT+Q;
(9)
滤波增益方程:
K=P-(n)·HT(H·P-(n)·HT+R)-1;
(10)
状态更新方程:
X(n)=X-(n)+K(Y(n)-HX-(n));
(11)
协方差更新方程:
P(n)=(1-K·H)P-(n).
(12)
2.2 实验数据和卡尔曼滤波参数
在卡尔曼滤波模型中,只需已知测量数据Y(n),船舶在n时刻的系统加速度u(n),初始状态数据X(0)和初始协方差矩阵P(0),系统噪声协方差矩阵Q,观测噪声R,通过迭代求出最优解。
一艘轮船在海上行驶,船上安装卫星导航接收机,卫星导航接收机实时显示每一秒轮船的速度(单位为海里),记录下轮船在一段时间内每秒的速度。记录的数据见表1轮船速度测量值表。

表1 轮船速度测量值表

确定观测噪声R,虽然卫星导航接收机计算出来的速度有误差,但误差不会太大,通过大量数据分析表明,观测数据误差不会超过1,因此可得观测噪声R=1。
接下来确定初始值,初始状态数据的第一个量用第一个速度值表示,第二个量为0,因此可以确定初始状态数据

2.3 Matlab仿真程序
本文的Matlab程序是在Matlab 7.0上编写和运行的。Matlab代码:
X=[0.480; 0]; %状态初值
P=[1 0; 0 1]; %状态协方差矩阵
F=[1 1; 0 0]; %状态转移矩阵
Q=[0,0;0,1]; %状态转移协方差矩阵
H=[1 0]; %观测矩阵
R=1; %观测噪声方差
Y=[ 0.480,0.470,0.460,……];%观测数据,完整数据见表1
Z= zeros(1,120);
U=[0;0];%加速度初值
for i=1:120
if i>=2
U= [0;Y(i)-X(1)];
end
X_ = F*X+U;
P_ = F*P*F'+Q;
K = P_*H'/ (H*P_*H'+R);
X = X_+K*( Y(i) -H*X_);
P = ( eye(2) -K*H)*P_;
Z(i)=X(1);
End
figure;
hold on;
T=1:120;
plot(T,Y);%画出观测值图形
figure;
hold on;
plot(T,Z); %画出滤波值图形
figure;
hold on;
plot(T,Y);
plot(T,Z,‘r’); %画出观测值与滤波值
figure;
hold on;
plot(T,Z-Y); %画出观测值与滤波值之差图形
2.4 实验结果分析
观测数据对应的折线图如图2所示,由图可明显的看出有几个数据跳跃十分大,这显然是不合理的,可以将这些数据称之为噪声数据,卡尔曼滤波可以很好的处理这些数据。经过卡尔曼滤波处理后得到的数据如表2所示。

表2 轮船速度滤波后数据表
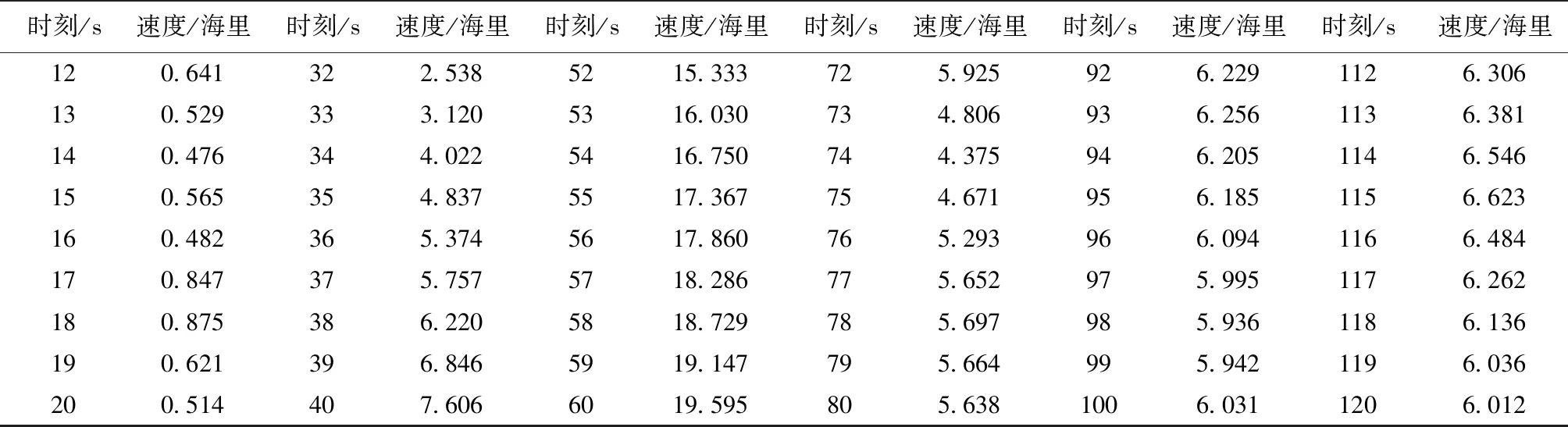
续表2
轮船速度滤波后的值对应的折线图如图3所示,很显然在图2中跳跃很明显的数据已经趋于平缓,卡尔曼滤波有了效果。

图2 轮船速度测量值

图3 滤波后轮船速度值

图4 轮船速度测量值与滤波后速度值比较图
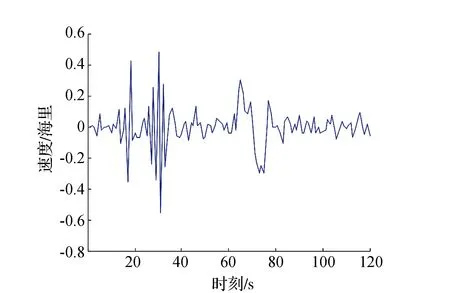
图5 轮船速度测量值与滤波后速度值之差
观察表1的观测数据,在26 s、27 s、28 s、29 s、30 s、31 s、32 s、33 s、34 s这些时刻的数据为1.110海里、1.720海里、1.280海里、2.230海里、1.310海里、2.660海里、2.270海里、3.380海里、4.060海里,这些数据跳跃十分大,很明显有些数据是噪声数据,经过滤波后,这些数据变为1.244海里、1.484海里、1.539海里、1.888海里、1.794海里、2.108海里、2.538海里、3.120海里、4.022海里,可以看出,这些数据变得更加平滑,更加准确。
综上,卡尔曼滤波提高对船舶卫星导航测速精度有很大效果。
3 结束语
本文实验测出了一艘轮船在海上一段时间内行驶速度,受外界因素的干扰,卫星导航测速得到的数据含有噪声数据,本研究用卡尔曼滤波对含有随机噪声的数据有很好的过滤效果。通过卡尔曼滤波器对测出的数据进行估计,得到相对更精确的数据;通过对比滤波前、后的数据,可明显看出滤波后的数据更精确,因此卡尔曼滤波对提高卫星导航精度效果比较理想。北斗作为我国的重要战略性技术,从长远看基于BDS的时空信息服务是智能导航的一个重要基础组件,实现卫星导航中的时空信息服务“无处不在,需则可用”是大势所趋。随着BDS的发展,卫星导航行业的应用场景挖掘是一个很重要的发展方向。在统一规划时空信息服务支撑框架基础上,提高服务精度寻求恰当的应用场景是BDS切实助力导航技术发展的关键。
