波流联合作用下通载浮桥动力特性研究

苗玉基，陈徐均，叶永林，施 杰，黄 恒

（1.陆军工程大学野战工程学院，南京210007；2.中国船舶科学研究中心，江苏无锡214082）

0 引 言

浮桥作为一种水上交通通道，一般通过锚链或钢缆将其系泊固定，以确保其能够在水流和风浪作用下顺利通载。通载浮桥的运动响应、系泊力等动力特性受到了国内外学者的关注，模型试验[1]、实桥试验[2]和数值计算[3]是研究通载浮桥动力特性的主要方法。陈徐均等[1]开展的模型试验发现通过浮桥的荷载重量越大、荷载速度越快，位移波的堆积效应越明显，基于传递矩阵法的数值计算[4]同样表明位移波的堆积主要受荷载重量和移动速度影响。此外，带式浮桥的运动响应，特别是竖直向上的运动响应对移动荷载速度更为敏感[5]。将浮桥简化为一弹性梁模型是一种有效的数值计算方法[6-7]，该方法可考虑弹性变形、移动荷载速度等对浮桥运动特性的影响。Raftoyiannis等[8]提出了可考虑接头力的浮桥动力学方程，对移动荷载速度、波浪特性等因素对铰接浮桥动力特性的影响进行了计算分析；Viecili等[9]根据浮桥的实际使用需求，对一双轴移动荷载作用下的带式浮桥进行了水槽试验，研究了荷载重量和移动速度对浮桥竖向位移的影响；王欢欢等[10-11]利用非线性显式动力学软件LS-DYNA，分析了囊式浮桥在移动载荷作用下的动力响应问题；Sun等[12]对一新型带气囊式浮桥进行了水池试验和三维水弹性计算，研究了桥节接头、系泊系统等因素对浮桥弯矩分布的影响；Chen 等[13]对一箱型桥节进行了水池试验和数值计算分析，研究了波浪参数等对桥节运动特性和系泊力的影响；Wei 等[14]提出了非均匀波浪对曲线浮桥的水弹性时域分析方法，指出非均匀波浪对浮桥的动力响应具有一定影响；Cheng等[15]对风浪流作用下的曲线型浮桥进行了数值计算，分析了风浪流对不同自由度动力特性的影响；苗玉基等[16]对复杂海底地形条件下的浮式栈桥进行了水池试验和数值计算，研究了地形条件、水深及浪向等因素对浮式栈桥运动特性的影响；Kvåle 等[17]采用有限元法和势流理论建立了流固耦合模型，对一箱型浮桥的随机动力响应进行了研究。

以上研究大多集中在单独研究移动荷载或波浪对浮桥运动响应的影响，很少关注波流环境中通载浮桥的运动响应，对通载浮桥系泊力的研究也鲜有报道。本文利用势流理论及波浪绕射/辐射理论对浮桥所处流场的速度势进行分析，采用莫力森公式计算浮桥受到的水流阻力，同时考虑移动荷载对浮桥动力特性的影响，建立了系泊浮桥在波浪、水流及移动荷载联合作用下的时域运动方程，并且在时域计算中考虑瞬时湿表面变化引起的桥节非线性浮力和水阻力，从而研究波浪、水流及移动荷载等参数对系泊浮桥动力特性的影响，为浮桥通载能力评估、系泊系统设计提供技术支撑。

1 计算原理

1.1 坐标系

为了方便后文分析，建立固定坐标系OXYZ，如图1所示，坐标原点O位于静水面上，Z轴竖直向上指向天空且坐标系为右手系。为了分析浮体的运动，建立运动坐标系o'x'y'z'，该坐标系初始时刻与固定坐标系重合，随后以浮体的水平运动速度U移动，且在移动时坐标轴始终与固定坐标系坐标轴平行，因此在分析时可作为浮体运动的参考坐标系。另外建立随体坐标系oxyz，其中坐标原点o为浮体重心G，初始状态各坐标轴与固定坐标系OXYZ各轴平行。浪向角为沿OX方向逆时针旋转至波浪前进方向所得夹角，流向与浪向一致。车辆各轴压作为多个集中荷载mi作用在浮桥桥节上，如图1所示。

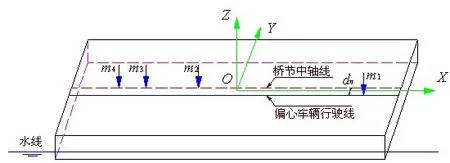
图1 坐标系Fig.1 Coordinate system

1.2 多浮体运动方程

可验证上述入射波速度势已满足控制方程，以及自由面及海底边界条件。而绕射波速度势及辐射速度势可通过格林函数法求解由控制方程和边界条件构成的速度势定解问题，从而获得绕射势和辐射势[19]。在得到流场速度势后，可进一步求得一阶波浪力及浮体的水动力系数。由于频域计算得到的附加质量和辐射阻尼是随波浪圆频率而变化的，因此采用卷积积分形式建立浮体的时域运动方程[19]：

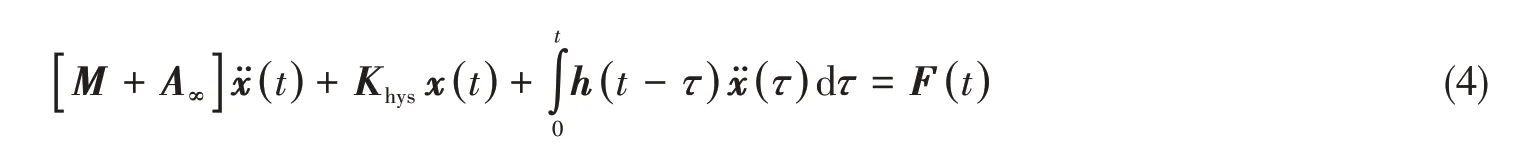
式中，M为浮体的质量矩阵，A∞为浮体的附加质量矩阵，Khys为浮体的静水恢复力阵，x为浮体的运动位移列阵，F(t)为浮体受到的外部激励力列阵，包括波浪力、水流力、系泊力、接头力及车辆荷载等；h为延迟函数，可由下式确定：

式中，A(ω)、B(ω)为由频域计算求出的附加质量和辐射阻尼，其与波浪圆频率有关。

1.3 外部荷载计算

浮桥各桥节在车辆通过时吃水会发生变化，导致水阻力也会发生改变，因此需要考虑瞬时湿表面变化的影响。本文采用莫力森公式计算浮桥水阻力，水阻力由流体质点与浮体间的相对速度确定，浮桥桥节一个微段的水阻力可由下式得到[15]：

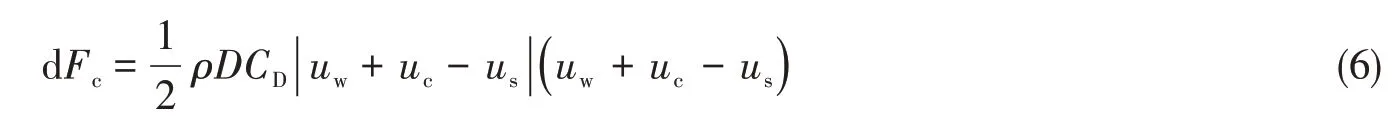
式中，ρ为流体密度，D为浮体特征宽度，随吃水深度而变化；uw为波浪速度，uc为水流速度，us为浮桥微段速度，CD为阻力系数，本文中取Cdx=1.0，Cdy=0.4，Cdz=4.8[20]。计算得到浮桥桥节一个微段的水阻力后，沿着桥长方向进行积分，即可得到该桥节受到的水阻力。

采用钢缆对浮桥进行系泊，可采用悬链线模型计算系泊力[13]：

式中，T为系泊缆张力，H为系泊缆水平力，V为系泊缆竖向力，AE为系泊缆刚度，w为系泊缆单位重量，L为系泊缆未张紧时长度，Z为系泊点竖向坐标。

车辆每个轴载以集中力的形式加载到浮桥桥节上，如图1所示。车辆荷载包括竖向荷载FVz，水平力矩FVMy，若车辆偏心通过浮桥则还需要考虑由偏心距引起的横向力矩FVMx，浮桥桥节受到的车辆荷载如下：

式中，mi为第i个车轴重量；li为第i个车轴距离桥节重心的距离，在重心前侧取正值，在重心后侧取负值，其由时间和车辆行驶速度确定；N为位于该桥节上的车轴总数；mj为第j个偏心行驶车轴重量；dVj为第j个偏心车轴与桥节中轴线之间的距离，在桥节左舷取负值，在右舷取正值；P为该桥节上偏心通行的车轴总数。

2 数值模拟方案

2.1 数值计算模型

图2 浮桥布置图Fig.2 Layout plan of the floating bridge

本文研究对象是一个由15节河中舟和2节岸边舟作为浮桥桥节组成的长浮桥，如图2所示，浮桥全长132.2 m，宽8.3 m，车行道宽6.5 m，浮桥工作水深假定为15.0 m，桥节水线位置宽度约为6.75 m。其中河中舟和岸边舟均是由两个方舟和两个尖舟构成，如图3 所示，其主要参数见表1。桥节间通过铰接接头连接，在桥节甲板处有承压块，车辆荷载通过时承压块会抵紧，防止桥节出现较大相对纵摇角。根据浮桥布置环境，浮桥河中舟部分采用垂直于桥节的钢缆系泊，系泊缆与桥节纵中轴线夹角为±90°，每个河中桥节均设置有1 根上游系泊缆，间隔一个桥节设置1 根下游系泊缆，同时岸边舟及靠近岸的一节河中舟采用斜张纲进行系泊，如图2所示。河中桥节系泊点位于桥节中点处，在桥节甲板面上距离桥节边缘为0.2 m，通过系缆桩系固，锚碇块距离桥节79 m，系泊缆详细参数见表2。沿车辆行进方向对浮桥桥节进行编号，依次为P1、P2、P3、…、P17。

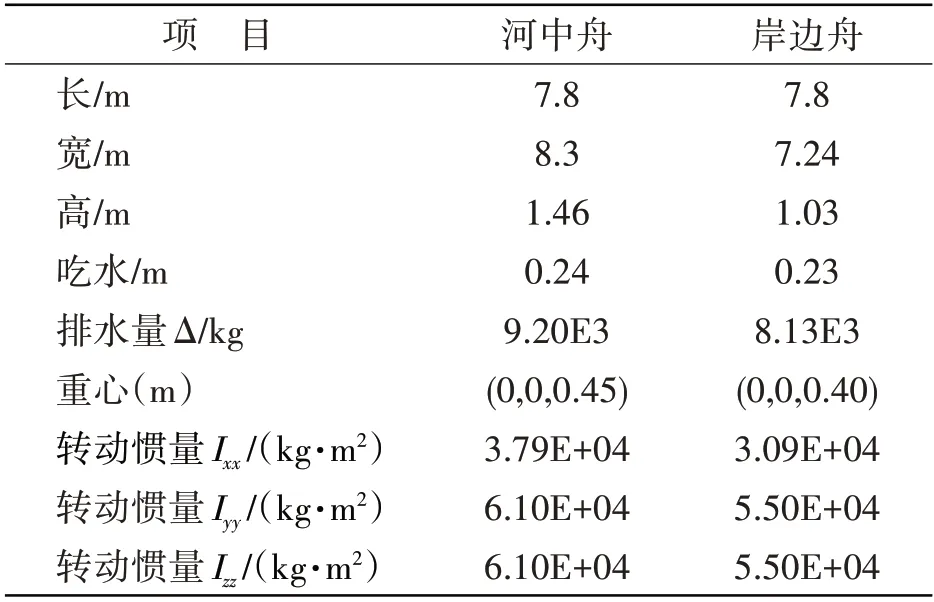
表1 桥节参数Tab.1 Parameters of the pontoon of floating bridge

表2 系泊缆参数Tab.2 Parameters of mooring lines

2.2 数值求解方案

本文采用有限元软件ANSYS/AQWA 建立系泊浮桥三维数值模型，如图4所示。每一时间步各桥节受到的车辆荷载采用Matlab 编程计算得到，然后作为外荷载文件加入到时域求解中。进而采用AQWA-NAUT 对浮桥进行时域计算分析。其中车辆荷载为5 轴轮式车（LT-60），如图5 所示，车辆总吨位为60 t，5个轴载分别设定为7.0 t、12.5 t、12.5 t、14 t和14 t，车轴间距分别为3.5 m、1.4 m、8.5 m和1.4 m。假定车辆以恒定速度沿浮桥中轴线行驶，因此未产生偏心荷载，此外，由于是恒定速度行驶，因此未考虑由车轮摩擦产生的水平荷载。计算中波浪采用二阶斯托克斯波，波幅分别为0.1 m、0.3 m和0.5 m，波浪周期为3.0 s，浪向为270°，水流速为1.5 m/s，流向为270°，车辆行驶速度为10 km/h、20 km/h、30 km/h和40 km/h。

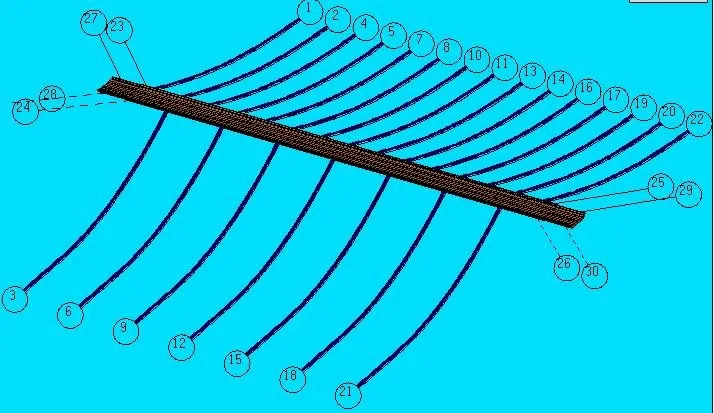
图4 浮桥三维数值模型Fig.4 3-D numerical model of the floating bridge

3 计算结果与分析

3.1 车辆行驶速度对浮桥动力特性的影响

为了研究车辆行驶速度对浮桥动力特性的影响，本文对仅有水流作用下的通载浮桥进行了计算，计算中车辆行驶速度分别取为10 km/h、20 km/h、30 km/h和40 km/h，水流速度为1.5 m/s，流向为270°。图6 对比了不同行驶速度下桥节P3、P5、P9 和P12 重心处垂向位移时程曲线。由图6 可知，各桥节垂向位移谷值深度均随行驶速度增大而增大，同时桥节垂向位移在荷载通过时会出现一个明显谷值，在荷载通过后则出现不同程度的峰值，而峰值随行驶速度增大而增大，这与临近桥节通载及位移波堆积有关。由图6（a）～（b）可知，当行驶速度为10 km/h 时，桥节P3 和P5 垂向位移在达到最小值过程中出现了多个峰谷值，这是由于5 个轴压依次加载或离开该桥节导致桥节受到的竖向荷载FVz发生变化引起的；车速提高后，5 个轴压间隔时间缩短，浮桥桥节来不及响应，因而高速通载时垂荡时程曲线较为光滑。由图6（b）～（d）可知，浮桥中段及后段桥节会出现位移波堆积现象，行驶速度越大位移波堆积现象越明显[1]，但前段桥节位移波堆积现象并不显著，这是由于位移波未能在前段桥节产生堆积效应。

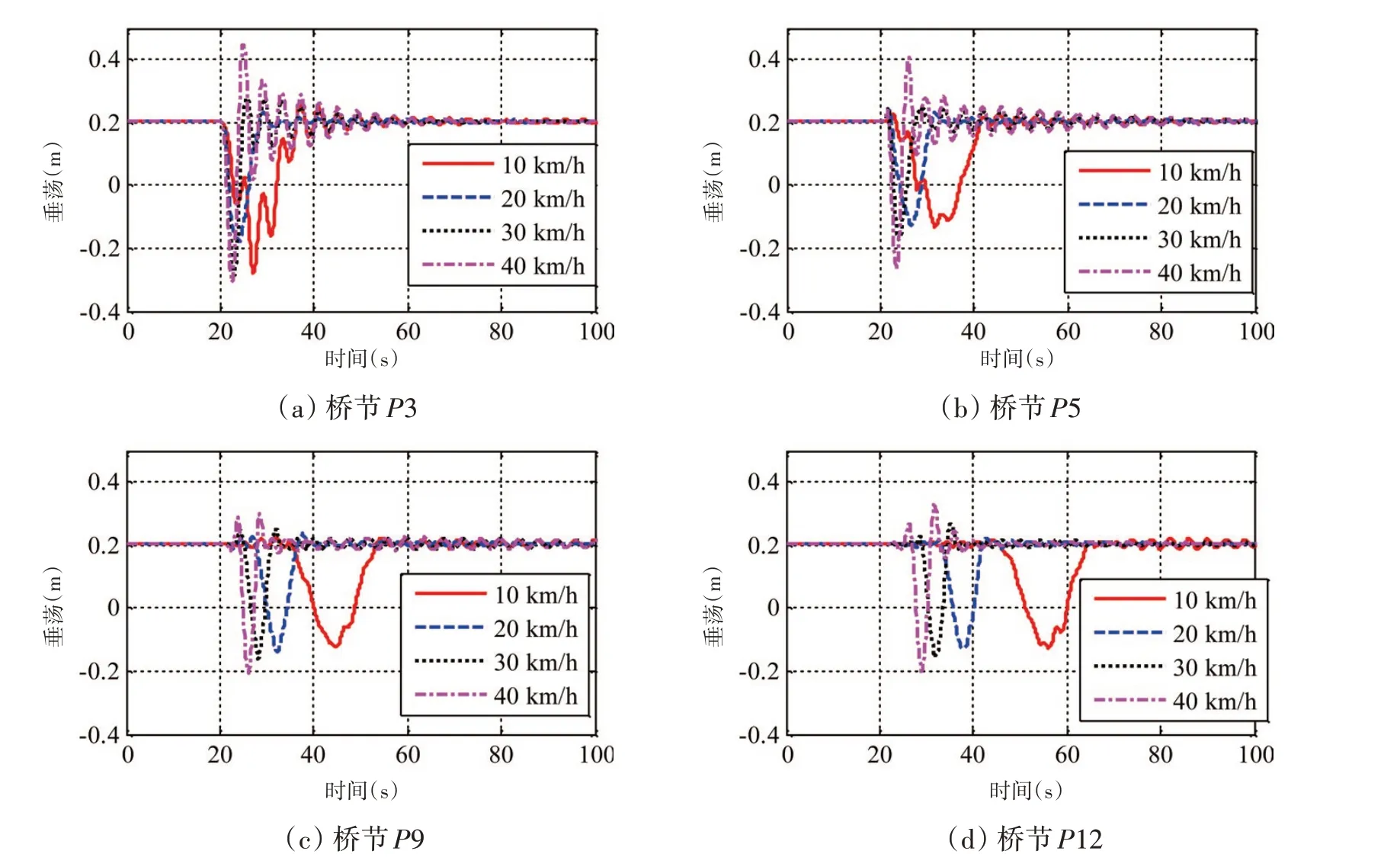
图6 不同行驶速度下浮桥桥节垂荡响应时程曲线对比Fig.6 Comparison of heave response time-history curves of floating bridge pontoons under different vehicle speeds

图7 为不用行驶速度下浮桥桥节P3、P5、P9 和P12 的纵摇响应时程曲线。由图7 可知，在车辆通过某桥节时会引起该桥节产生较大的纵摇响应，且纵摇响应峰谷值随行驶速度增大而增大。由于行驶速度不同，导致车辆到达同一桥节时的时刻不同，因此产生纵摇幅值明显变化的时刻不同，同时产生纵摇变化的时间跨度也不同。在车辆通载过程中，各桥节纵摇响应的峰值和谷值大小相近，总体上呈现对称特性。

图7 不同行驶速度下浮桥桥节纵摇响应时程曲线对比Fig.7 Comparison of pitch response time-history curves of floating bridge pontoons under different vehicle speeds

图8 为不同行驶速度下浮桥各桥节的垂向位移对比，图中对比了当车辆第1 个轴压到达浮桥第9 个桥节（P9）时各桥节的垂向位移幅值，图中横坐标为桥节序号，纵坐标为各桥节垂向位移值。由图8 可知，行驶速度对全桥桥节均具有一定影响，桥节垂向位移值随着行驶速度的增大而增大，在车辆以高速通载时更为明显，这是由于车辆高速通过浮桥时会激起较为明显的振荡效应，这也是激起如图6 中速度为40 km/h 时桥节的垂向位移呈现出更明显的位移波堆积效应的原因。

图9 为车辆不同行驶速度下浮桥桥节上游系泊缆张力时程曲线，桥节P5 上游系泊缆编号为7，桥节P9 上游系泊缆编号为11（见图4）。由图9可知，不同桥节的上游系泊缆张力峰值均随车辆行驶速度增大而增大，这与浮桥桥节垂荡响应谷值深度随行驶速度增大而增大有关，因为垂荡谷值越小桥节湿表面积越大，桥节受到更大的水阻力。同时由图9 可知桥节P5 和P9 的系泊力在车辆驶上浮桥时即开始逐渐增大，并且随之出现了多个峰值，这是由于车辆行驶到相邻桥节时会引起桥节P5 和P9 产生一定幅度的垂荡及纵摇运动，由图6（b）～（c）和图7（b）～（c）展示的垂荡和纵摇时程曲线可看出，在导致桥节吃水深度变化的同时，也导致桥节上的系泊点位置出现变化，进而引起系泊力变化。车辆行驶速度为10 km/h时，图9（a）所示的桥节P5的系泊力在大值附近震荡的时间持续了30 s 左右，此时车辆行驶到第11 个桥节，而图9（b）显示的桥节P9的系泊力在大值附近震荡的时间持续了47 s左右。这是由于桥节P9位于浮桥中段，车辆通过两侧桥节时均会对其产生一定影响，因此系泊力幅值增大持续时间较长，而两侧的桥节仅受到附近桥节的影响。

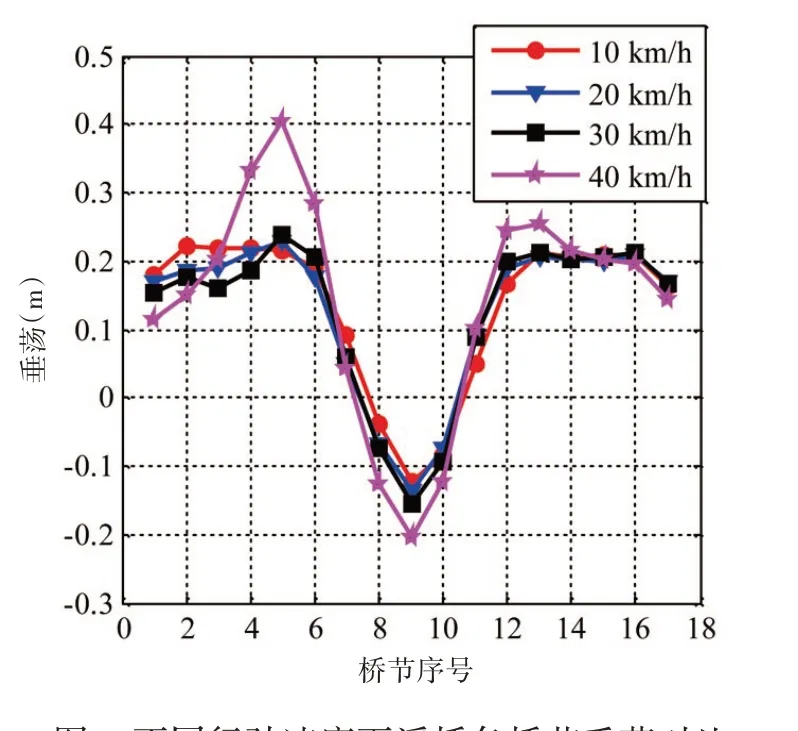
图8 不同行驶速度下浮桥各桥节垂荡对比Fig.8 Comparison of heave response of floating bridge pontoons under different vehicle speeds

图9 不同行驶速度下浮桥桥节系泊力时程曲线对比Fig.9 Comparison of mooring force time-history curves of floating bridge pontoons under different vehicle speeds

图10为不同行驶速度下浮桥各桥节系泊缆张力最大值的对比曲线，图中横坐标为桥节序号，纵坐标为系泊缆张力最大值。由图10 可知，各桥节系泊缆张力最大值均是随行驶速度增大而增大，而中间桥节P9 的系泊力最大值受行驶速度影响不太明显。此外，由图10可知，浮桥靠近两岸的系泊缆张力大于浮桥中段的系泊缆张力，这是由于车辆行驶到浮桥中段时承担车辆荷载的桥节增多，系泊缆受力更加均匀，因而系泊缆张力最大值变小。

3.2 波浪对浮桥动力特性的影响

为了研究波流联合作用下浮桥的动力特性，计算了在车辆行驶速度为20 km/h，波幅为0.1 m、0.3 m 和0.5 m，波浪周期为3.0 s，浪向为270°的规则波，和流速为1.5 m/s的水流联合作用下通载浮桥的运动响应及系泊力特性。图11为不同波幅下桥节P9重心处的垂向位移时程曲线，图中“0 m”表示流速为1.5 m/s 的水流与车辆荷载共同作用下的计算结果；“0.1 m”、“0.3 m”及“0.5 m”分别表示波幅为0.1 m、0.3 m和0.5 m 的规则波与流速为1.5 m/s的水流，以及车辆荷载联合作用下的计算结果。由图11可知，在仅有水流和车辆荷载作用下，桥节垂向位移仅在车辆通过该桥节或邻近桥节时产生较大幅值；而在波浪、水流及车辆荷载联合作用下，由于波浪的作用桥节会产生垂荡响应，在车辆通过桥节时由波浪和车辆荷载产生的垂荡响应将叠加起来，致使桥节垂荡谷值深度更大，这将导致桥节甲板更接近自由面，对通载造成不利影响。因此，需要特别注意波流环境中的通载安全和桥节上浪情况，尤其是在波幅大于0.3 m 后，60 t车辆通过桥节时甲板的上浪情况。此外，由图11可知，不同波幅作用下桥节的垂向位移幅值与波幅大小基本相同，这是由于周期为3.0 s的规则波波长约为14.0 m，大于桥节水线位置宽度的2倍，因此桥节呈现随波浪上下运动的现象。

图12（a）～（b）分别为不同波幅条件下桥节P9的横摇和纵摇时程曲线，图12的图例与图11的图例相同。由图12（a）可知，在纯水流作用下桥节的横摇幅值很小，主要是由于水流的作用导致桥节两侧系泊力不同，在通载时上游系泊缆张力进一步增大，从而引起通载时横摇幅值有所增大；而在波流联合作用下桥节出现了明显的横摇响应，并且在车辆通过桥节时由波浪和移动荷载引起的横摇响应存在叠加效应。而由图12（b）可知，桥节的纵摇响应主要由车辆荷载控制，波浪对纵摇的影响并不明显，这主要是由于浪向为横浪的缘故。

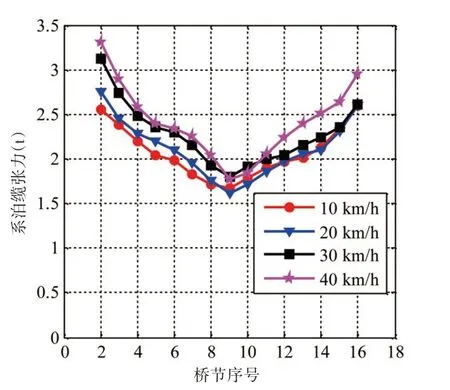
图10 不同行驶速度下浮桥各桥节系泊缆张力最大值对比Fig.10 Comparison of maximum values of mooring forces of floating bridge pontoons under different vehicle speeds

图11 不同波高下桥节P9垂荡时程曲线Fig.11 Heave response time-history curves of P9 under waves with different wave heights

图12 不同波高下桥节P9横摇和纵摇时程曲线Fig.12 Roll and pitch response time-history curves of P9 under waves with different wave heights

图13 为不同波幅下桥节P9 系泊缆张力时程曲线，图13 的图例与图11 的图例相同。由图13 可知，波浪、水流及车辆荷载联合作用下的系泊力明显大于仅有水流和车辆荷载作用下的系泊力，这是由于波浪导致桥节垂荡和横摇响应变大，系泊点位移量随之增大。与此同时，由图13可知，在波幅超过0.3 m后，系泊力将主要由波浪决定。

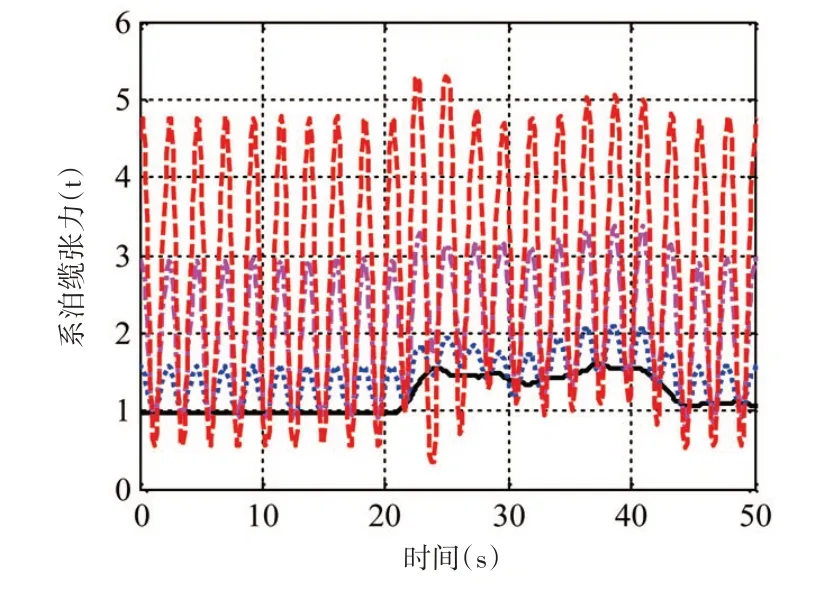
图13 不同波高下桥节P9系泊缆张力时程曲线Fig.13 Mooring force time-history curves of P9 under waves with different wave heights

4 结 论

本文采用势流理论及莫力森公式计算了浮桥受到的波浪力及水阻力，进而建立了波流环境中通载浮桥的运动方程，通过求解得到了考虑波浪和水流联合作用下，车辆通过时桥节的运动响应及系泊力时程曲线，在计算中同时考虑了桥节自由面变化的非线性影响。通过对计算结果的分析，得到以下主要结论：

（1）长浮桥在大吨位车辆通载时，各桥节的运动响应不尽相同，但所有桥节垂荡及纵摇响应均随车辆行驶速度增大而增大，桥节运动幅度增大的时长则随行驶速度增大而减小；此外，浮桥中后段桥节出现了不同程度的位移波堆积现象，该现象在车辆高速行驶时更为显著。各桥节系泊缆张力最大值均是随行驶速度增大而增大，而中段桥节系泊缆张力最大值小于两侧桥节系泊缆张力最大值。

（2）波浪引起的浮桥运动响应与车辆荷载引起的运动响应具有一定的叠加效应，特别是垂荡响应的叠加效应比较明显；系泊力也同样存在上述叠加现象，但在波幅变大后，系泊力将由波浪决定。