跟踪微分器改进算法的应用分析
2021-03-09李宏扬
李宏扬
(陆军装甲兵学院士官学校, 长春 130000)
0 引 言
在数学上很容易求取一个变量的导数或微分, 但对于实际的工程应用却不是一个简单问题, 由于工程实践中常常需要提取信号的微分形式, 因此这个问题一直困扰着控制领域的学者们。在工程控制领域, PID(Proportional Integral Derivative)控制算法是最受欢迎的控制方式之一[1], 其微分环节的实现通常采用超前网络等方法近似获取。此方法虽然改善了系统性能[2], 但会导致精确度下降, 同时还会引入噪声。针对这一问题, 韩京清[3]提出了跟踪微分器(TD: Tracking Differentiator)的概念, 为工程上提取微分信号提供了一种行之有效的方法, 即安排过渡过程的方法[4]。传统的TD取得了许多实际应用成果, 例如在光电稳定平台[5]、 桥式吊车[6]和卫星姿态控制[7]等方面都起到了非常好的控制效果, 同时也衍生出多种不同形式的跟踪微分器[8-9], 但算法还存在一些缺陷, 例如在系统进入稳态后, 传统的TD会产生高频振颤现象[10]; 此外当输入信号中混入噪声时, 传统TD很容易出现噪声放大效应。为解决传统跟踪微分器的缺陷, 笔者提出一个新的最速综合控制函数改进算法, 并引入到跟踪微分器中。
1 跟踪微分器新旧算法对比
跟踪微分器的功能结构图如图1所示。

图1 跟踪微分器结构图Fig.1 Structure diagram of tracking differentiator
其中v(t)是给定输入信号, 经过跟踪微分器TD后, 得到两个输出信号x1(t)和x2(t), 对给定输入信号v(t),x1(t)跟踪v(t),x2(t)是x1(t)的微分。由此可以看出, TD动态系统不仅能快速跟踪系统的给定输入信号, 还能提取出近似的微分信号。
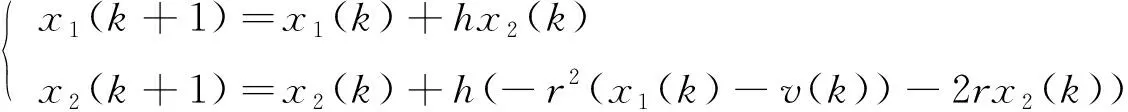
(1)
其中h是函数的积分步长,v(k)是TD的输入信号。于是可以得到二阶串联积分型系统

(2)
在式(2)中,f(·)是非线性函数, 将二阶积分串联型系统的原点作为终点, 即可求出快速最优控制的综合函数为

(3)
将式(3)代入式(2)中, 可得

(4)
将式(4)中的x1改为x1-v, 可得
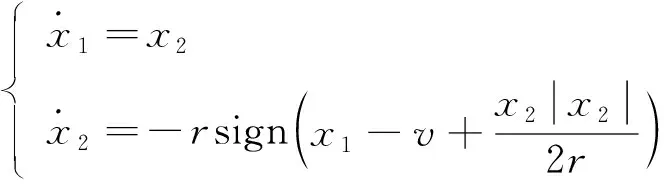
(5)
将式(5)所示的系统称为非线性跟踪微分器[12]。将式(5)进行离散化可得最速跟踪微分器
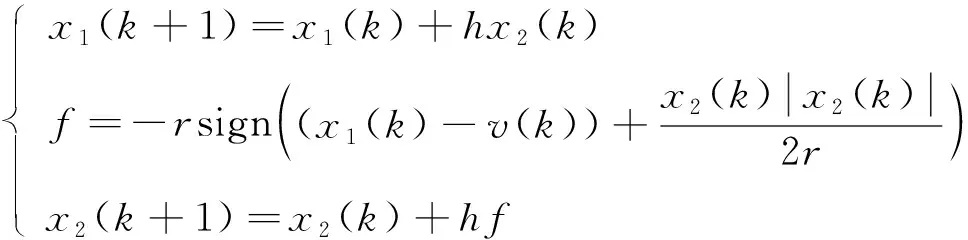
(6)
在系统进入稳态后, 利用式(6)的最速跟踪微分器会产生高频振颤现象, 于是又引入了一个新的最速综合控制函数fhan(x1,x2,r,h0), 其算法如下
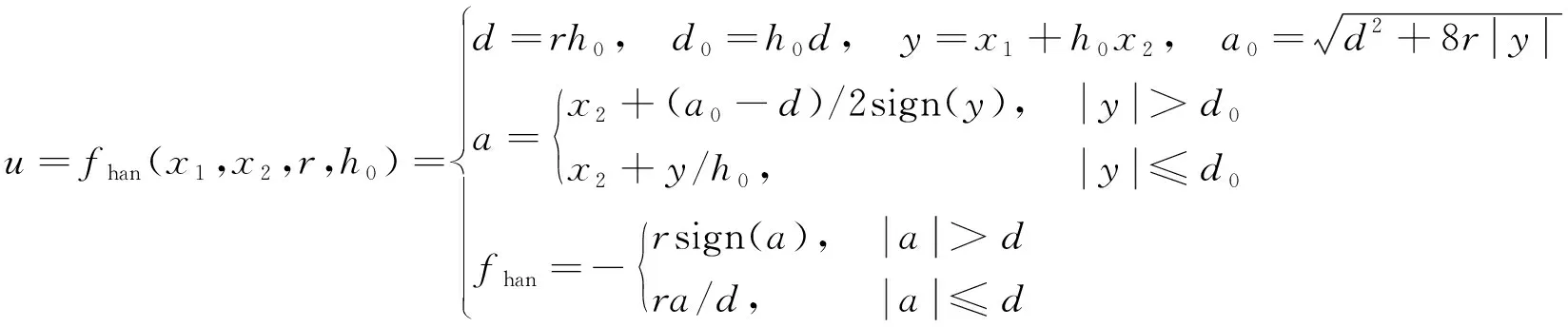
(7)
其中h0是TD的滤波因子, 起滤波作用。将式(7)代入式(6)中, 得

(8)
将其称为新的最速跟踪微分器, 即改进算法。TD对输入信号的跟踪快慢取决于r。
下面分别对采用式(6)和式(8)的跟踪微分器进行对比分析。速度因子r=16, 积分步长h=0.000 1, 新算法滤波因子h0=0.000 1。对图1所示结构的输入阶跃信号, 采用不同算法的微分输出信号如图2所示, 即图1中的x2(t), 其中图2b是图2a微分信号平稳状态时的局部放大图, 即6.5 s以后图像的局部放大图。由图2可以发现, 采用传统算法的跟踪微分器在进入稳态后出现高频振颤, 而采用改进算法的跟踪微分器则没有振颤, 这表明采用改进算法能克服传统微分器缺陷, 消除高频振颤。

a 对阶跃输入信号微分的跟踪 b 对阶跃输入信号微分的跟踪局部放大
2 采用改进算法TD的跟踪特性分析
对图1所示的结构图, 利用Matlab/Simulink分别进行阶跃和正弦信号输入仿真实验分析。实验条件如下: 积分步长h=0.000 1, 滤波因子h0=0.000 1, 速度因子r=20。阶跃输入条件下的跟踪性能如图3所示。在相同条件下, 通过图3发现采用改进算法的TD能比传统算法更快速地跟踪上阶跃输入, 但改进算法在输出微分信号时超调较大。正弦输入下的跟踪性能如图4所示。图4表明在相同条件下, 采用改进算法的TD能快速准确地跟踪上输入信号以及准确提取微分信号, 而采用传统算法的TD则已经发生了严重的畸变。

a 跟踪阶跃输入信号 b 跟踪阶跃输入信号的微分
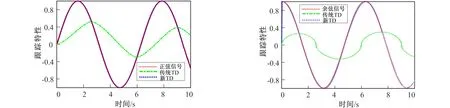
a 跟踪正弦输入信号 b 跟踪正弦输入信号的微分
不同r时阶跃输入下的跟踪性能如图5所示。在图5中, 随着速度因子r的增大, 响应时间越来越快, 提取微分信号时滞后越来越小。r不同时正弦输入下的跟踪性能如图6所示。在图6中, 随着速度因子r的增大, 跟踪正弦输入越来越快, 误差越来越小, 而且提取的微分信号滞后越来越小。通过图5和图6可以得到如下结论, 随着速度因子r的增大, 跟踪微分器对输入信号的跟踪又快又精确, 信号的提取滞后越来越小。

a 跟踪阶跃输入信号 b 跟踪阶跃输入信号的微分

a 跟踪正弦输入信号 b 跟踪正弦输入信号的微分
3 采用改进算法TD的滤波特性分析
由于改进算法中引入了滤波因子, 所以具有了滤波功能。对图1所示的结构图, 利用Matlab/Simulink进行仿真实验分析。实验条件如下: 积分步长h=0.000 1, 速度因子r=100, 在系统输入叠加功率为0.001的白噪声。不同滤波因子在叠加白噪声阶跃输入下的跟踪性能和不同滤波因子在叠加白噪声正弦输入下的跟踪性能如图7和图8所示。由图7和图8可以发现, 随着滤波因子的增加, 滤波作用增强, 但系统延迟时间增大, 因此, 在选择参数时要对滤波和滞后进行折中。

a 跟踪阶跃输入信号 b 跟踪阶跃输入信号的微分

a 跟踪正弦输入信号 b 跟踪正弦输入信号的微分
4 结 语
笔者对跟踪微分器的改进算法和传统算法数学离散过程进行了推导, 利用Matlab/Simulink软件中的S-函数对阶跃输入以及正弦输入条件进行了仿真实验分析。通过仿真对比传统与改进算法可知, 采用改进算法的跟踪微分器不但能快速跟踪系统的输入信号并能提取输入信号的微分信号, 同时消除了传统算法进入稳态后的高频振颤现象; 改进算法引入了滤波因子, 使跟踪微分器还能有效抑制噪声, 恢复原始信号, 所以滤波作用显著。传统PID控制的微分形式和积分形式都只对给定和反馈的误差信号进行处理, 而跟踪微分器却能提取信号的微分形式, 根据这一特性, 可以把跟踪微分器和PD(Proportional Derivative)控制器结合起来, 这将是下一步要深入研究的工作内容。
