船舶大气污染物时频特征分析
2021-03-09封学军沈金星
庄 凯,封学军,王 康,沈金星
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.河海大学土木与交通学院,江苏 南京 210098)
0 引言
随着长江南京段以下12.5 m 深水航道工程于2018年5月全线贯通,5 万吨级集装箱船可直达南京,有效改善了长江江苏段的通航条件,海进江运量增长迅速。 明确新的航行条件下航道内船舶大气污染物的排放情况,为航道环境治理提供支撑。
在船舶大气污染物测算方面,CORBCTT J J 等[1]于2000年提出排放测算的一个初步计算公式,以船舶的营运里程、货物量数据计算了美国所有的通航水域中的NOx和SOx排放量;2009年JALKANCN J P 等[2]引入了船舶自动识别系统中的船舶航行数据,应用船舶交通量排放模型对波罗的海的船舶排放进行了测算;2012年JALKANEN J P 等[3-4]继续在已有模型的基础上,增加了PM 和CO 的计算。 近年来,我国学者逐步引入船舶动力法,分别测算了环渤海地区、长三角地区、珠江流域等区域的船舶排放情况[5-10];在长江江苏段区域内,顾健等[11]应用本土化的船舶排放因子,对南京港龙潭港区2014年的船舶排放情况进行了测算;封学军等[12-13]应用了船舶动力法,在长江江苏段中选取典型断面,测算了长江江苏段2017年的船舶排放情况。
综合来看,上述研究主要着眼于以年、月为时间尺度的测算,鲜有对于特定区域进行单日、单时的排放测算,进而缺少对船舶大气污染物即时排放情况的说明,本文进行的船舶排放即时测算研究,可作为船舶大气污染物排放测算研究的补充。
船舶大气污染物的产生与多种因素有关,短周期因素:船舶的种类、船舶的负载情况、船舶的吨位、船舶的航行速度、区域内船舶航行的数量;长周期因素:航道水深条件、水流流速、航道的限行情况、通航贸易班轮航线、上下游港口基础设施配备、上下游港口主营货物种类、船舶航行燃油标准等。上述因素均会对区域内船舶的即时排放产生不同程度的影响,排放数据因此发生非线性、非平稳性的数据波动,污染物数据的波动难以直观的反映其排放特征与所受的影响因素,引入希尔伯特-黄变换对数据的波动进行分解,以期获取更多排放特征并对应分析。
希尔伯特-黄变换是一种常用的数据信号波动分析方法,应用于非线性信号处理。 SHI K 等[14]构建了NO2等污染物的非线性模型,结合希尔伯特-黄变换实现了对大气污染物的预测;杜娟等[15]采用集合经验模态分解方法与自组织临界理论确定了成都市冬季PM2.5的浓度时空变化规律。 FENG X 等[16]通过希尔伯特-黄变换对干散货港区的颗粒物质量浓度数据进行了时频特征分析,说明了区域内颗粒物质量浓度变化的主要影响因素。 对于区域污染物排放质量浓度数据的分析,希尔伯特-黄变换具有良好的适用性。
本文在应用船舶动力法对船舶大气污染物进行测算的基础上,将其分解为以30 s 为间隔的大气污染物排放数据,在单日、单时时间尺度上展现即时排放情况;将希尔伯特-黄变换引入船舶大气污染物排放数据的分析,获取排放数据在时域、频域的特征,明确其所受的影响因素,提出实现区域减排的建议。
1 研究区域与方法
1.1 研究区域
选取长江江苏段京杭运河与长江交界区域的一处断面,纬度范围:119.543°~119.553°,经度范围:32.215°~32.224°,其中东西向距离0.937 km,南北向距离1.938 km,覆盖全部江面,见图1。

图1 研究区域
研究区域的过境船舶包括: 长江口驶入的海船、航行于长江干线、京杭运河的内河船舶;船舶类别包括:普通货船、集装箱船、油船及其它船型。月过境船舶1.5 万艘,本文抽样船舶8 576 艘,抽样情况见图2。

图2 过境船舶抽样分布
过境船舶的情况反映深水航道工程投入运营之后,长江江苏段内船舶通航状况,内河船为主要过境船舶;船舶吨位主要为2 000 t 以下的小型船舶,累计频率大于60%,万吨级以上船舶通过数量极少。过境船舶的特征可反映长江江苏段过境船舶的复杂性、多样性,可作为长江江苏段的代表区域。
1.2 数据获取
原始数据来自:①船舶自动识别系统(Automatic Identification System,AIS),AIS 系统通过布设于航道沿线的数据基站可接收过往船舶的通航讯息,其中包括:船舶水上移动通信业务标识码(MMSI)、船舶瞬时时间(时间戳)、船首向、航迹向、船舶经度、船舶纬度;②中国船级社(China Classification Society,CCS),在CCS 数据库中,通过检索船舶的MMSI,可对应获取船舶的详细数据信息:船舶长度(m)、船舶宽度(m)、船舶吃水深度(m)、船舶总吨位(t)、船舶类型。
本文获取2019 全年研究区域的AIS 数据,提取每月第15日,共12 d 的数据作为样本数据,以30 s为间隔,对样本数据进行分解,单日获取2 880 组数据。 每组数据中包含30 s 内海船数量、海船平均船长、海船平均吨位、海船平均功率、海船平均航速、内河航船数量、内河航船平均船长、内河航船平均吨位、内河航船平均功率、内河航船平均航速。
1.3 船舶动力法
单艘船舶在航行的过程中,产生的主要大气污染物包括SO2,NOx,PM2.5,CO,VOCs,其中船舶的油品质量显著影响了SO2,PM2.5,VOCs 的排放;船舶发动机的功率、燃烧效率、工作时间等影响了NOx,CO的排放,计算公式如下:
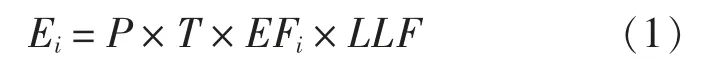
式中:i为污染物种类;Ei为对应某种大气污染物的排放量,g;P 为船舶主机或副机的发动机额定功率,kW;T 为船舶主机工作时间,h;EFi为对应某种大气污染物的排放因子,见表1[9-11],g/(kW·h);LLF(Low Load Factor)为船舶主机低负载调整系数,无量纲。当船舶以低速航行时,船舶主机对油品进行不完全燃烧,致使产生的大气污染物增多,一般认为当船舶主机负荷低于20%时,需对其排放因子进行进一步调整,船舶主机低负载调整系数示例见表2[17]。
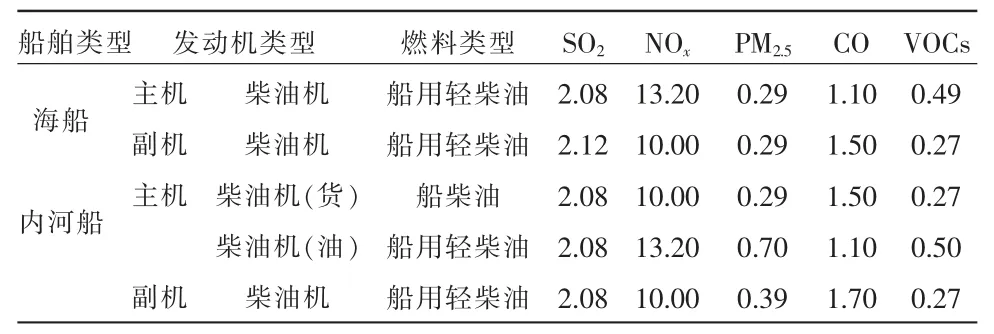
表1 船舶大气污染物排放因子 g·(kW·h)-1

表2 船舶主机低负载调整系数示例
1.4 希尔伯特-黄(HHT)变换
希尔伯特-黄变换分为经验模态分解(Empirical Mode Decomposition,EMD)和在EMD 分解基础上进行的希尔伯特变换(Hilbert Transform,HT)。
EMD 分解是将提取到的原始数据信号通过自适应的方式分解为若干多个本征模态函数(Intrinsic Mode Function,IMF),使得每个IMF 函数满足:①在整个时域区间内,IMF 函数的波动曲线过零点与曲线极值点的数量相等或最多相差1 个;②曲线上任何1 点的局部最大值与最小值的包络(包络线)均值必须为0。 经过EMD 分解之后,污染物浓度数据信号可以分解为若干个IMF 函数与余波之和,分解公式如下:
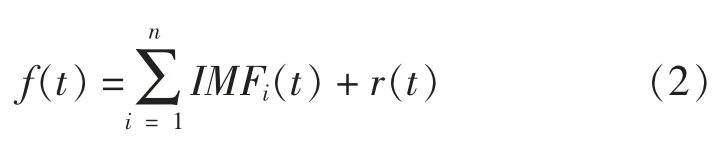
式中:f(t)为原始数据信号,mg/m2;IMFi(t)为第i 个IMF 函数,mg/m2;r(t)为原始信号数据中分离n 个IMF函数之后的余波信号,mg/m2。
将EMD 分解得到的IMF 函数进行HT 变换,变换公式如下:

通过HT 变换将一维实数信号转变为二维复平面上的解析信号,转变公式如下:

其中:
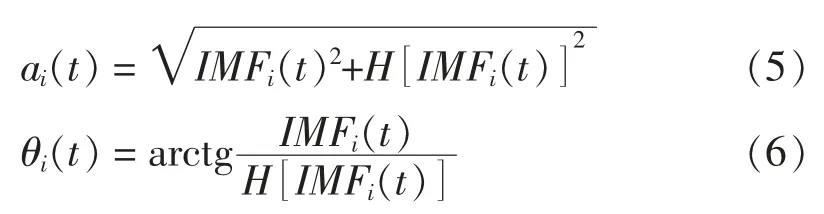
式(4)~式(6)中:Zi(t)为二维复平面上的解析信号;ai(t)为解析信号的幅度;θi(t)为解析信号的相位;j为Zi(t)的虚元素。
通过式(4)中的极坐标表达式,IMFi(t)的瞬时频率ωi(t)可以表示为式(7)。

ωi(t)反映了IMFi(t)的瞬时频率的波动情况,Hz。HHT 变换可以从原始数据信号中提取出频率波段相近的成分,形成不同的分量信号,并展现其频率随时间的变化。 将原始质量浓度信号在时间序列上的波动数据转化为频率波动数据,由此进一步表征一定时间尺度上大气污染物浓度数据信号的变化情况,获取研究区域内船舶污染物质量浓度的变化特征。
2 实证分析
2.1 即时船舶污染分布
研究区域内2019年对应的12 d 污染物平面浓度数据信号即时分布见图3。 由图3 可知,每日污染物平面浓度呈周期性分布,在每日日中时刻(10:00~15:00),污染物平面浓度达到峰值,SO2波动区间集中于0 ~0.10 mg/m2,NOx集中于0 ~6.19 mg/m2,PM2.5集中于0 ~0.25 mg/m2,CO 集中于0 ~0.74 mg/m2,VOCs 集中于0 ~0.98 mg/m2;以SO2排放为例,1月至9月日均排放量(对应1 ~9 d)为16.68 mg/m2,10月排放较其它月份显著上升,达到112.48 mg/m2,次月则出现明显跌落,下降至6.11 mg/m2,12月恢复至正常排放水平23.02 mg/m2。
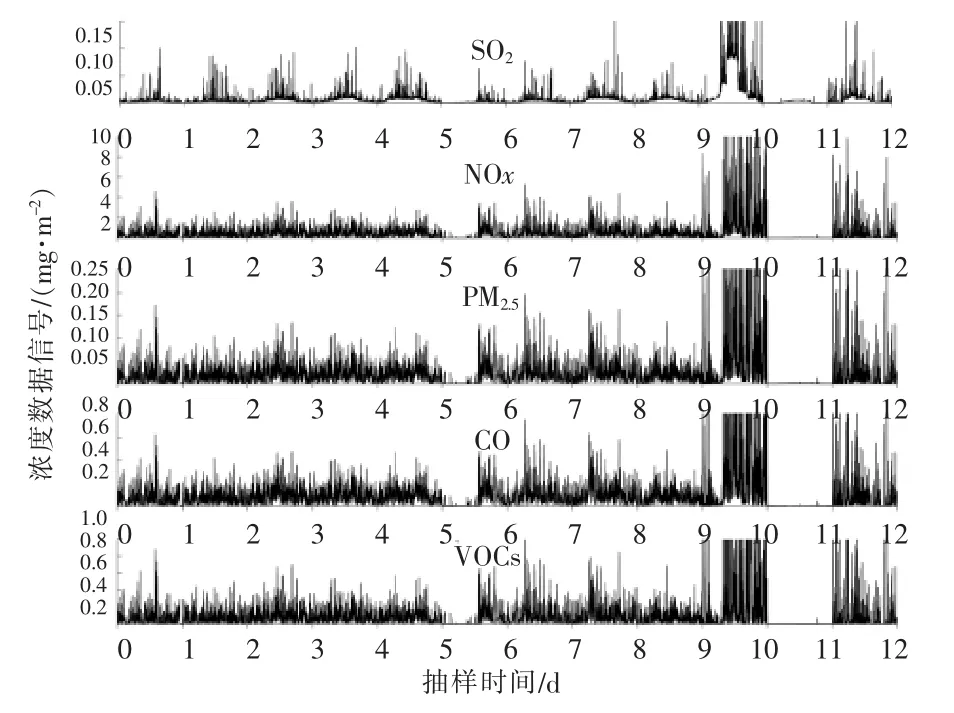
图3 大气污染物平面浓度数据信号即时分布
研究区域内24 h 全时段污染物平均总量见图4。 由图4 可知,各类大气污染物总量随时间的波动趋势基本一致。 每日06:00 起,单位小时内污染物总量开始逐步上升,18:00 后趋于平稳,缓慢下降。大气污染物整体排放趋势符合船舶航行的基本规律:在白天视线较好时较高,在日落后视线较差时较低,计算结果符合实际情况。NOx时均排放量最高,其后依次为VOCs,CO,PM2.5,SO2。

图4 全时段大气污染物平均总量
2.2 HHT 变换
将样本数据中的NOx平面浓度数据(12 d 平均信号)作为示例数据展示,进行EMD 分解,分解结果见图5,将分解得到的IMF 函数分量记为IMFi,NOx浓度波动可以分解得到9 个分量和1 个余量,即i=[1,9]。

图5 EMD 分解
对经过EMD 分解后的数据进行HHT 转换,在HHT 分布中,数据信号对应的频率具有明显的离散特性,各类污染物浓度数据频率波动范围见表3。 由表3 可知,航道内船舶大气污染物平面浓度数据信号的波动均为低频长周期波动,除SO2以外的其它种类污染物的波动频率范围一致。

表3 污染物平面浓度数据频率波动范围 Hz
2.3 边际谱分析
边际谱作为数据信号的频率特性之一,适用于通过各频段上的幅值分布,表征各频段数据信号对于原始数据信号的影响程度(mg/m2),计算公式如下:
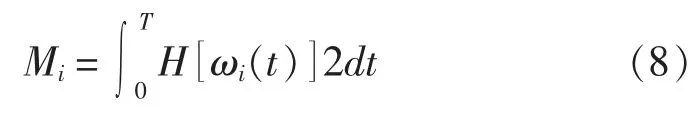
求得边际谱见图6。 由图6 可知,各类污染物数据信号的影响频段集中于低频段,其中SO2,PM2.5,CO,VOCs 的影响频段为0 ~0.007 Hz,NOx的影响频段为0 ~0.173 Hz,NOx的边际谱相较于其它种类污染物分布分散于更多频段。 低频长周期因素为数据信号波动的主要影响因素,对于未来的船舶大气污染物减排控制,需关注长周期因素的影响。

图6 船舶大气污染物平面浓度边际谱
3 结论与展望
3.1 结论
本文在基于HHT 的船舶大气污染时频分析的基础上,得到以下结论。
(1)研究区域内每日污染物平面浓度数据信号呈现周期性分布,每日日中时刻(10:00 ~15:00),污染物浓度达到峰值,SO2波动区间集中于0 ~0.10 mg/m2,NOx集中于0 ~6.19 mg/m2,PM2.5集中于0 ~0.25 mg/m2,CO 集中于0 ~0.74 mg/m2,VOCs 集中于0 ~0.98 mg/m2;10月排放较其它月份显著增加,各类污染物浓度数值均处于最高,次月则出现明显跌落,12月恢复正常排放水平。
(2)各类大气污染物总量随时间的波动趋势基本一致。 每日06:00 起,单位小时内污染物总量开始逐步上升,18:00 后趋于平稳缓慢下降;NOx时均排放量最高,其后依次为VOCs,CO,PM2.5,SO2。
(3)所有种类污染物浓度数据信号对应的频率具有一定的离散特性,研究区域内船舶大气污染物平面浓度数据的波动均为低频长周期波动。
(4)影响污染物平面浓度数据波动的主要为长周期因素,对于未来的船舶大气污染物减排控制,需关注长周期因素的影响。
3.2 展望
本文在应用船舶动力法的基础上,对研究区域内船舶大气污染物排放进行测算,实现单日、单时尺度上船舶大气污染物排放情况的即时展示,测算结果符合一般规律;在测算的基础上引入HHT 分析,将研究区域中的污染物平面浓度数据信号转化为频域信号,明确其频域特征。 需要注意的是,HHT 分析仅能从污染物数据信号本身出发,对数据的信号进行分解,在频率的角度对可能的影响因素进行分析,无法实现对于分解信号与实际因素的对应。 因此在区域船舶大气污染物的排放分析研究中,需进一步明确实际因素对应的影响效果。
