基于EMD-BiLSTM的太平洋大眼金枪鱼渔场预报模型研究
2021-03-09袁红春张天蛟
袁红春,张 永,张天蛟
(上海海洋大学信息学院 上海 201306)
金枪鱼是一种具有定期洄游行为的鱼类,因其资源量丰富,经济效益显著,已经成为世界各沿海国家的重点捕捞鱼种[1-2],更是中国远洋渔业的主要产业之一[3]。大眼金枪鱼(Thunnusobesus)属于金枪鱼的一个重要分支,是大洋性金枪鱼渔业的主捕鱼种之一[4-6]。研究表明,其分布受表层水温、次表层水温、叶绿素等众多环境因子的影响[7]。在世界金枪鱼的捕捞总产量中,大眼金枪鱼产量近几年一直稳居第3位[8]。大眼金枪鱼在各海域分布广泛[9],南太平洋属于重要产区[10-11]。因此,构建高精度的渔场预报新模型,提高渔场预报水平,将对中国大眼金枪鱼的捕捞与研究工作产生积极作用。
近年来,对于中心渔场预报模型及方法,众多学者进行了大量的研究。Aoki 等[12]用3个隐层的 BP模型,在日本远东海域针对拟沙丁鱼渔获量进行相关预报研究,得出神经网络可作该领域分析和预测工具,并适用于鱼类非线性多变量的问题。但环境因子选用SST和浮游动物密度,种类偏少,且模型层数较多,对训练及预测速度会产生一定的影响。周为锋等[13]采用贝叶斯概率的方法对金枪鱼进行渔场预报,取得了一定效果,可以为金枪鱼的生产提供参考,但所用环境因子为SST,过于单一,且绝对误差为0.349,仍有降低空间。李娜等[14]使用BP网络在大西洋相关海域进行阿根廷柔鱼的渔场预报,将月份、经纬度、海面高度、海面温度当作模型的输入因子,试验过程中选择不同结构的BP网络作对比。但所涉模型均为BP相关模型,未能说明BP模型较其他模型的优越性。陈雪忠等[15]利用随机森林模型,在印度洋海域对长鳍金枪鱼渔场分布及变动进行预报。但所涉环境因子均为海洋表层信息,且随机森林模型并不能很好地应对CPUE原始序列本身存在的波动性与无规律性对模型预报产生的不良影响。
上述渔场预报模型研究存在以下不足:预报模型结构比较普通,性能一般;所选环境因子类型不足,没有更全面地呈现生存环境;与其他预报模型性能对比不够充分,且多数模型结合环境因子直接利用CPUE序列进行训练与预报,均受CPUE原始序列的波动性与无规律性影响较大,预报难度较高且误差偏大。若能构造一个渔场预报模型,将海洋表层与海洋面以下环境因子结合渔业数据进行模型训练与预报,并将所受原始序列特征对预报模型的不良影响降到最低,则有望获取抗干扰能力更强、预报误差更小的预报效果。基于此,在深入研究神经网络理论的基础上,提出一种基于经验模态分解机制和双向长短时记忆神经网络(EMD-BiLSTM)的渔场预报模型,结合海洋表层和海平面以下环境因子辅助模型训练与预报,并对比分析随机森林、BP、LSTM、Bi-LSTM等模型的预报效果,以期实现更科学实用的渔场预报新模型。
1 材料与方法
1.1 试验材料
1.1.1 数据来源
所用渔业数据来源于深圳市联成远洋渔业有限公司的太平洋延绳钓捕捞数据。为保证试验数据的统一性,一律采用该公司2014年1月至2018年12月的太平洋海域大眼金枪鱼渔业数据,时间分辨率为月,空间分辨率为1°× 1°,选取数据的作业海域为2°S~14°N,157°E~175°E,具体类别有年、月、经度、纬度、钓钩数、大眼金枪鱼渔获量(尾)。单位捕捞努力渔获量(CPUE)为试验的预测参数[16],其计算过程如公式(1)所示:
XCPUE=A/H
(1)
式中:XCPUE—单位捕捞努力量,尾/千钩(ind/khooks);A—渔获量,尾(ind);H—钓钩数,千钩(khooks)。
另选取2014年1月至2018年12月与渔业数据相对应的环境数据,包括月、经度、纬度、海表面温度SST、海表面盐度SSS、叶绿素a质量浓度,同时综合考虑到大眼金枪鱼习惯性栖息水深[17-18],初步在水深500 m范围内选取15个深度值处的海水温度与海水盐度,其中各深度值如下:0、5、10、20、30、50、75、100、125、150、200、250、300、400和500 m,然后对该15个数据进行相关性分析,继而选用相关性较大的环境因子作为模型的输入。其中的海水温度(SST~T500 m)与海水盐度(SSS~S500 m)数据均来源于亚太数据研究中心(APDRC)的Argo数据库,而叶绿素 a 质量浓度数据取自于美国国家海洋和大气管理局(NOAA) 环境数据库。
1.1.2 相关性分析
将处理好的环境数据与渔业数据相匹配,得到符合模型要求的数据集,使用SPSS软件对该试验数据进行双变量相关性分析,找出时空因子、环境因子与CPUE值之间的关系,以及相关性大小。其中双变量线性相关程度计算公式(2)如下:
(2)
式中:r12— 1、2两变量相关系数大小;s12— 1、2两变量协方差大小;s11—变量1的方差;s22—变量2的方差。
在分析结果中,若0.01 表1 双变量相关分析 分析发现,所列举影响因子中,叶绿素a质量浓度、温度和盐度与该区域CPUE值均有较大相关性。且对于温度、盐度,与CPUE值相关性较大的在100~300 m深度范围。因此,本研究选用叶绿素a质量浓度和海表面以及水深100 m、200 m、300 m处的温度值、盐度值作为试验数据,得到数据集A。 将月、经纬度、温度、叶绿素a质量浓度、盐度用作训练参数,各月对应CPUE值作为预测参数,对试验数据集A截取80%作为训练集,10%作为验证集,10%作为测试集,用于预报模型试验,得出各预报模型的预报误差并进行误差大小对比。 1.1.3 数据归一化 数据各因子量级有所区别,将会对模型产生不良影响,为保证试验结果的准确性,此处目标变量和影响因子均经过公式(3)归一化到[0.1,1]区间中[20-21]。 (3) 式中:xn—某一影响因子第n条数据;xmax—此影响因子中最大值;xmin—此影响因子中最小值。 1.2.1 EMD基本原理 经验模态分解机制(EMD)是一种新方法,用于信号处理,主要针对非线性、非平稳性时间序列[22]。数据自身特征尺度存在区别,该机制根据特征尺度提取数据的本征模态函数IMF,使其逐渐平稳化[23]。一个显著特征是消除了基函数无自适应性问题,无须进行预处理便可将陌生信号分解。假设数据序列为s(t),具体步骤如下[24]: 1)通过计算机编程,于原始序列中得到极值; 2)以局部的下部极小值和上部最大值为插值点,实施3次样条插值,得到所需上下包络线; 3)计算两条包络线,求出均值f1; 4)计算k1=s(t)-f1,若k1是本征模态函数要求,则k1属于s(t)的第一阶分量,否则实施步骤5); 5)把k1视作新序列,再一次进行上面1~4步骤,直至求出s(t)的第一阶分量; 6)获得第一阶分量之后,所剩数据为: c1=s(t)-IMF(1) (4) 7)将数据c1重复视作原始序列,实施步骤1~6,依次求出IMF(2),…,IMF(n)以及残余分量r(t),则有: (5) 将上述分解过程绘制为流程图(图1)。 1.2.2 LSTM与Bi-LSTM模型介绍 LSTM网络模型于1997年提出,相对于RNN网络,LSTM在其神经元内添加三类全新门结构[25]:输入门,输出门以及遗忘门,为梯度消失问题提供一个有效的处理办法。其模型结构见图2。 上述门结构在时刻t时运算公式如下: ft=σ[Wf(ht-1,xt)+bf] (6) it=σ[Wi(ht-1,xt)+bi] (7) (8) ot=σ[Wo(ht-1,xt)+bo] (9) (10) ht=ottanh(ct) (11) LSTM网络被广泛使用且性能良好,基于此,Graves等[26]又提出双向长短时记忆神经网络(Bi-LSTM),该网络由LSTM改进后产生,将两个LSTM网络置于前后方向共同训练,与同一输出层连接,捕捉过去和将来的信息[27]。Bi-LSTM的基本结构见图3,其中,Xi为网络输入,Yi为特征向量通过该网络后的输出结果。 精确性和稳定性是两个重要的模型评价指标。依据相关文献[28],利用XMAE、XRMSE对所用模型进行统计对比分析,计算公式如下: (12) (13) 式中:n—测试集个数;Ct—CPUE的预测值;Rt—CPUE的真实值;XMAE—绝对误差,其值越小则代表预报越准确;XRMSE—均方根误差,其值越小则代表预报模型越稳定。 试验环境为基于Python3.6的TensorFlow1.3框架,操作系统为Windows10,GPU为NVIDIA GTX 1060,通过CUDA9.0进行加速运算,CPU为Intel i5-3470K。 建立了基于EMD-BiLSTM的渔场预报新模型,并在该深度学习平台上进行基于随机森林、BP、LSTM、Bi-LSTM、EMD-BiLSTM的渔场预报试验。根据各模型在同一试验数据集下的试验效果进行优越性综合评定,继而验证EMD-BiLSTM模型的有效性。基于EMD-BiLSTM的渔场预报模型在该研究中的试验步骤为: 1)通过对大眼金枪鱼CPUE序列进行EMD分解,获得所需IMF分量和残余项; 2)将IMF分量与影响因子共同处理,实现数据归一化,并转为监督学习问题,以满足Bi-LSTM的要求; 3)结合影响因子自动为IMF分量分别建立Bi-LSTM模型,进行训练与预报; 4)所有预报均产生对应结果,将所有预报结果序列重构,再反归一化操作,获得最终预报值。 将试验过程绘制为流程图(图4)。 2.3.1 EMD分解结果 取5°N~9°N,156°E~161°E海域的2018年7月~12月数据使用EMD机制实施分解作为该处结果展示,CPUE序列作为EMD的输入,输出为该值各分解分量和一个残余分量。由图4可以看出,EMD分解首先从信号中分解出高频分量,再逐步得出低频分量,最后获得一个变化缓慢的趋势信号Res。结果表明,大眼金枪鱼CPUE序列经过EMD机制分解,共得7个IMF分解分量与一个残余项Res。图4中,分量IMF1~IMF3具有较高的频率和较大的突变性,而且具有一定的随机性与无序性;分量IMF4~IMF7整体的变化比较平稳,而且变化的规律相比IMF1~IMF3较强,残余项Res则代表该CPUE序列整体变化趋势。 分解过程有效降低了原始序列的波动性与无规律性对预报结果的影响,使原本复杂的序列得到简化,最终使得基于Bi-LSTM神经网络模型的预报过程得到简化,预报误差进一步降低。分解结果如图5所示。 2.3.2 预报误差结果 表2是预报误差统计结果。由表2可知,EMD-BiLSTM模型预报精度最高,MAE、RMSE分别是0.033和0.056。相比于随机森林模型,MAE和RMSE分别降低0.284、0.476;相比于BP模型分别降低0.048、0.208;相比于LSTM模型分别降低0.035、0.096;相比于Bi-LSTM模型分别降低0.018、0.053。 综合来看,基于EMD-BiLSTM的大眼金枪鱼渔场预报模型比其他模型预报精度更高,预报效果比文献中涉及的BP模型和随机森林模型更好,能对大眼金枪鱼CPUE值的变化规律与趋势实施更准确的预报。 表2 预报误差统计结果 2.3.3 损失值结果 数据集在LSTM、BP、Bi-LSTM、EMD-BiLSTM预报模型上的训练集与验证集损失值如图6所示。图中,纵轴代表损失值,横轴代表模型迭代次数,实线和虚线分别代表训练集损失值和验证集损失值。 从图6可以看出,在结合EMD机制之后,虽然模型复杂度有所提高,但可在一定程度上提高模型收敛速度,并降低抖动性。该模型将原始数据经过经验模态分解,然后跳过原始CPUE序列自动为各分量分别进行Bi-LSTM神经网络的预报,并将各预报结果进行序列重构,使Bi-LSTM神经网络的数据处理优势得以充分发挥,模型性能更为理想。 2.3.4 CPUE值预报结果 为降低可视化图形的曲线拥挤度,提高视觉清晰性,取5°N~9°N,156°E~161°E海域的2018年7月~12月数据进行预报与展示,生成CPUE值的可视化预报结果图。LSTM、BP和Bi-LSTM模型与EMD-BiLSTM模型的预报结果分别如图7所示。通过对比图中两曲线,直观上看,LSTM与BP模型的预报结果不太理想,预报值曲线与实际值曲线之间的拟合度较低,存在一定程度的误差;Bi-LSTM模型的预报效果有所提高,但两曲线间仍偏差较大;而在结合了经验模态分解机制之后,EMD-BiLSTM模型下的两曲线较为接近,预报值与实际值相对吻合。可见,基于EMD-BiLSTM模型的预报准确度更高,预报结果与实际CPUE值基本一致。因此,将经验模态分解机制与Bi-LSTM相结合可以显著提高模型的预报效果。 许多学者对于中心渔场预报模型及预报方法进行了大量研究,所用模型包括传统预报模型与神经网络模型,如随机森林模型[15],其通过使用若干预测器来获取更多信息,进而减少拟合数值和估计分割的偏差,而且可对高维度数据进行处理,但性能一般,经试验,在结合多种环境因子对CPUE进行相关预报时,预报误差偏大。对于BP网络[14],往往通过增加隐含层数并反复调整神经元之间权值达到预报目的,但其结构选择缺乏统一的理论指导,只能凭借经验,且不含有记忆单元,不能有效保留隐含层权重与目标因子的拟合度。而LSTM神经网络[29],增加了输入门、输出门和遗忘门,新增的记忆单元能够更好地适应数据的变化,从而为梯度消失问题提供一个有效处理办法,预报误差相对减小,但相比于Bi-LSTM神经网络,其对过去、将来信息进行有效整合的能力有所欠缺,因而存在较大预报误差。 本研究将EMD机制和双向长短时记忆网络进行有效结合,探索并构建的EMD-BiLSTM渔场预报新模型,引入了一种信号处理新方法即经验模态分解机制(EMD),该机制依据数据不同特征尺度,提取本征模态函数IMF,从原始信号中分解得出高频分量,再逐步得出低频分量,最后获得一个变化缓慢的趋势信号Res,使各分量波动性比原始CPUE信号有所降低,平稳性有所提高。该模型在对原始序列做EMD分解、获取IMF分量之后,会跳过原始CPUE序列直接为平稳性较好的各分解分量分别进行Bi-LSTM预报,在简化了预报难度的同时,又提供了多个Bi-LSTM神经网络,使得记忆功能较强的该网络进一步发挥出数据处理优势,最后对各序列进行重构并获得最终预报结果。 结果显示,在CPUE值的预报可视化图形中,结合了EMD机制之后的新模型,相比于其他所涉及对比模型,图中两曲线更为接近,预报值与实际值相对吻合,可见新模型预报效果更好。同时,依据相关文献[28],该试验也采用了绝对误差XMAE和均方根误差XRMSE两种评判方式进行结果对比与评价。其中,绝对误差越小则代表预报越准确,均方根误差越小则代表预报模型越稳定。根据试验结果,在所用模型中,EMD-BiLSTM模型预报误差最小,其中MAE、RMSE分别是0.033和0.056,相比于随机森林模型分别降低0.284、0.476,相比于LSTM模型分别降低0.035、0.096,而相比于BP模型分别降低0.048、0.208,相比于Bi-LSTM模型也分别降低了0.018、0.053。可见新模型在准确性和稳定性方面预报性能更好,并且具有很好的适用性。另外,该模型中各路Bi-LSTM其含有的记忆功能又能有效保留隐含层权重与目标因子的拟合度,使模型的整体预报效果得到极大提升。 在试验中运用EMD机制可减少CPUE原始序列本身特征造成的影响。为更全面模拟环境提升预报效果,该试验利用海洋表层和海平面以下的环境数据,共同辅助模型训练与预报,做到水面水下数据有效结合,从立体层面协助新模型做大眼金枪鱼的预报研究,提升了预报结果。经过相关性分析,在该海域所列环境因子中,叶绿素a质量浓度和温度均与CPUE值具有较大相关性。这是因为,金枪鱼的分布主要受海洋环境和饵料生物影响,海洋环境主要包括水温、温跃层和溶氧等[31-32]。其中,饵料生物也会随着栖息环境的改变游至适宜的栖息位置,进一步影响大眼金枪鱼的分布。大眼金枪鱼的具体栖息水深目前尚无统一定论,有相关研究表明,对CPUE影响密切的深度值在250 m[32],但日本学者调查的结果表明,大西洋大眼金枪鱼延绳钓CPUE最高值在300 m水层以下[33];也有研究表明,在大西洋,超过300 m水层的深水延绳钓 (400 m),大眼金枪鱼CPUE依然很高[34]。将来可考虑针对大眼金枪鱼适宜栖息深度做深入研究。由于大眼金枪鱼是洄游性海洋鱼类,影响其渔场分布的因素可能不止这些,比如风向风速、溶氧量、海流等环境因子[30]。接下来将搜集更多的影响因子投入试验进行综合分析,希望能进一步提升试验效果。 构建了基于EMD-BiLSTM的大眼金枪鱼渔场预报新模型,与传统方法相比,该模型可有效降低CPUE原始序列的波动性与无规律性对预报的不良影响,简化原始序列,继而简化了Bi-LSTM对大眼金枪鱼CPUE的预报复杂性,减小预报误差。这在一定程度上弥补了传统模型的不足,为大眼金枪鱼渔场预报工作提供了一种新思路。后期仍考虑整理更多的海洋环境因子,并对模型本身做进一步完善,提高模型在渔场预报方面的效果。另外,该研究主要是根据CPUE与环境因子这类空间特征数据进行分析,对时间关联性方面考量不足,因此,后期准备将每一年中各季度下的渔场CPUE添加到影响因子中,结合时间、空间,共同完成模型的训练与预报工作。同时,CPUE作为捕捞效率的一个结果,其高低除与渔场环境参数有关外,还与渔捞水平与能力可能也有一定关系,下一步将针对该点努力获取多方面数据投入到模型试验与研究工作,进一步完善模型的预报性能。 □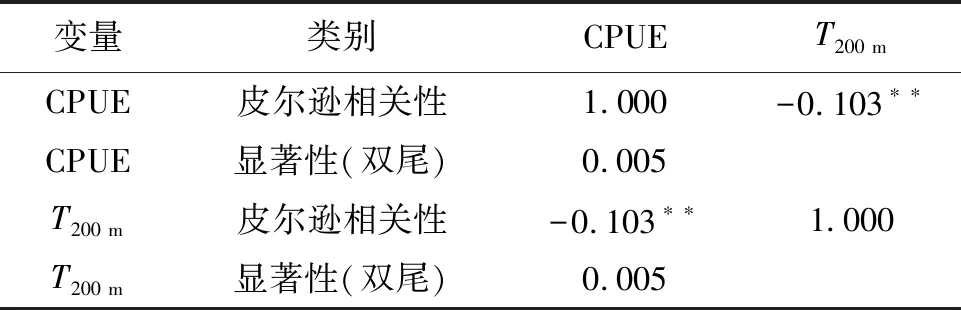
1.2 方法原理

1.3 试验误差分析方法
2 试验及结果分析
2.1 试验平台
2.2 试验过程
2.3 结果

3 讨论
3.1 与其他预报模型的比较
3.2 其他影响因素
4 结论
