基于分数阶导数的金属橡胶动态特性建模

余慧杰，贺 涛

(上海理工大学机械工程学院，上海 200093)

1 前 言

金属橡胶是一种新型结构阻尼材料，可经特殊的工艺将一定质量的、拉伸开的、螺旋状态的金属丝有序地排放在冲压或碾压模具中，然后用冷冲压的方法压制成形，再经必要的热处理制备而得[1]。近年来，金属橡胶作为新型的减振材料得到了越来越多的重视，国内外众多学者对金属橡胶材料及其静动态特性做了大量研究[2-6]。金属橡胶具有变刚度、变阻尼的非线性迟滞特性，是一种典型的黏弹性材料，但由于其本构关系非常复杂，难以用常规的模型描述其动力学特性。

分数阶微积分是整数阶微积分向非整数阶微积分的拓展研究，其诞生最早可追溯到Newton和Leibniz创立微积分的时代。然而长期以来，由于缺乏物理和力学等背景学科的支持，分数阶微积分一直作为纯理论而被数学家所研究。直到20世纪80年代研究人员发现分形几何、记忆过程等现象及过程可以与分数阶微积分建立起密切的联系[7]。现有的黏弹性标准流变学模型如Maxwell模型、Kelvin-Voigt模型、经典三元固体模型等都不能够准确地描述黏弹性材料复杂的力学行为[8]。但是，将这些经典模型中的整数阶导数扩展到分数阶，能够有效弥补这些模型的不足。

本研究在经典三元固体模型的基础上，用Abel体代替Newton粘壶，得到分数阶三元动力学模型；建立了三次非线性弹性力模型和黏弹性力模型。同时对金属橡胶材料进行动态试验，结合试验结果与所建立的模型，进行参数识别与模型验证；通过试验结果和数值结果的对比，分析了经典三元模型和分数阶三元模型描述金属橡胶材料动力学性能的准确性。结果表明，采用分数阶三元模型，可以在较少参数的情况下更好地描述金属橡胶不同工况下的动态特性，为金属橡胶材料更好地在实际工程中的广泛应用提供参考。

2 实 验

2.1 试验过程

金属橡胶材料动态试验所用试件如图1所示，金属丝材料为奥氏体不锈钢1Cr18Ni9Ti，密度为ρs=7.85×10-3g/mm3，螺旋卷直径为0.8 mm，相对密度(金属橡胶构件密度与金属丝材料密度之比)为0.1，外形尺寸(外径-内径-高度)为φ10 mm-φ5 mm-8.5 mm。试验采用ElectroForce3330多功能试验机，装置如图2所示。该试验机的动态力范围为-3000～+3000 N，位移范围为0～25 mm，频率范围为0～100 Hz。试验机配套了Win test测试软件，该数据采集分析软件可设定设备响应参数和加载参数，可对测量数据进行实时采集；装置测试系统配有DMA材料动态特性机械性能分析软件，可以进行载荷加载并分析计算出动刚度、损耗因子、存储模量(动刚度实部)、损耗模量(动刚度虚部)等参数大小，并分析其变化规律。

图1 金属橡胶试件Fig.1 Metal rubber specimens

图2 动态特性实验装置Fig.2 Dynamic test device

由于本试验的金属橡胶试件对位置精度比较敏感，故要求所设计的夹具能够精确地安装定位。在夹具中，双头螺栓可以很方便地调整回形刚圈的位置，使其处于上下金属橡胶中间位置，避免上下金属橡胶受力不均；调节螺杆和锁紧垫片可以很方便地调整金属橡胶的预压缩量，有效减少夹具拆卸次数，提高试验效率。所设计的夹具结构简单、试件定位准确、安装便捷牢靠。

在试验中，选用相同预压量、丝径和尺寸的金属橡胶试件10组，分别进行动态拉压试验。加载频率10 Hz，振幅±1.5 mm，可以得到如图3所示的载荷-位移迟滞回线。

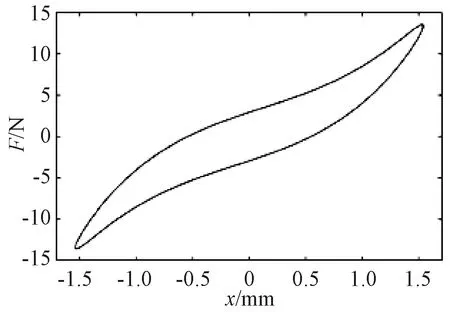
图3 金属橡胶迟滞恢复力曲线Fig.3 Force-displacement curve of metal rubber

2.2 试验结果

通过Dynamic Mechanical Analysis(DMA)动态分析软件得到其存储模量和损耗模量变化曲线，如图4、5所示。可见，随着激励频率的增加，金属橡胶试件的存储模量减小，损耗模量呈波动状态。

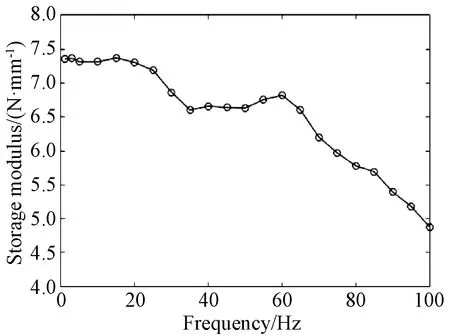
图4 不同频率下存储模量的变化Fig.4 Change of storage modulus at different frequencies

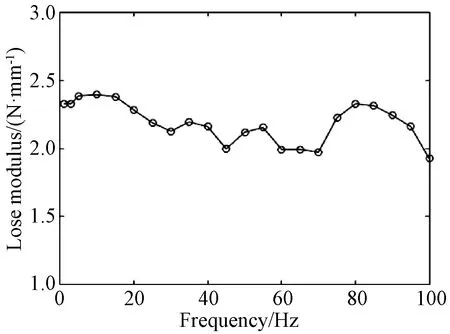
图5 不同频率下损耗模量变化Fig.5 Change of lose modulus at different frequencies

3 金属橡胶动态特性的分数阶导数模型的建立

3.1 黏弹性力模型

金属橡胶是一种黏弹性材料，描述黏弹性材料的标准流变学模型是由弹簧和Newton粘壶的串并联组成的本构模型。最基本的标准流变学模型有弹簧和Newton粘壶串联构成的Maxwell模型以及它们的并联构成的Kelvin-Voigt模型[8]。将一个Kelvin-Voigt模型与弹簧串联，或将一个Maxwell模型与弹簧并联，形成的黏弹性本构模型称为经典三元固体模型，图6所示为一个Kelvin-Voigt模型与弹簧串联构成的经典三元固体模型。这种模型表达的力-位移关系为：

(1)

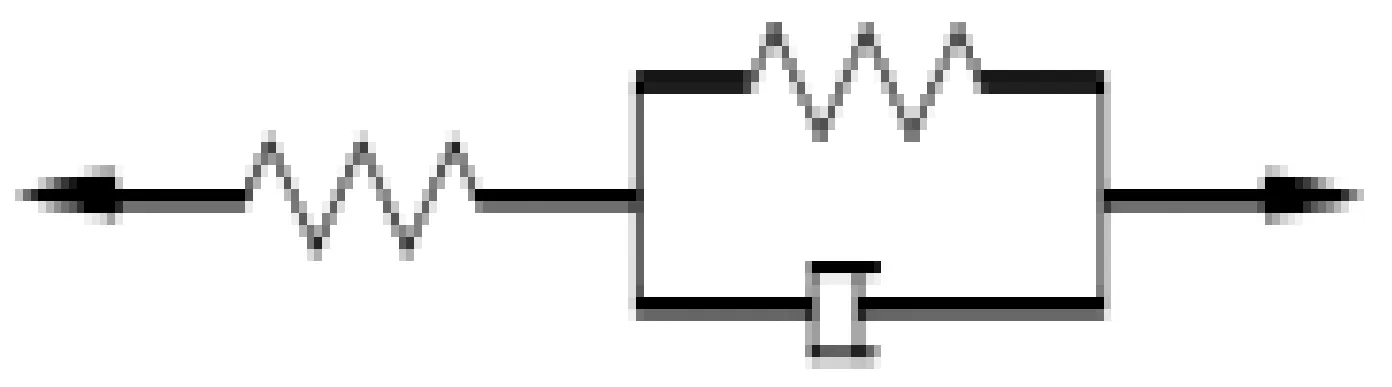
图6 经典三元固体模型Fig.6 Classical ternary model

在常见的标准流变学模型基础上，Gemant首先提出了分数导数模型[9]，用Abel体代替标准流变学模型中的Newton粘壶。Abel体的本构关系为：

(2)

式中：b为粘性系数，Dα为分数导数算子，α为导数阶次。当b值一定时，若α值无限接近1，则Abel体的变形接近于弹性体；若α值无限接近0，则Abel体的变形接近于粘性体；若α值在0和1之间，则Abel体的变形既有弹性材料的形变特点，也有粘性材料的形变特点，可见Abel体更适合描述真实材料的形变[10]。将经典三元固体模型中的Newton粘壶用Abel体代替，得到分数阶三元模型，如图7所示，该模型所表达的力-位移关系为：

Fve(t)+p1DαFve(t)=q0x(t)+q1Dαx(t)

(3)

式中：p1，q0，q1为材料参数，α为粘性系数，Dα为分数导数算子。

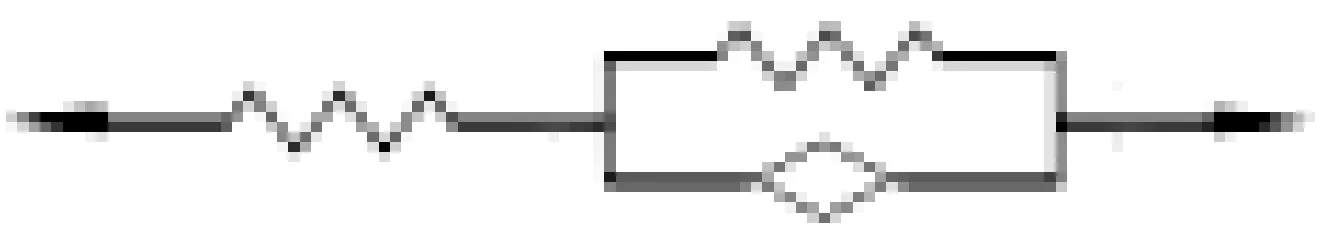
图7 分数阶三元模型Fig.7 Fractional ternary model

分数阶导数具有不同的定义，应用最广泛的有Riemann-Liouville定义和Grünwald定义。由于Grünwald定义在函数应用上的限制较少，本文采用Grünwald定义对分数阶导数进行数值计算[11]，即：

Dαg(t)=

(4)

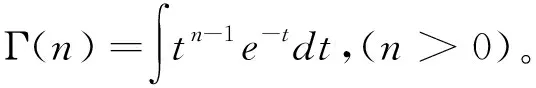
3.2 金属橡胶动态特性探讨

金属橡胶是一种均质多孔弹性材料，其内部结构是金属丝之间相互嵌合、勾连而形成的类似于橡胶分子结构的空间网状结构。不仅具有类似于橡胶的高弹性、大阻尼特性，而且具有金属的抗腐蚀、抗辐射、耐高低温等特性。当其作为减振元件工作时，金属橡胶表现出黏弹性材料的特性，其位移-恢复力迟滞曲线如图3所示。用分数阶三元模型描述的黏弹性力-位移曲线如图8(a)所示，可见分数阶模型为线性模型，用图3中迟滞曲线对应的数据依次减去图8(a)中迟滞曲线对应的数据并取平均值，作为非线性力数据。

金属橡胶迟滞曲线的形成不仅包括黏弹性力的影响，还包含了非线性弹性力部分，故在表述其迟滞恢复力时，要同时考虑到黏弹性力和非线性弹性力，如图8所示。金属橡胶材料弹性恢复力中含有较强的位移三次非线性因素，非线性弹性力Fe(t)可以表示为：

Fe(t)=kex3(t)

(5)

故金属橡胶迟滞恢复力可表示为：

F(t)=Fve(t)+Fe(t)

(6)

其中，Fve(t)为黏弹性力，Fe(t)为非线性弹性力。

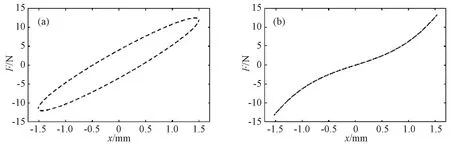
图8 金属橡胶迟滞恢复力分解 (a)黏弹性力-位移； (b) 非线性力-位移Fig.8 Resolution of force-displacement curve of metal rubber(a) viscoelastic force-displacement; (b) nonlinear force-displacement

4 参数识别

4.1 非线性弹性力模型单元参数识别

金属橡胶材料具有非线性[12]，本研究采用最小二乘法识别非线性弹性力模型参数。由试验得到金属橡胶试件在频率10 Hz，振幅为1 mm时的迟滞曲线。对非线性弹性力进行拟合，得到的金属橡胶试件力-位移曲线见图9。拟合结果ke=1.7718，误差为7.5%，可见该三次非线性表达式(式(5))能够较好地描述金属橡胶材料的非线性弹性力。

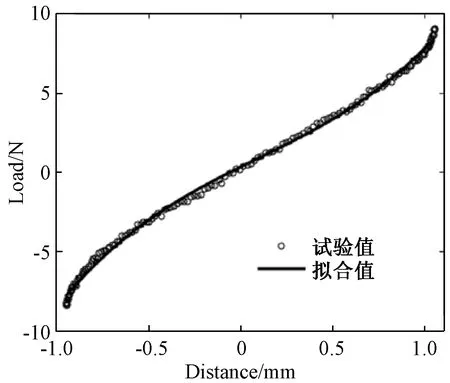
图9 非线性弹性力模型与试验值的对比Fig.9 Comparison of test and calculation results of nonlinear elastic force

4.2 黏弹性模型单元参数识别

材料的黏弹性动态力学特性通常可以用存储模量和损耗模量来描述，为了便于计算，将分数阶导数模型从时域变换到频域进行参数识别[13]。在零初始条件下，对分数阶三元模型的力-位移关系进行傅里叶变换可以得到：

fve(w)+(iw)αp1fve(w)=q0x(w)+(iw)αq1x(w)

(7)

根据刚度与载荷的关系：

fve(w)=k(w)x(w)=(k′(w)+jk″(w))x(w)

(8)

则动刚度为：

(9)

将iα=cos(πα/2)+isin(πα/2)代入式(9)，进行实部与虚部的分离，可以得到动刚度实部(即存储模量)k′(w)、动刚度虚部(即损耗模量)k″(w)和损耗因子tanδ如下：

(10)

(11)

(12)

当α=1时，式(9)～(12)表示经典三元模型中材料的动态特性参数。当0<α<1时，式(9)～(12)表示分数阶三元模型中材料的动态特性参数。利用试验测得的金属橡胶试件在频率为1～100 Hz、振幅为1 mm的外加激励下的复刚度，采用最小二乘法对参数进行识别，试验与计算的复刚度误差为：

(13)

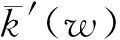
表1 参数识别结果Table 1 Parameters identification results

图10 黏弹性力模型与试验值的对比Fig.10 Comparison of test and calculation results of viscoelastic force

表2 黏弹性力模型与试验的相对误差Table 2 Relative error of test and calculation results of viscoelastic force

5 模型验证

通过对经典三元模型和分数阶三元模型的参数识别，可知分数阶三元模型能够较好地描述金属橡胶的存储模量、损耗模量等动态特性。为了进一步说明分数阶三元模型的适用性，对模型在不同振幅激励下的结果进行验证。

迟滞曲线是金属橡胶加载和卸载过程中恢复力的变化曲线，能够描述材料的动态特性[15]。如图11所示，根据振幅分别为0.5，1和1.5 mm时拟合的数学模型重构试验迟滞曲线，检验不同工况下分数阶模型计算值与试验值的吻合程度。振幅为0.5，1和1.5 mm时，试验值与分数阶模型的均方根误差分别为2.63，3.39，4.26。可见，在不同振幅下，分数阶模型都可以较好地拟合迟滞曲线；且随着振幅减小，对迟滞曲线的拟合误差更小，拟合效果越好。可见分数阶模型能够用较少参数准确地描述金属橡胶的动态特性。

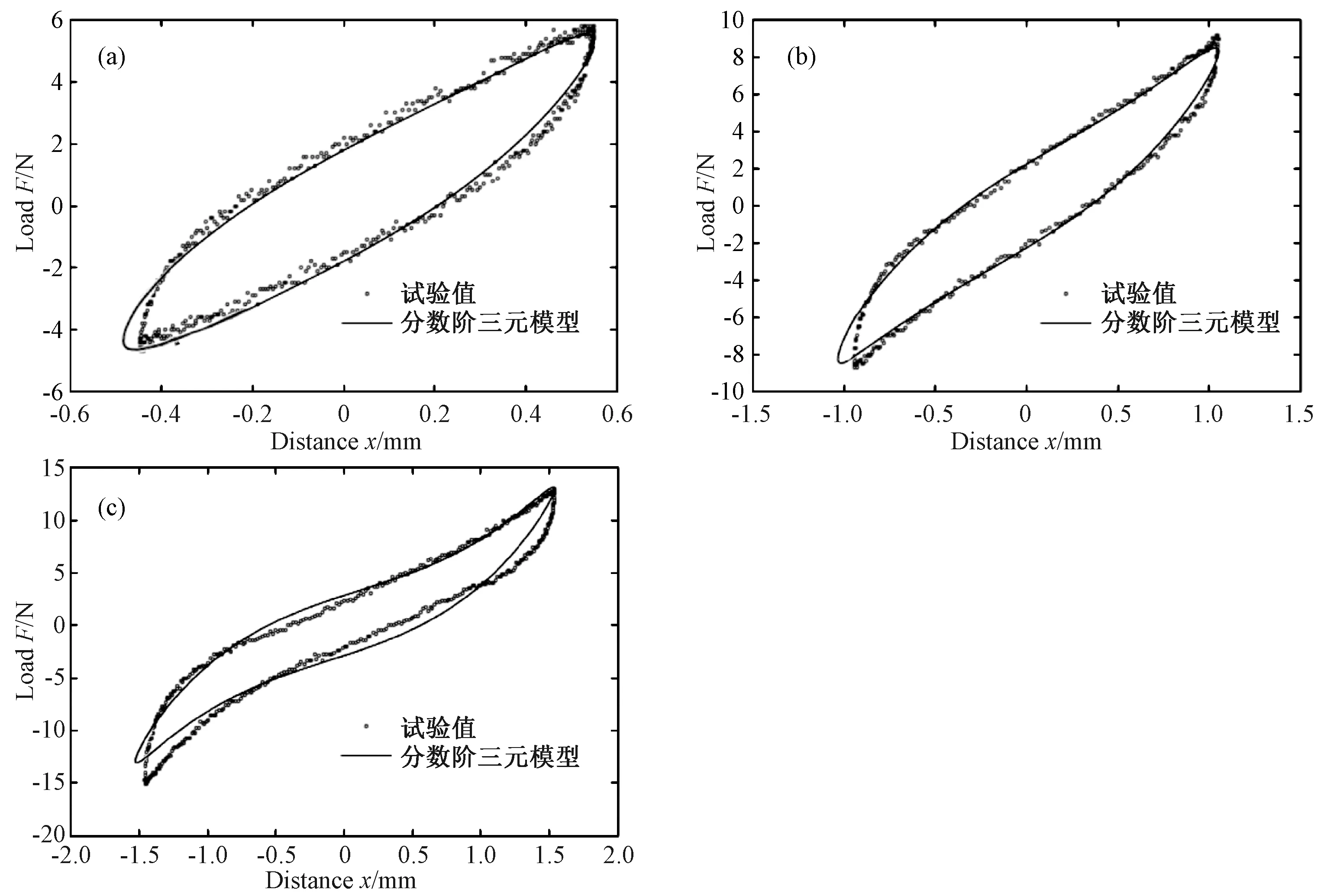
图11 不同振幅下金属橡胶迟滞曲线(a)a=0.5 mm; (b) a=1 mm; (c) a=1.5 mmFig.11 Force-displacement curve of metal rubber under different amplitude (a) a=0.5 mm; (b) a=1 mm; (c) a=1.5 mm

6 结 论

本研究分别采用分数阶三元模型和经典三元模型与非线性弹性力模型并联叠加构造金属橡胶动力学模型，结合金属橡胶动态特性试验进行参数识别与模型验证。结果发现用三次非线性关系可以很好地描述金属橡胶动力学特性中的非线性因素；在描述存储模量和损耗模量等动态特性时，经典三元模型几乎无法准确进行描述，而分数导数模型能够在较少参数的情况下较精确地描述金属橡胶的动态特性；在不同振幅下，分数阶模型都可以较好地拟合金属橡胶迟滞曲线。由此可见，分数阶导数的引入可以使模型更好地描述金属橡胶的动态特性，具有较好的工程实用性。