屈曲T 型振动能量采集器压电性能对比

陶胜晖，张志浩

（江苏科技大学 船舶与海洋工程学院，江苏镇江 212003）

0 引言

振动能量是环境中普遍存在的一种能源。振动型能量采集器是一种能将环境中的振动能转化为电能的设备，可用于无线传感器节点等小型电子元件供电，代替化学电池[1-2]。压电式振动能量采集器的工作原理是基于压电材料的压电效应，在外力作用下，压电层产生应力应变导致内部电荷的定向流动而形成电流。与其他类型的振动能量采集技术相比，压电振动能量采集器具有结构简单、无污染、寿命长、微型化、集成化和能量密度高等诸多优点，备受关注[3-6]。

在过去几十年中，国内外众多学者对于压电振动能量采集器的研究已经获得了实质性的效果。2006年，ERTURK等[7]建立了轴向预压力压电振动能量采集器。2018年，张智娟等[8]以双晶压电片为研究对象，设计了一种可收集电动机机械振动能量的双压电振动能量采集器。王祖尧等[9]研究了通过添加线性振子的磁悬浮非线性能量器采集系统在多频激励下的非线性动力学。张庆新等[10]利用磁控形状记忆合金（MSMA）逆效应设计了一种新型高效振动能量采集器，建立并分析了振动能量采集器的结构模型，对采集器的各部分结构进行了理论分析与计算。

有限元分析方法是在结构分析与设计中被广泛使用的一种功能强大的分析方法。2015年，HE等[11]用有限元法讨论了系统参数对双稳态能量采集器输出功率的影响。胡世军[12]通过有限元分析法对不同情况下悬臂梁发电性能进行研究。2017年，PAN等[13]通过静态有限元分析计算并分析了不同铺层宽度和混合宽度的BPEH的稳定构型和纵向曲率引起的初始电压。2019年，郭鑫源等[14]通过有限元法研究悬臂梁基板尺寸变化对压电片发电特性的影响。

目前，对悬臂梁压电振动能量采集器的研究已日趋成熟，但是悬臂梁型能量采集器的采集频率相对较低。因此，学者们开始研究具有更大采集频率宽度、发电效益更好的模型。为探讨不同形状的压电梁对采集频率的拓展效果，以增大发电效率，本文设计屈曲T型压电梁振动能量采集器，通过ANSYS软件中结构-电耦合场研究激振状态下不同模型尺寸工况中T型梁能量采集器发电特性的改变趋势，并与相同规格悬臂梁发电特性进行比较分析，为屈曲T型压电梁振动能量采集器的设计提供理论依据。

1 ANSYS前处理

1.1 结构与单元

压电陶瓷晶体片是具有机电耦合特性的材料。本文通过ANSYSMechanical APDL软件所具备的耦合场分析功能来进行压电陶瓷晶体片PZT[15]与基板结构之间的复合结构-电场耦合分析。根据基板以及压电陶瓷片的物理及电学方面的不同属性，选择SOLID186固体结构单元进行基板的属性模拟，选择SOLID5耦合场6面体单元对压电陶瓷片PZT进行属性模拟。

本文所适用的振动能量采集器由2块基板以及压电陶瓷片PZT所组成。能量采集器的尺寸数值以及各结构参数如表1所示。

压电陶瓷晶体片刚性系数矩阵C(×10 GPa)为

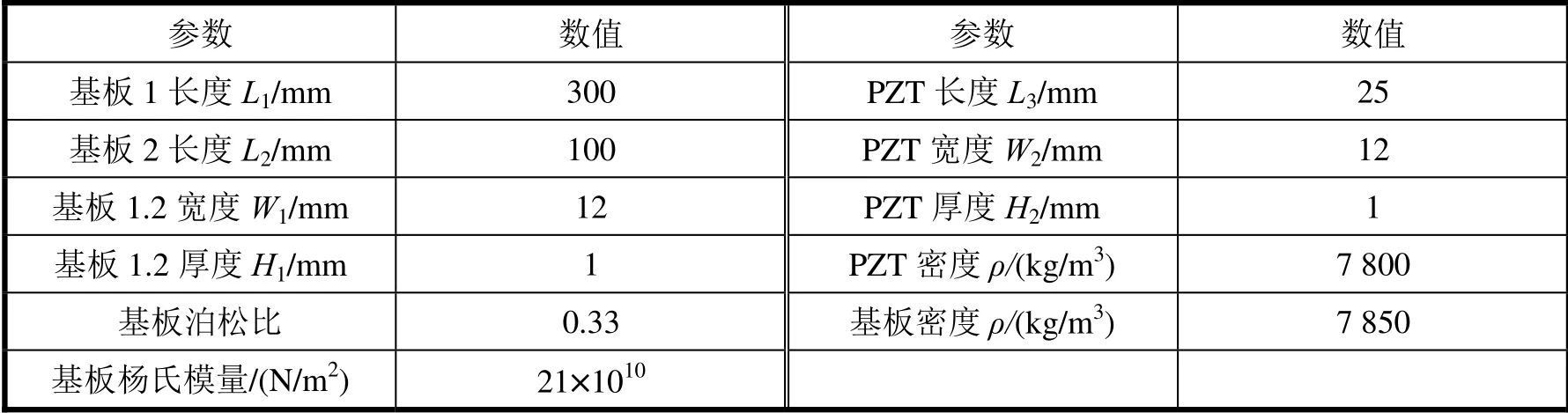
表1 屈曲T 型振动能量采集器结构参数

通过ANSYS软件前处理模块中自由网格划分法对已建立的实体模型进行网格划分。模型结构与网格示意图如图1所示。

1.2 工况选取

为研究不同尺寸对屈曲T型振动能量采集器的影响效果，分别研究改变基板长度、基板宽度时电压值随激振频率的变化趋势，基板的尺寸变化如表2所示。

图1 屈曲T 型振动能量采集器示意图

表2 工况情况表

1.3 模态分析

通过模态分析可测得模型的固有频率和振型。屈曲T型振动能量采集器的模态分析结果如图2所示。

图2 模态示意图

邓冠前[16]曾于2008年进行悬臂梁压电振子发电研究，获得压电振子所产生的电压与振动频率变化之间的规律。本文在此基础上，对相同模型进行ANSYS软件数值模拟，并将所得结果与试验数据进行对比，如图3和图4。

由图4可知：数值模拟所得结果曲线相比试验结果更顺滑，变化趋势相对平缓，但模拟结果与试验数据整体上趋势相同，说明数值模拟具有一定的准确性。

3 谐响应分析

在支座Z轴（垂直于基板1）方向施加大小为2.5 m/s2的加速度激励，通过改变激励信号的频率即可得到输出电压值随着激励信号频率变化而变化的规律。

图3 试验测试系统

图4 实验数据与数值模拟结果对比

3.1 基板长度对输出电压值的影响作用

不同基板长度下电压值随频率变化曲线如图5所示。

图5 不同基板长度下电压值随频率变化趋势

图5 不同基板长度下电压值随频率变化趋势

图5显示了悬臂梁以及T型梁不同基板长度下电压值随着激励信号频率的变化趋势。从图5(a)与图5(b)可以观测到，悬臂梁与T型梁基板长度对电压值峰值的影响效应相同，电压值的峰值大小随着基板长度的增大而增大，且达到电压峰值时的频率值随之减小。

对比图5(a)与图5(b)可以发现，T型梁1阶模态激振下所测得电压峰值要稍大于悬臂梁的电压值，达到峰值的频率值更小，T型梁电压值-频率曲线存在第2个电压峰值，采集频率宽度相对于悬臂梁得到较大的提升。T型梁2阶模态激振下电压峰值的大小基本不变，测得电压峰值的频率值随着基板长度的增大而减小。

3.2 基板宽度对输出电压值的影响作用

不同基板宽度下电压值随频率变化趋势如图6所示。

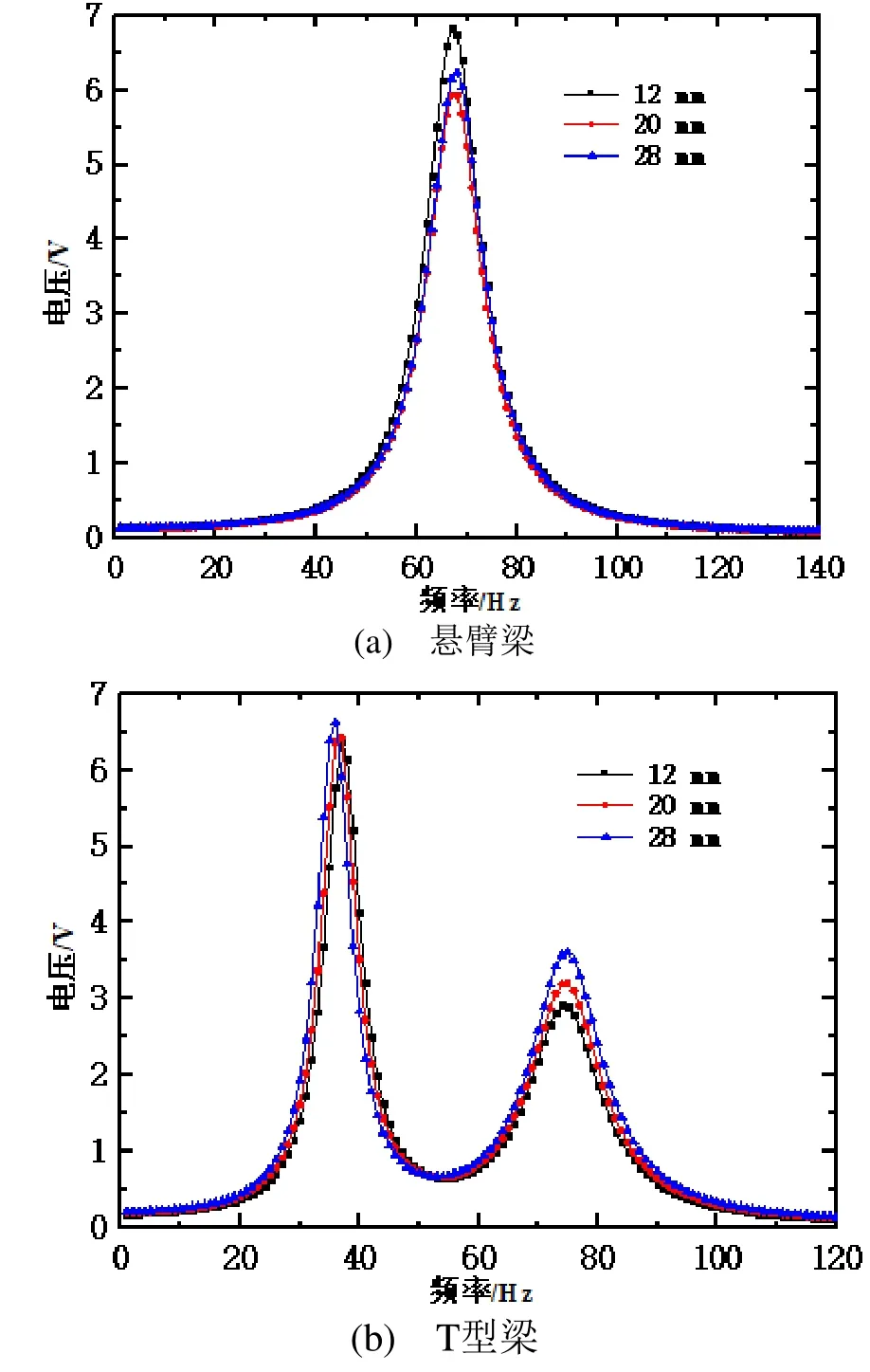
图6 不同基板宽度下电压值随频率变化趋势

图6显示了悬臂梁以及T型梁不同基板宽度下电压值随着激励信号频率的变化曲线。从图6可以看出，基板宽度对电压值变化的影响相对于长度所带来的影响效果而言并不强烈。

对比图6(a)与图6(b)可以发现：T型梁1阶模态激振下所测得电压峰值要稍大于悬臂梁的电压值，达到峰值的频率值更小；T型梁电压值-频率曲线存在第2个电压峰值，采集频率宽度相对于悬臂梁得到较大的提升，这与长度作用下的电压值-频率曲线变化规律相同；悬臂梁测得电压峰值的频率值不变，而T型梁测得电压峰值的频率值随着基板宽度的增大而减小。

4 结论

本文对屈曲T型振动能量采集器在进行模态分析和谐响应分析。对不同结构参数的变化对电压值-频率曲线的影响进行研究，并与悬臂梁结构进行对比。本文针对屈曲T型压电梁振动能量采集器进行模态以及谐响应分析，研究T型梁在不同约束情况下电压值-频率曲线的变化规律，并与悬臂梁结构进行对比。结果表明：谐响应分析中，振动能量采集器的输出电压与基板长度成正比；基板宽度越大，输出电压峰值随着增大，增长幅度相对较小；对比T型梁与悬臂梁可以发现，T型梁结构电压值-频率曲线1阶模态激振频率处峰值大于悬臂梁，且T型梁电压值-频率曲线在2阶模态激振作用下出现第2个峰值，T型梁采集频率宽度大于悬臂梁。

通过对比分析可以看出：T型梁相比于悬臂梁拥有更宽的采集幅频宽度，T型梁受到相同谐和载荷作用时所测得电压峰值大于悬臂梁，说明T型梁相比于悬臂梁是更优良的振动能量采集器模型。在已分析的基础上再通过瞬态分析对谐响应分析的结果进行比对，而非线性静力、谐响应以及瞬态分析下T型梁得到的电压值变化规律有待继续研究。