控氮304不锈钢热变形过程中的动态再结晶行为研究
2021-03-08任伟吴冰洁邱阳王晓童李梅娥
任伟,吴冰洁,邱阳,王晓童,李梅娥
(1.西安交通大学金属材料强度国家重点实验室,710049,西安;2.中国核动力研究设计院核反应堆系统设计技术重点实验室,610200,成都)
304奥氏体不锈钢是一种应用广泛的耐蚀钢,但它在加工及服役过程中易沿晶界析出碳化物,降低材料耐蚀性能。氮与镍具有扩大奥氏体相区的作用,通过降低奥氏体不锈钢的含碳量并加入适量的氮,可提高钢的强度及耐晶间腐蚀性能。这种钢称为控氮304不锈钢,由于其具有良好的综合力学性能、耐中子辐照脆化性能及耐腐蚀性能,大量用于压水堆堆内构件[1]。这些堆内构件主要包括各种锻件及板材、棒材和管材的加工成形件,它们都要经历锻造、挤压和轧制等热塑性成形过程,而热塑性成形过程中普遍存在的动态再结晶现象会引起变形金属的组织变化,从而影响材料的物理、化学性能。由于奥氏体不锈钢在热加工过程中几乎不发生相变,再结晶就成为影响其最终组织的决定性因素,因此研究其在热变形过程中的动态再结晶行为对于控制成形工艺、获得细小均匀的晶粒组织具有重要意义。
由于奥氏体不锈钢动态再结晶现象的重要性,国内外学者进行了大量研究[2-8]。Wang等研究了奥氏体不锈钢在不同应变速率下孪晶演化及其对动态再结晶的影响[2];Wahabi等研究了初始晶粒尺寸对动态再结晶规律的影响[3];Marchattiwar等研究了304奥氏体不锈钢动态再结晶动力学[4];Kim等对304不锈钢进行了热扭转实验,根据实验结果确定了不同条件下的峰值应力、稳态应力等,并采用Avrami方程分析了动态再结晶的动力学[5],Dehghan-Manshadi等通过单道次及双道次热扭转实验研究了304不锈钢在动态再结晶及后动态再结晶中的力学行为及组织演化特征[6];Stewart等研究了杂质元素的偏析对动态再结晶现象出现时间的影响[7];廖喜平等通过热压缩实验研究了304不锈钢的流动应力模型及热加工图[8]。针对控氮304不锈钢动态再结晶现象的系统性研究迄今尚未见报导。
本文利用热力模拟机对控氮304不锈钢进行了热压缩实验,通过对实验结果的理论分析,建立了控氮304不锈钢的热变形流动应力模型,并对热变形过程中的组织演化及动态再结晶动力学行为进行分析,为该材料热成型过程的工艺优化提供了参考。
1 实验方法
实验材料控氮304不锈钢的化学成分见表1。先将实验材料机械加工成Φ10 mm×15 mm的圆柱形试样。热压缩过程中变形温度分别为900、1 000、1 100、1 200 ℃时,每个不同变形温度下的应变速率分别为0.001、0.01、0.1、1 s-1。实验设备为Gleeble3800热力模拟机,热压缩实验工艺曲线如图1所示,试样以5 ℃/s的升温速率加热至1 250 ℃并保温3 min,再以10 ℃/s的速率降温至变形温度后保温1 min,使组织均匀,再以预定应变率进行热压缩,最大应变值为0.7。试样压缩完后立即水淬以保留其组织,然后将试样沿压缩方向对半切开,取一半进行打磨、抛光,腐蚀剂采用50 ml浓盐酸和5 ml双氧水配制,在常温下腐蚀20~25 s,即可进行金相观察和组织分析。
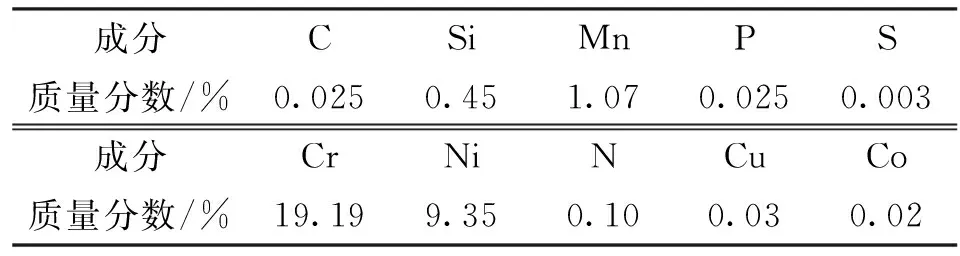
表1 控氮304不锈钢的化学成分
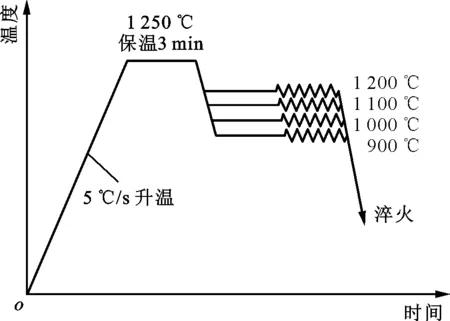
图1 热压缩实验工艺曲线
2 实验结果及分析
2.1 流动应力曲线
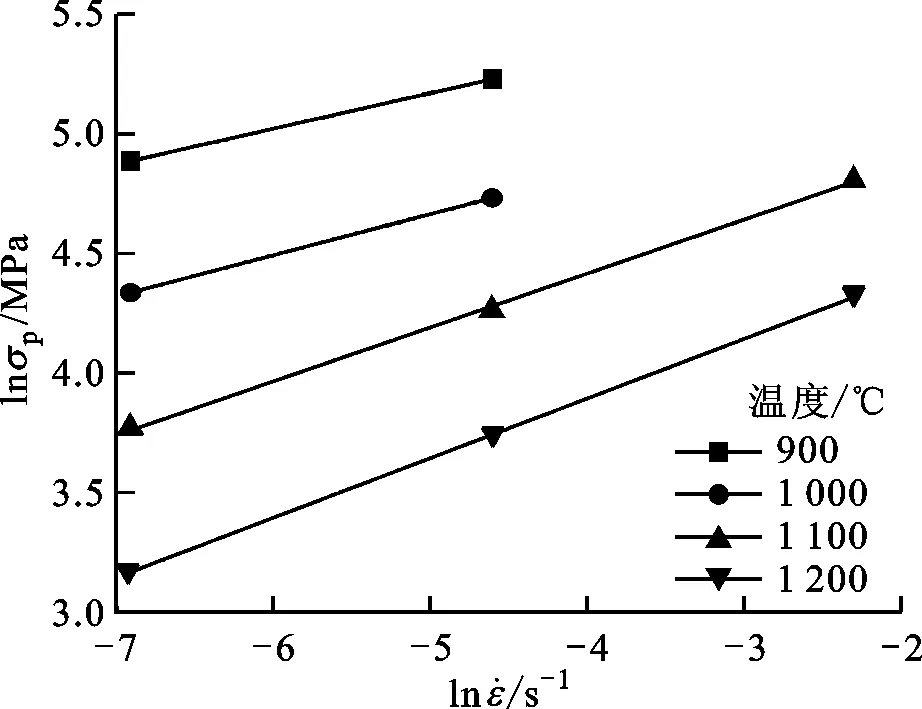
图2给出了实验得到的16个变形条件下的部分流动应力σ曲线,ε为变形过程中的应变。图2a为1 200 ℃时不同应变速率下的流动应力曲线,图2b为应变速率0.01 s-1时不同温度下的流动应力曲线。热变形开始后,由于加工硬化的作用,流动应力先随着应变的增加而快速增大,随后由于动态回复及动态再结晶的软化作用,应力增速减慢,当加工硬化与动态软化作用达到平衡时,应力达到峰值;随着应变继续增大,动态再结晶软化作用增大,应力出现下降,直至达到稳态时,硬化作用与软化作用两者又再次达到平衡。可以看出,变形温度一定时,流动应力随应变速率增大而增大,峰值应力对应的应变也增大;应变速率一定时,流动应力随温度的降低而增大,峰值应力对应的应变也增大。这是因为应变速率较低时,有较充分的时间进行动态再结晶晶粒的形核及长大,故软化作用强,温度较高时,则由于原子具有较高的活性而具有同样的效果。
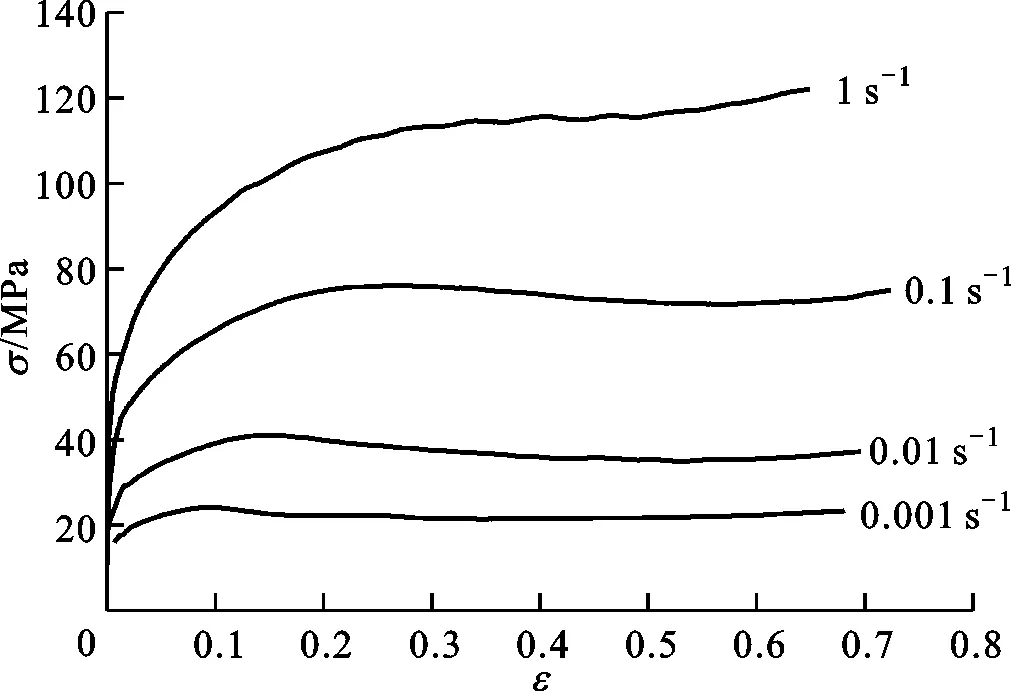
(a)T=1 200 ℃
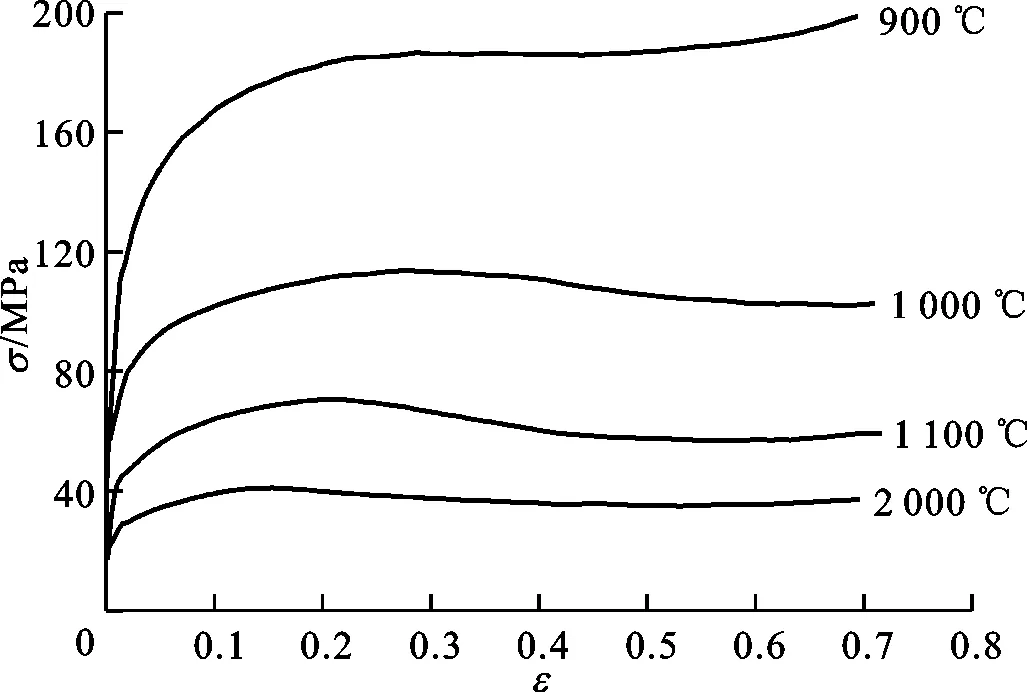
图2 控氮304不锈钢不同变形条件下的流动应力曲线
2.2 临界应力σc及饱和应力σs的确定
图3中σDRX为典型动态再结晶流动应力曲线,发生动态再结晶的临界应变及临界应力分别为εc和σc,动态再结晶达到稳态时的应力为σss,σDRV为相应的假定仅有动态回复而无动态再结晶时的流动应力曲线,达到稳态时的应力为饱和应力σs,两条曲线之间的差值Δσs为动态再结晶导致的软化效应。临界应力σc及饱和应力σs都是分析动态再结晶行为的重要特征参数,但不能直接从实验曲线获得。本文采用Poliak和Jonas[9]提出的方法,先根据流动应力曲线求出加工硬化率θ(θ=dσ/dε),并画出θ-σ曲线,如图4、图5a、5c所示,该曲线与θ=0的两交点分别为峰值应力σp和稳态应力σss,临界应力对应θ-σ曲线上的拐点,但由于拐点的准确位置很难从该图直接确定,故而对该曲线再次求导,并画出(-dθ/dσ)-σ曲线,如图5b、5d所示,该曲线极小值点对应应力即为临界应力。得到临界应力后,将θ-σ曲线从临界点(σc,θc)处反向线性外插,外插直线与θ=0的交点即为饱和应力。
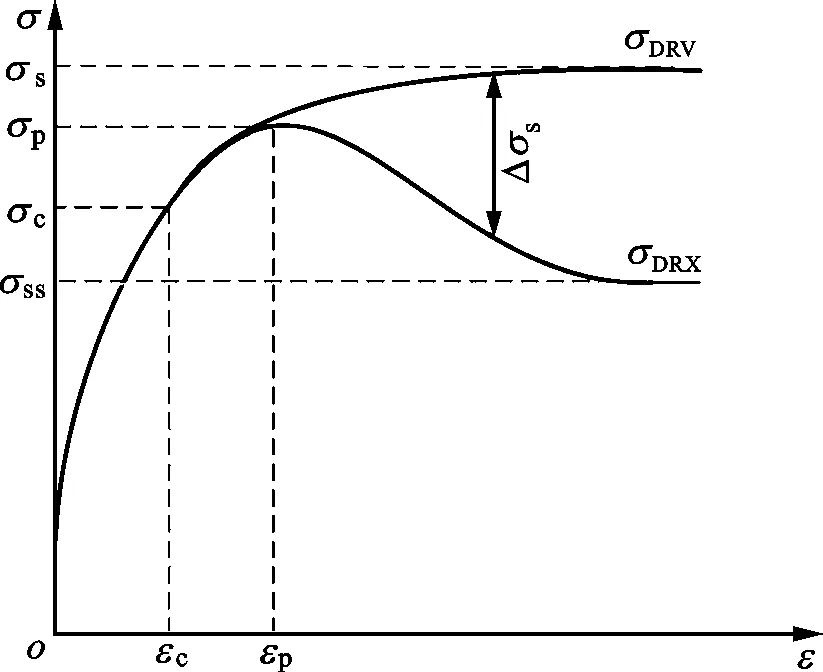
图3 动态回复与动态再结晶流动应力曲线
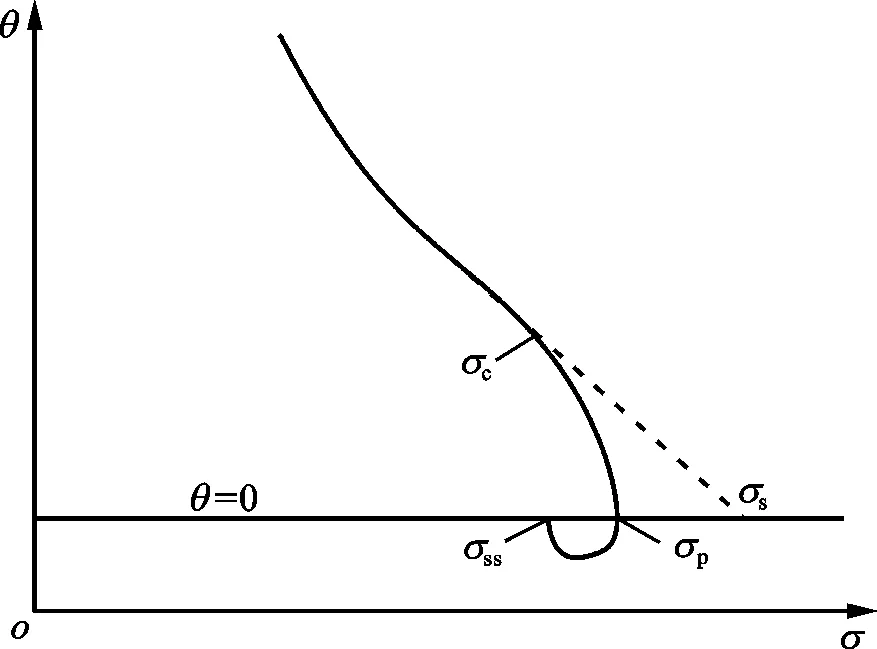
图4 加工硬化率曲线及特征值求解示意图
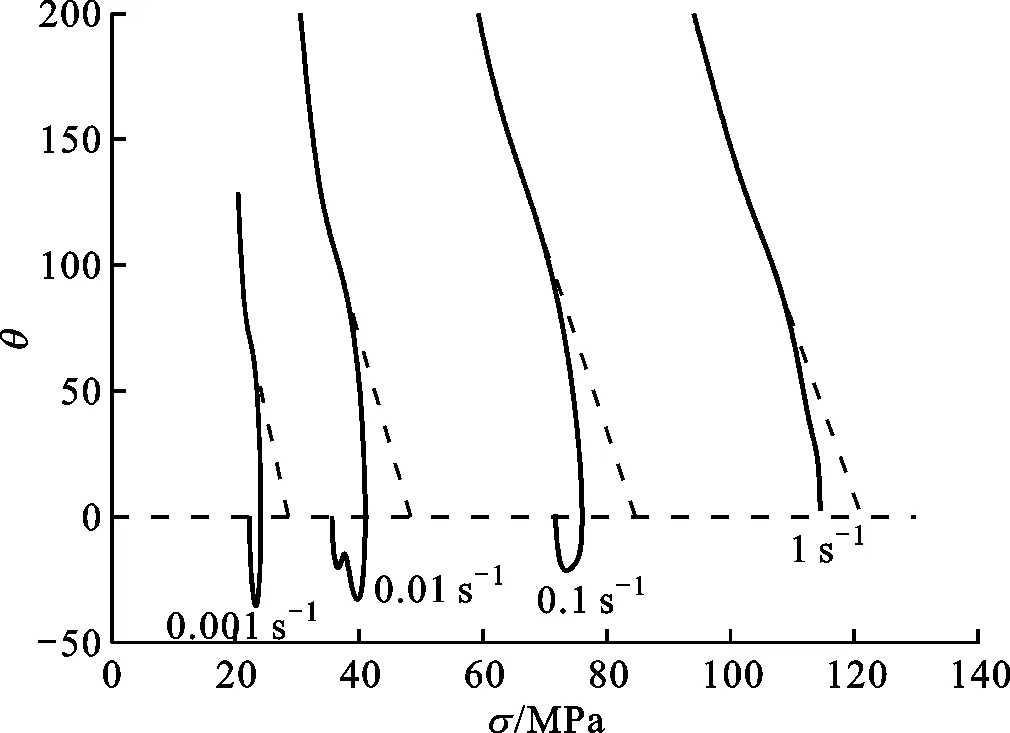
(a)T=1 200 ℃时θ-σ曲线
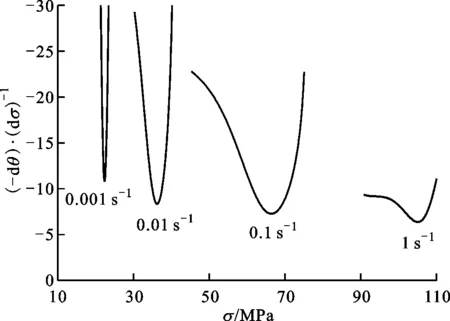
(b)T=1 200 ℃时(-dθ/dσ)-σ曲线
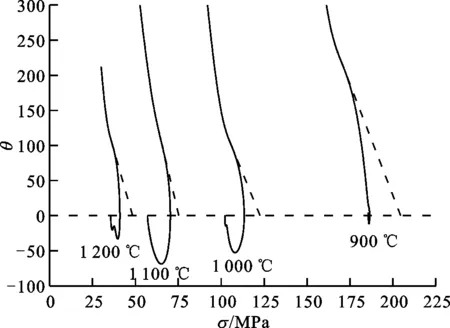
时θ-σ曲线

时(-dθ/dσ)-σ曲线图5 不同变形条件下的加工硬化率曲线及(-dθ/dσ)-σ曲线
2.3 流动应力模型的建立
2.3.1 加工硬化与动态回复的描述 材料在热变形过程中的加工硬化与动态回复效应可以用Estrin-Mecking模型[10]描述,该模型给出了位错密度随应变的变化关系
(1)
式中:h和r分别为加工硬化系数及动态回复软化系数。Bergstrom也曾提出类似的模型[11]。
引入初始条件ε=0,ρ=ρ0为初始位错密度,对上式积分可得
(2)
流动应力与位错密度的关系可表示为[12]
(3)
式中:α为材料常数;μ为剪切模量;b为柏氏矢量。结合式(2)(3),得到
(4)
式中σ0为初始应力。当应变ε趋于无穷大时,σ=σs,即
(5)
将式(5)代入式(4)即可得到只有动态回复时的应力应变关系[13]
(6)
式(6)对应图2中σDRV曲线,既用于描述应变小于临界应变εc时的流动应力曲线,也用于确定应变大于临界应变后发生动态再结晶时的流动应力曲线。
2.3.2 动态再结晶动力学 热变形过程中当应变超过临界应变时会发生动态再结晶,研究表明,描述静态再结晶动力学的Avrami关系式也可用于动态再结晶动力学过程[13-14],研究者们提出了各种不同的具体形式,本文采用的模型形式为[15-16]
X=1-exp(-kd((ε-εc)/εp)nd)
(7)
式中:X为动态再结晶分数;kd和nd为与材料有关的参数。由2.2节分析可知,动态再结晶导致的软化效应Δσs=σDRVσ,Δσs的最大值为(σs-σss),所以动态再结晶分数又可用软化分数表示为
(8)
综合以上两式可得
σ=σDRV-(σs-σss)(1-
exp(-kd((ε-εc)/εp)nd))ε≥εc
(9)
式(9)用于描述应变大于临界应变εc后的动态再结晶流动应力曲线。
2.3.3 模型参数的确定 以上得到的流动应力模型利用了σs、σss、εc等特征参数,并引入了r、kd、nd等模型参数,为确定特征参数及模型参数与变形条件的关系,需要用到Sellars等的双曲正弦模型[17]
(10)
(11)
(12)
(13)
将不同变形条件下的σp进行线性拟合,如图6所示,可求得n1=5.025 1,β=0.058 75,α=β/n1=0.011 69,n=3.681 9,Qact=385.755 kJ/mol。
由此可以得到Z的表达式
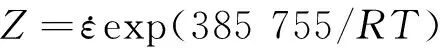
(14)
将各特征值σs、σss、εc、εp与Z进行拟合,如图7所示,根据拟合结果可得Z与各特征值的关系式为
σs=85.543 2arsinh(4.457 7×10-4Z0.266 1)
(15)
σss=85.543 2arsinh(2.918 2×10-4Z0.273 4)
(16)
εc=5.662 5×10-3Z0.096 2
(17)
关系

关系

关系
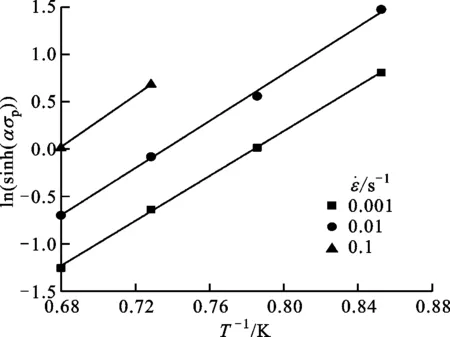
(d)ln(sinh(α σp))-1/T关系图6 n1、β、n及热变形激活能Qact的确定
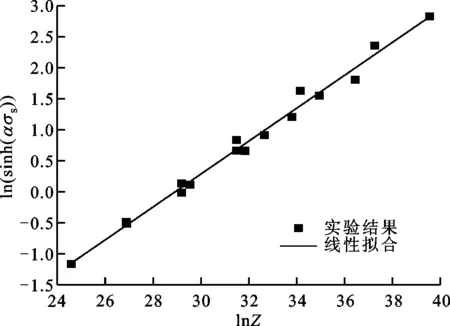
(a)ln(sinh(α σs))-lnZ关系
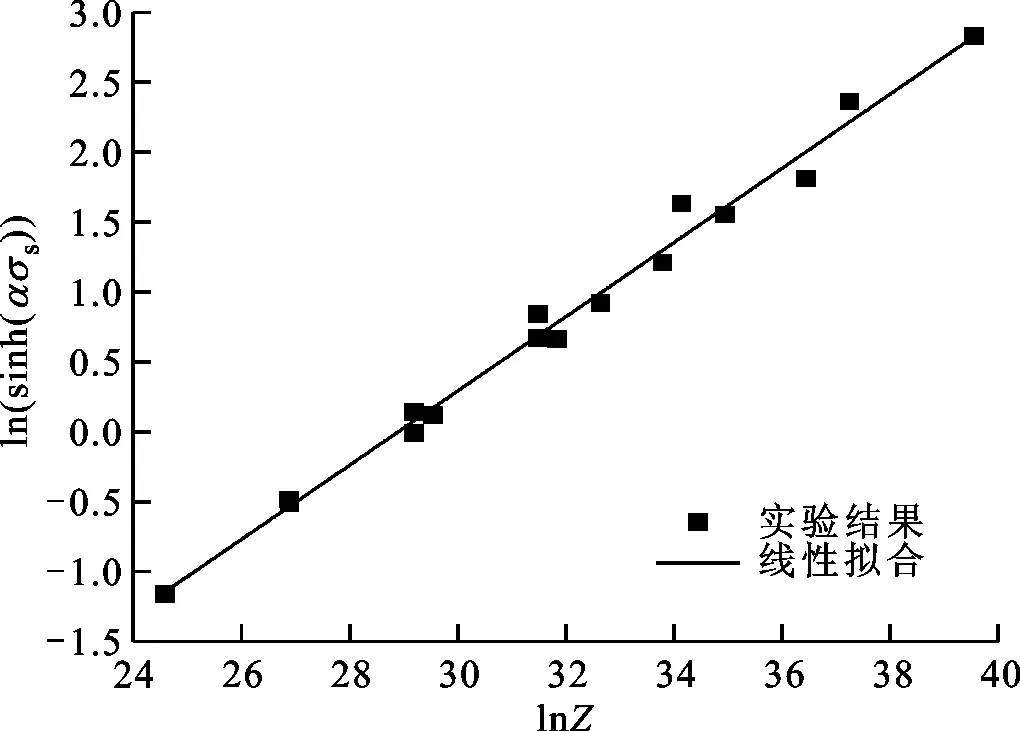
(b)ln(sinh(α σs))-lnZ关系
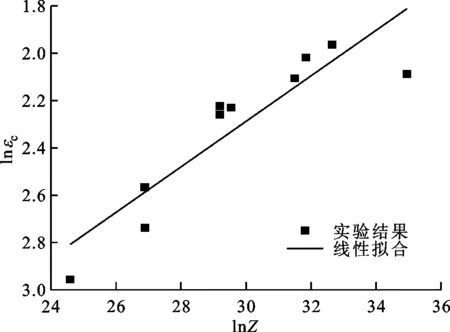
(c)lnεc-lnZ关系

(d)lnεp-lnZ关系图7 σs、σss、εc、εp与Z的关系
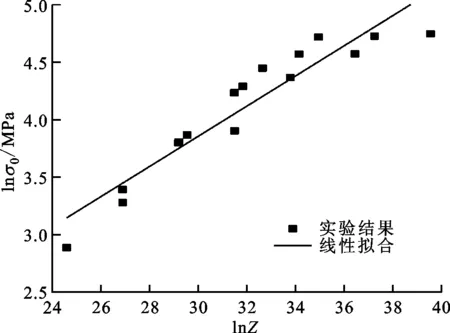
图8 σ0与Z的关系
(18)
取应变为2%时的应力作为初始应力σ0,根据图8的拟合结果,得到σ0的拟合关系式为
σ0=0.835 2Z0.131 2
(19)
为求h参数和r,对式(6)进行微分
(20)
式(20)与式(6)相乘可得
(21)
(22)
通过绘制σθ与σ2的线性关系图,确定其斜率(-0.5r)可求得动态回复系数r,再通过式(5)可求得加工硬化系数h。拟合实验结果如图9所示,可以得到h、r的拟合关系式
h=3.089×1010Z0.305 7
(23)
r=16.060 9Z-0.029 57
(24)
根据式(7)变形可得下式
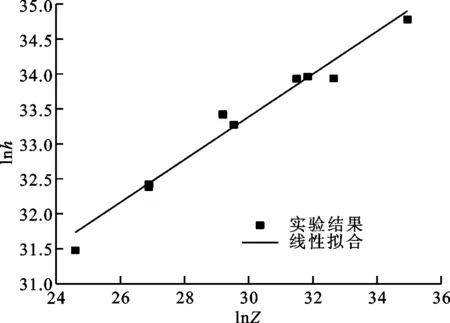
(a)lnh-lnZ关系
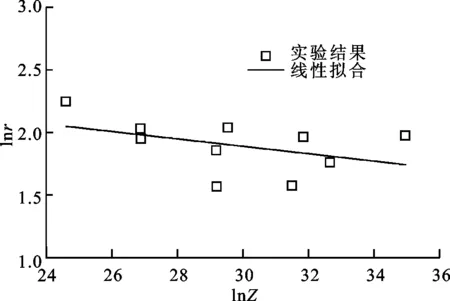
(b)lnr-lnZ关系图9 h、r与lnZ的关系
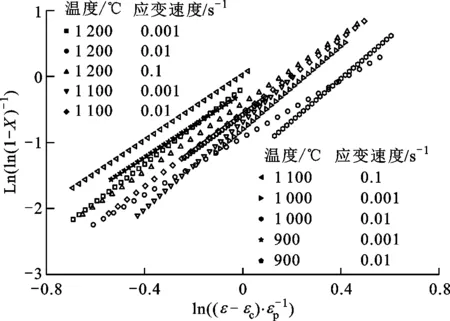
图10 不同变形条件下数据拟合确定kd与nd
(25)
由式(25)可得,以ln(ln(1/(1-X)))-ln((ε-εc)/εp)关系作图,如图10所示,线性拟合后可求得nd的平均值为2.794 1,kd为0.606 6,故动力学方程为
X=1-exp(-0.606 6((ε-εc)/εp)2.794 1)
(26)
最终得到控氮304不锈钢在热变形过程中的流动应力模型如下
(27)
给定变形温度及变形速率,即可由式(6)和式(9)预测出流动应力曲线。
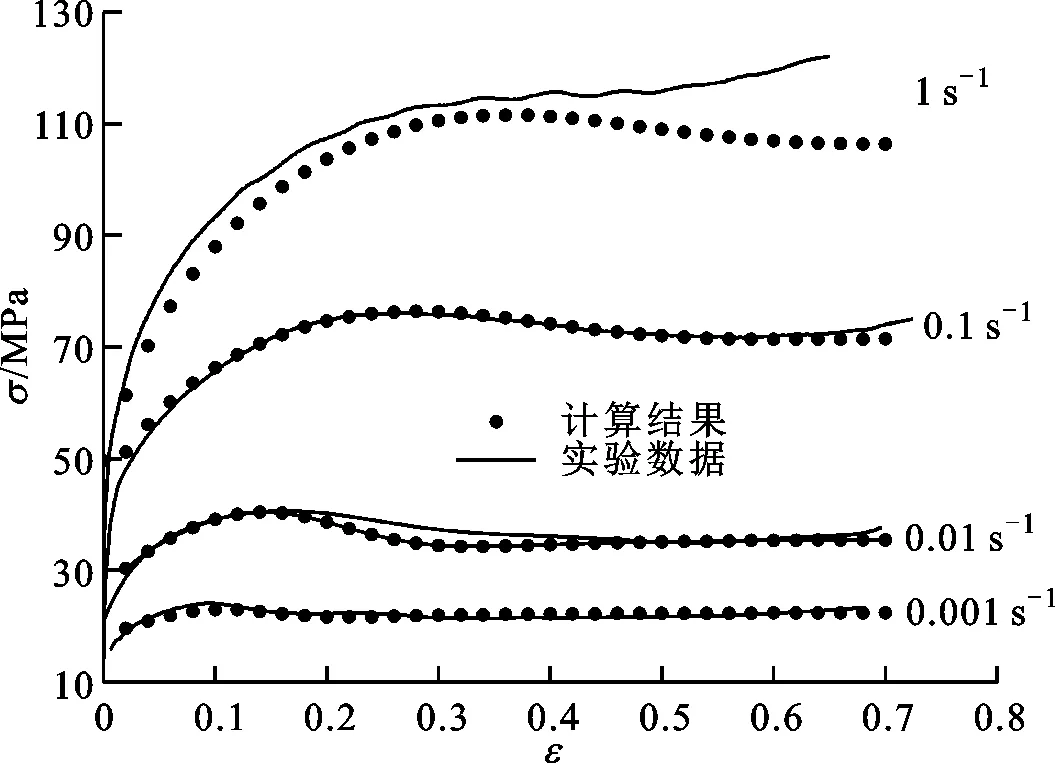
(a)T=1 200 ℃
(b)T=1 100 ℃
(c)T=1 000 ℃

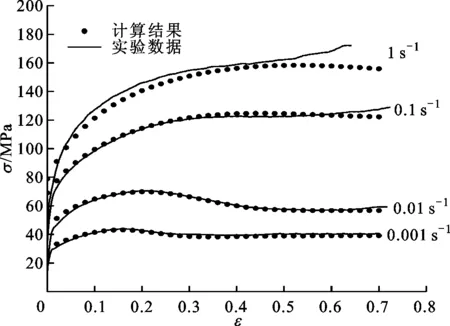
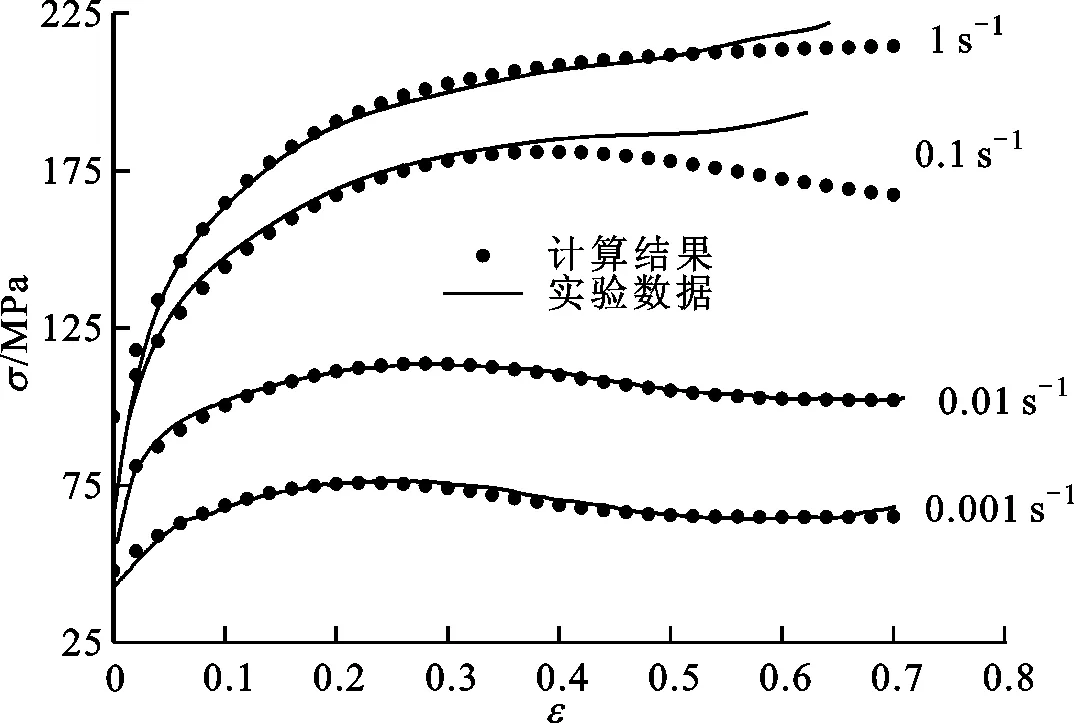
(d)T=900 ℃图11 控氮304不锈钢高温流动应力实验值与 模型计算值对比
2.3.4 流动应力模型验证 利用前面得到的控氮304不锈钢热变形流动应力模型对16组实验条件下的流动应力曲线进行预测,图11为预测结果与实验结果的对比,可见模型计算结果与实验结果吻合较好。其中应变速率为1.0 s-1及应变速率为0.1 s-1且变形温度为1 000 ℃或900 ℃时,在变形后期两者出现较大差别,其原因是在热压缩过程中,由于试样端部与砧子之间的摩擦使得圆柱形试样的不同区域变形不均匀。变形量较小时,这种不均匀性较小;变形量较大时,变形不均匀性增大,变形后期试样变为鼓形,导致所测得的流动应力偏高,出现流动应力曲线上翘的现象[18],特别是对应变速率较大、变形温度较低时,即Z较高时易出现这种情况[19]。以上原因使得应变速率较大、变形温度较低时理论预测结果与实验结果出现较大偏差。
2.4 组织演化动力学分析
图12给出了试样保温结束、变形之前的金相组织。图13给出了温度为1 200 ℃、不同应变速率下变形后的组织图。对比变形前的金相组织并结合流动应力曲线可以看出,这几种情况下均发生了完全再结晶;当变形温度一定时,应变速率越低,达到相同变形量时再结晶晶粒尺寸越大。图14为应变速率一定的条件下,不同变形温度得到的晶粒组织。可以看到,在900 ℃时,保留了较多伸长变形的原始晶粒,其晶界处有很多细小的动态再结晶晶粒,未发生完全动态再结晶,通过金相分析可知其再结晶分数为0.76;1 000 ℃时只残留少量原始晶粒,1 100 ℃以上均发生了完全再结晶,且温度越高,晶粒尺寸越大。

图12 试样变形前的金相组织




图13 温度为1 200 ℃时不同应变速率下的晶粒组织

(a)T=900 ℃

(b)T=1 000 ℃

(c)T=1 100 ℃

(d)T=1 200 ℃图14 应变速率0.01 s-1时不同温度下的晶粒组织
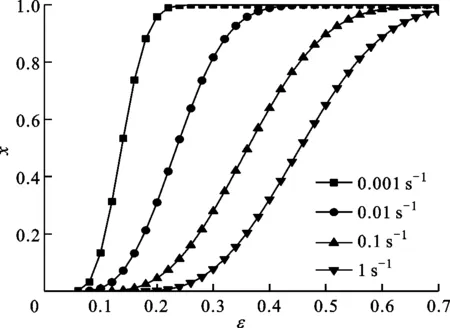
图15a为1 200 ℃、不同应变速率下的动态再结晶分数曲线,为典型的S型曲线。由图可见,应变速率为1.0 s-1时最终再结晶分数为0.98,其他应变速率条件下再结晶分数最终均达到1,表明都发生了完全再结晶;其次,应变速率越低,动力学过程越快,达到完全再结晶的应变越小,故而再结晶晶粒有较充分的时间长大,导致最终晶粒尺寸较大。图15b为应变速率0.01 s-1条件下,不同温度的动态再结晶分数曲线,由图可见,900 ℃时最终再结晶分数只有0.8左右,没有达到完全再结晶,与实验金相组织结果一致,但再结晶分数比金相分析结果(0.76)稍高,存在一定误差;1 000 ℃时最终再结晶分数为0.91,而1 100 ℃及1 200 ℃下均达到1,即发生了完全动态再结晶,也与金相组织一致;另外还可以看到,温度越高,动态再结晶动力学过程越快。
(a)T=1 200 ℃
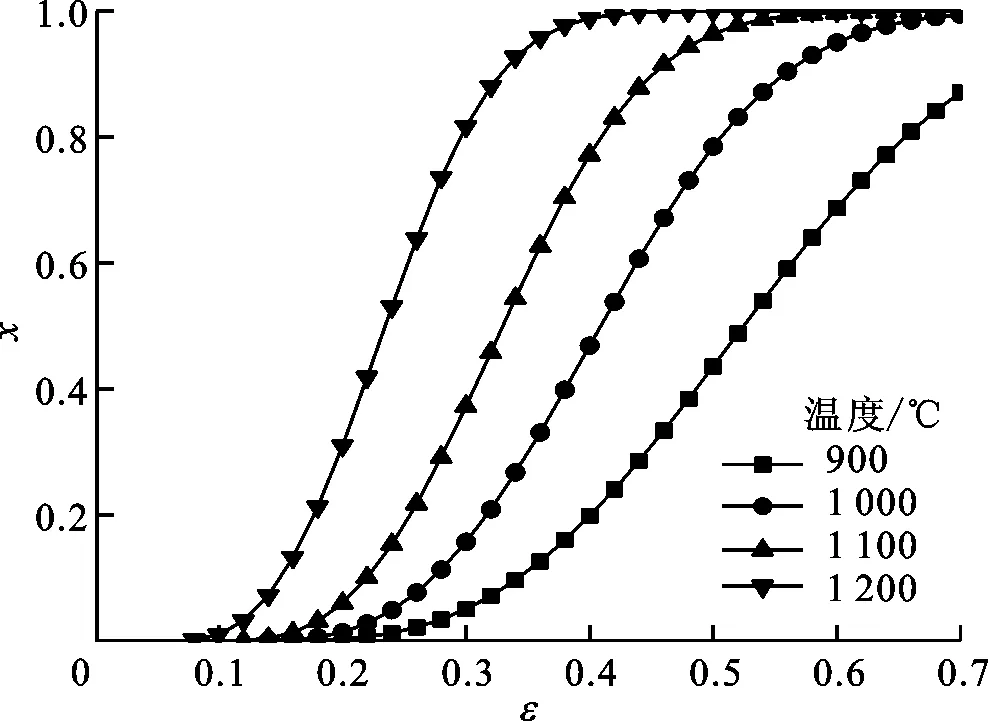
图15 不同条件下的再结晶分数曲线
3 结 论
通过热压缩实验对控氮304不锈钢在热变形程中的动态再结晶行为进行了研究,得到如下结果:
(1)变形温度一定时,应变速率越小,则流动应力越低,动态再结晶动力学过程越快,再结晶晶粒尺寸越大;而应变速率一定时,变形温度越高,则流动应力越低,动态再结晶动力学过程越快,再结晶晶粒尺寸越大。
(2)计算得到该材料的热变形激活能为385.755 kJ/mol,还得到了各特征参数及模型参数的拟合关系式,可以用于数值模拟。
(3)建立了该材料的热变形流动应力模型及动态再结晶动力学模型,流动应力模型预测的流动应力曲线与实验结果一致,动态再结晶动力学模型的计算结果与实验的组织演化结果一致。
