多级指标下的战场电磁环境复杂度评价研究

王帅，李婷

（陆军工程大学 石家庄校区装备模拟训练中心，石家庄 050003）

信息化条件下的战争中，电子设备和信息化武器装备得到广泛应用，战场上大量电磁信号交织叠加，动态多样，形成了复杂的战场电磁环境，对武器装备及其效能产生严重影响，成为未来战场争夺的焦点[1]。因此，对复杂电磁环境复杂度开展研究，认识电磁环境复杂度对作战训练的影响，发挥其在作战训练中的作用，对提高部队在信息化战场上的作战能力和训练效益具有重要意义[2-3]。目前，关于电磁信号产生的一般干扰环境对应的电磁环境复杂度的评估通常采用层次分析法或灰色评价方法等单一评价方法，误差往往较大，而采用集层次分析法、熵权法和灰色评价理论为一体的综合评价方法有助于充分消除人为因素，减少误差，从而得到客观评价结果。

1 评价方法理论

1.1 层次分析法

层次分析法适用于多目标决策复杂系统的评价，它将目标评价系统分解为多个目标或准则。这些目标或准则对应着目标评价系统的不同影响因素，形成递进式的多层次评价结构，按照层次分析法标度，给各影响因素赋值，进而构造判断矩阵。利用求解判断矩阵特征向量方法获得低层次各影响因素相对高层次准则的权重，将所得不同层次影响因素权重与具体量化值相结合，最终可得复杂系统评价的量化分析结果[4-5]。

在层次分析法的基础上，通过构造判断矩阵，并对判断矩阵进行归一化处理、一致性检验等，然后分别采用熵权法和“和法原理”对层次分析法中的综合权重进行计算和排序。由此，可得战场复杂电磁环境复杂度评价指标权重计算流程，如图1所示[6]。

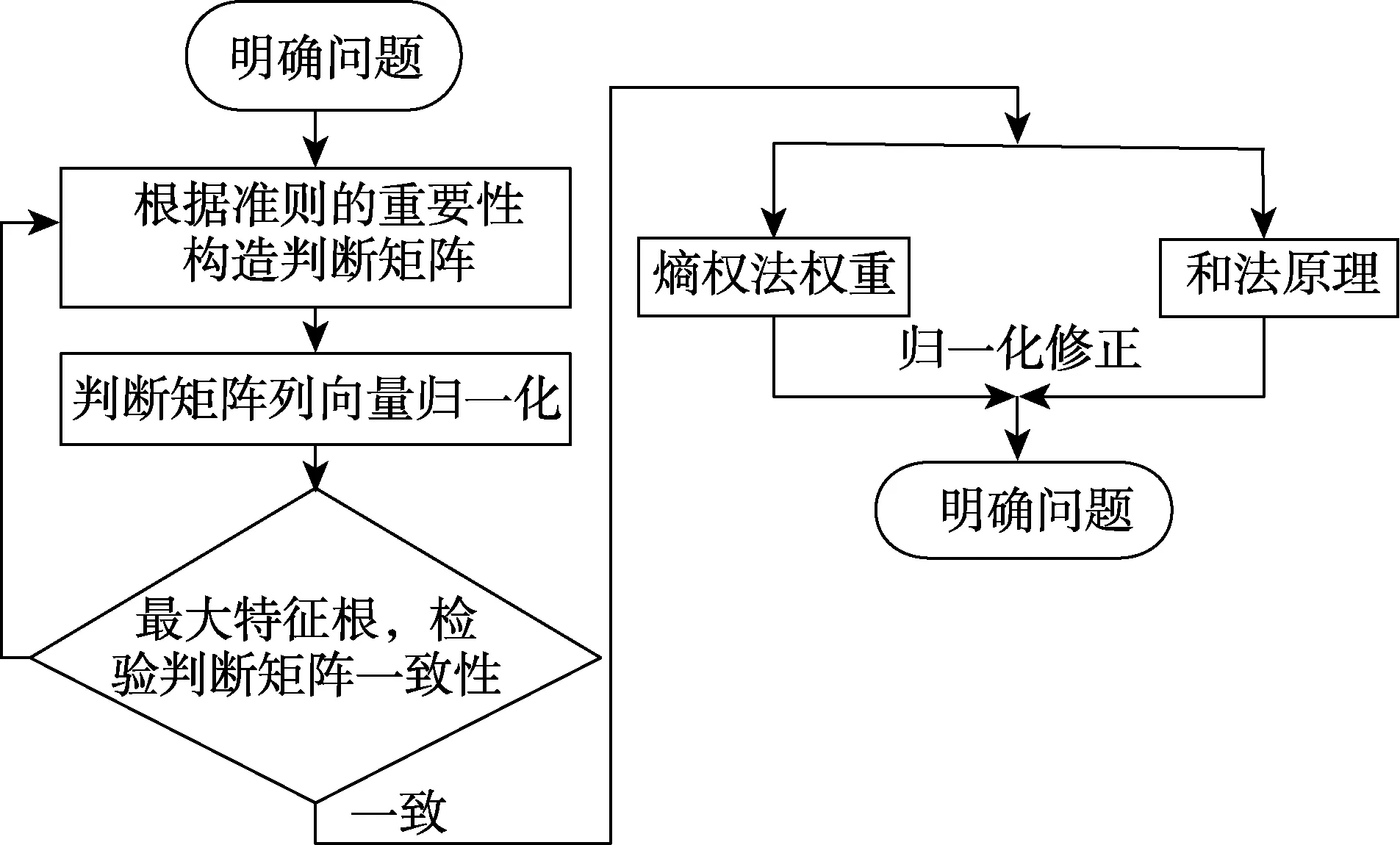
图1 战场复杂电磁环境复杂度评价指标权重计算流程 Fig.1 Evaluation process of complexity evaluation index weights of battlefield electromagnetic environment

1.2 和积法原理

层次分析法应用中需要求解各影响因素权重，由于层次分析法构建的判断矩阵属于正互反矩阵，其权重计算可以转换为权向量的计算，即要计算判断矩阵的最大特征根及其特征向量，归一化的特征向量即为权向量。权向量计算常用的方法包括“和积法”、“根法”以及“幂法”等，此处采用“和积法”计算权向量。

采用“和积法”计算权向量时，对于一致性判断矩阵，对其进行列向量归一化就是相应的权重；对于非一致性判断矩阵，对其列向量进行归一化再取其算术平均值作为权向量。为了对判断矩阵进行一致性判断，需要求取其最大特征根λmax，假定判断矩阵A的表达式为：

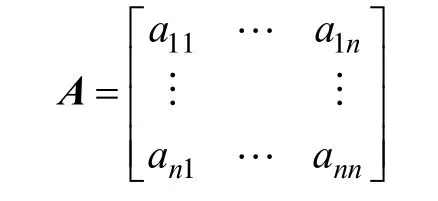
权向量W的计算过程如下：

1）将矩阵A的每一列向量归一化得：

2）对wij按行求和得：

3）归一化处理：

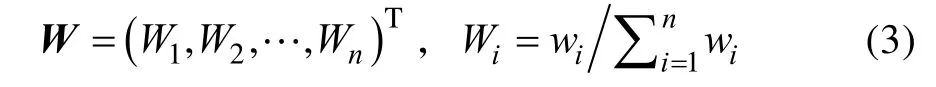
4）计算AW，则其最大特征根λmax值为：

1.3 熵权权重

层次分析法构造的判断矩阵过程中对指标赋值的主观性，导致判断矩阵可能会出现一致性、各指标权重相差过大等问题，因此文中采用熵权法来进一步计算综合权重，以保证权重的可靠性。熵权法建立在信息熵基础上，而信息熵来源于信息论，定义为随机变量的不确定性量度，用于衡量一个系统的有序程度，即一个系统有序程度越高，则熵就越小，所含信息量就越大。信息熵具有非负性、确定性、对称性、可加性。

以归一化后的判断矩阵R(rij)作为研究系统，H(i)为系统中第i个评价因素的熵值，按照信息熵定义可表示为：

式中：n为评价指标数；rij满足，且规定，当rij=0时，H(i)=0。

则第i个指标的熵权vi可表示为：

式中：m为指标个数。

同理，通过式（6）对其他评价指标进行解算，分别得出其对应的权重，最终可得基于熵权的评价指标权重向量[7]：V=(v1,v2,…,vn)。

1.4 评价指标综合权重

将“和积法”和熵权法分别计算所得的指标权重进行综合，然后对各综合指标进行归一化处理，便可得到修正后的各指标的综合权重。其综合计算和归一化处理过程计算公式为：

2 评价指标体系构建

电磁环境本质上是电磁辐射和辐射传播综合作用的结果，其中电磁辐射包括自然电磁辐射和人为电磁辐射，辐射传播是地理环境、电离层和气象环境等传播媒介对电磁辐射产生的作用。因此，评价电磁环境复杂度首要对电磁辐射以及电磁适应能力进行考察[8-9]。

在GJB 6520—2008《战场电磁环境分类与分级 方法》中，确定了一种对复杂电磁环境的分级方法。该电磁环境分级依据频谱占用度FO、时间占用度TO和空间覆盖率SO三个指标，通过计算总的频谱占用度、时间占有度、空间覆盖率及平均功率密度谱，综合确定战场电磁环境的复杂度等级。同时，由于平均功率密度谱AP描述了在一定的作战时间段、作战空间和作战用频范围内，电磁环境的平均功率密度谱的大小。环境电平门限So描述了电磁环境的功率密度谱对环境内工作的电子设备产生干扰的电平限值。因此，首先选取上述五个指标用于评价电磁辐射因素。

对于电磁适应能力的考察，选用电磁干扰度、电磁灵敏度和电磁稳定性[10-14]等三个评价指标。此外，由于复杂电磁环境包含大量的电磁信号源，存在各种形式的干扰，评价复杂电磁环境复杂度还需要考虑干扰因素。因此，选取了多径干扰、同频干扰和互调干扰等三种典型的干扰指标作为评价依据。文中考察的是一般意义上的电磁环境复杂度评价，评价过程中，上述评价指标值均通过专家打分法获取。综合以上评价指标，建立的战场电磁环境复杂度层次评价指标体系如图2所示。

图2 战场电磁环境复杂度评价指标体系与指标 Fig.2 Evaluation index system and index of complexity of battlefield electromagnetic environment

3 评价步骤

1）构造层次结构模型。按照第2节构建的评价层次与指标体系梳理评价层次结构模型，为构建判断矩阵做准备。

2）构造判断矩阵。引入一种标度用于各指标之间进行量化比较并得到判断矩阵，以“1—9标度”为例，指标i与指标j相互比较时，其中，1、3、5、7分表表示指标i与指标j同等重要、略微重要、明显重要、强烈重要、绝对重要，2、4、6、8为上述重要性的中间值。反之，指标i与指标j重要时，则取上述标度的倒数。

3）判断矩阵一致性检验与指标权重计算。采用和积法原理计算判断矩阵最大特征根和权向量，得到判断矩阵的特征向量和最大特征值分别为ω=[ω1, ω2,…,ωn]T和λmax。判断矩阵构造过程中，由于人的主观性存在偏差，需要对判断矩阵做一致性检验以提高权重计算的可靠性。首先计算一致性指标CI，其表达式为：

其次，利用层次分析法解决问题时，要对通过两两比较得出的判断矩阵进行一致性检验，而作为参与计算检验的平均随机一致性指标的值，一般需要查找Saaty计算好的1—8阶矩阵的RI值表进行比对。Saaty根据1000次正互反矩阵计算结果得到矩阵维数在1—8阶时对应的RI值，见表1。

表1 平均随机一致性指标RI表 Tab.1 Mean random consistency index RI table

然后计算一致性比例CR，其值为：

当CR<0.1时，判断矩阵满足一致性，此时在判断矩阵A归一化操作的基础上，结合信息熵、熵权以及和法原理进行各指标权重计算；当CR>0.1时，判断矩阵不满足一致性，要对判断矩阵做适当修正。最后采用熵权法计算指标权重，结合上面计算所得权向量，归一化处理得到指标综合权重。

4）确定评价指标矩阵。针对目标复杂系统，有n个专家对其中的m个指标进行评价，dij表示第j个专家对第i个指标的评价值，则可得目标复杂系统的评价矩阵为：

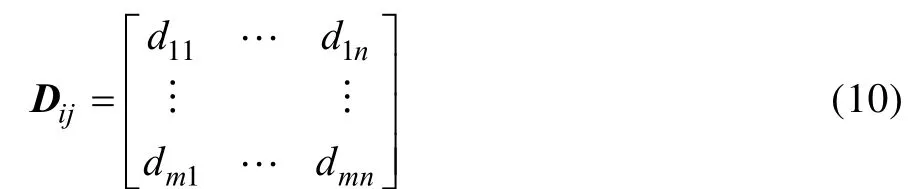
5）确定评价灰类。确定评价灰类，本质上就是要确定战场电磁环境复杂度的灰类评价等级数、灰数和白化权函数。评价灰类根据评价等级，定性分析确定。文中电磁环境复杂度对应4个评价灰类，分别是“重度”、“中度”、“轻度”、“洁净”，设定的评价等级集合为V={9,7,5,3}，则第一灰类“重度”，k=1，灰数为 ⊕∈ [9,∞)，其白化权函数为f1(dijk)；第二灰类“中度”，k=2，其灰数为 ⊕∈ [0,7,14]，其白化权函数为f2(dijk)；第三灰类，k=3，其灰数为 ⊕∈ [0,5,10]，白化权函数为 f3(dijk)；第四灰类，k=4，其灰数为⊕∈ [0,3,6]，其白化权函数为f4(dijk)[15]。f1(dijk)、f2(dijk)、f3(dijk)、f4(dijk)如式（11）所示。

上述评价灰类对应的白化权函数曲线如图3所示。

图3 白化权函数曲线图 Fig.3 Whitening weight function curve

6）计算灰色评价系数。对于评价指标i，电磁环境复杂度属于灰类k的评价权系数与总评价权系数为：

文中将复杂度分为4级，则第i个指标属于各个评价灰类的总灰色统计数hi值为：

7）计算灰色评价权向量和权矩阵。根据评价系数hik和hi，计算评价指标 的灰色评价权向量ri（ri=(hi1/hi, hi2/hi,…)），由此可得评价矩阵：

式中：q为指标数目；k为灰类数。

8）开展灰色综合评价。将各级指标权重与灰色权矩阵相乘，结合灰数将计算结果归一化，可得量化数值，确定最终结论[16-18]

4 战场电磁环境复杂度实例化评价

4.1 确定标度，构造判断矩阵

参照层次分析法常用的1—9标度法，确定准则层B层元素对目标层A、指标层C层元素对B层元素的标度，各元素之间的重要性标度见表2—4。

表2 准则（A）—电磁环境复杂度 Tab.2 Criterion (A)-Electromagnetic environment complexity

B1/B2 C1/C4 C2/C5 C3/C6 C1/C4 1 3 5 C2/C5 1/3 1 3 C3/C6 1/5 1/3 1

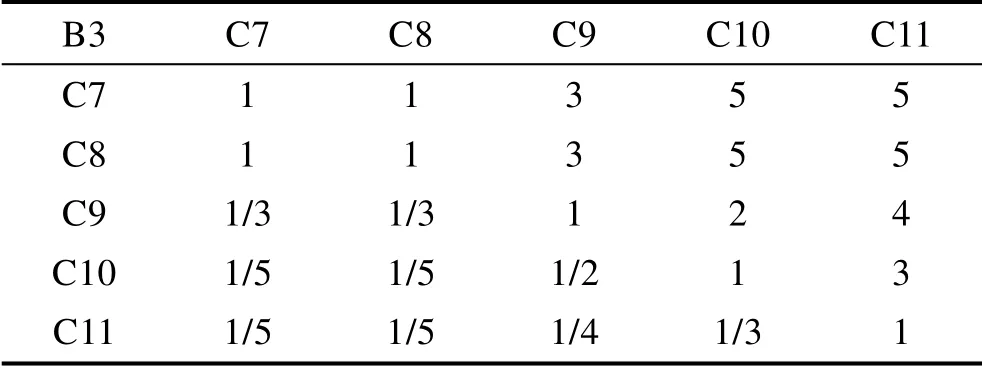
B3 C7 C8 C9 C10 C11 C7 1 1 3 5 5 C8 1 1 3 5 5 C9 1/3 1/3 1 2 4 C10 1/5 1/5 1/2 1 3 C11 1/5 1/5 1/4 1/3 1

由表2—4可得判断矩阵：

4.2 一致性检验，计算权向量

采用和法原理计算判断矩阵A1，A2，A3的权向量。以矩阵A3为例，首先将A3列向量归一化，可得：

对归一化矩阵按行求和得到：

对其进行归一化得到判断矩阵A3的权向量：

则最大特征根λmax3值为：

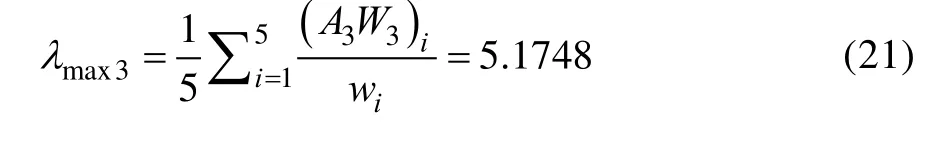
同理，也可得：

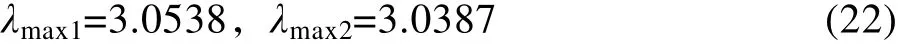
由式（8）可得矩阵A1，A2，A3的一致性指标CI分别为：0.0269、0.0194、0.0437。由此可得三个单排序的一致性比例值分别为：0.0517、0.0372、0.0390。CR值均小于0.1，表示每个判断矩阵的一致性都可以接受[19]。

在式（16）所示的归一化判断矩阵基础上，计算各评价指标的熵权值，由式（5）计算可得5个评价指标的熵值，见表5。得：

表5 判断矩阵归一化后熵值计算 Tab.5 Entropy calculation after normalization of judgment matrix

由式（6）可得5个指标的熵权权重：

由式（7）可得5个指标的综合权重： 同理可得：

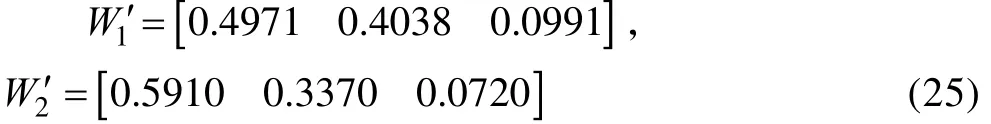
4.3 灰色综合评价

选定5名专家对11个评价指标进行打分，将电磁环境复杂度分为重度、中度、轻度、洁净4个等级，并分别赋值9、7、5、3，打分情况分别记为C31、C32、C33：

根据第3节和确定的四个灰类，结合对应的白化权函数，计算所得准则层的平均权矩阵，分别记为R(1)、R(2)、R(3)，结果为：

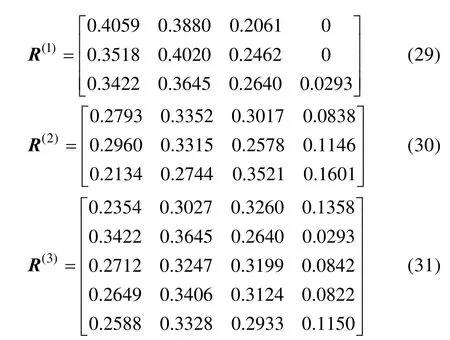
分别对准则层进行综合评价，以指标层B3为例，

其综合评价结果为：

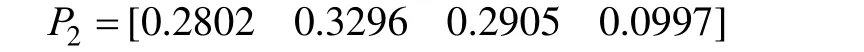
因此对目标层电磁环境复杂度综合评价值为：

各种评价灰类等级值化向量q={9,7,5,3}，结合目标层电磁环境复杂度综合评价结果[20]，可得目标层电磁环境复杂度评价值T6.9478 C P q= · = 。该结果介于灰数5和7之间，相应的电磁环境属于中度复杂。

5 结语

采用层次分析法和灰色评价法，选取了电磁干扰、电磁适应能力和电磁辐射三类共11项指标，对战场电磁环境复杂度评价过程与方法进行了研究。最后结合专家打分，得出了多指标下的战场电磁环境复杂度量化结果，实现了战场电磁环境复杂度评价。文中对战场电磁复杂度评价过程与方法具有一般适用性，然而本方法中的电磁环境复杂度划分主要适用于电磁信号产生的一般干扰环境，即广泛意义上的电磁干扰环境，而对于电子侦察装备的侦察环境及雷达、通信、导航等装备面临的特定干扰环境，还有待于深入研究。