基于短时傅里叶变换的飞行器故障振动信号分析

黄梦宏，朱令娴，张志勇，韩敬永，刘博

（1.中国运载火箭技术研究院，北京 100076；2.中国航天科工二院706所，北京 100854）

振动信号是飞行器飞行时的主要测量参数之一，主要用于检验飞行环境是否满足事先给定的环境试验条件要求，以及辨识飞行器的固有特性。在飞行器振动分析领域，一般采用基于傅里叶变换的加速度功率谱密度对振动信号进行分析，由于揭示了振动信号的频域特征，因此这种方法在国内外标准（如GJB 150.16A和MIL-STD-810F）中被广泛采用。但是这种方法存在一个无法避免的缺陷，就是只能给出一段信号整体的频域特征，而缺少时域定位功能，即对信号的表征要么完全在时域内，要么完全在频域内。对于平稳信号，由于信号的频域特征不随时间变化，因而功率谱方法可以很好地对其进行描述和分析。但是实际工作中测量到的振动信号，往往都是时变的或非平稳的，在这种情况下，只了解信号在时域或频域的特征是远远不够的，必须了解信号频谱随时间变化规律才能完整地掌握信号的特征。

为了解决上述问题，在处理时变或非平稳振动信号时必须采用时频分析方法。这种方法的基本思想是设计时间和频率的联合函数，用它同时描述信号在不同时间和频率的能量密度或强度。由于它能反映信号频率随时间变化的情况，因此非常适合处理非平稳信号。时频分析方法有很多种，如短时傅里叶变换（STFT）、Gabor展开、Wigner-Ville分布、小波分析和Hilbert-Huang变换等，其中短时傅里叶变换由于简单、易用，在国内外各工程领域得到了广泛应用[1-10]。

飞行过程中，飞行器上的振动信号是很复杂的，包括了气动噪声、发动机声腔振动和不稳定燃烧[11-12]等各种振动激励因素。其中气动噪声取决于飞行过程中不断变化的飞行姿态、动压等因素，发动机声腔振动和不稳定燃烧频率取决于随时间变化的发动机燃烧室声场特性。这些激励因素都是时变的，并且随着发动机工作，燃料不断减少，飞行器的固有特性也随时间发生变化，因此飞行过程中飞行器上的振动信号必然具有明显的非平稳特征。

当飞行器出现故障，其上振动信号的时频特性较正常飞行通常出现较为显著的变化，这为故障分析提供了一种新途径。文中基于短时傅里叶变换，对某飞行器飞行故障振动信号进行分析，通过对比正常振动信号和故障振动信号的时频特征，分析引起振动时频特性变化的各种因素，为飞行器故障分析提供依据。

1 短时傅里叶变换

短时傅里叶变换（STFT）又称为加窗傅里叶变换，是非平稳信号分析中使用最广泛的方法之一。这种方法将非平稳信号看作是由一系列短时平稳性信号构成，短时性通过在时域加窗来实现，通过平移参数来覆盖信号的整个时域。短时傅里叶变化采用一个窗函数与待分析的非平稳信号作乘积，实现窗口中心附近的开窗和平移，然后再进行傅里叶变换。

对于给定的非平稳信号s(t)，令h(t)是一个时间宽度很短的窗函数，它沿时间轴滑动，信号s(t)的短时傅里叶变换定义为：

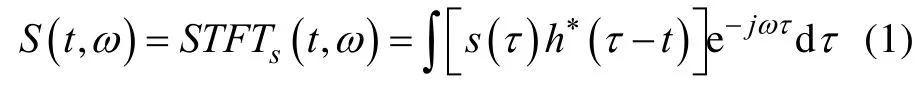
式中：*表示复数共轭。

从式（1）可以看出，信号s(t)在时刻τ的短时傅里叶变换，就是信号s(t)与一个以τ为中心的分析窗h*（τ - t）作乘积的傅里叶变换，分析窗 h*（τ - t）将信号s(t)在窗外的部分进行了有效的抑制，因此短时傅里叶变换是s(t)在分析时刻τ附近的局部谱，如图1所示。当分析窗函数h(t)=1， ∀t，即分析窗为全局的矩形窗时，短时傅里叶变换还原成传统傅里叶变换。

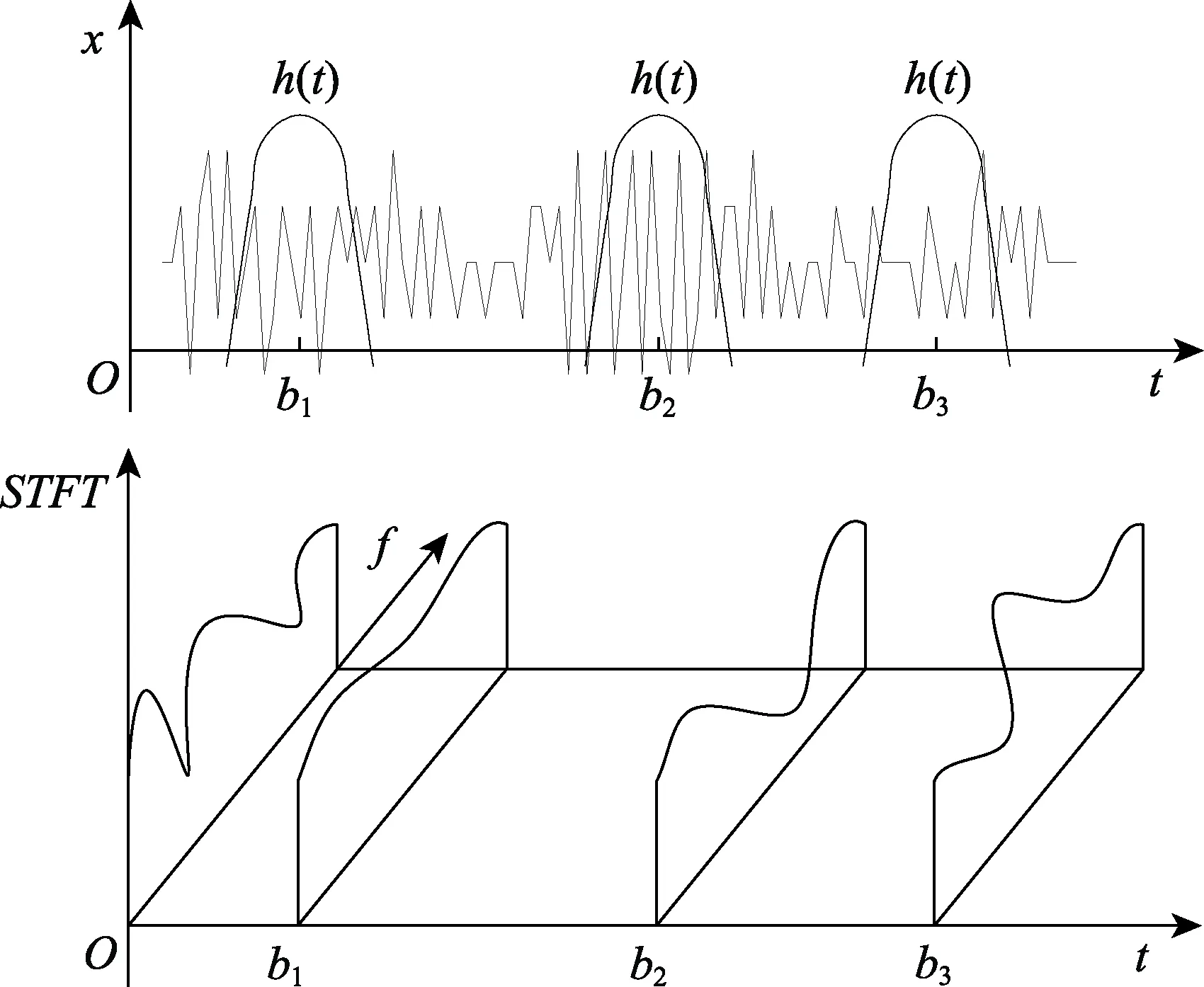
图1 短时傅里叶变换示意 Fig.1 STFT schematic diagram

在应用短时傅里叶变换对信号进行分析时，通常希望分析结果的时域和频域分辨率越高越好。但不确定原理表明，时域分辨率和频域分辨率不能同时任意地窄[13]，即时域和频域分辨率不能同时减小，其一方的减小必引起另一方的增大。因此对于给定信号，如何选择窗函数h(t)应视信号的频率特性而定。一般而言，对于高频信号，希望要有好的时间分辨率，以观察信号的高频部分（如冲击、尖脉冲等），即窗函数h(t)的时间宽度要小，此时对应的频率分辨率自然要下降。同理对于低频信号，则应降低其时间分辨率，以便在低频处获得较好的频率分辨率。此外，时间窗宽度的选取应确保在时间窗内的信号是局部平稳的，这是采用短时傅里叶变换处理实际信号的一个重要原则。

2 飞行器振动信号的短时傅里叶变换分析

以某飞行器飞行时的振动信号为研究对象，振动传感器安装于飞行器内壁，测量从飞行器起飞至发动机关机的振动数据。通常进行振动信号分析时，从测量信号中选取一段振动量级较大且近似平稳的数据作为分析样本。分析前采用滤波或消除趋势项等方法减少或消除信号中的长周期趋势项或高频噪声，使信号尽可能接近其真实值。两次飞行试验飞行器内壁同一位置的测量数据如图2所示，无论是否出现飞行故障，振动量级随时间均明显发生变化，振动信号具有明显的非平稳特性。从振动信号中可见，飞行器飞行中的各种物理现象，如发动机点火时的冲击，振动量级随飞行动压的变化规律等。此外，飞行器出现故障后的振动信号和正常飞行时的振动信号明显不同。正常振动信号在发动机点火之后，振动量级随时间先增大后减小，符合振动量级随动压变化的规律；但出现故障时的振动信号，在某个时刻点振动量级突然剧烈增大，没有反映出振动量级随动压变化的规律，与正常飞行时的振动信号差异较大。

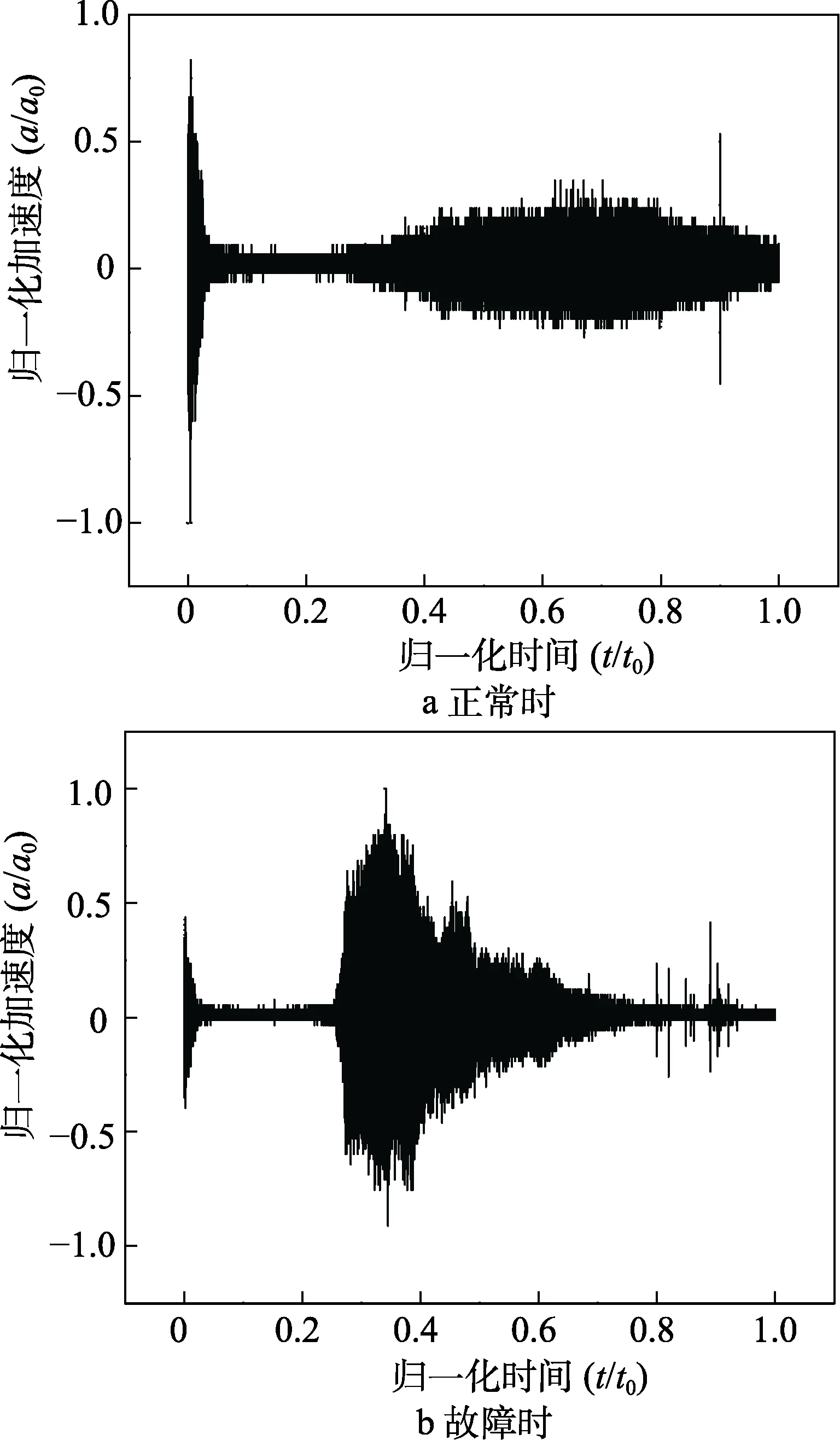
图2 飞行振动信号 Fig.2 Flight vibration signal: a) normal; b) in case of fault

2.1 短时傅里叶变换分析

在时间窗内信号平稳的原则下，对飞行振动信号时间历程进行了分析，确定了进行短时傅里叶变换的时间窗宽度以及对应的频率分辨率。故障振动信号和正常振动信号短时傅里叶变换谱如图3所示。正常振动信号表现的特征为飞行初期飞行器受外激励较小，各频段响应均较小；飞行中后期飞行器受外激励为高频段的宽频激励，各频段内的响应相差不大。故障振动信号在飞行初期的表现与正常振动信号相同，但在飞行中期出现某一频率及其倍频的突出响应，且这些响应的频率随时间逐渐增大，飞行后期这些倍频响应逐渐消失。可见飞行故障振动信号与正常振动信号主要不同在于飞行中期出现某一频率及其倍频的突出响应。

图3 短时傅里叶谱 Fig.3 STFT spectrum: a) fault vibration signal; b) normal vibration signal

根据故障振动信号的时频特征，结合可能引起这些特征的因素进行分析，可以对故障分析提供依据。由于振动传感器测量到的信号主要受三方面影响：一是各种激励，如气动噪声、发动机异常工作；二是飞行器固有特性；三是飞行器内设备工作或者电干扰。根据试验和计算获得的飞行过程中飞行器三方向的固有频率变化范围可以排除固有特性的影响。另一方面，由于气动噪声为高频段宽频激励，激励能量不会集中在某一频率及其倍频上，可以排除气动噪声的影响。此外，考虑到设备工作或者电干扰引起的频率在飞行器飞行中不会改变，可以排除设备工作或者电干扰引起故障信号时频特征的可能性。因此，在可能引起故障振动信号各种因素中，只有发动机异常工作因素不能排除，这一结论为故障定位提供了依据。

2.2 STFT与传统加速度功率谱对比分析

对飞行故障振动信号全程进行的加速度功率谱计算，结果如图4所示。对比图3a可见，采用加速度功率谱可以分析得到飞行中期出现的突出频率，这与短时傅里叶变化的结果一致。但加速度功率谱给不出上述频率成分的出现时间，以及随时间变化的关系，因此难以对故障定位提供支撑。

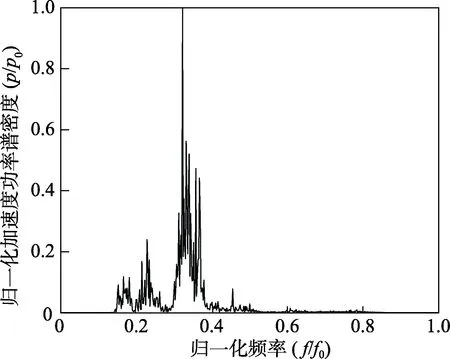
图4 故障振动信号加速度功率谱 Fig.4 Acceleration power spectrum of fault vibration signal

3 结语

飞行器飞行振动信号具有明显的非平稳特征，尤其是出现飞行故障时，其上振动信号的时频特性较正常飞行通常出现较为显著的变化，采用传统的基于傅里叶变换的加速度功率谱密度分析方法难以给出信号的完整特征。文中采用短时傅里叶变换方法对某飞行器出现故障时的振动信号进行了分析，克服了传统分析方法不能给出振动信号频率随时间变化关系的不足，给出了故障振动信号时频特征，为飞行故障分析提供了新途径。