基于MMD和AR-Kriging的160 t架桥机前起重小车车架结构优化
2021-03-08韩林山迟明刘耀唐明昊
韩林山 迟明 刘耀 唐明昊





摘 要:160 t全预制架桥机中的起重小车为直接受载部分,借助响应面代理模型对前起重小车的车架结构进行优化。使用相关性分析法和MMD算法选出具有代表性的样本点。通过AR-Kriging方法和多目标遗传算法对车架进行了优化。在对候选点进行验证比较后,确定了最终的优化结果,优化后车架的质量减轻了14.3%。
关键词:架桥机;相关性分析;MMD算法;AR-Kriging法;响应面优化
中图分类号:U445;TH122 文献标识码:A 文章编号:1003-5168(2021)36-0032-04
Structure Optimization of The Front Crane Trolley Frame of 160 t Bridge Erecting Machine Based on MMD and AR-Kriging
HAN Linshan CHI Ming LIU Yao TANG Minghao
(College of Mechanical, North China University of Water Resources and Electric Power, Zhengzhou Henan 450045)
Abstract:The lifting trolley in the 160 t fully prefabricated bridge erecting machine is the directly loaded part, and the frame structure of the front lifting trolley is optimized with the aid of the response surface proxy model. Use correlation analysis and MMD algorithm to select representative sample points. The frame is optimized by AR-Kriging method and multi-objective genetic algorithm. After verifying and comparing the candidate points, the final optimization result was determined. After optimization, the mass of the frame was reduced by 14.3%.
Keywords: bridge erecting machine; correlation analysis; MMD algorithm; AR-Kriging method; response surface optimization
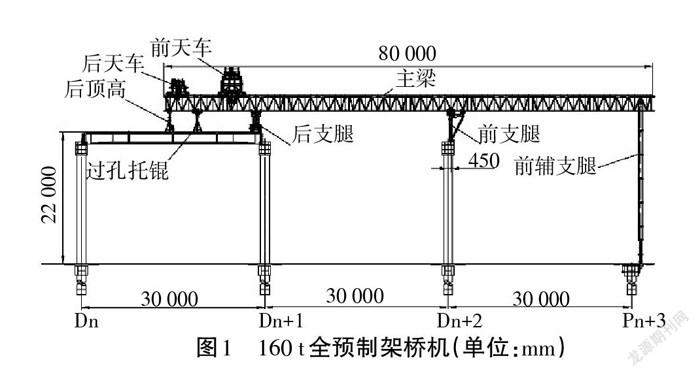
中國城市化进程以及桥梁建设技术的快速发展对桥梁施工的装备提出了更高的要求[1]。现提出一种新型的160 t架桥机,该型号的架桥机与双导梁架桥机的结构类似,包含支腿、主梁以及起重小车等结构,但该型号的架桥机采用提前预制完成的墩柱,在现场进行“拼装”的方式进行施工。为保证工作过程中架桥机的安全性,在架桥机中增加了前辅支腿的结构,这也是该型号架桥机在外形结构上的明显特征,如图1所示。
为了避免起重小车在吊运梁时出现吊具或梁体碰撞架桥机其他部分的问题,该型号的架桥机将起重小车置于一个可沿架桥机主梁移动的车架上。
起重小车是架桥机的直接受载部分,而其车架作为主要承载部分,车架的性能好坏会直接影响起重小车的工作状态,进而影响架桥机的工作性能。
响应面分析法是通过确定性试验来拟合一个响应面,进而模拟真实的状态,它是一种近似拟合方法[2-3]。构建响应面的方法有多种,如一阶响应面法、二阶响应面法、人工神经网络法等。在以上方法的基础上提出了Kriging方法,此方法可以对全局和局部的信息进行统计,同时,还可以预测样本的位置以及误差。研究人员结合Kriging法的主动学习和全局预测的特点,提出了一种可以自动迭代更新的自动优化Kriging方法——Auto-Refinement Kriging,简称为AR-Kriging[4]。为进一步提高准确度,使用了以MMD(Max-Min-Distance)算法为基础的空间填充试验方法来获取样本点[5-6]。
1 初始样本点的选取
1.1 确定设计变量
采用参数化建模的方式建立160 t全预制装配式架桥机前起重小车的车架模型,如图2所示。初选以下尺寸参数作为设计变量:[P1](主梁上板厚度)、[P2](主梁上板宽度)、[P3](主梁腹板厚度)、[P4](主梁腹板高度)、[P5](主梁腹板距离)、[P6](主梁下板厚度)、[P7](端梁上板厚度)、[P8](端梁腹板厚度)、[P9](连系梁上板厚度)、[P10](连系梁腹板厚度)、[P11](支腿直侧板厚度)、[P12](支腿斜侧板斜厚度)、[P13](支腿斜侧板直厚度)。
初始选定的设计变量为13组参数,由于这13组参数对车架性能的影响是不同的,因此,需要对这些设计变量进行筛选。通过筛选参数可以找到对计算结果影响显著的参数,即“抓住主要矛盾”;对初始选定的参数进行筛选后,可以在保证计算精度的同时,提高计算效率。
使用相关性矩阵对这些参数进行筛选,相关性矩阵图如图3所示,可以清晰地表示出各参数间的影响关系。
当相关性系数的绝对值小于0.2时,即可认为此组参数间没有相关性。依据这一判断准则,确定前起重小车车架的质量、等效应力、形变量,影响较大的设计变量为[P1]、[P3]、[P4]、[P5]、[P6]、[P11],对应的初始尺寸及变化范围如表1所示。
1.2 MMD算法生成样本点
在生成试验样本点过程中最主要的是要保证生成的样本点数量充足,即可以“充满”整个设计空间,且生成的样本点要具有代表性。
MMD算法可以根据整个设计空间中各设计点间的距离,将各设计点进行归类处理,选出最具有代表性的设计点作为样本点,故此方法属于一种聚类算法,其原理如下。
假设某一个设计空间为[D=x1,x2,x3,···,xn],在该设计空间中寻求最优的样本点的过程,即找出式(1)的解的过程。
[ZD=maxminxi,xjϵDxi-xj] (1)
式中:[xi-xj]表示设计空间中的设计点[xi]与设计点[xj]之间的欧氏距离。
将表1中经过筛选后的参数作为设计空间,并应用MMD算法,得到了具有良好代表性的样本点。对这些样本点的分布情况进行分析后,发现各样本点在设计空间中的分布情况较为均匀,说明这些样本点可以充分反映出设计空间的整体情况。
2 响应面模型的建立及验证
2.1 AR-Kriging响应面模型理论
Kriging响应面模型除了可以表示出已知的数据点,还可以对未知点进行预测,该模型对于未知点预测所采用的核心思想为:通过对已知的样本点与加权矩阵的乘积来对未知点进行预测。为实现以上目的,Kriging响应面模型由两个部分组成:一部分为确定性成分[hx],另一部分为随机过程[zx],它们与响应量[yx]间的关系表示为式(2)。
[yx=hx+zx=fTxβ+zx] (2)
式中:[fTx]为关于输入量[x]的基函数;[β]为该回归模型的系数矩阵;[zx]为均值等于0,方差是[σ2]的高斯随机过程。
根据已知输入量和对应的响应量的值,通过极大似然估计方法可以得到[β]和[σ2]的估计值,进而可以得到未知点的预测表达式为式(3)。
[yx=fTxβ+rxR-1Y-Nβ] (3)
式中,[R]是任意两个输入量间的高斯相关函数;[rx]表示未知点与输入量中已知点间的相关函数矩阵;[N]是包含[n]个元素为“1”的列向量。
AR-Kriging方法的原理为在Kriging模型建立的过程中,自动在全局误差最大的范围内插入设计点,之后采用梯度法对该区域中的设计点进行重新搜索,找出最优值,并将该值更新到已有的设计点中。
2.2 响应面模型的验证
使用较为直观的拟合优度图,对通过AR-Kriging方法建立的响应面模型的准确程度进行判断,拟合优度图如图4所示。
从图4中可以看出,通过该响应面模型预测的值与试验设计中的值基本保持一致。因此,可以断定该响应面模型具有较好的拟合优度,可以作为后续优化的响应面模型。
3 前起重小车车架的结构优化
3.1 建立车架优化数学模型
前起重小车在工作过程中始终在架桥机主梁的上方,其质量如果过大,会增加架桥机的工作负载。因此,将前起重小车车架的质量作为优化目标,将表1中的各参数作为设计变量。综上所述,得到了如下所示的优化数学模型:
[MX=min MP1 P3 P4 P5 P6 P11DX=max DP1 P3 P4 P5 P6 P11MX=max EP1 P3 P4 P5 P6 P11X=P1 P3 P4 P5 P6 P11TDX≤8 mmEX≤240 MPa]
式中,[M]為车架的质量,kg;[D]为车架的形变量,mm;[E]为车架所受的等效应力,MPa;设计变量[X]的取值范围已经在表1中给出。
3.2 优化结果及验证
选择优化算法为多目标遗传算法(MOGA),设定种群数量为2 000,最大迭代次数为20,分别设定变异系数和交叉系数为0.01和0.98,收敛稳定比设定为2%。对于设计变量,除了设置好其边界外,考虑到实际的加工方便,将搜索的步长设置为0.5。
考虑到使用代理模型进行优化时,会存在少许的误差。因此,设定三组候选点作为优化的最优解,然后从这三组候选点中进行筛选,经优化后得到的三组候选点以及相应的验证值如表2所示。
根据候选点的计算值和验证点的对比,发现偏差较小。这说明了使用该响应面模型进行优化分析的结果可靠度较高。通过表2发现,候选点1的最大形变量验证值为8.02 mm,超过了设定的形变量上限8 mm,故舍去。比较候选点2与候选点3,发现在满足约束条件的情况下,候选点3的形变量略大于候选点2,但是候选点3的最大等效应力值和质量都更小。因此,选定候选点3为最终优化结果,将前起重小车车架的原始参数和优化后的参数在表3中给出,可以看出经过优化后车架的质量减少了2 062 kg。
优化后的前起重小车的车架的形变云图以及等效应力云图分别如图5、图6所示。
4 结论
①本文将160 t全预制架桥机中前起重小车的车架作为优化对象,利用相关性分析以及MMD算法选择出了可以充分代表整个设计空间特性的样本点。
②通过拟合优度图对AR-Kriging方法建立的响应面代理模型的精度进行了判断,发现该响应面可以较为准确地反映出样本信息。
③根据已建立的响应面代理模型使用多目标遗传算法对车架的质量进行优化,对候选点进行验证后发现该方法的可靠性较高,通过比较各候选点的质量、形变量以及等效应力值确定出优化结果。
参考文献:
[1] 贾力锋.一种架设全预制桥梁架桥机的设计及应用研究[J].铁道建筑技术,2020(5):70-73.
[2] AELAEI M,KARIMIAN S,OMMI F.Sensitivity Analysis and Optimization of Delta Wing Design Parameters using CFD-Based ResponseSurface Method[J].Journal of Applied Fluid Mechanics,2019,12(6),1885-1903.
[3] 王欣欣,李中凯,刘等卓.基于响应面法的玻璃钻孔支撑结构优化设计[J].组合机床与自动化加工技术,2021(2):131-135.
[4] 秦强,赵朋飞,张文伟,等.基于自动改进Kriging方法的导弹舱体结构可靠性分析[J].导弹与航天运载技术,2020(6):16-22.
[5] 王美琪,李建.一种改进K-means聚类的近邻传播最大最小距离算法[J].计算机应用与软件,2021(7):240-245.
[6] 牟唯嫣,王春玲,赵昕.基于空间填充准则的交叉验证方法及其应用[J].系统科学与数学,2020(2):382-388.
