多元回归模型在基坑地下水位预测中的应用

陈建东

(广东省地质测绘院 ，广东 广州 510800)

随着城市化的飞快发展，人民对物质生活要求不断提高，各项土地资源开发越来越严重，特别在深基坑方面表现的尤为明显[1]。深基坑开挖施工复杂，技术风险大，对工程的地下水位预测提出了更高的要求[2-5]。通过国内外学者的不断研究，目前常用的地下水位预测模型有灰色系统模型、相关分析模型、回归分析模型等，灰色系统模型在数据波动较小的情况下预测精度较高，但是在波动较大时会产生较大的误差[6-10]。回归分析模型具有方程容易建立、使用方便等优点，本文利用常规回归模型对地下水位变幅进行预测，并以此为基础进行改进，加入起主要作用项的平方。

1 回归模型的建立

1.1 常规多元回归模型的建立

由于地下水受多个变形因子影响，利用多元回归模型更合乎实际。构建多元回归模型来拟合和预测[11-13]，其模型为：

yi=β0+β1x1i+β2x2i+…+βkxki+εi

(1)

式中，yi为y第i次的样本观测值;x1i,x2i,…,xki为对应yi的k个影响因子;β0,β1,…,βk为未知回归参数；εi为随机误差，εi～N(0,σ2)，且协方差σεi·εi-τ=0(τ≠0)。

所以误差方程为：

vi=β0+β1x1i+β2x2i+…+βkxki-yi

(2)

化为矩阵形式为：

V=Aβ-Y

(3)

式中，V=(v1,v2,…,vn)T，β=(β0,β1,…,βn)T，Y=(y1,y2,…,yn)T，

依据VTV=min ，得到法方程为：

(4)

从而得到参数的最小二乘解为：

(5)

最后得到多元回归方程为：

(6)

1.2 改进回归模型的建立

对于地下水的影响因素中，某一量起主要的决定作用，所以对常规回归模型进行改进，引入某一起主要作用量的平方，见式(7):

yi=β0+β1x1i+β2x2i+…+βkxki+βk+1xki2+εi

(7)

式中，xki为某一起主要作用的量。所以矩阵A为：

最后得到多元回归方程为：

2 工程概况

2.1 算例分析1

选取广州某基坑观测井GQ中观1孔，该井位于工厂广场副井西南侧，工程场地勘探范围内的土层划分为人工堆积层、第四纪新近沉积层、第四纪全新世冲洪积层、第四纪晚更新世冲洪积层四大类，地下水埋深在15 m左右。经过多年的动态观测分析，所选井的地下水位主要受大气降水、地表温度和地下水温度的影响。GQ中观1孔的观测数据如表1所示。

表1 GQ中观1孔观测数据

选取2019年8月25日～2019年12月20日观测数据作为模型的识别阶段，选取2019年2月25日～2019年7月25日观测数据作为模型验证阶段。故多元回归模型为：

yi=β0+β1x1i+β2x2i+β3x3i

(9)

式中，x1i,x2i,x3i分别为大气降水量、地表温度、地下水温度。

所以矩阵A为：

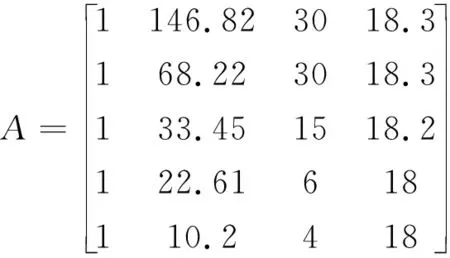
Y矩阵为：

所以可以得到回归模型为：

yi=-122.2+0.021x1i-0.097x2i+6.762x3i

(10)

利用此模型对GQ中观1孔观测井的2019年2月25日～2019年7月25日观测数据进行验证，将常规回归模型记为模型1。试验结果如表2所示。

由多年的观察可知，当地地下水变化幅度主要与降水量有关，所以把降水量作为主要影响因素，故改进多元回归模型为：

yi=β0+β1x1i+β2x2i+β3x3i+β4x1i2

(11)

式中,x1i,x2i,x3i分别为大气降水量、地表温度、地下水温度。

所以可以得到回归模型为：

yi=0.25-0.07x1i+0.109x2i-0.038x3i+0.001x1i2

(12)

利用改进模型对GQ中观1孔观测井的2019年2月25日～2019年7月25日观测数据进行验证，将改进回归模型记为模型2，与实测值、常规回归模型预测结果对比如表2所示，水位变幅绝对误差如表3所示。

表2 GQ中观1孔观测井的模型验证数据对比/m

表3 GQ中观1孔观测井的模型预测水位变幅绝对误差/m

由表3可知，常规回归模型水位变幅差值最大为2019年3月29日预测的，与实际水位变幅相差0.609 m，最小为2019年4月25日预测的，与实际水位变幅相差0.061 m，能达到预测的效果；改进回归模型水位变幅差值最大为2019年2月25日预测的，与实际水位变幅相差0.133 m，最小为2019年4月25日预测的，与实际水位变幅相差0.001 m，预测效果较好。

2.2 算例分析2

为了验证本文所提改进回归模型的有效性，采用另一组数据进行验证。选取广州某基坑观测井W3#水井，该井位于杨庄村以东农田内，工程场地勘探范围内的土层划分为人工堆积层、第四纪新近沉积层、第四纪全新世冲洪积层、第四纪晚更新世冲洪积层四大类，地下水埋深在3 m左右。经过多年的动态观测分析，所选井的地下水位主要受大气降水、地表温度和地下水的温度的影响。W3#水井的观测数据如表4所示。

表4 W3#水井观测数据

选取2019年3月29日～2019年6月25日观测数据作为模型的识别阶段，选取2019年7月25日～2019年11月30日观测数据作为模型验证阶段。故多元回归模型为：

yi=β0+β1x1i+β2x2i+β3x3i

(13)

式中，x1i,x2i,x3i分别为大气降水量、地表温度、地下水温度。

所以矩阵A为：

Y矩阵为：

所以可以得到回归模型为：

yi=-303.36-0.044 3x1i+0.134 39x2i+18.206 2x3i

(14)

利用此模型对W3#水井的2019年7月25日～2019年11月30日共5次观测数据进行验证，将常规回归模型记为模型1。试验结果如表5所示。

把降水量作为主要影响因素，故改进多元回归模型为：

yi=β0+β1x1i+β2x2i+β3x3i+β4x1i2

(15)

式中，x1i,x2i,x3i分别为大气降水量、地表温度、地下水温度。

所以可以得到回归模型为：

yi=0.25-0.07x1i+0.109x2i-0.038x3i+0.001x1i2

(16)

利用改进模型对W3#水井的2019年7月25日～2019年11月30日共5次观测数据进行验证，将改进回归模型记为模型2，与实测值、常规回归模型预测结果对比如表5所示，水位变幅绝对误差如表6所示。

表5 W3#水井的模型验证数据对比/m

表6 W3#水井的模型预测水位变幅绝对误差/m

由表6可知，常规回归模型水位变幅差值最大为2019年10月25日预测的，与实际水位变幅相差0.272 m，最小为2019年8月25日预测的，与实际水位变幅相差0.013 m，能达到预测的效果；改进回归模型水位变幅差值最大为2019年9月29日预测的，与实际水位变幅相差0.158 m，最小为2019年10月25日预测的，与实际水位变幅相差0.002 m，预测效果较好。验证了改进模型的有效性。

3 结 论

本文利用历史资料阐明了影响地下水水位幅度的影响因素，通过建立多元回归预测模型，初步对地下水位变化幅度进行预测，并以此为基础进行分析，发现降水量是影响地下水位变化的主要因素，提出了加入降水量的平方值的改进回归模型。通过两个实测数据，分别利用常规回归模型和改进回归模型进行对比分析，结果表明，改进回归模型预测效果更好，在实际应用中有参考价值。