基于层级控制的宏观基本图交通信号控制模型

王 鹏，李艳雯，杨 迪，杨华民

（长春理工大学计算机科学与技术学院，长春 130022）

（*通信作者电子邮箱ydi@cust.edu.cn）

0 引言

随着城市建设和社会经济的高速发展，城市道路拥堵现象越发严重。目前智能交通信号控制系统利用信号灯对路口交通进行调配疏导是缓解拥堵的重要方法之一。根据系统结构，城市交通信号控制可分为分布式和集中式控制，其中集中控制系统由中央计算单元控制，当控制范围扩大或参数增加时，整个系统的计算复杂度将呈指数增加，在信号优化过程中可能导致实时性与可靠性不能保持高度统一；分布式信号控制系统则不由中央计算单元控制，它依赖于局部交叉口控制器，不仅简化了模型结构，还可以保证信号优化控制的实时性与可靠性。

近年来，针对分布式交通信号控制优化问题，主要方法包括群体优化算法［1］、强化学习算法［2］、启发式动态规划算法［3］等。这些研究取得了不少的成果，然而交通信号控制优化通常是一个NP（Non-deterministic Polynomial complete）问题，这类交通控制方法计算相对耗时，易出现相位调节不及时等问题，难以保证在线交通配时决策的实时性。因此，在疏导拥堵的同时兼顾实时性在交通信号控制中就显得尤为重要。Wongpiromsarn 等［4］将分布式背压路由算法引入到交通控制领域，并首次提出了基于背压算法的分布式交通信号控制策略。相对于其他分布式算法，背压算法能够完全分布在交叉口上，只需要每个交叉口的局部信息，即可以用复杂度为O(1)的算法来实现信号控制。因此背压算法在交通信号优化方面受到了学者们的广泛关注，并在此基础上展开了大量的研究，提出了均衡下游路段剩余容量［5］、优化网络吞吐量［6］、考虑路段容量［7］等方面的改进。研究表明，城市道路交通系统具有分层多粒度特性，将系统中的交通元素粒化，以实现多角度、多层次解决问题。陈伟清等［8］将粗糙集与变异系数结合，建立了符合城市实际情况的智慧交通评价体系，为优化城市交通提供了有效的评价指标；Xie 等［9］基于粗糙集理论，将粒度计算引入智能交通系统，构建了交通数据挖掘模型；Abdel-Basset 等［10］提出了一个使用单值中性色和粗糙集理论处理不完全和不完全信息的一般框架，该模型提高了智能城市向其公民介绍服务和决策的质量。这些研究将粗糙集理论应用到城市交通优化中，取获得了不错的成果，也为城市交通信号控制提供了新的思路。Hao 等［11］利用基于S-粗糙集理论的基本转移操作，将每个交通粒用粗糙表示形式来表示，并对其动态特性进行描述，结合背压算法对区域内交通信号进行协调控制。

以上研究为交通控制方法提供了理论基础，然而，大多数研究在对城市交通信号控制进行分层多粒度优化描述时，只关注了针对不同粒度和不同层次交通元素的分布式优化控制策略，却忽视了对子区边界交通信号的控制，在区域交通信号的研究中，容易造成子区边界交叉口出现拥堵现象。如何建立合理的子区域边界交通信号控制模型，以实现区域边界交通疏导和整体路网的车流量最大化，成为目前的研究热点问题。宏观基本图（Macroscopic Fundamental Diagram，MFD）模型是目前研究较为广泛的区域边界信号控制方法。Yan 等［12］深入探讨了MFD 对信控参数的敏感性，并以此为基础提出了基于MFD 和遗传模拟退火算法的HGA（Hybrid Genetic simulated annealing Algorithm）模型；王力等［13］针对路网多子区协同控制考虑各子区拥堵状态差异性及均衡性的问题，提出了以多子区状态可达一致为目标的子区边界状态反馈控制设计方法；刘澜等［14］针对过饱和路网，提出了基于MFD 的可扩展边界控制策略，缓解了城市交通拥堵。以上研究表明MFD 综合路网间参数关系，能够反映城市路网的基本属性，并有效优化子区边界交叉口交通信号［15］。

综上所述，为进一步提升交通信号控制效果，本文针对子区域内部与子区域边界协调控制问题，提出了一种基于分层多粒度与MFD 的交通信号控制模型HMFD（Hierarchical multi-granularity with MFD），从交通元素状态的描述出发，引入S-粗糙集理论，采用分层多粒度的思想对研究路网内的交通元素进行描述；然后结合背压算法对子区内部交通信号控制，利用背压算法计算复杂度的特点，灵活应对不同车辆数的情况，保证交通信号控制的实时性；同时考虑子区间交叉口交通信号的优化控制，将区域驶出总流量最大和各子区内存在车辆数量最优为优化目标，利用MFD 建立边界信号控制双层优化模型。最后基于此构建整体模型框架，并对模型有效性进行了验证。

1 子区内交通信号协调控制

控制子区内的交叉口往往具有较高的关联度以及相似的交通状态，然而由于城市路网内的交通流具有随机波动的特点，控制子区内的交通状态是实时变化的，对交通状态的描述造成了一定的困难。因此为更好地描述交通状态，确保为控制交通信号提供及时、有效的数据，本章将利用S-粗糙集理论对子区内部元素进行描述，确定邻接路段上各交通粒子状态，以及各路段上的排队长度，并引入背压算法确定各交通信号的相位决策，达到子区内部的交通信号协调控制。

粗糙集理论由波兰学者Pawlak［16］首次提出，它可以根据论域U上的等价关系R确定其分类的对象集合。后来，Shi［17］指出粗糙集理论无法描述集合元素发生状态变化时的情况，并提出了S-粗糙集理论来描述集合的元素迁移情况。给定论域U，FUF′是定义在U上的元素迁移族，其中F=为U上的元素迁移元素，称X*⊂U是U上的双向奇异集合，其表示如下所示：

其中：f∈F，f′∈F′。X*的下近似表示如下所示：

X*的上近似表示如下所示：

对于不完全迁入和迁出的情况，上下附集表示如式（4）、（5）所示。其中，X为基于知识R可能确定分入的集合；u表示部分元素迁入X集合，x表示部分迁出X集合。

粗糙集理论是粒度计算理论的重要组成部分，它可以对系统中的元素进行粒化处理以实现多角度和多层次的解决问题。由车辆、车队、交叉口、路段、控制子区等组成的城市道路交通系统，也符合多粒度的特点；再者，交通系统也具有元素动态性，车辆的加速或减速，可能会导致其脱离或加入某一车队，信号灯不同的相位决策，可能会导致车队进入另一路段或子区。因此，本文将路网中的车辆、车队、交叉口、路段、控制子区划分为：车辆层（Vehicle Layer，VL）、车队层（Team Layer，TL）、路段&交叉口层（Section &intersection Layer，SiL）、控制子区层（Sub-area Layer，SL）四个层次，如图1所示。根据城市交通中路网的实际情况，将车辆定义为最小研究粒子，即车辆层，将在同一路段上具有邻接位置和速度相近的这些车辆定义为车队层，由于交叉口之间存在路段相连，将交叉口和路段看作一个整体，即路段&交叉口层，将研究路网中具有相近交通状态的路段&交叉口定义为控制子区层。

对应地，各层次中交通元素的粒子描述为车辆粒子（Vehicle Particle，VP）、车队粒子（Team Particle，TP）、路段交叉口粒子（Sections &intersection Particle，SiP）、控制子区粒（Sub-area Particle，SL），且有VP∈TP∈SiP∈SP，所以根据S-粗糙集理论为基础的TP、SiP、SP的双向奇异集合表示如下所示：

车辆粒子在不同层次上完全迁入的情况表示如下：

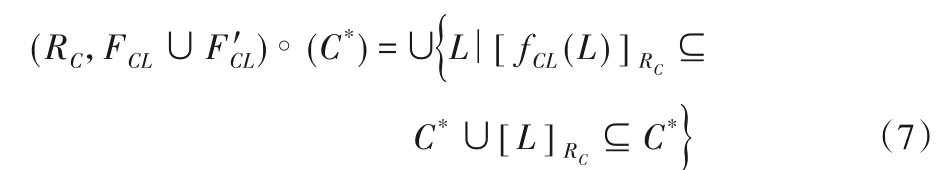
车辆粒子在不同层次上完全迁出的情况表示如下：

车辆粒子在不同层次上不完全迁入的情况表示如下：

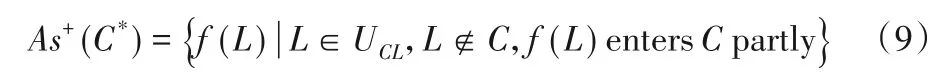
车辆粒子在不同层次上不完全迁出的情况表示如下：

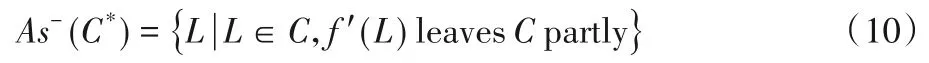
式（6）～（10）中C*可替换为TP、SiP或SP，对应地，L可替换 为VP、TP或SiP，CL为当前表示粒子所在层次，即TL、SiL、SL。F∪F′是定义在U上的元素迁移族，F={f1，f2，

图1 路网分层图Fig.1 Road network hierarchical graph

根据上文对交通元素的准确描述，有助于更准确、实时地获取路网中元素的状态和交叉口处的排队长度，为背压算法计算交叉口相位压力提供有效数据。背压算法首先被应用于无线数据包多跳网络的路由中，可以自适应地优化网络吞吐量并实现资源分配，在通信网络和无线传感器网络中得到了广泛的应用。本文也将背压算法引入到交叉口信号控制中，其基本思想是根据排队长度计算相位压力，选择最大压力相位激活，使对应车流获得通行权。针对交叉口各相位压力进行计算时，需要计算对应相位上下游路段压力，然后取其差值。将表示车队从a节点驶向b节点，wveh表示车辆在车队中的权重，a、β表示该车辆的压力权重系数。

针对子区内的交叉口相位压力的表示如式（14）所示，最后在相位切换时根据公式选择最大压力相位作为激活相位，使车流获得通行权，实现子区内网络的最大吞吐量。

2 区域边界协调策略

区域边界控制对于把控交通流的整体动向具有重要作用，而现有研究中往往集中在子区内部控制上，忽略了子区与子区间的边界信号控制，在实际应用中，这可能会导致车队进入另一子区的过程缓慢，造成子区边界交叉口出现拥堵现象，因此，本章将引入MFD 解决上述问题。MFD 是由Daganzo等［18］利用旧金山的路网数据推导出来的理论模型，研究表明MFD 作为路网区域内的固有属性，从宏观的角度来反映控制区域内的交通流性能，可以有效优化子区边界交通信号。MFD 可以表示整个区域内累计车辆数（Accumulation）和路网加权流量（Trip Completion Flow）之间的关系，有效反映子区间的车流的输出输入关系，如图2 所示。最大流量点的左侧表示未拥堵状态，右侧表示拥堵状态，随着车流量的增加，网络逐渐变得拥堵，它可以描述研究范围内网络的特征以及路网的交通动态。

图2 宏观基本图Fig.2 Macroscopic fundamental diagram

因此，将路网内的子区抽象成节点，形成简化的交通网络图，然后根据MFD 的特性，通过控制边界交叉口信号使研究路网处于最优状态，即驶出流量最大且稳定，路网内车辆数较多。将区域驶出总流量最大和各子区内存在车辆数量最优为优化目标，利用MFD建立边界信号控制双层优化模型。

上层模型以各子区输出车辆数最大为优化目标，研究路网的总输出车辆数-G，计算公式如式（15）所示：

其中：k为第k个研究时段；Gu(k)为子区u的输出流量与子区u内存在车辆数关系模型；Nu(k)为离散形势下各子区驶入驶出及存在车辆数的关系，计算公式如式（16）所示。

其中：N(0)为初始时刻路网内车辆数；Cj为交叉口信号周期（单位：s）；s为饱和流率（单位：veh/s）；gjh为第j个交叉口第h个进入路网车的流量的绿信比（指一个信号相位的有效绿灯时长与周期时长之比）为第j个交叉口第h个流出路网的车流的绿信比；J代表交叉口集合；H代表交叉口的进口道集合。

其中，Nuc为子区内达到阻塞密度对应的子区内存在的车辆数。

3 交通信号控制模型

基于以上研究，HDMF 结构框架如图3 所示。首先，利用城市交通系统的分层多粒度特性对交通要素进行描述；然后，根据分层多粒度描述给出的各粒度状态，采用背压算法计算各交叉口协同控制下的相位压力，实现城市路网区域的协同控制；最后，考虑子区域与子区域之间的流量输入输出关系，基于MFD 理论提出了边界信号控制策略，并建立了区域边界信号控制优化模型。

图3 HMFD模型结构框架Fig.3 Structure framework of HMFD model

算法的主要步骤如下：

步骤1 将研究区域中的网络划分为几个控制子区域，并将它们抽象为节点，子区间的连接道路抽象为有向线段，形成简化的交通网络图；然后根据宏观基本图的基本理论计算和记录子区间的流量输入输出及其关系G(N)。

步骤2 根据G(N)计算出子区的车辆输入量，并计算路段上车队排队长度L(k)。

步骤3 将排队长度L(k)代入式（14）中，可得出当前交叉口的相位压力；重复此计算过程，计算子区内各相位压力。

步骤4 在相位切换时根据公式选择最大压力相位作为激活相位，达到子区内网络的最大吞吐量。

步骤5 根据式（16）、（17）优化子区边界交叉口信号，实现在研究路网中，驶出总流量最大和各子区内存在车辆数量最优。

4 实验与分析

为了验证HDMF 模型的有效性，本章将通过Python 语言与SUMO 交通仿真软件在线交互，获取研究路网的实时交通状态，并将本文HDMF 模型与协同最大压力控制模型EMP（Extended cooperative Max-Pressure control）［11］和HGA 模型［12］进行对比分析。

利用SUMO 交通仿真软件构建实验路网，如图4 所示，参考了文献［19］中的谱聚类动态分区模型将路网划分成3 个子区，共包含23 个交叉路口。该路网包含19 个进出口，车辆输入量为2 000 veh/h；25个交叉口信号控制器，其中每个交叉口有4 个相位，包含东西直行相位、东西左转相位、南北直行相位，南北左转相位；每个路段上有3条车道，其中1车道上的车流为右转车流，该车流不受信号灯控制，2 车道上的车流为直行车流，3车道上的车流为左转车流，如图5所示，每个路口三个方向上的转弯率为33.33%；在各个交叉口设置检测器检测交叉口的交通数据，包括排队长度、驶离和驶入子区的车辆数量，检测器的数据采集周期为120 s。仿真时间为3 600 s，由于前1 000 s 车辆没有完全进入路网，容易对实验结果造成偏差，因此，对仿真结果的评价从1 000 s开始。

图4 仿真路网Fig.4 Simulated road network

图5 车道示意图Fig.5 Schematic diagram of lanes

图6 描绘了三种控制模型下的平均排队长度，该图显示在1 500 s 之前，HGA 模型的排队长度较低，随着时间的推移，由于HGA 模型的复杂度相对较高，计算耗时，导致在2 000 s后平均排队长度最高。EMP和HDMP的平均排队长度走势相对稳定，其中，HDMF 模型比EMP 模型、HGA 模型分别平均降低了6.35%和10.01%，得益于HDMF模型考虑了子区边界的交通信号控制，有效地进行子区边界交叉口疏导。实验果表明，HDMP可以有效降低平均排队长度。

图7 显示了三种模型的平均行程时间，HDMF 模型在一开始的平均行程时间并不比HGA 模型短，然而由于背压算法的复杂度较低，保证了在后期保持着稳定的平均行程时间，整体HDMP 模型的平均行程时间分别比EMP、HGA 模型降低了6.55%、11.15%。这表明HDMF 模型考虑子区边界的交通信号控制，可以有效提高车流量，使得区域内的车辆快速通过，防止在迁移到另一子区时造成拥堵现象；结合利用分层多粒度刻画的交通元素，可以更准确地描述其动态特征，及时提供有效的排队长度等数据，实现子区内交通信号相位决策。

图6 三个模型的平均排队长度对比Fig.6 Average queue length comparison of three models

图7 三个模型的平均行程时间对比Fig.7 Average travel time comparison of three models

子区内存在车辆数与驶离子区车辆数的关系如图8 所示，EMP 模型的驶离子区域车辆数随着子区内车辆数的增加而增加，然而子区内的车辆数超过子区路网的承受范围，会导致车辆无法驶出当前子区，整个路网趋于死锁状态，不利于整体路网的交通信号控制。HDMF 模型和HGA 模型符合MFD曲线，子区内车辆数维持在300 辆左右时，驶离子区的车辆数达到最多。

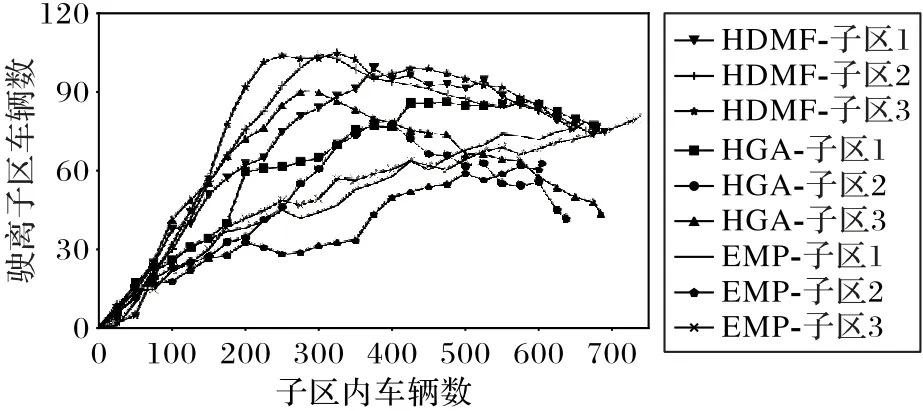
图8 子区内存在车辆数与驶离子区车辆数的关系Fig.8 Relationship between number of vehicles driving out of sub-areas and number of vehicles in sub-areas

表1 描述了三个模型仿真后驶离各子区的车辆数、离开率，以及离开研究区域的车辆总数。相较于其他两个模型，HDMF 模型驶离路网的车辆总数最多，而且每个子区都有较高的离开率，表明使用HDMF 模型能明显提高交叉口的通行能力，增加区域路网的交通流畅性，使控制区域内交通信号的效果更好，保证了整体区域交通量达到最大。

表1 三个模型中驶离各子区的车辆情况Tab.1 Vehicles driving out of sub-areas of three models

通过程序的运行时间来衡量模型的效率。实验路网如图4 所示，在各个交叉口设置检测器检测交叉口的交通数据，包括排队长度、驶离和驶入子区的车辆数量。输入车辆输入量分别为1 000、1 250、1 500、1 750、2 000，改变研究区域的输入车辆数，每个模型进行5次模拟，一共进行75次仿真模拟获得EMP 模型、HGA 模型、HDMF 模型的程序运行的时间结果如图9 所示。在仿真模拟后期时，会出现少量车辆驶出研究区域时间过长的情况，导致程序运行时间延长，为不影响整体实验结果及考虑区域内存在少量车辆具有现实意义，因此在驶离车辆达到一定数量时，不考虑区域内存在的车辆。在实验中发现，当驶离车辆数达到总车辆数的97.5%后，驶离车辆数增加非常缓慢，能忽略区域内剩余车辆，结束仿真模拟。

图9 效率图Fig.9 Efficiency chart

图9 显示了三个模型的运行效率，区域内车辆数有1 250辆时，HDMF模型与EMP模型的运行时间相差无几，从总体上看，在区域内车辆数在1 000 辆到2 000 辆之间，HDMF 模型的程序运行时间比HGA 模型和EMP 模型分别降低了2.05%和2.36%，具有较高的效率，这是因为HDMF 的计算复杂度低，能及时调节交叉口信号相位，同时考虑了边界交叉口交通信号的控制，保证了在线交通配时决策的实时性和流通性。

5 结语

本文基于S-粗糙集理论，利用分层多粒度的思想对交通要素描述，结合背压算法和宏观基本图理论，针对交通子区内部交通信号与子区间交通信号协调控制问题，提出了一种基于层级控制的宏观基本图交通信号控制模型HDMF。仿真实验的结果表明，该模型能够有效地减少交通拥堵，提高路网通行效率，保证区域内交通量最大化。由于条件限制，该模型测试对象和测试范围均有一定的局限性，下一步将探讨不同路网层次划分对交通信号控制的影响。