基于空间维度循环感知网络的密集人群计数模型

付倩慧，李庆奎，傅景楠，王 羽

（北京信息科技大学自动化学院，北京 100192）

（*通信作者电子邮箱sdlqk01@126.com）

0 引言

人群计数是智能视频监控系统的重要任务之一，目前对高密度人流的公共场所缺乏有效预警措施，易造成人群踩踏等隐患性事件。因此，分析人群行为趋向且对其安全隐患提供有效预警信息的人群计数系统对于建设智慧安全城市具有重要意义［1］。人群计数面临许多挑战，例如遮挡、高度混乱、人员分布不均匀、透视畸变、视角失真等问题。

通常人群计数方法是基于检测或回归。检测方法是通过对个体定位以给出计数［2-3］；回归方法是将人群作为整体研究对象，分析人群分布以建立特征与人数的映射关系，即通过人群特征与人数的映射关系给出计数。基于检测方法，何鹏等［2］利用KLT（Kanade-Lucas-Tomasi）跟踪器构建跟踪环节，基于多尺度块局部二进制模式（Multi-scale Block Local Binary Pattern，MBLBP）模型由对点跟踪转化为对人跟踪，实现了实时 计 数。Gao 等［3］在 卷 积 神 经 网 络（Convolutional Neural Network，CNN）的基础上结合级联Adaboost 算法作为特征提取器学习人群头部特征，通过对头部检测结果进行计数来获得人群数量。检测方法在人群个体独立且分布均匀的简单场景下能实现准确计数，但这需要目标具有清晰的轮廓特征。受监控设备的视角、距离以及场景中光照的影响，如图1 所示的大规模、高密度、宽视野的复杂场景，设感受野大小相等：S1=S2=S3=S4，设每个感受野中人数密度为δi(i=1，2，3，4)，由于透视畸变影响导致δ1＜δ2＜δ3＜δ4，即相同大小感受野中所捕捉到的人群数量随着景距的加大而增大，该现象对人群计数任务造成极大困难。

图1 高密度人群Fig.1 High-density crowd

随着近年来深度学习技术的飞速发展，目前国内外更趋向于采用基于CNN 密度回归方法实现计数任务。Zhang 等［4］提出了一种基于CNN 的跨场景人群计数框架，通过人群密度和人群计数两个相互关联的学习目标与数据驱动方法来捕捉人群纹理模型，提高了未知场景中人群计数准确率。Zhang等［5］提出了多列卷积神经网络（Multi-column CNN，MCNN），通过采用不同尺度卷积核的感受野来更充分地捕捉人群密度分布特征，在无透视矫正变换矩阵下能较为准确地生成密度图。在此基础上，Sam等［6］提出了基于图像中人群密度变化的切换卷积神经网络，利用多个CNN 回归器的固有结构和功能差异预测人群数量，通过执行差分训练机制来应对大规模和视角差异。Zhang 等［7］提出了尺度自适应网络结构，采用MCNN 提取特征，并在网络间增加自适应调整机制使之对特征的输出能够自主调节到同一尺寸以回归到人群密度图，在密度回归损失函数中加入基于人数的误差计算，密度图的回归精度随即提高。近年来，深度卷积神经网络在多个计算机视觉研究主题中取得了成功，Pu 等［8］提出了基于深层深度卷积神经网络的人群密度估计方法，即引入GoogleNet 和VGGNet 实现跨场景人群密度估计。随着CNN 深度的不断增加，其参数量与网络结构也随之增加，网络训练变得困难，准确度未有效提升。为了进一步消除透视畸变、视角失真导致比例变化对计数准确率的影响，郭继昌等［9］提出了基于CNN 与密度分布特征的人数统计方法，将人群图像依据密度进行划分：高密度图像的透视畸变问题使用多核回归函数处理；稀疏图像中个体分布较均匀，即对场景去噪后基于个体位置研判人群数量。Xu等［10］提出了深度信息引导人群计数方法，即基于图像深度信息将其划分为远景与近景，远景区域基于MCNN 回归人群密度图，近景区域基于YOLO 框架检测人群数量，并结合空间上下结构消除误差。Ma 等［11］提出了原子卷积空间金字塔网络（Atrous Convolutions Spatial Pyramid Network，ACSPNet），采用递增的原子速率排序的原子卷积核增大感受野并保持提取特征的分辨率，空间金字塔中使用无规则卷积进行多尺度感知且连接集成多尺度语义。陆金刚等［12］提出了基于多尺度的多列卷积神经网络（Multi-scale MCNN，MsMCNN）的计数模型，引入了多尺度连接以结合不同卷积层的特征学习视角和尺度的变化。马皓等［13］提出了特征金字塔网络人群计数算法，结合高级语义特征和低层特征以多尺度特征回归密度图。郭瑞琴等［14］提出了GB-MSCNet（Gradient Boosting Multi-Scale Counting Net）人群计数网络，该结构增大了网络输出层感知野以保存细粒度信息，同时将多尺度特征融合生成更准确的密度图。Zhu 等［15］提出了层次密度估计器和辅助计数分类器，引入了软注意力机制，基于分级策略从粗到精挖掘语义特征以解决缩放比例变化和视角失真的问题。Wang 等［16］提出了基于通道和空间注意力机制的人群计数网络，分别从通道和空间维度自适应地选择不同接受场［17］的特征，适当获取空间上下文信息。

随着研究的不断深入，上述文献中的方法对于计数的准确率已取得不错的效果；但是局限于密度区域的划分［9-10］，仍需要大量的计算成本来确定区域边界和削弱前景对象之间的上下语义依存关系，导致模型在复杂场景中的性能下降；或因为引入多尺度感受野的卷积层［11-14］，增加了模型复杂度且未考虑到图像视角旋转变化，一定程度上限制了模型对视角变化的鲁棒性。因此，受文献［18］的启发，本文提出了一种应用于空间维度上循环感知的人群计数模型LMCNN。本文的主要工作如下：

1）引入空间维度上局部特征循环感知网络，基于长短期记忆（Long Short-Term Memory，LSTM）单元的顺序编码对图像区域之间的全局空间上下依存关系进行存储，进一步在局部区域学习透视畸变、视角失真的高密度人群内部透视变化信息；

2）设计端到端特征图分割机制，将主干网络的特征输出自发地进行序列化，从而实现不同维度的特征空间的转换。

1 高密度人群计数模型

如图2 所示，本文提出了一种应用于空间维度上循环感知的高密度人群计数模型，由全局特征感知网络（Global Feature Perception Network，GFPNet）和局部关联性特征感知网络（Local Association Feature Perception Network，LAFPNet）两部分组成。为了进一步提高密集人群计数准确性，改善图像透视畸变、视角失真问题，先由GFPNet 有效提取人群图像分布特征，再由LAFPNet 循环感知特征图序列化的内部空间维度，以进一步在空间维度上迭代提取深层语义特征，最终计算残差值以优化人群图像密度。

1.1 GFPNet

GFPNet 将输入图像经处理后转换为低维特征图，提取深层语义特征。受Zhang等［5］工作的启发，设计了多尺度工作模式的GFPNet（如图3 所示），基于不同尺度的卷积核对图像中不同密度的人群空间分布特征进行提取，即不同尺度的感受野提取不同比例的图像特征。由于透视畸变等问题导致卷积核提取特征的局限性，通过LAFPNet 基于全局上下相关性以进一步细化密集区域图像特征。如图3 所示，GFPNet 由三列并行的神经网络组成，每列共有5 层不同尺寸卷积核和通道数的卷积层，以及两层最大池化层，在Conv 层参数s×k×k×N中，s表示卷积核步长，k×k表示卷积核尺寸，N表示卷积核通道数；MaxPooling 层参数2 × 2 表示为池化区域且池化步长为2。

三列子卷积神经网络中Conv_5 层输出的特征图经Concat相连接，并且经Conv_6层中卷积核尺寸为1× 1且通道数为1 的卷积层感知后生成特征图。经两层最大池化处理，其生成特征图的分辨率为输入图像的1/4，大大降低了网络的参数量和耦合度，减少了优化工作量。

图2 LMCNN模型结构Fig.2 Structure of LMCNN model

图3 全局特征感知网络结构Fig.3 Structure of global feature perception network

1.2 LAFPNet

LAFPNet优化人群密度特征图，提出基于LSTM 单元的顺序编码存储区域之间的全局空间上下依存关系，该网络主要由空间变换网络［19］、LSTM单元和残差优化组成。

其中TD为空间位置变换，基于其空间不变性特点，从GFPNet 输出特征图中突出局部高密度区域，如式（1）所示。为保证LAFPNet 能输入任意尺寸特征图，引入了空间金字塔池化层（Spatial Pyramid Pooling Network，SPPNet）［20］，避免因不满足输入尺寸要求对特征图进行缩放造成失真等问题。根据SPPNet 理论，基于网络高度对其特征进行提取，每层金字塔网络的感受野为2m× 2m(m=0，1，…，n-1)，考虑到GFPNet 中有五层卷积层，将金字塔层数设为5。受限于Caffe中LSTM 单元输入要求为一维向量，Slice 层在特征图的垂直维度上进行分割，将特征图按照其高度均等分割成16 份，分别为LSTM单元16个时间步输入。

其中θij为将特征图进行平移、旋转、裁剪等运算的变化参数。

1.2.1 LSTM单元

如图4 所示，LSTM 单元对一段连续型特征具有较强的记忆性，能够记忆历史特征信息，每个时刻提取的特征都会对下一时刻提取的特征产生影响。因此，LSTM单元能够感知局部高密度区域空间位置中上下特征的相互依存关系，从而使局部区域人群分布特征的感知更为细化，减弱图像畸变、视角失真对于人群计数的影响。该“记忆性”特点由遗忘门、输入门、输出门三个门控单元控制。遗忘门ft控制之前特征信息对当前的影响，其输入为前一时刻的输出ht-1和当前时刻的输入xt；输入门it控制信息流的更新；输出门ot控制网络信息的流出，分别如下所示：

ct表示当前的记忆状态，遗忘门和输入门对其进行更新，其中为当前时刻记忆单元的更新值，公式为：

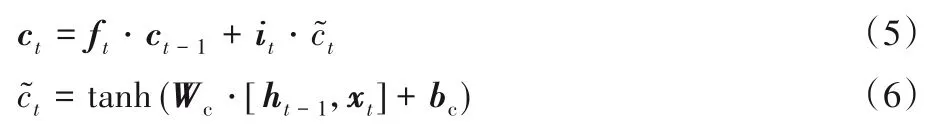
特征信息经提取后，最终输出状态值ht表示为：

其中：Wf、Wi、Wo、Wc为权重矩阵，bf、bi、bo、bc为偏置项。

上述公式详细介绍了LSTM 单元工作原理。单元细胞基于时间顺序连接，每个时刻提取的特征会对后续提取特征提供信息，不同时刻的特征相互影响，增强后续特征提取的可靠性。

图4 t时刻的LSTM单元结构Fig.4 Structure of LSTM cell at time t

1.2.2 残差优化

基于密度图回归的方法通常采用随机梯度下降法进行网络优化，以欧氏距离函数进行损失计算，进一步优化结构参数，损失函数定义如下：

其中：N代表训练样本的总数；Ii代表第i张训练图像Xi对应的真实密度图；I(Xi；Θ)代表训练输出的密度图，Θ代表需要学习的参数；L(Θ)是训练输出的密度图与真实密度图之间的差距。

1.3 人群密度图

当图像中人群稀疏并且图像中人头尺寸具有一致性时，采用传统高斯核函数方法生成密度图。即假设某个人头中心点在像素xi上，该密度用狄拉克函数来近似表示为δ(x-xi)。高斯核滤波器为Gσ(x)，人群密度函数为：

在高密度人群图像中，人群个体间并非相互独立，由于透视畸变问题，人头在图像中不同区域的尺度不同，则采用自适应高斯滤波器Gσi(x)［12］计算人群密度函数：

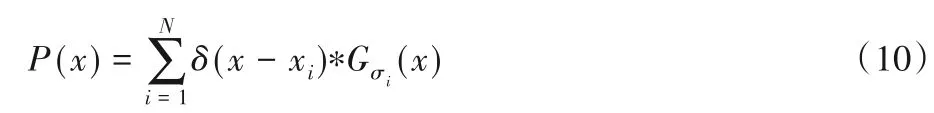
2 实验与分析

为更加充分地验证本文模型的有效性，基于Shanghaitech数据集和UCF_CC_50 数据集进行训练与测试，并与经典、主流的人群计数算法MCNN［5］、ACSPNet［11］、GB-MSCNet［14］进行对比。本文实验环境基于Linux 系统，使用Caffe 作为训练框架，程序语言为python 3.5。

2.1 数据集

人群计数任务对数据集的要求一般包括两个方面：不同疏密程度的人群图像以及相对应的人头中心点像素坐标的标签文件。目前人群计数研究所使用的主流开源数据集有Shanghaitech、WorldExpo’10、UCF_CC_50、UCSD 等，本文实验结果主要基于Shanghaitech、UCF_CC_50 数据集，其详细信息如表1所示。

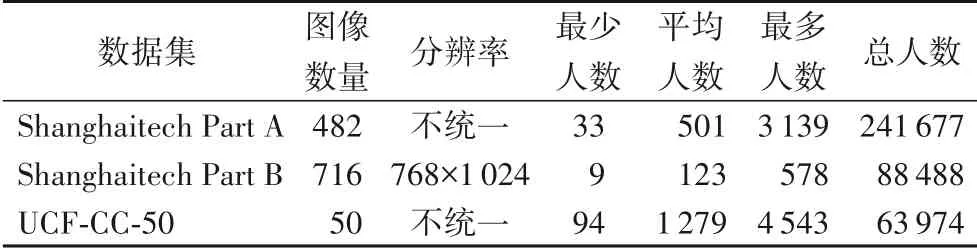
表1 Shanghaitech和UCF_CC_50数据集信息Tab.1 Information of Shanghaitech and UCF_CC_50 datasets

1）Shanghaitech数据集。

Shanghaitech 数据集是由Zhang 等［5］提出的具有多尺度疏密人群分布特点的大型数据集，该数据集包含两部分：Part_A和Part_B。Part_A 是从互联网上随机爬取的482 张不同场景高密度人群图像，包含300 张训练图像和182 张测试图像；Part_B 是从上海市繁华区域采集的716 张中小密度人群图像，包含400 张训练图像和316 张测试图像，是目前使用最多的人群计数数据集。

2）UCF_CC_50数据集。

UCF_CC_50共有50张人群图像，每张图像的人群总数在94到4 543之间，密度分布差异较大。该数据集数据量较少且人群密度较大，对网络计数准确率挑战极大。

考虑到人群图像的样本量过少，容易导致过拟合现象，因此在数据预处理阶段进行数据增强，主要通过裁剪操作以扩充样本，最后将所有图像按照8∶1∶1 随机划分成训练集、验证集和测试集。

2.2 评价指标

网络评价指标采用平均绝对误差（Mean Absolute Error，MAE）与均方误差（Mean Square Error，MSE），MAE 反映了网络的预测精度，MSE反映了网络的泛化能力。计算公式如下：

其中：N为测试集的人群总数，ni为第i张测试图像的真实人群总数，ni为第i张测试图像的网络预测人群总数。

2.3 LMCNN计数性能实例验证

将该模型与文献［5，11，14］算法进行对比，其中文献［5］注意到CNN 中卷积核尺寸固定，同一卷积核卷积运算的感受野大小不变，未考虑透视畸变对于人群密度分布的影响，率先提出MCNN 结构，采用多列卷积与不同尺寸卷积核学习密度分布特征，是人群计数领域经典模型；文献［11］在此基础上进一步采用按原子速率排序的原子卷积结构、金字塔结构的无规则卷积块跳过连接方式和权值与功能共享，在保证分辨率的同时扩大感知范围以集成多尺度特征；文献［14］基于优化Inception-ResNet-A 模块和Gradient Boosting 集成学习方法设计端到端的网络结构，采用较大的感受野以融合多个尺度的特征，是目前评价指标较好的模型。

2.3.1 基于Shanghaitech数据集的实验结果

在数据预处理阶段，如图5、6 中（a）所示，将图像随机裁剪相同大小的4份，同时保证这4份子图相互叠加能够覆盖整张图像。在Shanghaitech数据集上，对Part_A与Part_B分别进行了训练与测试，不同算法的实验结果如表2所示。

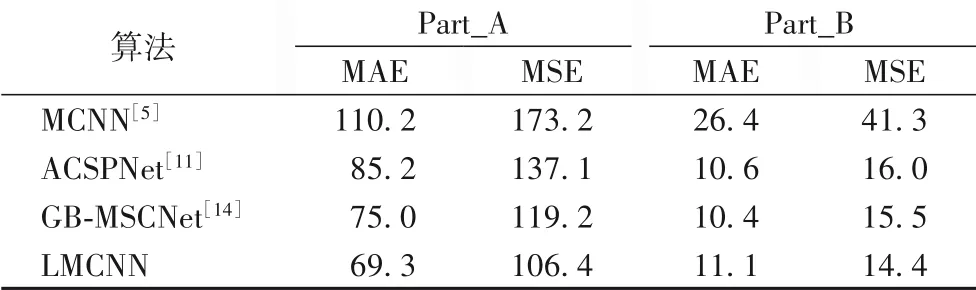
表2 不同算法在Shanghaitech数据集上的MAE和MSE对比Tab.2 Comparison of MAE and MSE for different algorithms on Shanghaitech dataset

由表2 来看，LMCNN 模型在稠密度较高的子集Part_A 上表现优于其他方法，它的MAE 与MSE与经典算法MCNN 相比显著减少，相比基于CNN 结构的ACSPNet 算法分别减小了18.7%和22.3%，相比目前较好的算法GB-MSCNet 分别减小了7.6%和10.7%，说明LAFPNet充分学习到了高密度区域特征；但在如图6（a）所示稠密度较低的子集Part_B 中，LMCNN的MAE 表现略逊于GB-MSCNet，Part_B 为低密度图像，背景主要为街道且布局杂乱，LAFPNet 过多提取背景特征，导致MAE 稍大。图5 与图6 分别展示了模型在数据集Part_A 与Part_B 随机图像的真实密度图与预测密度图的对比，充分说明网络预测密度图较为准确地反映了图像真实密度。

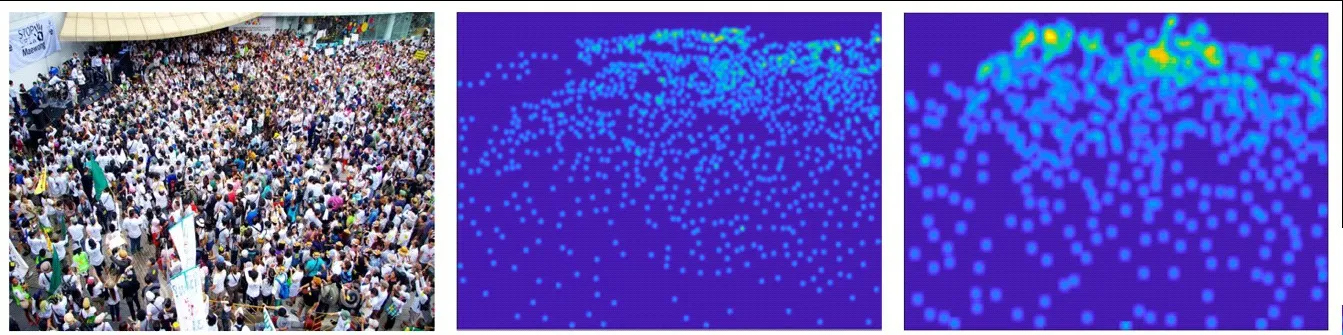
图5 Part_A测试图像的真实密度图与预测密度图对比Fig.5 Comparison of real density map and predicted density map of Part_A test picture

图6 Part_B测试图像的真实密度图与预测密度图对比Fig.6 Comparison of real density map and predicted density map of Part_B test picture

2.3.2 基于UCF_CC_50数据集的实验结果

在数据预处理阶段，将每张图像都随机裁剪成相同大小的16 份，并保证这16 份子图相加能够覆盖整张图像。在UCF_CC_50数据集上进行了训练与测试，结果如表3所示。

表3 不同算法在UCF_CC_50数据集上的MAE和MSE对比Tab.3 Comparison of MAE and MSE for different algorithms on UCF_CC_50 dataset

由表3 来看，LMCNN 模型在UCF_CC_50 数据集上的MAE 和MSE 比目前较好的算法GB-MSCNet 分别减小了10.1%和18.8%，模型性能显著提高，比基于CNN 结构的ACSPNet算法分别减小了20.3%和22.6%。该数据集人群密度较大，图像中由于视角失真引起的密度分布变化规律更为明显，充分发挥了LAFPNet 对局部高密度序列特征关联性的感知能力，充分说明LSTM 单元处理具有明显层次变化信息的图像的学习能力要比仅基于多尺度CNN 的效果更好。图7中展示了在UCF_CC_50 数据集上训练损失值的变化曲线，可以看出，大约在前1 000次的迭代中，损失震荡较为强烈，但总体趋势在降低，随着迭代轮数的增加，损失值最终收敛到了较低水平。对于回归任务来说，引进LSTM 单元能有效提高模型准确率。

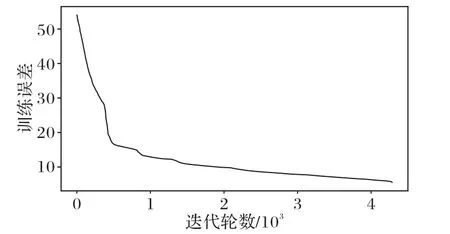
图7 UCF_CC_50数据集上的损失函数曲线Fig.7 Loss function curve on UCF_CC_50 dataset

3 结语

本文提出了融合全局特征感知网络与局部关联性特征感知网络的LMCNN人群计数模型，该模型以全局感知特征网络为主，基于多模融合策略引入LSTM 单元，利用LSTM 单元对序列的关联性特征具有强感知的特点，通过对空间维度特征与单图像内序列特征的充分融合，以减小由透视畸变和视角失真引起的人群计数误差，较为准确地预测密集区域人数。在Shanghaitech、UCF_CC_50 数据集上进行实验，结果表明LMCNN 网络在UCF_CC_50 数据集上对于高密度人群预测准确率均优于MCNN、ACSPNet 和GB-MSCNet，说明循环感知单元对于透视畸变、视角失真图像序列特征学习的充分性。但是当人群密度稀疏、背景杂乱时，LMCNN 模型预测能力较弱，主要由于人群个体尺寸变化规律的特征表示程度较小，导致循环感知特征时过多提取背景特征，空间维度上循环感知局部特征的学习能力无法得到很好的提升。在下一步工作中，将基于尺度和视角变化特征，进一步提高该模型在低密度人群图像中计数准确性。