统一计算设备架构下的F-X域预测滤波并行算法

杨先凤，贵红军*，傅春常

（1.西南石油大学计算机科学学院，成都 610500；2.西南民族大学计算机科学与技术学院，成都 610041）

（*通信作者电子邮箱gui18328655853@163.com）

0 引言

提高地震资料信噪比是进行高分辨率地震资料处理的关键，而恰当地去除随机噪声是提高地震资料信噪比的重要环节。目前在地震资料处理流程中，F-X 域预测滤波是去除随机噪声的有效方法。该方法由Canals Luis 于1984 年提出，经Gulunay［1］、HornBostel［2］等改进后逐渐投入生产使用。国内学者国九英等在文献［3］与文献［4］中分别提出了F-X 域预测与二维滤波并用以及F-X 域预测在三维场景下的使用，使F-X域预测技术进一步趋向成熟。

近年来，为了实现对地下复杂结构的精准勘探，地震资料随机噪声去除技术进一步向着高分辨率方向发展。主要有Oropeza 等［5］提出的多道奇异谱分析，以及Bekara 等［6］把F-X域经验模态分解应用于地震资料随机噪声的去除。以上两者处理非稳态信号的能力都强于F-X 域预测滤波技术，但计算复杂度更高。

随着现代探测设备与新兴处理技术的发展，地震资料处理精度已经能满足对地下复杂结构进行处理的需要，但是高分辨率技术往往意味着大量的计算时间。近十年来，统一计算设备架构（Compute Unified Device Architecture，CUDA）在高性能计算领域发展迅速，并且在地震资料处理领域中应用广泛［7-9］。在F-X域去噪领域，目前关于算法提速的研究较少，其中邴萍萍等［10］提出了改进的F-X 域经验模态分解技术及其分布式并行实现，但是并行的实现基于Matlab平台，在实际应用中具有的意义有限。本文在简述了F-X 预测滤波原理后，基于CUDA 模型对算法瓶颈进行分析，设计并实现了基于CUDA的并行加速方案。

1 F-X域预测去噪原理

F-X 预测滤波技术的基本原理是有效波在F-X 域是连续的、可预测的，而随机噪声是不相干的、不可预测的［11］。即当地震信号的每一个线性同相轴的所有频率分量都具有相同时差时，理论上其每一个频率分量在空间x方向上是可以预测的，通过信噪比高的频段求频率分量的预测算子，然后用对应的预测算子分别对x方向的复数序列进行预测滤波，从而压制随机噪声。

1.1 预测算子推导及求取方法

设震源子波为w(t)，道间时差为Δt，地震记录第一道反射记录为w(t-t1)（t1为第一道记录到达时间），经傅氏变换后为W(f)ei2πft1，对于某频率f0，沿空间x方向采样形成的复数序列为：

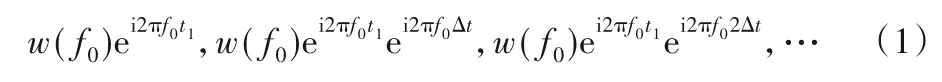
将式（1）转换为Z变换表示形式：

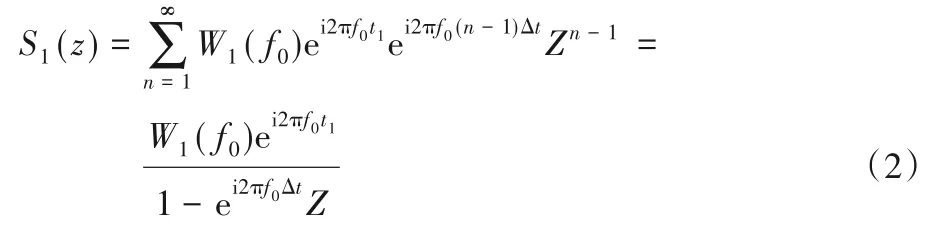
预测算子即ei2πf0Δt。一般地，对于剖面上m组不同时差的线性同相轴，其Z变换形式为：

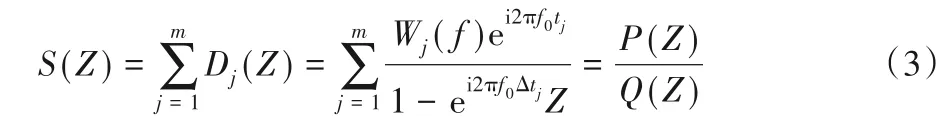
式中：Q(Z)为关于Z的m次多项式，Q(0)=1；P(Z)为关于Z的m-1次多项式。为了进一步说明，将式（3）写为：

当n≥m时，S(Z)Q(Z)中Zn的系数为0。若将Z视为一个预测误差滤波器的Z变换，用它对S（Z）的系数序列进行滤波，从输出的第m个点开始，其预测误差为0。即对于剖面上m组有不同时差的线性反射波同相轴，若预测算子长度L≥m，就可以将这些反射波预测出来。

然而在实际地震数据集中，并不能确定具有不同时差的线性同相轴的个数以及每组不同时差的信号的道间时差，因此F-X 预测滤波的预测算子由最小平方原理求取。设某一时间、空间窗口内地震记录数据为d(t，x)，变 换 到f⁃x域 为S(f，x)，对于某频率f0，令预测算子为g(f0，l)，其预测误差能量定义如下：

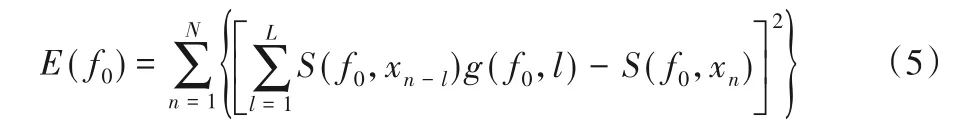
式中：n=1，2，…，N，N为地震道道数；l=1，2，…，L，L为预测算子长度。根据最小平方原理求解式（5）得到使E(f0)最小的g(f0，l)即对应频率的预测算子。

1.2 F-X域预测滤波流程

F-X 域预测滤波算法处理三维工区时，先进行傅氏变换将T-X 域数据转换到F-X 域，同时为提高数据读取效率，将数据由F-X 排列转变为X-F 排列，即将每个频率成分的数据按照空间位置顺序存储，如图1（a）所示；之后每次处理一个频率成分数据，处理过程分为两步，如图1（b）所示。

1）在Crossline方向取Windowsize×Inline大小窗口；

2）窗口内沿着Inline 方向每次取子窗口数据进行一次滤波。

图1（b）中算法对各个子窗口的计算是独立的，因此对算法并行优化时将各个子窗口的计算在GPU 上并行执行，利用GPU多核多线程的特点提升算法效率。

图1 F-X滤波流程Fig.1 Flowchart of F-X filtering

2 算法性能瓶颈分析

2.1 计算瓶颈

为分析算法的计算瓶颈，在本文4.1 节介绍的CPU 计算平台上，对采样点数量为1 001、大小为250 × 250 的工区进行测试，对算法的快速傅里叶变换（Fast Fourier Transform，FFT）、滤波、逆快速傅里叶变换（Inverse Fast Fourier Transform，IFFT）三部分进行耗时分析，结果如表1 所示。可以看出FFT与滤波部分是算法较为耗时的部分。算法逐道对地震数据作短时傅里叶变换（Short-Time Fourier Transform，STFT），处理的时窗长为150，循环取时窗进行计算的过程造成效率瓶颈。滤波部分以子窗口数据为处理单位，串行循环处理是算法执行效率的主要瓶颈所在。

表1 整体耗时分析Tab.1 Overall time consumption analysis

2.2 数据冗余读取

为方便说明，以原算法中参数为说明对象。如图1 所示，每次处理时，CPU 从硬盘读取一个频率切片的数据到内存。CPU 每次取20 × 20 邻域数据进行滤波，之后沿Inline 方向偏移17 道继续处理；Inline 方向一次处理完成后，沿Crossline 方向的偏移为17 道。此处存在两次数据冗余读取，以一个子窗口出发说明。第一处是在Inline方向上，相邻子窗口存在20 ×3 的数据冗余读取；第二处是在Crossline 方向上，相邻子窗口存在20 × 3的数据冗余读取。

3 并行优化策略

针对第2 章介绍的算法性能瓶颈，主要从两方面对算法进行效率优化：一方面是基于CUDA 对FFT 与滤波部分设计并行优化策略；另一方面是GPU 端基于共享内存与CUDA 流技术优化数据冗余读取。

3.1 FFT并行优化策略

本文算法对数据进行傅里叶变换时，以数据道为单位，每次取道上150 个数据，补零成256 个点进行一次傅里叶变换（如图2（a）），数据体较庞大时，这部分有大量的循环计算造成耗时，针对这种情况，利用并行FFT来提高效率。

对FFT进行并行化时，为发挥多线程计算优势，将一维数据排列成二维数据矩阵，在行方向、列方向各进行一次傅里叶变换。具体操作是将一个时窗的256 点排列为16 × 16 矩阵，Block 中64 个线程，16 个线程为一组完成一个时窗的傅里叶变换。先进行行方向变换，各个线程按编号从显存读取对应行的数据，此时的读取满足合并内存访问，不足的数据自动在线程内初始化为0，这样同时也优化了CPU 中补零过程的耗时，各线程完成处理后将数据存入共享内存；再进行列方向变换，读取对应列数据时进行合并线程访问，即线程束的线程访问相邻数据，且读取的开始位置是对齐的，则一组线程的读取会一次命中。本文数据是浮点型复数，每个数据占8 B，一行数据占128 B，本文显卡基于开普勒架构，支持32 B、64 B、128 B 三种缓存行模式，因此16 线程按相邻位置读取时满足合并线程访问，保证了数据读取效率。

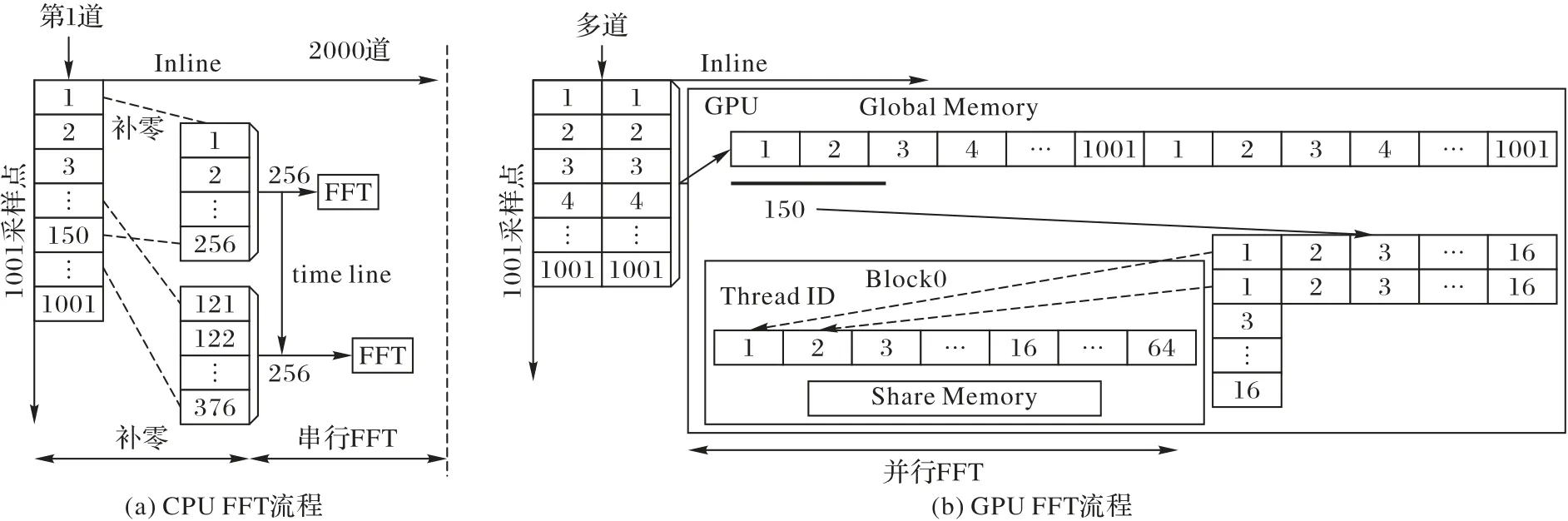
图2 FFT并行化流程Fig.2 FFT Parallel flow diagram

3.2 滤波部分并行优化策略

本文算法以20 × 20邻域数据为单位进行滤波，为方便说明，Inline、Crossline 方向分别称为x、y方向。对于每一个数据点，考虑其与x、y方向上邻近数据的相关性，线性预测算子演变为矩形预测算子。预测算子的求取［12］如下所示：

其中：R(t)、R(t+a)是地震记录的不同延迟时刻的自相关；h(t)为滤波因子。将式（6）表示成矩阵形式为：

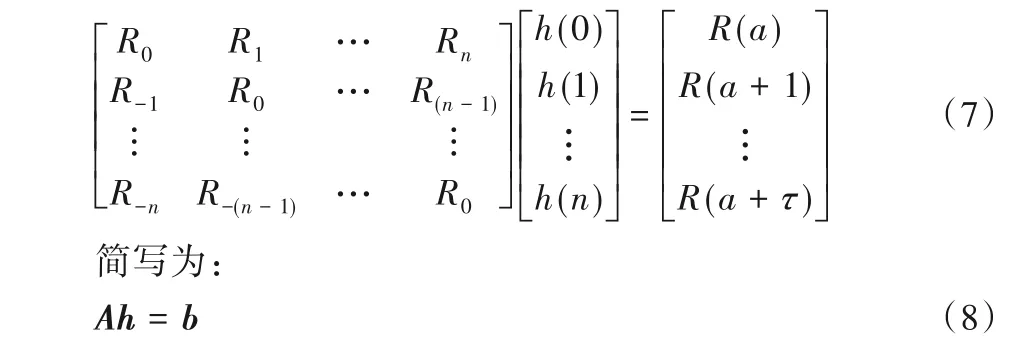
其中，A称为Toeplitz矩阵。

滤波过程分为求Toeplitz 矩阵A、求滤波因子、反褶积滤波三步，对滤波部分的并行设计由这三部分展开。

3.2.1 求Toeplitz矩阵并行优化策略

求矩阵A时，将数据每道做自相关运算并将不同时刻的值相加求和，就得到A的第一行，同时也不难得到其余n行。本文预测算子长度为7× 7，表示为h(-3：3，-3：3)，分别对应待预测值上下左右三邻域数据点权值。预测算子长度为49，由式（7），A列数为49，若以R(20，20)表示x方向上1～20个点，y方向上1～20 道每道做自相关的值之和，则矩阵A第一行对应 的 值 为R(20 -3：20+3，20 -3：20+3)，其 中，R(20 -3，20)表示数据矩阵沿着x方向左移三位对应邻域内各道做自相关运算的值求和。

进行并行优化时，将对应子窗口数据拷贝到Block共享内存中，64 个线程一组先进行矩阵A、b的计算，每个线程计算A第一行中对应时刻的值。由于数据矩阵在x、y方向移动时，中心14 × 14区域始终参与计算，本文先对这部分数据进行并行求和归约如图3，将20 × 20 数据处理成7× 7 数据后，各线程读取相应值完成A、b的计算。

图3 并行归约流程Fig.3 Flowchart of paralleling and reduction

3.2.2 求预测算子并行优化策略

已知A、b后，采用雅可比迭代根据式（7）对预测算子h进行求解。将式（7）每行改写为hi的表达式形式，记迭代次数为k，hik表示第k次迭代hi的值。hik值由下式计算：

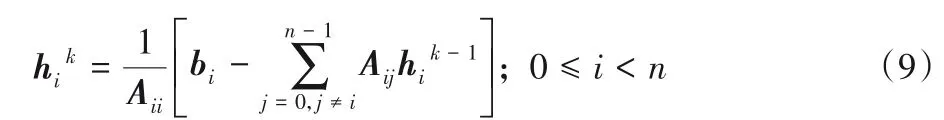
表示通过hik-1计算hik，不断迭代使hik趋近解。本文对雅可比迭代进行并行优化来提高计算效率，初始化hi0为0.01，收敛阈值ε为0.000 1，雅可比迭代的并行计算过程如图4所示。其中：Flag 是对所有线程可见的共享变量；hThreadIDk与hThreadIDk-1是线程中存储的对应下标两次迭代的值。每次更新h时，不同下标的hi互不影响，因此让一个线程进行式（7）中一个hi方程的迭代。Flag 初始化为false，若当前线程两次迭代值误差超过阈值，则置Flag为true，继续迭代。

3.2.3 反褶积滤波并行优化策略

反褶积滤波是预测算子与数据点逐点卷积的过程。预测算子为7× 7，数据矩阵为20 × 20，遍历数据矩阵每个值，以其为中心，取上下左右三邻域内7× 7 的数据（不足的数据为0）与预测算子卷积，结果表示当前值的滤波结果。

为了提高读写带宽，共享内存一般分成32块，即bank，一个bank 大小为4 B。线程对不同块以及同块同位置数据的访问不会产生冲突，但访问同块不同位置时会产生冲突，此时读取效率低下。对反褶积部分进行并行化时，数据矩阵存储在共享内存中，Block中线程读取对应区域数据进行一个数据的的卷积计算，此时20 × 20线程与20 × 20数据一一对应，由于线程对共享内存的数据访问重叠性较大，很容易发生Bank conflict。

为了减少Bank conflict对效率的影响，记编号在同一行的线程为一组，线程按行分为20 组。同一组的线程从同一起始位开始读取，不同行的线程组设置不同的起始位start，start 的取值为（0：21），此时20 组线程的读取起始位刚好在矩阵次对角线上，如图5，有16 组的读取不会产生Bank conflict，之后组号和为20 的线程交换起始位，这样各组线程则完成了一行数据的读取。之后各组上下移动三次，各个线程就完成了所需数据的读取。

图4 雅可比迭代流程Fig.4 Flowchart of Jacobi iteration

图5 数据矩阵读取示意图Fig.5 Schematic diagram of data matrix reading

3.3 冗余读取优化策略

解决数据冗余读取主要使用了CUDA 流。CUDA 模型中，CUDA 流表示GPU 的一个操作队列，在支持异步拷贝引擎的Tesla 显卡上，数据拷贝与计算可同时执行，某一条流的数据拷贝时间可以被其他流的计算时间掩盖，CUDA 流的应用价值已经得到验证［13-15］。将20个窗口求Toeplitz矩阵、求预测算子和反褶积滤波的过程视为一个计算任务，由一个流执行一个任务的数据拷贝与计算。对多个任务的计算采用流水线方式如图6，Stream2的数据拷贝与Stream1的数据计算相互重叠，因此可提高整体效率。

图6 冗余读取优化示意图Fig.6 Schematic diagram of redundant reading optimization

一个流中各个子窗口的计算相互独立，可再细分到Block中并行处理。为降低Inline 方向数据的冗余读取对效率的影响，将一个流中的8 个子窗口打包成一个数据段，由一个Block执行一个数据段的计算，利用共享内存提高子窗口间重叠数据的访问效率。若工区一条测线上数据道数为2 000，则一个流中有300个数据段，即需要申请300个Block进行计算。

4 实验结果分析

4.1 实验环境

本文实验采用的硬件配置：Inter Corei5-8300H，主频2.30 GHz；内存8 GB；NVIDIA Tesla K20c，显存为4 733 MB。软件环境：Windows 10（64 位）操作系统；VS2010 +QT 4.8.7+CUDA9.1 编程环境。测试数据为某工区叠后数据，具体参数如下：数据大小为30.9 GB，线号范围为1 120～1 370，共计88 801道，每道采样点数为1 001。

4.2 计算精度分析

图7 为1 130 测线在CPU 及GPU 平台上的计算剖面效果对比，无论从整体趋势还是细节来看，CPU 与GPU 平台计算结果基本一致。从两平台的计算结果误差图（c）可以看出，本文并行算法的误差绝对值达到10-9，能满足实际工程处理对于精度的要求。

4.3 效率对比

为了验证并行算法在性能上的提升情况，选取采样点均为1 001的不同工区，分别测试了优化冗余读取前后算法各部分在GPU 与CPU 平台上的计算时间，结果如表2 所示。从局部来看，FFT 过程有较多从硬盘拷贝数据的过程，这个过程会随着工区规模增加而明显影响程序的性能，因而FFT 部分的加速比增幅略低。求Toeplitz矩阵过程中，各线程访问共享内存时存在难以优化的Bank conflict，这是提高其优化效率的主要瓶颈。利用雅可比迭代求预测算子时，每次需要对各线程迭代结果进行同步，之后在单线程中进行收敛判断，这是算法流程的固有瓶颈。

从整体来看，算法效率随着数据规模的提升而提升。总体加速Ⅰ为优化冗余读取前算法整体在CPU/GPU 平台上的效率比较，由于CPU 处理部分的开销，算法效率提升了6.4～8.1 倍；总体加速Ⅱ为优化冗余读取后算法的效率对比情况，可以看出优化后并行算法效率是串行算法的8.9～11.9 倍，表明了这部分工作对本文算法的必要性。

5 结语

本文在NVIDIA GPU 平台上利用CUDA 并行编程语言，对F-X 域预测滤波算法进行并行优化使算法效率达到7.4～9.1的加速比；并在优化CPU/GPU 数据拷贝过程后，使算法效率进一步达到8.9～11.9 的加速比。本文算法还存在的瓶颈有两方面：一是数据在FFT 与滤波处理后生成的中间数据较大，需要存储在硬盘上而造成耗时；二是FFT后的数据转存为X-F 顺序数据时不满足合并内存访问，数据体较大时，这部分耗时也较大。