可验证的隐私保护k-means聚类方案

张 恩，李会敏，常 键

（1.河南师范大学计算机与信息工程学院，河南新乡 453007；2.智慧商务与物联网技术河南省工程实验室（河南师范大学），河南新乡 453007）

（*通信作者电子邮箱zhangenzdrj@163.com）

0 引言

聚类算法在机器学习、信息检索、模式识别等领域的数据挖掘中具有广泛的应用，在现实生活中，对医疗、社会科学、商业等应用的研究有着重要的作用。例如，现有两个医疗机构，每个机构都拥有患者的疾病和临床等治疗过程收集的数据集。假设这两家机构使用各自的方法收集数据后，希望将数据组合在一起进行训练，并确定使用聚类算法能够给疾病控制机制提供更好的研究方向。由于政策法规的约束以及数据的敏感性，双方均不愿意将数据共享，如何在保护隐私的前提下协作地在联合数据集上进行聚类成为一个具有挑战性的问题。

目前，大数据的存储和计算研究已趋近成熟，但是面临来自不同数据源的联合数据的隐私问题仍有待优化。在联合计算过程中，如果有一个可信的第三方，Alice和Bob都愿意将数据发送给该第三方，那么该第三方可以使用聚类算法训练双方的数据并将聚类中心发送给Alice和Bob。然而，在现实中，很难找到完全可信的第三方。针对此类问题，一系列文章结合安全多方计算［1-4］对聚类算法进行研究。

现有的保护隐私的聚类方法需要大量的计算、通信和存储开销，当训练大量数据时，如果用户没有足够的资源，就无法进行聚类。云外包计算的出现提供了很好的解决方法，云外包计算［5-6］的一个基本优势是数据外包的实现，使得用户在资源受限的设备上进行大量的数据存储和使用。通过云外包服务，企业或个人可以将大量复杂、耗时的计算和存储任务外包给不可信的云服务提供商（Cloud Service Provider，CSP），这样有利于分享资源、节约开销和降低创业成本。然而将数据外包到云服务器，剥夺了客户对其数据的直接控制权，不可避免带来一些新的问题。在将数据外包到服务器进行计算时，服务器为了节省计算资源，可能不经计算就返回错误结果。即使在半诚实模型中，服务器诚实的执行协议也会在计算过程中遭遇黑客、病毒攻击以及服务器故障等情况，导致返回错误结果。因此用户在接收到服务器返回的结果后，需要一种验证机制判断结果的正确性。现有云外包的隐私保护k-means聚类算法研究中尚不能解决验证结果正确性的问题。此外，在外包环境下，聚类的初始化算法对聚类结果和算法的迭代效率有很大影响，但是先前云外包方案中并未对聚类初始化进行研究。

针对以上问题，本文提出了一种基于云外包的可验证隐私保护k-means 算法方案，适用于训练任何分区的数据，目的是在不泄露各方隐私数据的情况下根据距离度量将相似的数据进行聚类，以及对云返回的结果进行验证。本文主要工作如下：

1）结合秘密共享、混淆电路等多种安全计算方法，提出了一种基于外包的k-means聚类隐私保护方案，在多用户的场景下将数据外包到两个非合谋的服务器，服务器对隐私数据进行k-means聚类，节省了用户的大量开销。

2）在多用户外包的条件下，提出了新的聚类初始化的方法。用户对自己的明文数据执行k-means 聚类算法，得到k个聚类中心，并将其拆分成子份额形式发送给服务器；服务器安全地求聚类的平均值，得到初始化后的聚类中心。此初始化方法可以有效提高算法的迭代效率。

3）在计算最小值算法中，建立一个数组记录份额值属于哪一个聚类中心，使得云服务器可单独地计算更新的聚类中心份额值，节省了部分开销和降低了时间复杂度。

4）首次提出了一种在隐私保护k-means 聚类算法云外包下的验证机制，能够有效验证云返回的聚类结果。当服务器返回聚类结果后，用户之间协作进行验证，从而判断服务器是否诚实遵循协议。

1 相关工作

随着数据挖掘的快速发展及应用，其数据带来的隐私问题越发受到关注。隐私保护数据挖掘最早由Agrawal 等［7］以及Lindell 等［8］于2000 年在不同的框架下提出，分别采用数据扰乱和安全多方计算方法对决策树进行隐私保护训练。在数据挖掘中，聚类作为统计数据分析的一种常用技术，应用于许多领域，以下主要讨论k-means聚类隐私保护的相关研究。

现有的保护隐私聚类算法在不同数据分布下进行研究，包括水平分区数据、垂直分区数据和任意分区数据。Vaidya等［9］最早对垂直分区数据设计k-means 算法的隐私保护方案，数据按属性分发到各个参与方，每个参与方仅对自己的属性数据学习；但是该协议需要三个非共谋参与者的存在，在实际应用中很难实现。Yi 等［10］在不泄露中间参数情况下完成聚类。Jha 等［11］提出了两种k-means 聚类隐私保护协议，将算法各步骤的聚类均值泄露给参与方，分别采用基于不经意多项式计算和基于同态加密实现，并且此方法仅适用于水平分区数据。Jagannathan 等［12］首次提出在任意分区数据上进行k-means聚类算法的隐私保护，通过两方合作将所有中间参数分割成随机的分区。Bunn 等［13］提出了一种基于同态加密的两方k-means聚类保护协议，在寻找最优聚类过程中不公开中间参数和聚类分配情况，但是扩展到多方k-means 聚类时，协议不能抵抗共谋攻击。Xing等［14］解决了用户和聚类算法服务提供者之间的合谋问题。Mohassel 等［15］通过1-out-of-N 不经意传输技术实现了高效的安全乘法。Meskine 等［16］综述了现有的基于安全多方计算的隐私保护k-means 聚类算法。Su等［17］从非交互角度提出了一种新的差分隐私k-means 聚类算法。Feldman 等［18］提出了一种差分隐私k-means 聚类，方案的误差与维数之间呈亚线性。Huang 等［19］提出一种优化差分隐私方法，通过Wasserstein距离减少差分隐私的误差值。

利用云外包可以有效节省用户的计算资源，将大量复杂、耗时的计算外包到云服务器。Rao 等［20］提出一种保护隐私的分布式聚类机制，通过将多用户数据外包到云服务器，利用同态加密算法设计k-means聚类方案；但是该方案不能抵抗合谋攻击。Liu 等［21］允许数据拥有者使用同态加密方案对数据加密，服务提供者对密文进行k-means 聚类，并使服务提供者可以将加密数据与数据提供的陷门信息进行比较；但是该方案只保护一方的隐私。Jiang 等［22］提出了两方外包的k-means 隐私保护方案，每一方的数据仅加密一次，但是在计算过程中用户和云交互次数多，且更新的聚类中心未保护。然而，以上云外包的方案均不能对云服务器返回的聚类结果进行有效验证，此外现有云外包方案初始化产生的集群中心随机性大，使得算法的迭代效率低。本文提出了一种验证算法，使得用户能有效验证云服务器返回的聚类结果，并且改进了初始化中心方法，能提高算法的迭代效率。

2 基础知识

2.1 k-means聚类

聚类在机器学习中属于无监督学习算法，给定一组数据，聚类算法根据数据的特征将数据点映射到不同的组，在同一组的数据具有相似的特征或属性，在不同组的数据应具有高度不相似的特征或属性。k-means 算法［23］为聚类应用最广泛的算法之一，以一种迭代循环的方式将一组数据分成k个聚类，其终止条件为聚类中心点之间的平方误差值准则最小。以下对k-means聚类算法作简单描述。

算法1k-means聚类算法。

输入n个数据点，确定聚类的数目k；

输出k个聚类中心μ={μ1，μ2，…，μk}。

1）初始化k个聚类中心：W={W1，W2，…，Wk}。

2）迭代开始，重复执行以下步骤。

3）计算每个数据点到k个聚类中心的距离，并将其分配到最近的聚类中心。

4）更新聚类中心：对每个聚类中心，计算属于此聚类中心所有数据点的平均值，作为新的聚类中心点。

5）判断是否达到终止条件：若满足条件，则返回新的聚类中心点；否则，继续执行3）、4）、5）。

2.2 加法秘密共享和乘法三元组

本文协议涉及的大部分数据是通过加法秘密共享技术［24］在两个参与方之间共享，下面简要回顾加法秘密共享的方案。

2.3 混淆电路

混淆电路是目前最常见的用于两方安全计算的通用技术。Yao［2］首次提出混淆电路，后来Ballaer等［25］给出了标准化定义。混淆电路技术的优化研究主要有point-and-permute［26］、free-XOR 门［27］和半门［28］。本文使用Ballaer 等［25］提出的混淆方案，首先简要地回顾此混淆方案，主要算法如下：

Gb：输入（1λ，f），其中，λ为安全参数，f为布尔电路；输出（F，e，d），其中，e为加密密钥，d为解密密钥，F为混淆电路。

En：输入（e，x），其中x∈{0，1}n，输出一个混淆输入值X。

Ev：输入（F，X），输出混淆输出值Y。

De：输入（d，Y），输出明文输出值y。

在两方安全计算中，Alice 和Bob 在不泄露各自隐私输入的情况下，计算函数并得到输出结果。Alice 将函数的布尔电路f转换成混淆电路F，并将自己的混淆输入发送给Bob。Bob在不泄漏输入数据的情况下从Alice 那得到混淆输入，并根据混淆电路计算出函数对应的混淆输出值。在计算过程中没有泄露有关输入的任何信息，得到两方计算的结果。本文使用两个简单的混淆电路构建安全协议：加法混淆电路和比较混淆电路。

2.4 半诚实模型

半诚实模型［29］下要求半诚实参与者或诚实参与者执行协议。诚实参与者完全按照协议的步骤执行，同时对协议中的输入、输出以及中间结果进行保密；半诚实参与者同样会按照协议的步骤执行，不会恶意修改数据，但是在协议的执行过程中，会收集其他参与者的信息，以在协议结束后推断其他参与者的输入信息或将其泄露给攻击者。

定义 令π表示隐私保护k-means 算法协议，F表示理想模型下的函数。如果对于现实模型下任何概率多项式敌手A，存在理想模型下的敌手S，使得协议π在现实和理想情况下计算不可区分，即满足

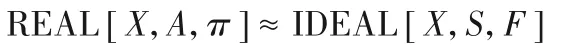
则证明协议π安全实现理想函数F。

3 构建模块

本章设计用于隐私保护k-means聚类算法的一些子模块，包括聚类初始化算法、安全欧几里得距离算法、安全计算最小值算法和验证算法。方案使用的部分符号见表1。

表1 符号定义Tab.1 Notations definition

3.1 聚类中心初始化

聚类中心的初始化方法包括很多种，找到一个合适的初始化聚类中心方法对聚类的结果至关重要，所以在不同的聚类条件下，需要采用不同的初始化方法。一种常见的方法是随机取k个聚类中心，在隐私保护环境下，让一个参与方随机产生k个聚类中心值，分成份额值发送到两个服务器，这种方法易于实现；另一种方法是在数据集中挑选k个不同的数据点的值作为聚类中心，此条件下的隐私保护也可简单地实现。但是，这两种方法产生的聚类中心随机性较强，会影响到k-means聚类的结果。

本文提出了一种新的适用于云外包情况下的初始化算法。首先每个参与方对各自的明文数据进行k-means聚类，得到k个聚类中心点，并将得到的值通过加法秘密共享技术分成两个子份额，分别发送给两个服务器；服务器接收到所有用户的份额值相应地求得对应份额值的平均值，理论上是对参与者产生的聚类中心求平均。具体初始化算法如算法2。

算法2 聚类中心初始化算法。

3）Sj(j∈{0，1})有m个聚类中心集合，并计算得到初始化后的聚类中心：

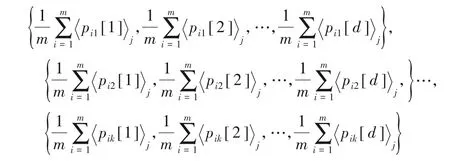
按照以上初始化算法得到的聚类中心比随机化生成的聚类中心在迭代次数上更具有优势。通过此初始化方法得到的聚类中心点能够有效减少算法的迭代次数，使得整个隐私保护环境下的k-means算法训练的复杂度降低。

3.2 安全的计算欧几里得距离

在机器学习中，欧几里得距离是k-means聚类算法中最常用的判断数据相似度的距离度量，计算距离的目的是对数据点计算得到的距离值进行比较。为了提高计算效率，将欧几里得距离改为欧几里得平方距离（Euclidean square distance，Esd），并不影响比较大小的结果。本文定义两点x、y之间的安全欧几里得平方距离计算公式为：z←FEsd(x，y)。

在欧几里得计算时，需要使用安全乘法技术，利用乘法三元组协助计算乘法，可将大量的计算操作放在离线阶段，在线阶段只进行少量的计算便可完成安全乘法操作。

的结果份额值。最终，S0、S1在不泄露各自输入数据的情况下，得到函数的结果份额值。

3.3 安全计算最小值算法

Qi(i∈{1，2，…，n}) 点到k个聚类中心的距离为{di1，di2，…，dik}，S0和S1分别持有数据和，需要考虑如何在不泄露各自份额值的情况下求出k个数据的最小值。采用混淆电路技术进行数值比较，可达到在不泄露任何输入数据的信息下得到输出结果。利用混淆电路的特点，设计了一个适合在秘密份额值的情况下比较大小的电路结构（Secure CoMPare circuit，SCMP），并调用此电路得到一组数据的最小值。最小值算法如算法3所示。

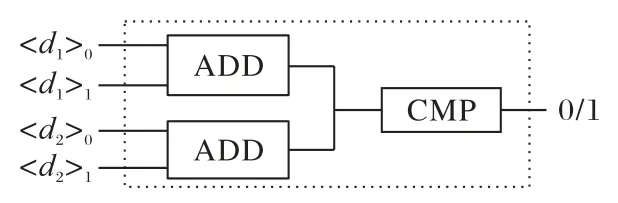
图1 SCMP电路图Fig.1 SCMP circuit diagram

通过SCMP 电路图实现两个数值在不泄露数据的情况下安全地比较大小，调用此结构k-1 次实现对k个值求得最小值，求最小值算法的复杂度为O(k)。

3.4 验证算法

在将数据外包到服务器后，一个安全问题是由不受信任的第三方服务提供者执行协议，其在计算过程中，为了节省计算资源，没有执行聚类算法直接返回错误结果，但是用户并不能确定服务器返回的结果是否正确。即使服务器诚实地执行协议，在计算过程中，可能遭受黑客攻击或者服务器出现故障，导致返回错误的结果。所以，用户需要对服务器返回的结果进行验证，验证的最终目标是验证服务器返回的聚类中心结果是否达到局部最优。

在验证阶段，用户之间协作计算，通过验证部分聚类点的准确性来判断服务器是否诚实地执行协议。例如，任意挑选两个聚类中心点，每个用户运行明文k-means 协议，得到属于此两个聚类的数据点，计算数据点的平均值并公开。现在每个用户接收到其他参与方的值，对接收到的所有值求平均，再计算与之前的两个聚类中心点之间的欧几里得距离，若结果小于不可忽略值，则证明服务器诚实的执行协议。具体计算如下：

算法4 验证算法。

在验证算法中，参与方协商对e个聚类中心点进行验证，有效地验证服务器返回的结果是否达到局部最优，以此判断服务器是否诚实地执行协议。

4 基于外包的多方k-means隐私保护方案

本文提出了一个可验证的隐私保护k-means 聚类算法方案，整体框架如图2 所示。首先，用户在本地计算初始化聚类中心和乘法三元组，将其与用户数据以份额值的形式发送到两个云服务器；然后，服务器在隐私数据下进行k-means 聚类算法Lloyd迭代，最终得到训练好的聚类中心，并发送给用户；最终，用户使用算法4 对结果进行验证。将协议分为两个阶段：离线阶段和在线阶段。

图2 可验证的隐私保护k-means聚类方案框架Fig.2 Framework of verifiable privacy-preserving k-means clustering scheme

4.1 离线阶段

在离线阶段需要处理k-means算法训练的数据集，以及用于算法训练过程的辅助参数。假设存在两个非合谋的服务器S0和S1，m个用户{U1，U2，…，Um}，Ui持有的数据为ai(i∈{1，2，…，m)}个。m个用户总的数据为n个，且满足a1+a2+…+am=n，组成的联合数据为{Q1，Q2，…，Qn}。为了实现对多个用户的联合数据做分类处理，每个参与方通过加法秘密共享技术将隐私数据分发到两个服务器：服务器S0持有的隐私数据为；服务器S1持有的隐私数据为

为了在线阶段的运算，在离线阶段需要生成一些辅助参数，产生大量的乘法三元组来协助在线阶段计算安全乘法。

4.2 在线阶段

在线阶段调用第3 章的算法完成隐私k-means 聚类算法的训练。具体情况如下：

4.2.1 聚类初始化

初始聚类中心对聚类的结果有较大的影响，合适的初始化聚类中心在聚类算法中起到关键作用。调用第3 章的初始化算法2得到初始化聚类中心点并记为：

4.2.2 Lloyd’s迭代

执行以下步骤，直到满足终止条件，停止迭代。

1）安全欧几里得平方距离。

迭代的第一步为计算每个点到每个聚类中心之间欧几里得平方距离，调用第3 章的函数FEsd。对于i∈{1，2，…，n}，h∈{1，2，…，k}，S0和S1合作计算欧几里得平方距离份额值为，最终每个数据点Qi得到的距离向量为(i={1，2，…，n})。

2）分配点到聚类中心。

迭代第2 步需要将每个点分配到对应的聚类中心，在计算完每个点Qi到k个聚类中心值的距离份额值后，需要计算Qi点到k个聚类中心的距离最小值，并将此点分配给该类。定义一个大小为n的数组D并初始化为0。对于第i（1 ≤i≤n）个数据点Qi，S0和S1各自输入k个距离份额值，并调用最小值算法3 计算得到的结果g，使得D[i]=g，表示把第i个数据点分配到第g个聚类中心点。将数据集Q={Q1，Q2，…，Qn}每个点构成的距离向量Vi（1 ≤i≤n）按上述方法进行分类，最终数组D存放每点的分类情况，以此达到分配点到各个聚类中心的目的。

3）更新聚类中心。

迭代第3 步更新聚类中心，从上述步骤中，得到一个数组D[n]，根据D[n]的值，S0和S1分别求出新的聚类中心。Si设置两个数组Hi［k］和Li［k］，将数组初始化为0，Hi［k］保存每个聚类的所有数据份额值的和，Li［k］保存每个聚类的数据个数，i=｛0，1｝。对于j∈{1，2，…，n}，Si计算Hi[D[j]]=和Li[D[j]]=Li[D[j]]+1。对 于h∈{1，2，…，k}，Si计 算最终

4）检查终止条件。

S0和S1分别输入新的聚类中心的秘密份额值和以前的聚类中心点的秘密份额值，并调用欧几里得平方距离算法，计算得到为新旧聚类中心的相似度。定义φ为一个不可忽略值，将其作为算法的终止条件：若τ＜φ，停止算法的执行，将新的聚类中心份额值发送给各个参与方；若τ＞φ，继续迭代。

4.2.3 验证算法

每个用户Ui(i∈{1，2，…，m})接收到服务器返回的聚类结果份额值后，调用重构算法得到聚类结果{ζ1，ζ2，…，ζk}；再调用第3 章的验证算法对服务器返回的结果进行验证，每个用户执行验证算法得到的聚类中心和服务器返回的聚类中心之间的欧几里得距离为，说明服务器诚实的执行协议，否则服务器存在欺骗或遭受黑客病毒攻击。

5 安全分析

本文提出的多方外包的k-means 聚类隐私保护协议在满足以下定理时，达到在半诚实模型下是安全的。

定理如果初始化算法、安全欧几里得算法FEsd、安全最小值算法、终止条件算法和验证算法在半诚实模型下是安全的，则k-means聚类隐私保护协议在半诚实模型下是安全的。

为了证明上述定理，首先给出初始化算法、安全欧几里得算法FEsd、安全最小值算法、终止条件算法和验证算法的安全证明，然后根据组合定理［29］说明整个k-means协议为安全的。

假设有m个参与方C={U1，U2，…，Um}，和两个服务器S0和S1且服务器不能合谋。

证明 假设存在一个半诚实敌手A，腐败用户的任何子集和最多腐败一个服务器，敌手只能学习到已腐败用户的数据和输出，而学习不到诚实用户的数据。协议考虑存在一个敌手A腐败了S0以及除了用户Ui之外的所有用户I，I为用户集合C的子集，i∈{1，2，…，m}。腐败S1的情况和S0类似，证明中不再详细阐述。有一个模拟器S黑盒调用敌手A。

1）初始化算法的安全证明。构建一个模拟器S，模拟器调用敌手A腐败服务器S0和用户集合I，并模拟其在协议执行过程中的操作。在对用户隐私数据处理时，模拟器S模拟诚实用户Ui发送随机份额值给敌手A。在初始化聚类中心时，敌手A产生k个随机份额值发送模拟器S。S模拟诚实参与方S1运行初始化算法得到初始化聚类中心为根据秘密共享产生份额值的随机性，模拟器S对得到的初始化聚类中心份额值具有不可区分性。

2）安全欧几里得算法的安全证明。在计算欧几里得距离时，模拟器S模拟诚实方S1与腐败方S0交互计算模拟器S模拟诚实方利用三元组计算一些参数发送给敌手A，同样敌手A产生随机值发送给模拟器，模拟器S和敌手A得到的份额值。最终得到一组距离向量n}，j∈{1，2，…，k})。根据秘密共享的安全性和初始化过程产生的值为随机的，模拟器和敌手A无法得知诚实用户的隐私信息，所以在理想模型中，模拟器S计算的结果和现实世界运行同样的协议输出的结果具有不可区分性。

3）安全最小值算法的安全证明。在分配数据到最近的聚类中心时，模拟器S模拟诚实参与方S1和腐败参与方S0交互比较数据的大小，在调用SCMP 比较电路时，模拟器S模拟诚实参与方产生混淆电路发送给敌手A，敌手A计算混淆电路的结果发送给模拟器S。交互实现最小值函数，得到距离向量的最小值索引值并将其赋值给D［i］。根据混淆电路的安全性，敌手A和模拟器S无法得到诚实参与方的隐私输入，所以理想和现实模型下执行协议输出的结果具有不可区分性。

4）终止条件算法的安全证明。在检查是否达到终止条件时，模拟器S模拟诚实参与方和腐败参与方交互执行安全欧几里得距离，比较τ和φ，若τ＜φ，模拟器S将发送给敌手A。根据秘密共享的安全性，模拟器S和敌手A无法得到诚实参与方的输入信息，所以现实和理想模型中运行此算法具有不可区分性。

5）验证算法的安全性。在验证时，模拟器S模拟诚实用户Ui计算发送给敌手A，敌手A产生与相同数据格式的随机数发送给模拟器S，模拟器S和敌手A判断，来说明验证服务器是否诚实执行协议。在验证服务器返回的结果是否正确时，用户提供的是部分点的平均值，没有泄露数据的任何信息。

综上所述，提出的k-means隐私保护协议满足在理想和现实中不可区分性，在半诚实模型下是安全的。

6 实验与理论分析

6.1 功能比较

表1 是本文方案与文献［10，14-15，20-22］中方案的功能比较。文献［10，14-15］中提出的方案是用户数据之间相互合作训练隐私数据。文献［15］方案适用于任意分区的数据训练模型，文献［14］方案是针对水平分区数据设计的方案，这两个方案都保护了用户的数据以及聚类中心；文献［10］中提出的垂直分区数据的k-means隐私保护方案没有保护聚类中心值。以上方案都是在用户客户端完成隐私保护训练的。文献［20-22］中的这三个方案都是将数据外包后进行k-means 隐私训练，采用的都是同态加密方法，文献［20-21］方案在密文比较上通过添加保序索引实现，文献［21-22］方案在训练过程中会泄露聚类中心。本文方案采用秘密共享的技术将数据外包，相较其他方案在对隐私数据处理的问题上节省了用户的计算资源，并在任意分区数据上进行训练，在保护用户隐私数据的前提下能实现对聚类中心的保护。

针对以上外包方案没有验证服务器返回结果的正确性，提出了一种验证机制，通过用户之间协作计算部分聚类中心值，验证服务器是否诚实地执行协议。

从表2 中可以直观看出，本文k-means 隐私保护方案在多用户环境下对任意分区的数据实现了保护用户数据和聚类中心，并验证结果的功能。

表2 不同方案的功能比较Tab.2 Function comparison of different schemes

6.2 性能比较

在隐私保护环境下训练k-means 算法的时间主要分为用户时间、通信时间和服务器时间。通过计算本文方案和文献［20-22］方案的时间复杂度来研究方案的性能。其中：文献［20］是2015 年提出的多方外包k-means 算法的隐私保护方案，文献［21］是2014 年提出单用户下外包k-means 算法的隐私保护方案，文献［22］是2020 年提出的两方外包k-means 算法的隐私保护方案。

根据不同方案中出现的算法，从加密、计算欧几里得平方距离、计算最小值、更新聚类中心时的除法操作四个方面的时间复杂度分析，计算结果见表3。其中，n表示数据点的总数，d表示数据点的维数，k表示数据的分类个数，α表示距离值的二进制位数，m表示更新中心聚类点值的二进制位数。从比较结果中看出，协议在加密和欧几里得平方距离两个环节的计算时间复杂度保持不变的情况下，在求最小值和更新聚类中心时的除法操作环节时间复杂度明显降低。

表3 时间复杂度比较Tab.3 Time complexity comparison

通信复杂度是指在训练k-means 算法时用户和云服务器之间的通信。文献［21］中提出的方案单用户和云之间在每轮迭代时需要交互一次；文献［22］中提出的方案两方用户和云之间进行O（n*k）轮交互；文献［20］中提出的方案用户和云之间进行O（k*l）轮交互；而本文方案在将数据外包之后，用户不再参与k-means 算法的计算，直到返回满足条件的聚类中心，用户和云之间仅进行O（1）轮交互，因此本文方案的通信复杂度较低。

6.3 结果分析

本文算法的主要功能是两个云服务器安全有效地训练隐私k-means 聚类算法。实验主要研究算法的运行时间和运行效率以及隐私保护聚类算法的准确率。实验中计算机配置如下：操作系统为Linux，CPU 为2.3 GHz，内存为2.00 GB，结合Obliv-c库，利用C++进行开发。

本文实验选取2 个不同大小的数据集进行实验。第一个数据集S1［30］是研究聚类方案的基准，本文选取500 个二维数据，聚类个数为8；第二个数据集为人工合成（Synthetic）二维数据，数据集大小为100，聚类点个数为｛2，5｝。表4为数据集的简要描述。

表4 实验中使用的数据集Tab.4 Datasets used in the experiment

首先对Synthetic 数据集进行实验，分别在不同迭代次数和不同聚类个数的情况下运行。实验中将迭代次数设置为1、5、10，将聚类个数设置为2 或4。在安全k-means 聚类训练时S1和S2的运行时间见表5，其中：n为数据点的个数，k为聚类的个数，T为迭代次数。表5 表明，随着聚类迭代次数和聚类个数的增加，S1和S2的运行时间成倍地增加。当n=100，k=4时，在迭代次数为10时运行时间大约2 min。

对两个数据集进行隐私k-means 聚类，误差值φ=10-5，结果见表6。Synthetic 数据集需要迭代10 次达到收敛，总运行时间大约178 s；S1 数据集需要迭代7 次达到收敛，总运行时间大约481 s。

本文对得到的聚类结果进行准确性分析。准确度是评估聚类数据集正确分类的百分比。在本文中，使用本文提出的隐私k-means聚类和明文k-means聚类算法比较来产生模型的准确性。通过实验，Synthetic 数据集准确度达到97%，S1数据集准确度达到93%。S1数据集的明文k-means 聚类数据点和聚类中心分布图见图3（a），S1数据集的隐私训练k-means聚类的数据点和聚类中心分布图见图3（b）。通过本次实验表明，可验证隐私训练k-means 聚类准确度较高，具有较好的实用性。

表5 隐私保护聚类协议在Synthetic数据集上的运行时间单位：sTab.5 Running time of privacy-preserving clustering protocol on Synthetic dataset unit：s

表6 隐私保护k-means聚类在不同数据集的收敛时间和收敛时的迭代次数对比Tab.6 Comparison of convergence time and iterations when convergence by privacy-preserving k-means clustering on different datasets

图3 S1数据集的明文和隐私的k-means聚类Fig.3 Plaintext and privacy k-means clustering of S1 dataset

7 结语

针对现有方案未对云服务器返回的聚类结果进行验证的问题，本文提出了一种基于外包环境的多用户隐私保护的可验证k-means聚类协议。因为大部分计算在云上进行，任何计算能力较弱的参与方都可以运行协议实现保护隐私的k-means聚类。首先设计改进的初始化算法，有效提高算法迭代效率；同时利用乘法三元组实现安全乘法，并提出安全的求最小值结构，以及在更新聚类中心时，直接本地计算，不需要复杂的密文除法操作；并且，本文还提出了一种验证算法，当云服务器不经计算返回错误结果时，该算法使用户能验证部分聚类中心的正确性。在整个训练过程中，算法没有泄露用户的隐私信息。本文未考虑输出隐私的问题，但是其对k-means隐私保护同样重要，将作为下一步研究方向。